Lp-тен Lq-ға Урысон интегралдық операторларының шектеулілік, үзіліссіздік және компакттілік критерийлері


Мазмұны
- Lpкеңістігі және сызықтық операторлар . . . 3
- Сызықтық емес Урысон интегралдық
операторының кейбір қасиеттері . . . 10
- Урысон операторының бір классының
үзіліссіздік критерийлері . . . 16
- Әдебиет . . . 23
L p кеңістігі және сызықтық операторлар
1-анықтама.
f
(x) өлшемді функциясы жоғарғыдай біз функциялардың шектелуін кейбір берілген [a, b] сегментінде р-дәрежелі қосындыланатын деп аталады. Мұндағы p
 1, егер
1, егер
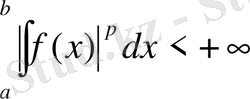 .
.
Мұндай функциялар жиыны L p арқылы белгілеу қабылданған (немесе L p [a, b] арқылы) . L 1 =L екені айқын.
1-теорема.
f
(x) функциясы, р>1 дәрежелі қосындыланатын яғни L
p
 L қосындыланады.
L қосындыланады.
Расында да егер E=[a, b], A=E(
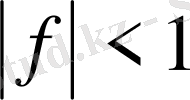 ), B=E-A болса, онда
f
(x) -функциясының қосындыланатын А-жиынында айқын, ал оның В-жиынында қосындылатыны мына жиынынан
), B=E-A болса, онда
f
(x) -функциясының қосындыланатын А-жиынында айқын, ал оның В-жиынында қосындылатыны мына жиынынан
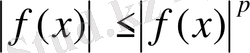 шығады. 2 - теорема осы сияқты дәлелденеді.
шығады. 2 - теорема осы сияқты дәлелденеді.
2-теорема. L p -ға кіретін екі функцияның қосындысы да осы класқа кіреді.
Шынында да, f (x) және g(x) L p -ға кіреді делік.
E=[a, b], A=E
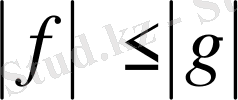 , B=E-A десек, онда
, B=E-A десек, онда
 үшін шығатыны:
үшін шығатыны:
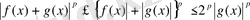 ,
,
бұдан
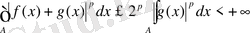
екендігі шығады.
Осылайша біз
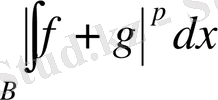 шекті интегралданатынына көз жеткіземіз.
f
(x) функиясымен бірге кез келген
k f
(x) - функциясы да L
p
-ға кіреді.
шекті интегралданатынына көз жеткіземіз.
f
(x) функиясымен бірге кез келген
k f
(x) - функциясы да L
p
-ға кіреді.
Мұндағы k - шекті тұрақтылық.
р>1 болсын.
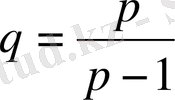 саны р-ға түйіндес көрсеткіш деп аталады.
саны р-ға түйіндес көрсеткіш деп аталады.
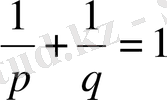
болаиыны себепті q-ға түйіндес көрсеткіш р бар, демек бұл р және q өзара түйіндес көрсеткіштер. Дербес жағдайда, егер р=2, онда q=2, яғни 2 өзіне түйіндес.
3-теорема.
Егер
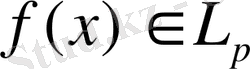 , ал
, ал
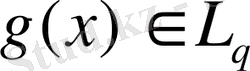 , мұндағы р және q өзара түйіндес, онда
f
(x) g(x) көбейтіндісі қосындыланады және
, мұндағы р және q өзара түйіндес, онда
f
(x) g(x) көбейтіндісі қосындыланады және
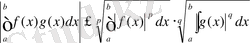 (1)
(1)
теңсіздігі дұрыс.
Дәлелдеуі: 0<α<1 болсын.
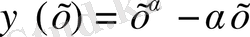 (0<x<+
(0<x<+
 )
)
функциясын қарастырайық.
Оның туындысы
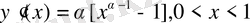 болғанда оң, ал x>1 болғанда теріс. Олай болса x=1-де
болғанда оң, ал x>1 болғанда теріс. Олай болса x=1-де
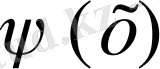 функциясының ең үлкен мәнге жетеді. Осылайша
функциясының ең үлкен мәнге жетеді. Осылайша
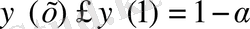 , бұдан шығатыны барлық x>0 мәнінде
, бұдан шығатыны барлық x>0 мәнінде
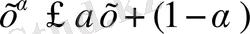 (2)
(2)
шығады.
А және В екі оң сан болсын. Егер (2) -ге x=A/B орнына қойып және алынған теңсіздікті В-ға көбейткеннен шығатыны
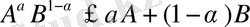 .
.
Теореманың шарттында айтылғандай, p және q - екі өзара түйіндес көрсеткіштер болсын. Егер
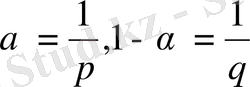 болса, онда бізде
болса, онда бізде
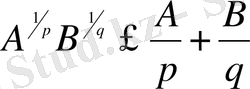 (3)
(3)
шығады.
Бұл теңсіздіктер A>0 және B>0 үшін дәлелденген. Осы сандардың біреуі (немесе екеуі) 0-ге айналса, ол теңсіздік әр уақытта дұрыс орындалады.
Осыдан кейін теоремада айтылғандай f (x) және g(x) функцияларын қарастырамыз.
Егер бұлардың ішінен тек біреуі нөлге эквивалентті болса, онда теореманың барлық тұжырымдары орынды. Бұл ерекше жағдайды есептемей, екі интегралды
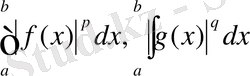
қатал оң деп тұжырымдап, мына функцияларды аламыз:
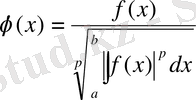 ,
,
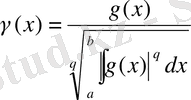 .
.
Егер (3) - ке апарып
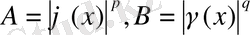 қойсақ, одан шығатыны
қойсақ, одан шығатыны
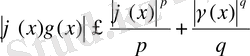 , (4)
, (4)
бұдан f (x) γ(x) көбейтіндінің қосындылануы, ал мұнымен бірге f (x) g(x) көбейтіндісі шығады.
Сонымен қатар
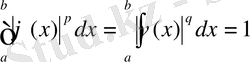
екенін ескеріп және (4) -ті интегралдап,
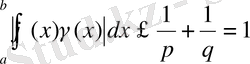 ,
,
табамыз, бұдан (1) - ден күштірек
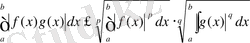 ,
,
L(1) теңсіздігі Гëлдер теңсіздігі делініп, p=2 болғанда Буняковский теңсіздігінің жалпылауы деп аталынады.
4-теорема.
Егер
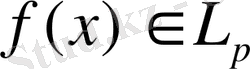 және
және
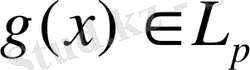 (
(
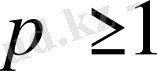 ), онда
), онда
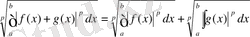 (5)
(5)
Дәлелдеуі: Теоремада p=1 екені айқын. p>1 және q p-ға түйіндес көрсеткіш болсын.
Теоремадағы
f
(x) +
g
(x) екі қосынды L
p
- да жатады, себебі
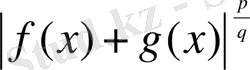 L
p
- да жатады.
L
p
- да жатады.
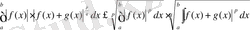 (6)
(6)
береді. Осы сияқты
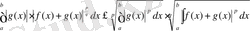 . (7)
. (7)
Бірақ
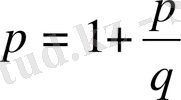 . Демек
. Демек
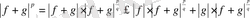 .
.
(6) және (7) - ден шығатыны
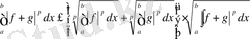 ,
,
ал бұдан келіп теорема шығады. [
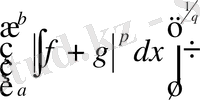 - ға қысқартылуы заңды, егер бұл теорема нөлден өзгеше болса, бірақ кері жағдайда теорема айқын] .
- ға қысқартылуы заңды, егер бұл теорема нөлден өзгеше болса, бірақ кері жағдайда теорема айқын] .
(5) -і теңсіздігі Минковский теңсіздігі деп аталады. p=2 болғанда бұл бізге белгілі. Коши теңсіздігіне айналады.
Бұл пайымдаумен Гëлдер мен Минковскийдің теңсіздігі анықталады:
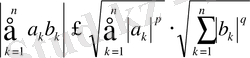
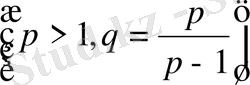 , (8)
, (8)
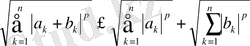
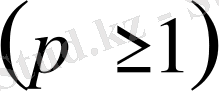 . (9)
. (9)
2-анықтама.
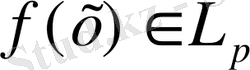 болсын.
болсын.
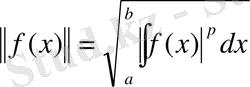
саны f (x) функциясының нормасы (L p - ның элементі сияқты) деп аталады.
Норманың келесі қасиеттері айқын:
І.
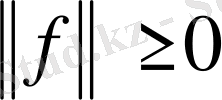 және
және
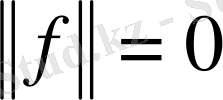 сонда тек қана сонда
сонда тек қана сонда
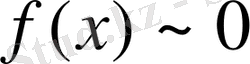
ІІ.
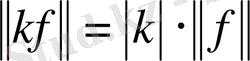 және дербес жағдайда
және дербес жағдайда
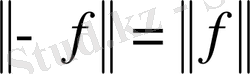
ІІІ.
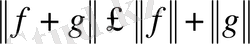 .
.
Норманың кіріспесі L p және L 2 үшін де геометриялық терминологияны орындауға болатынын көрсетеді.
Элементтердің жүйелі жинақтылығы
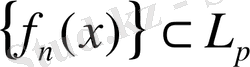 - ден
- ден
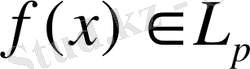 шегіне норма бойынша
шегіне норма бойынша
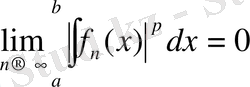 .
.
Жинақтылықтың бұл түрін орташа ретті жинақтылық деп атайды. Осылайша L 2 үшін де жинақтылықтың кейбір жүйесінен р орташа ретті өлшем бойынша жинақтылық шығады. Осылайша L 2 үшін шектің жалғыздығы және норманың өзара эквивалентті функциялығы шығады. Сонымен қатар L 2 сияқты L р элементтінің жүйелілігімен өзіне жинақталу түсінігі енгізіледі және дәлелденеді (L р кеңістігінің толықтығы) .
Бұл жерде біз жаңа идеялық моменттің болмағаны себепті сөйлемнің дәлелдеуіне тоқталмаймыз. Тура осылайша біз дәлелдеусіз §2 - гі 6-теоремадағы (соңғы b-a=2π) M, C, P, S және T кластарының әрбіреуі L р - ға барлық жерде тығыз.
Жинақтылықтың әлсіз түсінігі p>1 болғанда былай болады:
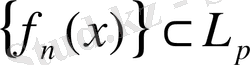 жүйелілігі
жүйелілігі
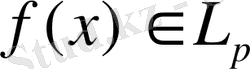 - ға әлсіз жинақталады, егер теңсіздік
- ға әлсіз жинақталады, егер теңсіздік
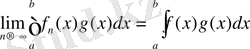 (10)
(10)
L p - дағы g(x) - функциясының кез келген орнын алатын болса, мұндағы q p - ға түйіндес көрсеткіш.
Гëлдер теңсіздігін пайдалана отырып орташа жинақталу жүйелілігінің (сол шекке) әлсіз жинақталатынын көрсете аламыз.
Егер p=1 болса, түйіндес көрсеткіш болмайды. Мұндай жағдайда
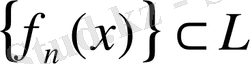 жүйелілігі, егер (10) теңсіздігі функцияның орнын алатын болса,
жүйелілігі, егер (10) теңсіздігі функцияның орнын алатын болса,
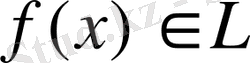 - ге әлсіз жинақталады.
- ге әлсіз жинақталады.
Қорытындылай келе талдауда
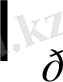 кеңістігінде қолданылатын (мұндағы
кеңістігінде қолданылатын (мұндағы
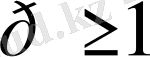 ) тағы бір типтегі «кеңістікті» келтірейік.
) тағы бір типтегі «кеңістікті» келтірейік.
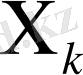 нақты санының L
p
кеңістігінде жиынның барлық жүйелілігін x=(x
1
, x
2
, x
3
, …) түсінеді.
нақты санының L
p
кеңістігінде жиынның барлық жүйелілігін x=(x
1
, x
2
, x
3
, …) түсінеді.
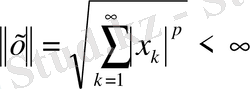
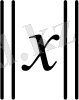 саны
саны
 элементінің нормасы деп аталынады. Жоғарыда айтылғандай
элементінің нормасы деп аталынады. Жоғарыда айтылғандай
 үшін L
p
элементі енгізіледі. k
x
- көбейтіндісі k сан, ал
үшін L
p
элементі енгізіледі. k
x
- көбейтіндісі k сан, ал
 элементі.
элементі.
Норма енді әдеттегі қасиетке ие.
І.
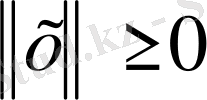 және
және
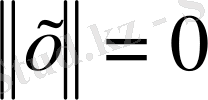 сонда тек қана сонда x=0.
сонда тек қана сонда x=0.
ІІ.
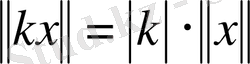 Equation. 3 және дербес жағдайда
Equation. 3 және дербес жағдайда
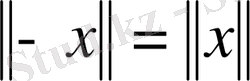 .
.
ІІІ.
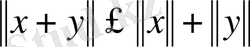 .
.
Алғашқы екі қасиет айқын, ал үшінші (9) - дан шығады. Норманың түсінігін пайдалана отырып өзіне жинақталу жиынында,
 барлық жерде тығыз
барлық жерде тығыз
 элементінің жүйелілігінің шектік түсінігі келіп шығады.
элементінің жүйелілігінің шектік түсінігі келіп шығады.
 элементінің жүйелілік шегі жалғыз ба, норма үзіліссіз бе,
элементінің жүйелілік шегі жалғыз ба, норма үзіліссіз бе,
 - кеңістігі толықтық қасиетіне ие бола ма бұған біз тоқталмаймыз.
- кеңістігі толықтық қасиетіне ие бола ма бұған біз тоқталмаймыз.
Е және Е 1 - екі сызықтық топологиялық кеңістік болсын.
Сызықтық операторда Е
 Е
1
деп
Е
1
деп
y= Ax,
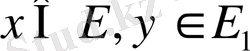 Equation. 3
Equation. 3
шартты қанағаттандыратын
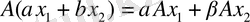 айтады.
айтады.
D
A
жиынтығы
 А - бейнелеуі үшін анықталып, А операторының анықталу облысы деп айтады. Жалпы айтқанда D
A
=Е деп ұйғарылмайтын, бірақ біз оны әрқашан да D
A
сызықтық көпбейне деп есептеп, яғни егер
А - бейнелеуі үшін анықталып, А операторының анықталу облысы деп айтады. Жалпы айтқанда D
A
=Е деп ұйғарылмайтын, бірақ біз оны әрқашан да D
A
сызықтық көпбейне деп есептеп, яғни егер
 , онда барлық
, онда барлық
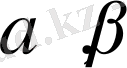 үшін
үшін
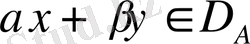 .
.
А операторы
 нүктесінде үзіліссіз болады, егер
нүктесінде үзіліссіз болады, егер
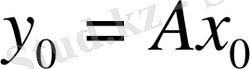 нүктесінің кез келген V маңайында х
0
- нүктесінде U маңайы бар болып, Ах
нүктесінің кез келген V маңайында х
0
- нүктесінде U маңайы бар болып, Ах
 N болса, онда х
N болса, онда х
 U
U
 D
A
. А операторы үзіліссіз D
A
жиынында егер ол әрбір
D
A
. А операторы үзіліссіз D
A
жиынында егер ол әрбір
 нүктеде үзіліссіз болса.
нүктеде үзіліссіз болса.
Е және Е
1
нормалданған кеңістік болғанда мына анықтама келесіге пара - пар. А операторы үзіліссіз деп аталады, егер кез келген
 үшін
үшін
 бар болса, мына теңсіздіктен
бар болса, мына теңсіздіктен
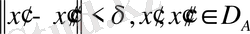
бұдан шығатыны
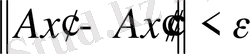
 жиыны Ах=0 үшін А сызықтық операторын ядросы деп аталады,
KerA
деп белгіленеді.
жиыны Ах=0 үшін А сызықтық операторын ядросы деп аталады,
KerA
деп белгіленеді.
 жиыны А сызықтық оператордың бейнесі деп аталып,
ImA
деп белгіленеді. Ядро сияқты, сызықтық оператордың бейнесі де сызықтық көпбейнелік болып саналады. Егер оператор үзіліссіз және D
A
=E онда
KerA
ішкі кеңістік, яғни тұйық. Сызықтық үзіліссіз оператордың бейнесі Е
1
-дің ішкі кеңістігі болу міндетті емес, тіпті егер D
A
=E.
жиыны А сызықтық оператордың бейнесі деп аталып,
ImA
деп белгіленеді. Ядро сияқты, сызықтық оператордың бейнесі де сызықтық көпбейнелік болып саналады. Егер оператор үзіліссіз және D
A
=E онда
KerA
ішкі кеңістік, яғни тұйық. Сызықтық үзіліссіз оператордың бейнесі Е
1
-дің ішкі кеңістігі болу міндетті емес, тіпті егер D
A
=E.
Бұл тараудың басында келтірілген сызықтық функционал ұғымы ол сызықтық операторының дербес жағдайы. Тіптен сызықтық функционал - бұл сандық түзуін берілген Е кеңістігіне аударатын сызықтық оператор. Оператордың сызықтық және үзіліссіздік анықтамасы жоғарыда келтірілген функционалдар анықтамасына сәйкесінше Е 1 =R болады.
Сызықтық емес Урысон интегралдық операторының кейбір қасиеттері
G
және
F
- ақырғы өлшемді кеңістікте екі өлшемді жиын болсын. R(
t, s, u
) функциясы
t
 G
,
s
G
,
s
 F
, -∞<u<+∞ анықталған болсын. Сызықтық емес интегралдық операторын
F
, -∞<u<+∞ анықталған болсын. Сызықтық емес интегралдық операторын
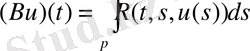 (1)
(1)
Урысон операторы дейді.
1-теорема. R(t, s, u) және R 1 (t, s, u) функциясы Каратеодори шарттын қанағаттандырады, және
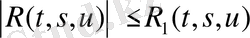 (
t
(
t
 G
, s
G
, s
 F
, -∞<u<+∞)
F
, -∞<u<+∞)
болсын. В
1
операторы мен R
1
(t, s, u) ядросы L
p
(F) (0≤p<∞)
 L
q
(G) (0≤q<∞) және үзіліссіз. Онда интегралдық оператор В L
p
(F) кеңістігінен L
q
(G) кеңістігіне үзіліссіз.
L
q
(G) (0≤q<∞) және үзіліссіз. Онда интегралдық оператор В L
p
(F) кеңістігінен L
q
(G) кеңістігіне үзіліссіз.
Қарапайым түрде В 1 операторы алынып, қасиеті белгілі болған. Осы байланыста Урысон оператор класын ажырату мағынасы болады, оның негізгі қасиеті толық сырттай сызылған. Қазіргі жұмыста Урысон операторының бір класы қарастырылады.
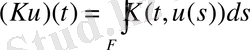 , (2)
, (2)
мұндағы K(t, s) - нақты өлшенетін функция (
t
 G
, -∞<u<+∞) . 1-теоремада берілген
L
p
(F) (1≤p<∞) - дан L
q
(G) (1≤q<∞)
K
операторға үзіліссіз критерий. Салдар сияқты [2] жұмыстың қорытындысынан шығады. K(t, u) ≥0 және q - бүтін сан. Барлық
L
p
=
L
p
(F) (1≤p<∞) - дан ұйғарайық,
L
q
=
L
q
(G) (1≤q<∞), ал
mesF
< ∞ (
mesF -
Лебег өлшемінің F жиыны) жағдайда жалпы шенелмеген
mesF=
1 қоямыз.
G
, -∞<u<+∞) . 1-теоремада берілген
L
p
(F) (1≤p<∞) - дан L
q
(G) (1≤q<∞)
K
операторға үзіліссіз критерий. Салдар сияқты [2] жұмыстың қорытындысынан шығады. K(t, u) ≥0 және q - бүтін сан. Барлық
L
p
=
L
p
(F) (1≤p<∞) - дан ұйғарайық,
L
q
=
L
q
(G) (1≤q<∞), ал
mesF
< ∞ (
mesF -
Лебег өлшемінің F жиыны) жағдайда жалпы шенелмеген
mesF=
1 қоямыз.
1-теорема.
К
операторы
L
p
 L
q
, үзіліссіз болуы үшін келесі шартардың орындалуы қажетті және жеткілікті .
L
q
, үзіліссіз болуы үшін келесі шартардың орындалуы қажетті және жеткілікті .
а)
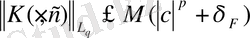
мұндағы
 =I, егер
mesF=
I және
=I, егер
mesF=
I және
 =0, егер
mesF=
∞ ал М- оң тұрақты, с
=0, егер
mesF=
∞ ал М- оң тұрақты, с
 (-∞, +∞) жатпайды.
(-∞, +∞) жатпайды.
б)
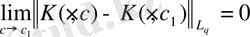
Кез келген с
1
 (-∞, +∞) үшін
(-∞, +∞) үшін
Дәлелдеуі. Қажеттілігі. L p - дан L q - ға К үзіліссіз болсын. Онда «жартылай аддитивтік» қасиетінен Урысон операторы шығады, К шенелген. Сондықтан [3] теореманың негізінен а) шарты орындалады. Функция
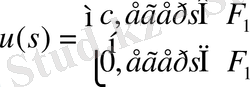
мұндағы
 және
mesF=I
L
p
- ға бағынады, (
Ku
) (
t
) =
K
(
t, c
), осыдан және
К
үзіліссізден б) шарты шығады.
және
mesF=I
L
p
- ға бағынады, (
Ku
) (
t
) =
K
(
t, c
), осыдан және
К
үзіліссізден б) шарты шығады.
Жеткіліктілігі.
а) және б) шарты орындалсын. а) - дан шығады
K
операторы
L
p
⭢
L
q
. Үзіліссіздігін дәлелдейік. Теореманың тұжырымы дұрыс емес дейік. Онда кез келген
ε
0
>0, сондықтан u
n
(s)
 L
p
фукнциясы табылады. Мынадай
L
p
фукнциясы табылады. Мынадай
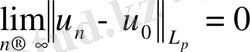 (3)
(3)
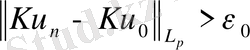 (n=1, 2, …) (4)
(n=1, 2, …) (4)
(3) - тің күшімен {
u
k
}
k
≥0
 L
p
үйір функциясы біршенді абсолют үзіліссіз норма болады. Онда кез келген
ε
>0 [3] леммаға келісіп және а) δ>0 әсер етеді, мынадай
mesD<δ
(
D
L
p
үйір функциясы біршенді абсолют үзіліссіз норма болады. Онда кез келген
ε
>0 [3] леммаға келісіп және а) δ>0 әсер етеді, мынадай
mesD<δ
(
D
 F
) шартынан теңсіздік шығады:
F
) шартынан теңсіздік шығады:
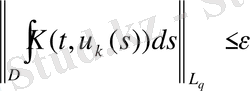 (
k
=0, 1, 2, …) (5)
(
k
=0, 1, 2, …) (5)
ξ саны үшін F ξ жиынын көрсетіп, егер mesF< ∞ F бірқалыпты аламыз, ал егер mesF= ∞ болса (6) шартын аламыз.
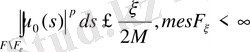 . (6)
. (6)
мұндағы М - а) шартының саны. Жиын барысында Лебег интегралының анықтамасынан ақырсыз өлшем жиыны шығады.
(3) - тің күшімен n 1 =n 1 (ξ) табылады. Мынадай
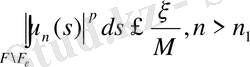 . (7)
. (7)
(6), (7) қатынасы а) шартын береді. n=0 және n>n 1 болғанда.
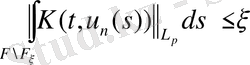 (8)
(8)
Белгілеуі
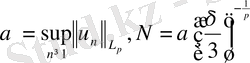 ,
,
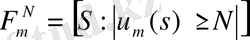 (m=0, 1, 2, …) .
(m=0, 1, 2, …) .
Мұндағы δ - (5) - тің саны
mesF
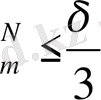 ,
m=0, 1, 2, … (9)
,
m=0, 1, 2, … (9)
аламыз.
Сондықтан u n (s) функциясынан u 0 (s) - тан L p шығады, онда {u n (s) } F ξ өлшемінен u 0 (s) шығады және {u n (s) } - ті тізбекке бөлуге болады. Белгілеуі {u n } n ≥1 арқылы және u 0 (s) - тің F ξ - ға жинақты.
Онда
Егоров
теоремасынан шығады,
F
δ
 F
ξ
өлшем жиыны қатысады, мынадай
F
ξ
өлшем жиыны қатысады, мынадай
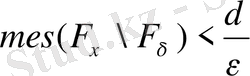
(10) және
F
δ
жиынынан u
n
(s) тізбегінен u
0
(s) бірқалыпты
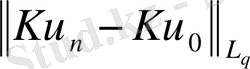 ұйғарайық.
ұйғарайық.
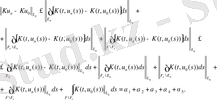 (11)
(11)
Mұндағы
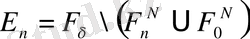
(9) және (10) - нан шығады,
mes
(
F
ξ
\
L
n
) <δ (n=1, 2, …) . Сондықтан (5) және (8) - дің негізін аламыз.
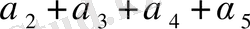 қосындысы n>n
1
- ден кіші 4
ξ
қарағанда. Бірінші қосылғыш (11) - ден кіші екенін көрсетейік.
ε
-ге қарағанда б) шартынан шығады, мынадай δ
1
=δ
1
(
ξ
) >0, c-c
1
< δ
1
теңсіздігінен шығады.
қосындысы n>n
1
- ден кіші 4
ξ
қарағанда. Бірінші қосылғыш (11) - ден кіші екенін көрсетейік.
ε
-ге қарағанда б) шартынан шығады, мынадай δ
1
=δ
1
(
ξ
) >0, c-c
1
< δ
1
теңсіздігінен шығады.
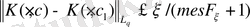 . (12)
. (12)
Өйткені {u n (s) } жинақтылық тізбегінен u 0 (s) F δ -ға бірқалыпты, n 0 =n 0 (δ 1 ) табылады. Мынадай
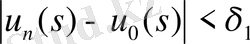 s
s
 F
δ
, n>n
0
. (13)
F
δ
, n>n
0
. (13)
(12) және (13) - тен n>n 0 -де α 1 ≤ ξ аламыз. Сондықтан
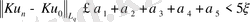 , n>max(n
0
, n
1
) .
, n>max(n
0
, n
1
) .
ξ<0, 1∙ξ теңсіздік болсын, онда (4) қайшылық аламыз. Теорема дәлелденді.
2-теорема. mesF< ∞ және K : L ∞ →Lp, Lp, ⭢L q, p =∞ болсын
1)
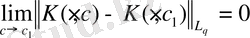 , с
1
, с
1
 (-∞, +∞) үшін,
(-∞, +∞) үшін,
2) K үзіліссіз,
3) K толық үзіліссіз.
Дәлелдеуі: Жеткілікті келесі имплекацияны дәлелдеу 1) =>2) =>3) өйткені 2) -ден 1) шығады.
1) шарт орындалсын. Онда кез келген ξ>0 δ= δ(ξ) >0 мынадай c-c 1 < δ теңсіздігінен шығады:
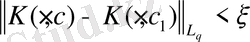 . (14)
. (14)
{u
n
(s) }
n≥0
 L
∞
болсын және
L
∞
болсын және
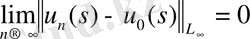 (15)
(15)
(15) үшін ε>0 n 0 =n 0 (ε) . Мынадай
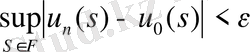 (16)
(16)
барлық n>n 0 -де.
Келесі
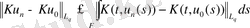 .
.
(14) және (16) теңсіздігінен шығады
 , n>n
0
, n>n
0
1) =>2) орынды екендігін көрсетеді.
K үзіліссіз болсын, K операторы компакт екенін дәлелдейік.
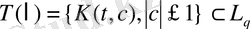
үйір функциясын қарастырайық. Т(
 ) тізбегі {
K
(t, c
n
) } болсын. c
n
<
) тізбегі {
K
(t, c
n
) } болсын. c
n
<
 күшпен
күшпен
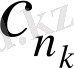 тізбек астына әсер етеді. c
0
жинақты, c
0
≤
тізбек астына әсер етеді. c
0
жинақты, c
0
≤
 . Онда
K
үзіліссіздігінен шығады:
. Онда
K
үзіліссіздігінен шығады:
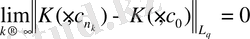 .
.
Сонымен, Т(
 ) үйір функциясы L
q
-де компакт. Сондықтан Т(
) үйір функциясы L
q
-де компакт. Сондықтан Т(
 ) үшін Рисса теоремасының шарты орынды.
) үшін Рисса теоремасының шарты орынды.
1)
М=M
(
 ) саны және
) саны және
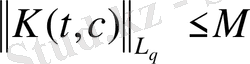 . (17)
. (17)
2) Кез келген ε>0 әсері δ=δ(ℓ, ε) >0 мынадай
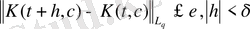 . (18)
. (18)
3) Кез келген ε>0 әсері N = N (ℓ, ε) >0 мынадай
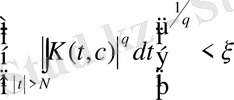 (19)
(19)
барлық c<ℓ үшін. Мұндағы
K
(
t, c
) =0, егер t
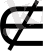 G.
G.
L
∞
-да
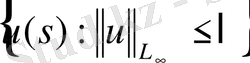 шар болсын. Онда (17) - (19) дан шығады:
шар болсын. Онда (17) - (19) дан шығады:
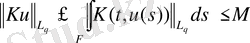 ,
,
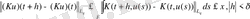 ,
,
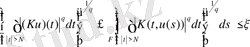
барлық u(s) үшін,
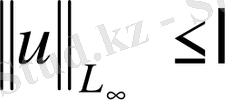 . Сондықтан Рисса теоремасының жиыны
. Сондықтан Рисса теоремасының жиыны
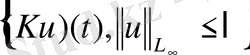 туралы
L
q - де компакт. Теорема дәлелденді.
туралы
L
q - де компакт. Теорема дәлелденді.
Ескерту: Егер mesF =∞, онда K операторы L ∞ - ден L q-ға әсер етеді, және K ( t, u ) ≡0.
Урысон операторының бір классының
үзіліссіздік критерийлері
G және F - ақырғы өлшемді кеңістікте екі өлшемді жиын болсын. Функция
K
(t, s, u) t
 G,
G,
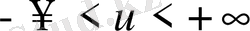 - те анықталған болсын. Сызықтық емес интегралдық операторды
- те анықталған болсын. Сызықтық емес интегралдық операторды
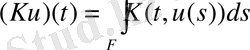 (1)
(1)
Урысон операторы деп атайды, оның өзінің қосымшасы маңызды. (1) операторға жорамал жасап, бірнеше интегралдық Урысон оператор класын құрайды. Шенелгендікті анықтағанда үзіліссіз және толық үзіліссіз Урысон операторы көбінесе қолданылады.
«Мажоранты» операторы [1, 2] танымал қасиет. Осы байланыста зерттеу операторы (1) түрде керекті мән алады.
L
p
(F) және L
q
(G) операторларын
K
- да шенелген және компакт болатын сұрақты қарастырайық. (1) - түрдегі оператор [3] жұмыста қарастырылған, мұндағы
K
(t, u)
 0.
0.
q - бүтін, K операторы L p (0, 1) - ден L q (0, 1) - ге шенелген және үзіліссіздігі қажетті және жеткілікті шартта берілген.
Оператордың шенелген шартты, осы жұмыста көрсетілген, біздің бірінші теоремадан шығады, K (t, u) ядросында және q санында шенелгендігі алынады.
Барлық жерде L
p
=L
p
(A) (1
 p
p
 ∞) L
p
= L
q
(G) (1
∞) L
p
= L
q
(G) (1
 q
q
 ∞) деп ұйғарайық,
mes
F<∞ жағдайын жалпы шенелмеген
mes
F=1 қойсақ
mes
F бар жерде F-жиын
Лебег өлшемі.
∞) деп ұйғарайық,
mes
F<∞ жағдайын жалпы шенелмеген
mes
F=1 қойсақ
mes
F бар жерде F-жиын
Лебег өлшемі.
1-теорема.
К
операторы L
p
 L
q
бейнелесін., онда К операторы шенелген болуы үшін келесі шарттардың орындалуы қажетті және жеткілікті. a)
L
q
бейнелесін., онда К операторы шенелген болуы үшін келесі шарттардың орындалуы қажетті және жеткілікті. a)
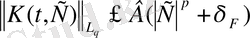 ,
,
мұндағы
 =1, егер
mes
F=1 және
=1, егер
mes
F=1 және
 =0, егер
mes
F=∞, ал В - оң тұрақты. С
=0, егер
mes
F=∞, ал В - оң тұрақты. С
 (-∞, +∞) - ған байланысты емес.
(-∞, +∞) - ған байланысты емес.
Дәлелдуі: Қажеттілігі.
L
p
 L
q
және шенелген болсын, онда b - оң саны табылады.
L
q
және шенелген болсын, онда b - оң саны табылады.
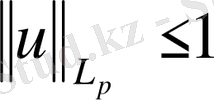 теңсіздігінен шығады.
теңсіздігінен шығады.
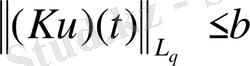 (2)
(2)
mes
F=1 болсын. Онда (2)
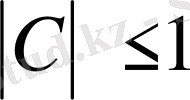 -ге болғанда
-ге болғанда
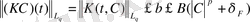 ,
,
мұндағы B=2b.
Жеткілікті шарт.
а) [4] Минковский теңсіздігінен және шарттынан жинақтылығы шығады. а) :
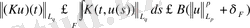
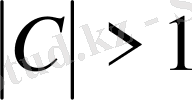 болсын.
болсын.
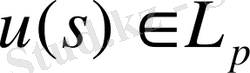 функциясын анықтаймыз.
функциясын анықтаймыз.
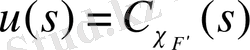 , (3)
, (3)
мұндағы
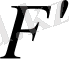 - жиынның ішігдегі F жиын, мынандай
- жиынның ішігдегі F жиын, мынандай
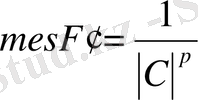
ал
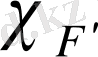 - оның характеристикалық функциясы. Осы сияқты
- оның характеристикалық функциясы. Осы сияқты
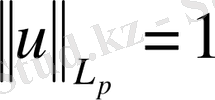 , онда (1), (2) аламыз.
, онда (1), (2) аламыз.
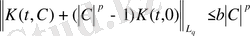 (4)
(4)
онда
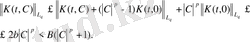
Енді
mes
F=∞ болсын. Онда 0
 L
p
- дан шығады.
K
(t, 0) =0. Сондықтан С=0 теңсіздігінен
L
p
- дан шығады.
K
(t, 0) =0. Сондықтан С=0 теңсіздігінен
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz