Жылулық сәуле шығаруды зерттеу әдістері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Кіріспе

Жылулық сәуле шығару теориясы Кирхгофтың 1859ж. жылулық сәуле шығарудың негізгі заңын ашқан кезден басталады. Ол қара дене концепциясын және оның моделін ұсынды. Осы уақыттан бастап 20ғ. басына дейін қара дененің сәуле шығару проблемасы физикада ең бір өзекті проблема ретінде қарастырылды. Бірақта сәуле шығарудың классикалық теориясы жылулық сәуле шығару заңдарын, атомдар мен молекулалардың спектрлерін қанағаттанарлық дәрежеде түсіндіре алмады. Осы проблемаларды сәуле шығарудың кванттық теориясы аясында шешу мүмкін болды. Сәуле шығарудың кванттық теориясының басталуына жол ашқан бірінші жұмысты Планк жариялады (1900) . Ол ең алғаш атомдық жүйелер электромагниттік толқындарды үздіксіз емес, үлестермен, кванттармен шығарады деп ұйғарып тепе-теңдіктегі жылулық шығарылған сәуле спектріндегі энергияның үлестірілуі үшін формуланы қорытып шығарды.

Жылулық сәуле шығару - бұл қыздырылған дененің шығарған жарығы. Күннің жарығы, май шамның жалыны, қыздыру лампасының жарығы, электр доғасы, адам денесінің инфрақызыл сәулесі - мұның бәрі жылулық сәуле шығару мысалдары. Жылулық сәуле шығару әртүрлі жарық көздерінде пайдаланылады. Ол көптеген физикалық жүйелердегі жылулық балансқа едәуір ықпалын тигізеді, мәселен, Жер бетінің орташа температурасын анықтайды. Сәуле шығарудың осы түрінің теориясы физнка үшін маңызды, өйткені, бір жағынан жылулық сәуле шығару әмбебап, оның табиғаты нақты материалмен де, тіпті атомның кұрылысымен де байланысты емес, ал екінші жағынан, жылулық сәуленің пайда болуына жарық пен заттың іргелі термодинамикасы себепші болады да, осы сәуленің қасиеттері атомдардың жарықты кезкелген мөлшерде емес, тек қатаң белгілі дискреттік үлестермен (кванттармен) шығаруға немесе жұтуға қабілетті екендігіне тікелей нұсқайды.

Жылулық сәуле шығару және оның негізгі заңдары

Негізгі тәжірибелік деректер. Жылулық сәуле шығаруды зерттеу әдістері. Қатты қыздырылған денелердің жарық шығара бастайтындығы белгілі. Дене температурасын өсіргенде жарқыраудың жарықтылығы артады, ал оның түсі қызылдан аққа дейін өзгереді. Осындай заңдылықтарды, мысалы, электр плитасы спиралының немесе қыздыру лампасы қылсымының қыздырылуын бақылап көруге болады.

Жылулық шығарылған сәулеге тән белгі оның кең тұгас спектрі болады.

1. 1-суретте қыздырылған денелердің шығарған сәулесінің спектрлері көрсетілген (Люммер және Прингсгейм 1899ж. өлшеген) . Графиктерден сәуле шығаратын дененің температурасын өсіргенде жылулық шығарылған сәуленің толық қуатының өсетіндігі және спектрлік тығыздық максимумының спектрдің қысқа толкынды аймағына ығысатындығы

айкын көрінеді. 19-20 ғасырлар аралығында физика алдына жылулық

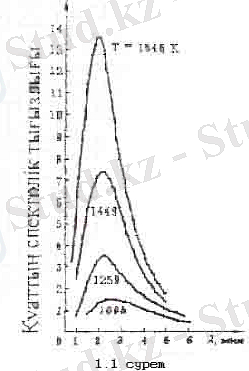
сәуле шығару спектрін қалай түсіндіруге болады деген мәселе койылды. Осы проблеманы зертгеу кванттык көрністердің пайда болуына алып келгендігі белгілі.

Жылулық сәуле шығару және оның сипаттамалары. Электромагниттік сәуле шығарудың табиғатта ең көп тараған түрі жылулық сәуле шығару болып табылады. Жылулық сәуле заттың ішкі энергиясы есебінен шығарылады, сондықтан да ол температурасы 0 К-нен өзгеше кезкелген температурадағы барлык денелерге тән.

Жылулық сәуле шығару дененің ішкі энергиясының кемуіне, демек, дене температурасының төмендеуін, сууын туғызады. Энергияның ұзақ уақыт бойы шығарылу мүмкіндігін қамтамасыз ету үшін, оның шығынының орнын толтырып отыру кажет. Бірақ сәуле шығарумен катар дененің өзі баска денелер шығарған энергияның бір бөлігін жұтады. Энергияның жұтылуы дененің ішкі энергиясының өсуін, демек, температураның жоғарылуын туғызады. Денелердің энергияны тұрақты түрде шығаруы және жұтуы оңашаланған термодинамикалық жүйеде ақыр аяғында белгілі бір температураның орнығуына алып келеді; осы температура жағдайында дене шығарғанда энергияның кемуі, жұтқанда оның өсуімен теңгеріледі, шығарылатын және жұтылатын энергия спектрі уақытқа байланысты өзгеріссіз қалады. Сәуле шығарудың осы түрі тепе-теңдік сәуле шығару деп аталады.

Термодинамикалық жүйенің уақыт өткенде параметрлері өзгермейтін күйі термодинамикалық тепе-тендік күй деп аталады. Термодинамикалық тепе-теңдікте тұрған жүйе үшін мына қасиеттер тән: жылулық сәуле шығару үшін оңашаланған жүйенің термодинамикалық тепе-тендік күйі белгілі уақыт өтісімен орнығады; егер жүйе термодинамикалық тепе-теңдікке жетсе және сырткы жағдайлар өзгермейтін болса, онда жүйе өзі өз бетінше осы күйден шыға алмайды.

Сәуле шығарудың барлық басқа түрлері (бұларды люминесценция деп жалпы ортақ атпен біріктіреді) мұндай касиетке ие емес. Мысалы, хемилюминесцияда сәуле шығару химиялык түрленулерде бөлінетін энергия есебінен пайда болады. Хемилюминесценция жағдайында сәуле шығару процесі химиялық реакция жүріп біткен уақытка дейін ғана созылады. Жылулық тепе-теңдік химиялық процесс онымен бірге хемилюминсценция біткеннен кейін ғана орнайды. Дәл осы жағдай электро-, фото- және катодлюминесценция жағдайларында да орын алады. Сонымен, сәуле шығарудың барлық түрлері ішінен тек жылулық сәуле шығару ғана тепе-тендікте бола алады.

Жылулық сәуле шығару дененің температурасына тәуелді, өйткені ол атомдар мен молекулалардың бейберекет жылулық қозғалысының салдары болып табылады.

Денелердің сәуле шығарғыштық және сәуле жұтқыштық кабілеті. Әртүрлі денелер жарықты әртүрлі жұтады. Қара денелер жарыкты күшті жұтады, ақ денелер нашар жұтады. Бұған дәлел ретінде көптеген мысал келтіруге болады. Мысалы, күн сәулесіне қойылған бөшкедегі су егер бөшке қара түске боялған болса, онда тезірек жылиды.

Дененің сәуле жұтқыштық қабілетін сандық сипаттау үшін мына шаманы енгіземіз:

\[a={\frac{W_{\omega\phi}}{W_{\partial{\bar{m}}}}}\]

(1. 1)

Мұндағы W _түс - денеге түсетін жарық энергиясы, W _жұт - денеде жұтылған жарық энергиясы. а шамасын дененің жұту қабілеттігі деп атаймыз. Жұту қабілеттілігін тәжірибе жүзінде дененің кыздырылуы бойынша өлшеуге болады.

Мөлдір емес денелер үшін жұтылған және шағылған жарық энергияларының қосындысы түскен жарық ағыны энергиясына тең:

W _түс =W _шағ +W _жұт ,

сондыктан өлшемділіксіз а шамасы мына аралыкта жатады: 0 ≤ а ≤ 1. Шектік жағдайларды былай атауға болады: а = 0 - «ақ дене», а = 1 - «қара дене».

Тәжірибеден бір дененің жұту қабілеттілігі дене температурасы өзгергенде және оған түсетін υ = ω /2 π жарық жиілігі өзгергенде өзгеретіндігі көрінеді. Демек, әрбір денені α = α ( ω , Τ ) қайсыбір функциямен сипаттауға болады. Әрине, әртүрлі денелерде осы функциялар тіптен әртүрлі болады.

Жарықтың шығарылуы. Қандайда бір кыздырылған денені, мысалы, қыздыру лампасының қатты қыздырылған қылсымын карастырайык. Дене бетінің ауданы ds элементін бөліп алып беттің осы бөлігінің жиіліктердің ω - ден ω+d ω -ге дейінгі аралығында шығаратын сәуле қуатын dP _шығ арқылы белгілейік.

dP _шығ шамасы ds және dω шамаларына пропорционал болатындығы түсінікті. Сондыктан мына өрнекті жазуға болады:

dP _шығ = rdωds (1. 2)

Осы формуладағы пропорционалдық r коэффициентті дененің сәуле шығарғыштык қабілеттілігі деп атаймыз. Сәуле шығарғыштық қабілеттілікте сәуле жұтқыштық қабілеттілік сияқты дененің Т температурасынан және ω жарықтың жиілігінен тәуелді, яғни r = r ( ωT ) .

Кирхгоф заңы

Тепе-теңдік жылулық сәуле шығару. Т температураға дейін қыздырылған ішіне қуыс істелген дене бар болсын (1. 2-сурет) . Қуыстың қабырғалары жылулық сәуле шығаратындықтан, қуыс осы сәулемен толтырылған болады. Дене температурасы тұракты етіп ұсталатын стационарлық жағдайларда қуыстағы жылулык сәуленің сипаттамаларының тұрақты және белгілі мәндері болады, дәлірек айтқанда, қуыс қабырғаларының жарық шығару және жұту процестері өзара бірін-бірі теңестіретіндей мәндері болады. Басқаша айтканда, стационарлық жағдайларда қуыс қабырғалары мен оның ішіндегі сәуле арасында жылулық тепе-теңдік орнайды. Осы жағдайда қуыстағы жылулық сәуле тепе-теңдік сәуле деп аталады.

Қуысты сырткы кеңістікпен қосатын кішкене тесік істеп тепе-теңдік жылулық сәулені зерттеуге болады. Осы тесік арқылы тепе-теңдік жылулық сәуле қуыстан сыртқа шығатын болады және оның сипаттамаларын өлшеуге болады.

Кирхгоф заңы. 1859ж. неміс физигі Г. Кирхгофтың ашқан заңына сәйкес тепе-тендік күйде сәуле шығарғыштық қабілеттіліктің сәуле жұтқыштық қабілеттілікке қатынасы дене табиғатына тәуелді емес:

\[\frac{r(w,T)}{a(w,T)}=f(\omega,T)\]

Equation. 3 (1. 3)

Мұнда f ( ω, T ) - барлық денелер үшін бірдей жарық жиілігі мен дене температурасының әмбебап функциясы, қара дененің сәуле шығарғыштық қабілеттілігі деп аталады. Осы атаудың мағынасы қара дене аныктамасынан түсінікті, осы анықтамаға сәйкес осындай дене үшін α ( ω, T ) = 1, демек, r ( ω, T ) = f ( ω, T ) . Алғашында Кирхгоф осы заңды термодинамика түсініктерін пайдаланып теориялық қорытып шығарды. Кейіннен осы заң тәжірибеде расталды.

Кирхгоф заңын растайтын теориялық ой-пікірлерді қарастырайық. Тепе-теңдік жылулық сәулемен толтырылған қуыс ішінде қандай да бір дене бар деп ұйғарайық. Сірә, жылулық тепе-теңдік күйдегі дененің жұтатын сәуле қуаты оның шығаратын қуатына тең:

dP _жұт = dP _шығ , (1. 4)

өйткені бұлай болмаған жағдайда дене қыздырыла немесе салкындай басталар еді, ал бұл тепе-тендіктің бұзылуына әкелер еді. Дененің сәуле шығарғыштық және жұтқыштық кабілеттіліктерінің анықтамаларын пайдаланып, мынаны жазамыз:

dP _жұт = αdP _шығ , (1. 5)

dP _шығ =rdvds = rdwds (1. 6)

мұндағы r - сәуле шығарғыштык қабілеттілік, α - сәуле жұткыштық қабілеттілік, dP _түс - дене бетінің ds элементіне түсетін ω -ден ω=dω -ге дейінгі спектрлік аралығындағы жиілігі бар сәуле қуаты. (1. 4) -(1. 6) өрнектерінен мына өрнек шығады.

αdP _түс = rdωds (1. 7)

Енді біздің сыншы денені мөлшері мен пішіні дәл осындай баска денемен алмастырайық. Жылулық сәуле шығару сипаттамалары өзгеріссіз қалатындыктан (1. 4) - (1. 7) формулалары, α және r коэффициенттерінің енді басқа мәндері болғандығына қарамастан, күшінде қалады. Сонымен (1. 7) формуладағы r және а -дан баска барлық шамалар инвариант. Бірақ сонда r/α қатысы да инвариант болуы тиіс, бұл Кирхгоф заңының мазмұнын аныктайды.

Тепе-тендік жылулық сәуле шығарудың спектрлік тығыздығы. Тепе-тендік жылулық сәуле ρ ( ω, Т ) спектрлік тығыздықпен сипатталады; ол кеңістіктің бірлік көлеміне және ω жиілік маңындағы ені dω жиіліктердің шексіз кіші аралығына келетін Т температурада шығарылатын теп-тендік сәуле энергиясы ретінде карастырылады. V көлемдегі және жиіліктердің ω -ден ω + dω - ге дейінгі жиіліктер аралыгындағы жылулық сәуле шығару энергиясы мынаған тең

dw = Vρ ( ω, T ) dω. (1. 8)

dw шамасы Дж-мен өлшенеді. (1. 8) формуланы ρ ( ω, T ) функцияның анықтамасы ретінде карастыруға 6олады.

ρ ( ω, T ) функция қара дене шығаратын сәуленің спектрлік тығыздығы деп атайды, өйткені осы функция қара дененің сәуле шығарғыштық қабілеттілігі мағынасына ие Кирхгофтың әмбебап f ( ω, T ) функциямен бірмәнді байланысқан.

Люммер мен Прингсгейм тепе-тендік жылулық сәуле шығарудың спектрлік тығыздығын экспериментгік зерттеді. Осы зертгеулердің нәтижелері 1. 1-суретте көрсетілген.

Тепе-теңдік жылулық сәуле шығарудың ρ ( ω, T ) спектрлік тығыздығын теориялық есептеуге көшейік.

Рэлей-Джинс формуласы

Тепе-теңдік жылулық сәуле шығарудың термодинамикасы. ρ ( ω, T ) функциясын теориялық есептеуді өрістің еркіндік дәрежелері бойынша энергияның теңдей үлестірілуі жайында термодинамикадан белгілі заң негізінде орындауға болады. Осы заңға сәйкес жылулық тепе-тендік күйде жүйенің әрбір еркіндік дәрежесіне орташа алғанда kТ/ 2-ге тең бірдей энергия келеді. Мұндағы Т - жүйенің термодинамикалық температурасы, k - Больцман тұрақтысы. Осы заңды жылулык сәуле шығаруға қолдану үшін тұйық қуыстағы электромагниттік өрістің еркіндік дәрежесін есептеу қажет.

Есептеудің негізгі идеясы бойынша қуыстағы тепе-теңдік жылулык сәуле шығаруды тұрғын толқындардың жиынтығы түрінде келтіріледі. Шын мәнінде мәселе тепе-теңдік сәуленің стационарлык кеңістіктің құрылымын элементар қарапайым құрылымдарға - синусоидалық тұрғын толқындарға спектрлік жіктеу жайында болып отыр.

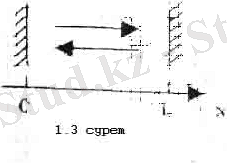Мына екі жағдай маңызды. Бірінші-тепе-теңдік жылулық сәуленің кеңістіктік құрылымы стационар, екінші - қуыс қабырғаларына түсетін сәуле энергиясы қабырғаның шығаратын энергиясына тең. Осы екі шарт орындалатын қарапайым жүйеге қос параллель айна - оптикалық резонатор жатады ( 1. 3-сурет) . Осындай резонатордағы жарық өрісін тұрғын толқындардың дискреттік санамалы жиыны түрінде өрнектеуге болады. Әртүрлі тұргын толқындардың саны өрістің еркіндік дәрежесінің ізделіп отырған санын анықтайды.

Сонымен екі жазық айнаның ортасындағы жарық өрісін карастырайық. Айналардың ара қашықгығын L арқылы белгілейміз. x осін айналардың бетіне нормаль бойынша бағыттаймыз. Жазык резонатордағы жарық өрісі бірөлшемді толкындық тендеуді қанағаттандырады:

\[\frac{\P^{2}E}{\P\!\Vert x}-\,\frac{1}{c^{2}}\frac{\P^{2}E}{\P\!\Vert t^{2}}=0\]

(1. 9)

Айналарды идеал өткізгіштер деп есептеп, шекаралық шарттарды мына түрде жазамыз:

E (0, t ) = E ( L, t ) = 0 (1. 10)

Осы шекаралық шарттармен (1. 9) теңдеуінің шешімі мынадай болады:

E ( x, t ) = A ( t ) sin k _x x . (1. 11)

(1. 10) -ды (1. 1) -ға қойып A ( t ) амплитуда үшін теңдеуді аламыз

\[{\frac{\parallel^{2}A}{\parallel t^{2}}}+c^{2}k_{x}^{2}A=0\]

(1. 12)

Сонымен, амплитуда гармоникалық осцилятордың теңдеуіне бағынады. Осы тендеудің шешімі:

A ( t ) = A ₀ cos( ωt+φ ), ω = ck _x (1. 13)

Екінші жағынан, (1. 11) -ді (1. 10) -ға қойып, мына тендеуді аламыз:

sin k _x L = 0,

Осыдан k _x L = m _x π , m _x = 1, 2, 3, . . . (1. 14)

Демек

\[w=c k_{x}=m_{x}{\frac{\pi c}{L}}\]

, m _x = 1, 2, 3, . . . (1. 15)

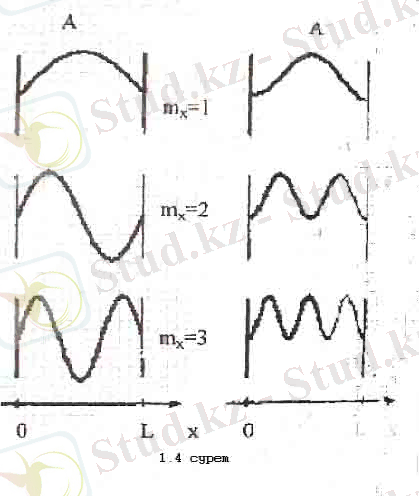Сонымен, резонатордағы жарық өрісінің құрылымы толқындардың дискреттік жиыны түрінде болады. Жарык нтенсивтігінің белгілі кеңістіктік үлестірілуімен сипатталатын әрбір тұрғын толқынды «өріс осцилляторы» деп атауға болады. Жарық өрісінің бірнеше қарапайым кұрылымы 1. 4-суретте көрсетілген. Мұндағы маңызды нәрсе, ол өріс, осцилляторлары резонаторда санамалы жиын құрап тұрады, демек оларды нөмірлеуге болады. Әр түрлі осцилляторлар бір-бірінен тәуелсіз болатындықтан (бұлардың амплитудалары кез-келген мәнге ие) бұлардың толық саны өрістің еркіндік дәрежесінің санын анықтайды.

(1. 14) формулаға сәйкес, k _х толқындық сандар кеңістігінде әрбір өріс осциллятордың үлесіне мөлшері ∆ k = π/L болатын ұяшық (1. 5-сурет), тиеді мұндағы L - резонатордың ұзындығы.

Енді қарастыруды үш кеңістіктік координаттар жағдайына таратып, айнадан істелген кабырғалары бар куб пішінді куыс ішіндегі жарык өрісін қарастырамыз (1. 6-сурет) . Куб кырының ұзындығы L , көлемі V = L ³ , координат остері кубтың қырлары бойымен бағытталған болсын.

Өрістің әрбір декарттық Е _х , Е _у , Е _z құраушылары үшін мына толқындық теңдеу орындалады:

\[\mathrm{D}E-{\frac{1}{c^{2}}}{\frac{\P^{2}E}{\P t^{2}}}=0\]

(1. 16)

мұндағы

\[\mathbf{D}={\frac{\mathbf{q}[^{2}}{\|x^{2}}}+{\frac{\mathbf{q}^{2}}{\|y^{2}}}+{\frac{\mathbf{q}\|^{2}}{\partial z^{2}}}\]

- Лаплас операторы. (1. 16)

теңдеудің шешімін мына түрде іздестіреміз:

E ( x, y, z, t ) = A ₀ sin( k _x x ) sin( k _y y ) sin( k _z z ) cos( ωt=φ ) (1. 17)

(1. 17) - ні (1. 16) - ға қойғанда мына тендеу алынады:

\[k_{x}^{2}+k_{y}^{2}+k_{z}^{2}\circ\;k^{2}=\omega^{2}\;/\;c^{2}\]

(1. 18)

Бұл толқындық санның k модулін және жарық толқыны ω жиілігін өзара байланыстыратын дисперсиялық теңдеу деп аталатын теңдеу.

(1. 14) - ке ұқсас, шекаралық шарттардан мына қатыстар алынады:

k _x L = m _x π , k _y L = m _y π , k _z L = m _z π , (1. 19)

мұндағы m _x , m _y , m _z , - кез - келген жай сандар, яғни

m _x , m _y , m _z = 1, 2, 3, …. (1. 20)

k _x , k _y , k _z шамаларын жарық толқынының

\[\begin{array}{l}{\hookrightarrow}\\ {\bigcup_{K}}\end{array}\]

толқындық векторының декарттық құраушылары ретінде қарастыруға болады.

Сонымен, үшөлшемді жағдайда өріс осцилляторы жай сандардың m _x , m _y , m _z

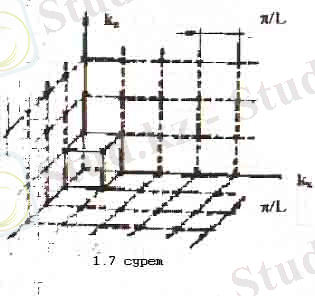
үштігімен сипатталады. Толқындық сандар кеңістігінде (« k -кеңістік») өріс осциллято-рын бейнелейтін сурет 1. 7-суретте көрсетілген. Осы суреттен k - кеңістік түгелдей әрқайсысының көлемі

v _k = ( π/L ) ³ (1. 21)

болатын кубиктерге бөлінгендігі көрінеді, сонда әрбір жеке кубике өзінің осцилляторы сәйкес келеді.

Енді өрістің еркіндік дәрежесінің толық санын есептеп шығару қиын емес. 0 - ден ω - ге дейінгі жиіліктер ауқымын алып жататын жарық өрісін қарастырайық. (1. 18) дисперсиялық теңдеуге сәйкес өрістің толқындық сандары 0 - ден k = ω / с - га дейінгі ауқымды алып тұрады. Толқындық сандар кеңістігіндегі осы аймақ радиусы k шар түрінде болады, ал оның көлемі 4 πk ³ /3 болады. (1. 17) формулаға сәйкес k _x , k _y , k _z сандар, мысалы

k _x , k _y , k _z > 0 (1. 22)

сай келеді. Берілген аймаққа (толқындық сандар кеңістігінің оң октанты) радиусы k шардың 1/8 бөлігі ғана кіреді, осы бөліктің көлемі

\[V_{k}={\frac{1}{6}}\pi k^{3}\]

(1. 23)

Өрістің ізделіп отырған осцилляторлар саны, сірә, k кеңістіктегі өрістің барлық осцилляторлары алып жататын V _k көлемнің бір осцилляторға сәйкес келетін ұяшықтың v _k көлеміне қатынасына тең.

Осы санды N' арқылы белгілеп, былай жазуға болады.

\[N^{!}=V_{k}~/v_{\ k}\]

Equation. 3 (1. 24)

(1. 21), (1. 23), (1. 18) - ді пайдаланып, осы шаманы былайша жазуға болады:

\[N^{!}=\frac{W^{3}L^{3}}{6\pi^{2}c^{3}}\]

(1. 25)

Сонымен, (1. 25) формула көлемі L ³ кеңістік аймағын және 0 - ден ω - ге дейінгі жиіліктер аралығын алып жаткан өрістің осцилляторлары санын анықтайды. Осы формула жарық толқындарының мүмкін болатын таралу бағыттарымен байланыскан өрістің еркіндік дәрежесінің санын береді. Бірақта белгілі бағытта таралатын толқынның екі тәуелсіз поляризация күйі болады (мысалы, х осі бойымен таралатын жазық толқын, жалпы алғанда, Е _z , Н _у және Е _у , Н _z толқындарының суперпозициясы болып табылады) . Сондықтан жарық өрісінің еркіндік дәрежесінің толық саны N' санынан екі есе артық және ол мына шамаға тең болады:

\[N={\frac{w^{3}L^{3}}{3\pi^{2}c^{3}}}\]

(1. 26)

Енді ω -ден ( ω+d ω ) -ге дейінгі аралыққа келетін өрістің еркіндік дәрежесінің санын есептейік. (1. 26) теңдігінің екі бөлігінен дифференциал алып, мынаны табамыз:

\[d N+{\frac{w^{3}L^{3}}{p^{2}c^{3}}}d\omega\]

(1. 27)

Сонымен, тепе-теңдік жылулық шығарылған сәуленің еркіндік дәрежесінің санын есептеуге арналған есеп шешілді. Осы нәтижені пайдаланып. тепе-теңдік жылулық сәуленің спектрлік тығыздығын, яғни кеңістіктің бірлік көлеміне және ω -ден ( ω+dω ) -ге дейінгі спектрлік аралыққа келетін сәуле энергиясын мына түрде өрнектеуге болады:

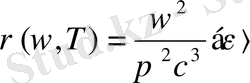(1. 28)

мұндағы ‹ε› - өріс осцилляторына тиісті орташа энергия.

Рэлей-Джинс формуласы. Еркіндік дәрежелер бойынша энергияның теңдей үлестірілуі заңына сәйкес, тепе-теңдік жылулық күйдегі осциллятордың орташа энергиясы

\[\langle s\rangle=k T\]

Equation. 3 (1. 29)

мұндағы k - Больцман тұрақтысы, Т - жүйенің температурасы. Мәселен, механикалық осциллятор үшін орташа кинетикалық энергия орташа потенциалдық энергияға тең және ол kТ /2 -ге тең.

Екі жағдайда да осциллятордың толық орташа энергиясы kТ - ға тең.

(1. 29) -ды (1. 28) -ге қойып мынаны аламыз

\[r\left(w,T\right)={\frac{w^{2}}{\pi^{2}c^{2}}}k T\]

(1. 30)

Тепе-тендік жылулық шығарылған сәуленің спектрлік тығыздығы үшін осы өрнек Рэлей-Джинс формуласы деп аталады.

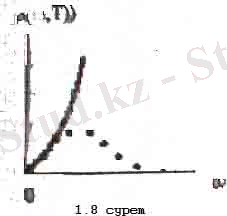1. 8-суретте ρ ( ω, T ) үлестірілуінің тәжірибеде өлшенген түрі және Рэлей-Джинс формуласы бойынша тұрғызылған теориялық қисығы көрсетілген. Эксперименттік және теориялық тәуелділіктердің сапалық айырмашылығы көрініп тұр, демек, Рэлей-Джинс формуласы жиіліктердің барлық аймағында дұрыс деп қабылдауға болмайды. Дегенмен ұзын толқындық аймақта осы формула тәжірибемен жақсы үйлеседі. Осы жағдай және де Рэлей-Джинс формуласының негізіне алынған қағидалардың айқындылығы мен қарапайымдылығы төменгі жиіліктер аймағында осы формула дұрыс және жиіліктердің бүкіл аймағы үшін жарамды болатын толығырақ формула табылғанда ол тиісгі шектік жағдайда Рэлей-Джинс формуласына ауысуы тиіс деп ұйғаруға мүмкіндік береді.