Фурье қатарлары мен стереометрия: ортогоналдық, периодтық жіктеу және көпжақтардың ауданы мен көлемі


Жоспары :
1. Периоды 2п - ге тең болған функцияның Фурье қатарына жіктеу
2. Периоды 2I- гн тең болған функцияны Фурье қатарына жіктеу
- Периодсыз функцияны Фурье қатарына жіктеу
Әдебиеттер:
Негізгі:
1. Темірғалиев Н. ” Математикалық анализ, І т, Алматы 1987
2. Фихтенгольң г. т “Математикалық анализ негіздері, ” І т Москва 2003
қосымша:
1. Н. С. Пискунов, Дифференциальное и интегральное исчесления І, ІІ том, Москва, 1988 г.
2. В. П. Минорский, «Сборник задач по высшей матеамтике», Москва, «Наука» 1987 г.
- Ортогональ функциялар.
Анықтама : Егер
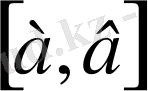 сегменетте интегралданушы f(х) және
сегменетте интегралданушы f(х) және
 (х) функциялар көбейтіндісінен алынған интеграл нөлге тең болса, оларға өзара ортогональ сызық қиялар делінеді.
(х) функциялар көбейтіндісінен алынған интеграл нөлге тең болса, оларға өзара ортогональ сызық қиялар делінеді.
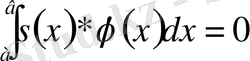 (1)
(1)
Мысал:
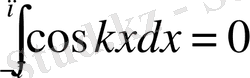
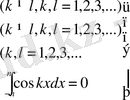 (2)
(2)
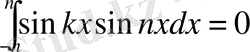
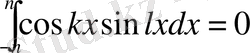
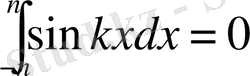
2. Периоды 2l- ге тең болған функцияны Фурье қатарына жіктеу.
Егер
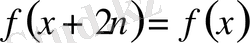 болса оның фурье қатарына жіктеуі жалпы түрде былай жазылады:
болса оның фурье қатарына жіктеуі жалпы түрде былай жазылады:
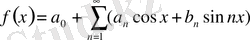 (3)
(3)
Енді а 0 , а п және в п коефиценттерін f(х) арқылы табайық
(3) ні
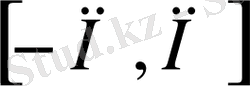 аралығында интегралдасақ
аралығында интегралдасақ
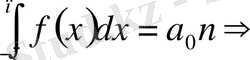
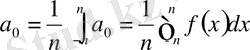 (4)
(4)
(3) ні cos kx -қа көбейтіп [-n, n] аралығында интегралдаймыз.
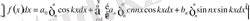
(2) формулаға сәйкес
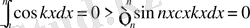
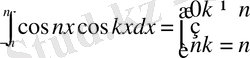 ді табамыз
ді табамыз
Сонда па
к
=
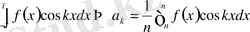 Equation. 3 (5) болады
Equation. 3 (5) болады
Осы жолмен (3) ті sin kx қа көбейтіп [-n, n] интегралды интервалдасақ
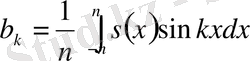 табамыз
табамыз
Қортынды :Егер а ( ч+2т) =f(x) болса ол[-n, n] сегментте Фурье қатарына жіктеледі. . Қатардың а 0 , а к , в к коэфиценттері мына формулр ррқылы есептеледі.
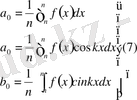
Ескерту: 1 Егер f(-х) =-(х) болса а 0 =0; а к =0 болып в к ны есептеу керек. Яғни f(x) тек синустар бойынша фурье қатарына жіктеледі .
Ескерту: 2 Егер f(-х) =-(х) болса в к =0 болып а 0 , а к -ларды есептеу керек.
Мысал:1 f(x) =x f(x+2n) =f(x) болсын
а(-x) = -f(x) сандықтан a 0 =a k =0
b
k
=
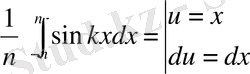 Equation. 3
Equation. 3
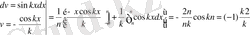 Equation. 3
Equation. 3
x=+2
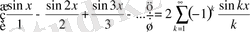 Equation. 3
Equation. 3
Жауап: x=2
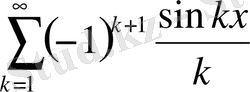 Equation. 3
Equation. 3
у
f(x) =x тың графигі
-3п -2п -п
-х п 2п 3п х
0
-п
-у
2. f(x) =x 2 f(-x) =f(x) сондықтан в к =0 болады
а
0
=
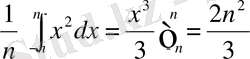
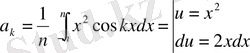
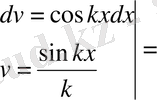
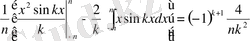
Жауап:
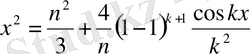 n
2
у
n
2
у
f(x) =x 2 тың графигі
-x
-3n -2n -n 0 n 2n 3n x
-y
3. Периоды 2 l-ге тең болған функцияны Фурье қатарына жіктеу .
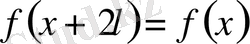 Equation. 3,
Equation. 3,
 Equation. 3 болсын. Сонда
Equation. 3 болсын. Сонда
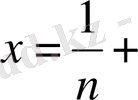 деп алсақ
деп алсақ
x=-1 болғанда t=-n; x=1 болғанда t=+n болады, яғни
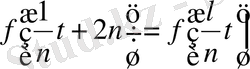 болады.
болады.
Сонда
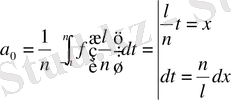
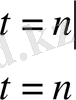
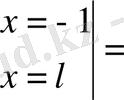
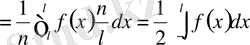
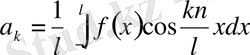
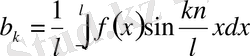
Мысал f(x) =x+2 f(x+6) =f(x) 2l=6 l=3
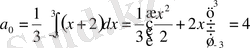
a k =0;
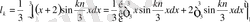
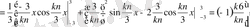
Жауабы:
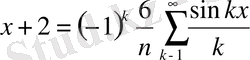
- Периодсыз функцияны Фурье қатарына жіктеу
Егер шегараланған f(x) функция [0, l] үздіксіз немесе шекті ретті біріеші тип үзілістерге ие болса оны фуре қатарына жіктеуге болады . Бұнын үшін f(x) ты [-1, l] интервалды тақ деп алсақ синустарға жұп деп алсақ косинустарға жіктеуге болады.
Мысал: [0, n] интервалда берілген
функция косинустар бойынша жіктелсін
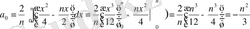

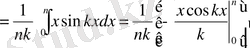
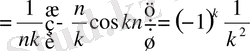
Жауап:
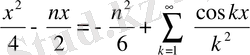
Геометрияның кеңістіктегі фигураларды зерттейтін бөлімі - стереометрия
Стереометрия бөліміндеде планиметрия сияқты фигуралар қасиеті теоремаларды дәлелдеу арқылы тағайындалады. Кеңістіктің негізгі элементтері: нүкте, түзу және жазықтық.
Кеңістіктегі жазықтықтардың негізгі қасиеттері:
С1. Кез келген жазықтыққа тиісті және тиісті емес нүктелер бар болады.
С2. Егер кез келген екі жазықтықтың ортақ нүктелері бар болса, онда екі жазықтық осы нүкте арқылы өтетін түзу бойымен қиылысады.
С3. Егер екі түзу бірнүктеде қиылысатын болса, онда олар арқылы тек бір ғана жазықтық жүргізуге болады.
Кеңістіктегі жазықтықтардың және түзулердің параллелдігі.
Бір жазықтықта жататын екі түзудің ортақ нүктесі болмаса олар параллел болады.
Т1. Берілген түзудің бойында жатпайтын нүкте арқылы осы түзуге параллель тек бір ғана түзу жүргізуге болады.
Т2 . Параллель екі түзудің біреуіне үшінші түзу параллель болса, онда үш түзу бір-біріне параллель болады. .
ТЗ . Егер жазықтықта жатпайтын түзу осы жазықтықтағы бір түзуге параллель болса, онда түзу жазықтыққада параллель болады.
Т4. Егер бір жазықтықта жататын қиылысатын екі түзу сәйкесінше екінші жазықтықта жататын қиылысатын екі түзуге параллель болса, онда жазықтықтарда параллель болады.
Т5. Жазықтықтан тысқары алынған нүкте арқылы берілген жазықтыққа параллель бір ғана жазықтық жүргізуге болады
Кеңістіктегі жазықтықтардың және түзулердің перпендикулярлығы.
Егер екі түзу тікбұрыш жасап қиылысатын болса, онда олар перпендикуляр түзулер болады.
Т1. Егер қиылысатын екі түзу сәйкесінше тікбұрыш жасап қиылысатын екі түзуге параллель болса, онда оларда перпендикуляр түзу болады. .
Т2 . Егер түзу бір жазықтықта жататын қиылысатын екі түзуге перпендикуляр болса, онда жазықтыққа да перпендикуляр болады.
ТЗ . Егер жазықтық параллель екі түзудің біреуіне перпендикуляр болса, онда жазықтық екіншісінеде перпендикуляр болады.
Т4. Егер екі түзу бір жазықтыққа перпендикуляр болса, онда олар параллель болады.
Т5. Егер жазықтық екінші жазықтықа перпендикуляр түзу арқылы жүргізілетін болса, онда ол жазықтықтар өзара перпендикуляр болады.
Көпжақтар. Көпжақтардың бет аудандары және көлемі.
Көпжақ - саны шекті дөңес көпбұрыштардан тұратын фигура
Көлбеу призма
көлемі
V=S
пқ
a
, мұндағы
S
пқ
- перпендикуляр қима ауданы
a
-бүйір қабырға. .
Көлбеу призманың бүйірбеті
S
п. қ
=P
п. қ
a
, мұндағы
P
пқ
-перпендикуляр қима периметрі
a-
бүйірқабырға
.
Көлбеу призманың толық беті
S
т. б
=S
б
+2S
таб
, мұндағы
S
б
, - көлбеу призманың бүйір беті.
S
табн
- табанының ауданы.
Тік призма көлемі V=S таб a , мұндағы S таб - тік призманың табанының ауданы, a - бүйір қыры.
Тік призманың бүйірбеті S б. б =P таб a , мұндағы, P таб -призманың табанының периметрі,
Тік призманың толық беті S т. б =S б. б +2S таб , мұндағы S б. б - призманың бүйірбеті, S осн - призманың табанының ауданы.
Егер призма табаны параллелограмм болса, онда ол параллелепипед деп аталады
Параллелепипедтің табаны тікбұрышты болса, онда оны тікбұрышты параллелепипед деп атаймыз.
Тікбұрышты параллелепипед көлемі V=abc , мұндағы a, b, c - параллелепипед өлшемдері
Тікбұрышты параллелепипед бүйірбеті
S
б
=2c(a+b)
, мұндағы
a, b
-табан өлшемдері,
c
- тікбұрышты параллелепипедтің бүйір қабырғасы.
Тікбұрышты параллелепипед толықбеті
S
т. б
=2(ab+bc+ac)
, мұндағы
a, b, c
- параллелепипед өлшемдері .
Пирамида көлемі
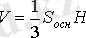 мұндағы
S
таб
- табанының ауданы,
H
-биіктігі.
мұндағы
S
таб
- табанының ауданы,
H
-биіктігі.
Толық беті
S
т. б
=S
б
+S
таб
,
S
б
- бүйір бетінің ауданы,
S
таб
- табанының ауданы.
Қиық пирамида көлемі
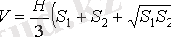
мұндағы
S
1
, S
2
- қиық пирамиданың табанының аудандары,
H
-биіктігі.
.
Қиық пирамида толық беті
S
т
=S
б
+S
1
+S
2
,
мұндағы
S
б
- қиық пирамиданың бүйір бетінің ауданы,
S
1
, S
2
- қиық пирамиданың табанының аудандары.
1. Егер пирамидаға төмендегі екі шарттың бірі орындалса:
а) барлық бүйір жақтары табан жазықтығымен бірдей бұрыш жасайды;
б) барлық бүйір жақтарының апофемасының ұзындықтары бірдей; Онда пирамиданың төбесінің проекциясы табанына іштей сызылған шеңбердің центрімен беттеседі.
2. Егер пирамидаға төмендегі екі шарттың бірі орындалса:
а) барлық бүйір қырлары табан жазықтығымен бірдей бұрыш жасайды;
б) барлық бүйір қырлары ұзындықтары бірдей;
Онда пирамиданың төбесінің проекциясы табанына сыттай сызылған шеңбердің центрімен беттеседі.
3. Егер үшжақты бұрыштың, екі сүйір жазық бұрышы тең болса, онда олардың ортақ қабырғаларының проекциясы үшінші жазық бұрыштың биссектрисасы болады.
4. Егер пирамиданың табаны тікбұрышты үшбұрыш болса, онда пирамиданың биіктігінің табаны, табанына сырттай сызылған шеңбердің центрімен беттеседі.
Мысалдар:
- Дұрыс төртбұрышты пирамиданың биіктігі 7 см, табан қабырғасы 8см. Бүйір қабырғасын табыңыз.
Берілгені: SABCD - дұрыс төртбұрышты пирамида. SO = h = 7 см; AB=BC=CD= =DA=8 см.
Табу керек: l=AS=BS=CS=DS
Шешуі:: ABCD - квадрат
AC 2 = AD 2 + CD 2 = 64 + 64 = 128; AC =
=8
;
∆SOC - тікбұрышты,
l=SC=
=
=
=
=9
Жауабы: 9 см.
2. Тікбұрышты параллелепипедтің үш өлшемі берілген; 2см, 3см және 6см
Параллелепипед диагоналын табыңыз.
Берілгені: ABCDA 1 B 1 C 1 D 1 - тікбұрышты параллелепипед;
a=2 см, b=3 см, с=6 см.
Табу керек: d=D 1 B
Шешуі:
d 2 =a 2 +b 2 +c 2 ;
d=
=7 см,
Жауабы: d=7 см.
3. Пирамиданың табанына параллель жазықтық биіктікті 1:1 қатынасындай бөледі. Егер табан ауданы 60м 2 болса, қиманың ауданын табыңыз.
Берілгені: ABCDA 1 B 1 C 1 D 1 - қиық пирамида,
SO 1 : O 1 O = 1:1
(ABCD) (A 1 B 1 C 1 D 1 ) ; S=S ABCD =60 м 2
Табу керек: SA 1 B 1 C 1 D 1 =SO 1 =h; SO=2h
Шешіуі: SO 1 2 :SO 2 =S 1 :S;
=
; S 1 =
=15 м 2
Жауабы: S=15 м 2
4. Сүйір бұрышы 30 о тікбұрышты ұшбұрышты сырттай сызылған шеңбердің центріне ұзындығы 6см биіктік тұрғызылған, үшбұрыш жазықтығына тиісті емес ұшынан үлкен катетке дейінгі қашықтық 10см. Ұшбұрыш гипотенузасын табыңыз.
Берілгені :шеңбер, (центр О), OB=OC=OA=R, ∆ABC - тікбұрышты.
... жалғасыС=90 о , B=30 o , DO┴S, DO=6 см, DM┴CB, DM=10 см,
Табу керек: AB
Шешуі: Үш перпендикуляр теоремасы бойынша: OM┴CB=>MOCA. OB=OC=OA=R, онда O - ортасы AB, => MO= ½ AC=R/12, AC=AB*sin 30 o =R ∆DOM-тікбұрышты, демек MO 2 =MD 2 -OD 2 =100-36=64, MO=8, AC=16, AB=2AC=32 см.
Жауабы: 32 см.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz