Түйіндес операторлар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Қазақстан Республикасы Білім және Ғылым Министрлігі

Семей қаласы Шәкәрім атындағы Мемлекеттік Университеті

СӨЖ

Тақырыбы: Түйіндес операторлар

Семей

Егер гильберт кеңістігі Н-та анықталған сызықтық операторларды қарастырсақ, онда нақты жағдайда Н пен Н ^/ бірдей болатындықтан және ондағы элементтердің скаляр көбейтіндісі болатынын пайдаланып, айрықша қасиетті симметриясы бар (немесе) өзі түйіндестік қасиеті деп аталатын операторлар класын ажыратуға болады және осы класстың операторларын еркін банах кеңістігінде берілген еркін сызықтық операторларға қарағанда тереңірек зерттеу керек.

Н - комплекс гильберт кеңістігі және t Н-та анықталған және осы кеңістіктегі мәндерге ие болатын шектеулі сызықтық оператор болсын делік. Н-та берілген скаляр көбейтінді бойынша t-ға түйіндес t* операторын барлық үшін

(1)

теңдігі бойынша анықтаймыз.

1-анықтама. Сызықтық шектеулі t операторы егер

(2)

болса, онда шектеулі өзі түйіндес (немесе Эрмит симметриялы) оператор деп аталады.

Мысалдар. 1. дегі ядросы Фредгольм операторына түйіндес оператор болып ядросы болатын Фредгольм операторы болып есептеледі. Өзі түйіндестік шартының түрі Нақты ядро жағдайында бұл шарт симметриялық шартына көшеді.

2. дегі әрбір функциясына функциясына сәйкес қоятын t операторын құрайық. Бұл оператор өзі түйіндес екеніне көз жеткізу қиын емес.

Бұдан әрі «шектеулі» деген сөзді біз қалдырып кетеміз. Алдыңғыдан, егер t - өзі түйіндес оператор және α-нақты сан болса, онда αt-да өзі түйіндес оператор, және егер t мен u - өзі түйіндес операторлар болса, онда u+t - өзі түйіндес, ал tu сонда, тек сонда ғана өзі түйіндес, егер t мен u операторы ауыстырымды болса. Ең соңында, егер бірқалыпты немесе күшті операорлық топология мағынасында жинақты болса, онда t-да өзі түйіндес оператор болады.

Егер ті х бойынша және у бойынша функционал болса, мұнда t - өзі түйіндес оператор, онда біз деп белгілейтін осы функционал келесі шарттарды қанағаттандыратын көру қиын емес:

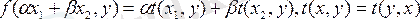
Ондай функционалды біз бисызықты Эрмит формасы деп атаймыз. Бұл форма мағынасында шектеулі, мұнда С _t - кейбір тұрақты (қарастырған жағдайда ) .

Сонымен, әрбір өзі түйіндес t операторы кейбір шектеулі бисызықты Эрмит формасын тудырады.

Керісінше, егер шектеулі бисызықты Эрмит формасы берілсе, онда ол теңдігін қанағаттандыратын кейбір өзі түйіндес t операторын тудырады.

Іс жүзінде, формасында у элементін белгілеп, біз х-тен сызықтық функционал аламыз. Сонымен мұнда у ^/ элементі бірмәнді анықталады. Сонда, біз теңдігімен анықталатын және болатындай t операторын аламыз. t - сызықтық оператор екені айқын. t - шектеулі оператор екеніне оңай көз жеткізуге болады. Расында да

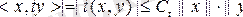
деп және ке қысқартып екенін табамыз. t - өзі түйіндес оператор екенін көрсетеміз. Кез келген үшін

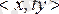
бұдан және екені шығады.

Енді бисызықты Эрмит формасын аламыз және онда делік. Барлық х-тер үшін нақты мәндер алып

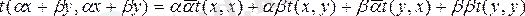
болатындай квадрат формасын аламыз. Сондай формасын бисызықты Эрмит формасына сәйкес квадраттық Эрмит формасы деп атаймыз. Егер бисызықты Эрмит формасы берілсе, онда сол арқылы сәйкес квадраттық Эрмит формасы беріледі. Кері жағдай да ақиқат, квдарттық Эрмит формасы берілуі бисызықты Эрмит формасын бірмәнді анықтайды. Бұл бисызықты форма келесі теңдікпен анықталады (полярлау принципі)

(3)

мұнда және

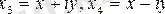
Квадраттық Эрмит формасы сонда, тек сонда ғана шектеулі болады, яғни егер сәйкес бисызықты форма шектеулі болса ғана екенін көрсету қиын емес. формасы үшін полярлық деп аталады.

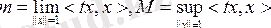
болсын делік. m және М сандары өзі түйіндес t операторының төменгі және жоғарғы шекарасы деп аталады.

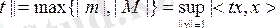
екенін көрсетейік.

Іс жүзінде, болсын делік. Сонда

(4)

және сондықтан

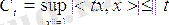
Басқа жағынан, кез келген үшін болады. Сондықтан, егер z Н-тағы нөлден ерекше элемент болса, онда

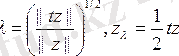
де

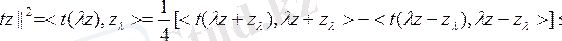
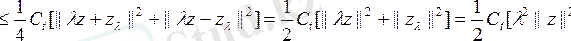
екенін аламыз, бұдан және содан

(5)

(4) және (5) теңсіздіктерінен керекті теңдікті аламыз. Дәлелденген бойынша, жеке жағдайда, егер барлық үшін өзі түйіндес t мен u операторлары теңдігі орындалса, онда