Регрессиялық модель параметрлерін статистикалық бағалау және гипотезаларды тексеру


Тақырыб 3: Регрессиялық модельдің параметрлерін анықтау. Параметрлерді статистикалық бағалау, гипотезаларды тексеру
- Кездейсоқ шама дегеніміз не?Мүмкін болатын мәндер жиынтығынан кездейсоқ қандай да бір мән алынады, солкездейсоқ шамадеп аталады. Тәжірибенің нәтижесінде әртүрлі мән қабылдай алатын шаманыкездейсоқ шамадеп атайды.
- Кездейсоқ шамалардың түрлері?Дискретті және үздіксіз кездейсоқ шамалар (дискретті-үзікті) x кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда ондай кездейсоқ шаманыдискреттідеп атайды (үзікті шама) . Егер x кездейсоқ шамасы шекті немесе шексіз интервалдың барлық мәндерін қабылдайтын болса, оныүздіксізкездейсоқ шама деп атайды.
- Генеральды жиынтық (совокупность) дегеніміз не?Кездейсоқ шамалардың барлық мүмкін мәндерінің толық жиынтығы -генеральды жиынтықдеп аталады. Математикалық күтімді осымен есептейміз.
- Кездейсоқ таңдама (выборка) дегеніміз не?Зерттеу үшін генеральды жиынтықтан кездейсоқ іріктелген объектілер жиынтығы -кездейсоқ таңдамадеп аталады.
- Қандай таңдама репрезентативтік деп аталады?Генеральды жиынтықтың негізгі заңдылығын, сипаттамасын толық, дұрыс көрсететін таңдамарепрезантивті таңдамаболып табылады. Алынған таңдама бойынша генеральды жиынтықты дұрыс сипаттау үшін таңдама репрезентативті болуы керек.
- Кездейсоқ шаманың таралу заңы, таралу функциясы және таралу тығыздығы деп нені атаймыз?Кездейсоқ шаманы толық сипаттайтын шама оныңтаралу функциясыболып табылады. Таралу функциясы график түрінде немесе кездейсоқ шаманың ықтималдылығы мен шаманың мәндері арасындағы байланыс түрінде көрсетіледі. Дискреттік таралу заңдары. Дискреттік кездейсоқ шаманың таралу заңы (искреттік таралу заңы) келесі тәсілдердің біреуімен берілуі мүмкін:
- аналитикалық - кездейсоқ шаманың мәніне ықтималдықтың тәуелділігін бейнелейтін математикалық өрнек түрінде;
- кестелік - кездейсоқ шаманың мүмкін болатын мәндері және оларға сәйкес ықтималдықтар санақталған кездейсоқ шаманың таралу қатары түрінде;
- графикалық - абсциссалар өсі бойынша кездейсоқ шаманың мүмкін болатын мәндері, ал ординат өсі бойынша сол мәндердің ықтималдықтары салынған таралу көпбұрышы түрінде
- Математикалық күтім дегеніміз не және ол нені сипаттайды?Математикалық күтім- біздің алған есептеуіміздің арифметикалық ортасы. Оны алгебралық түрде есептесек, орташа мән шығады. Осы шыққан мән кездейсоқ шама.
- Дисперсия дегеніміз не және ол нені сипаттайды?Дисперсия- біз күткен сан мен практикадағы кездейсоқ санның айырмасы, яғни кездейсоқ санның математикалық күтімнен ауытқуы.
- Орташа квадратты ауытқу (стандарт) дегеніміз не және ол нені сипаттайды? Егер дисперсияны түбір астына алса, орташа квадраттық ауытқушығады. Яғни, алдымен орташа мән есептеледі, содан кейін әрбір бастапқы және орташа мән арасындағы айырмашылық алынады, квадратқа салынып, қосылады, содан кейін берілген жиынтықтағы мәндер санына бөлінеді.
- Корреляцияның коэффициенті дегеніміз не және ол нені сипаттайды?Корреляция- кездейсоқ факторлардың байланысы
Корреляциялық талдау х және у екі айнымалының өзара байланыс дәрежесін қарастырады. Корреляция коэффициенті −1-ден +1 -ге дейінгі мәндерді қабылдай алады. Егер модуль 1-ге жақын болса, онда бұл күшті байланыстың болуын білдіреді, ал 0-ге жақын болса, байланыс әлсіз немесе мүлдем жоқ.
- Кездейсоқ шаманың қандай бағасы бақуатты (состоятельная), жылжымаған болып табылады?
Математикалық статистикадағы бақуатты бағалау- бұл бағаланатын параметрге ықтималдықпен сәйкес келетін нүктелік бағалау. Математикалық статистикадағы жылжымаған бағалау-бұл математикалық күту бағаланатын параметрге тең болатын нүктелік бағалау.
Таралу параметрлердің статистикалық бағасы.
Кездейсоқ шаманың таралуының негізгі параметрлерінің бақуатты (состоятельные) және жылжымаған (несмещенные) бағалары (математикалық күтім M
X
және дисперсия σ
Х
2
) келесі формулалар бойынша табылуы мүмкін:
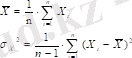
- Сенімді ықтималдық, маңыздылық деңгейі дегеніміз не?
Сенімділік интервалымен байланысқан ықтималдылық сенімділік ықтималдығы деп аталады. Егер сенімді аралық 95% деңгей бойынша құрылса, онда тиісті сенімді ықтималдық 5% немесе 0, 05 болады, 98% деңгей бойынша интервал үшін - 2% немесе 0, 02 және т. б.
Маңыздылық деңгейі -бұл айырмашылықтарды маңызды деп санайтын ықтималдық, ал олар кездейсоқ. Сонымен, маңыздылық деңгейі ықтималдықпен айналысады. Маңыздылық деңгейі сынамалар арасындағы анықталған айырмашылықтардың сенімділік дәрежесін көрсетеді, яғни айырмашылықтар шынымен бар екеніне қаншалықты сене алатынымызды көрсетеді.
- Еркіндік дәрежесі дегеніміз не және ол қалай анықталады?
Математикалық статистикада еркіндік дәрежелерінің саны -бұл статистикалық сипаттаманы есептеу кезінде қолданылатын мәндердің саны, олар еркін өзгеруі мүмкін. Бұл бүтін теріс емес сан. Статистикалық сипаттамаларды бағалау әртүрлі деректер көлемінде жүргізілуі мүмкін.
- Сенімді аралық, сенімді шекаралар дегеніміз не? θ арқылы бізді қызықтыратын параметрдің бағасын белгілейік. Онда бағаның дұрыстығы мен дәлдігін анықтау есебі параметрдің белгісіз ақиқат мәні 1-α (α - 0. 1, 0. 05, 0. 01 … тең, жеткілікті аз шама) ықтималдықпен θ параметрін қамтитын (θ1, θ2) аралығында жатады деп тұжырымдауға болатындай аралықты анықтауға келтіріледі. (θ1, θ2) аралықты -сенімді аралығы(доверительный интервал) деп, ал 1-α ықтималдықты -сенімді ықтималдығы(доверительная вероятность) деп атайды. Қысқаша айтқанда, сенімді аралық- тәжірибеде өлшенген сенімділік ықтималдылығына сәйкес келетін мәндер түсетін аралық. Сенімді шекара- сенімділік аралығының шекаралық нүктелері.
- Математикалық күтім үшін сенімді аралық қалай анықталады? Mx үшін сенімді аралық келесідей:Есепте х орташа боп тұр. бұл жерде, t(α, ν) -ны ықтималдығы α және еркіндік дәрежелері ν=n-1 бойынша Стьюденттің таралу кестесінен анықтайды
- Дисперсия үшін сенімді аралық қалай анықталады? Сондықтан, 1-α сенімді ықтималдыққа сәйкесдисперсия үшін сенімді аралық:Есепте х дисперсия боп тұр. χ2(1-α/2, v) =(n-1) ·σX2/σ22шаманы Пирсонның таралу кестесі бойынша ықтималдығы 1-α/2 және еркіндік дәрежелер v=n-1 санында табады, ал χ2(α/2, v) =(n-1) ·σX2/σ2-ді ықтималдығы α/2 және еркіндік дәрежелер v=n-1 -де анықтайды.
- Статистикалық гипотеза дегеніміз не? Статистикалық гипотеза түсінігі кездейсоқ шаманың таралу түрі немесе оның таралуының кейбір параметрі туралы жорамалдауды білдіреді. Гипотезаны тексерудің мағынасы берілген сұрыптау бойынша есептелген белгілі бір статистикалық көрсеткішті (мағыналық критерийін) тексерілетін гипотеза дұрыс болатын шартта теориялық табылған мағыналық критериймен салыстыруда.
- Математикалық күтімнің С санына тең болуы жөніндегі гипотеза. Mx= C деген гипотезаны тексеруде критерий ретінде мынадай шаманы пайдаланады:
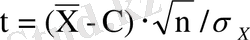 (3. 9)
(3. 9)
Гипотеза дұрыс деген шартта бұл шама еркіндік дәрежелері v=n-1 болатын Стьюденттің t-таралуына ие. Егер (3. 9) қатынасы бойынша есептелген t мәнінің абсолют шамасы маңыздық деңгейі α және еркіндік дәрежелер саны ν болғандағы t-таралу кестесі бойынша табылған критикалық t кр =t(α, v) мәнінен аспаса, онда M x =C гипотезасы қабылданады, керісінше жағдайда ол қабылданбайды.
- Екі кездейсоқ шамалардың математикалық күтімдерінің бір біріне тең болуы жөніндегі гипотеза. X және Y кездейсоқ шамалардың көлемдері n1және n2болатын екі таңдамалар бойынша есептелгенекі математикалық күтімдердің бір біріне тең Mx=Myекендігі жөніндегі гипотезаны тексеруді келесі критерий бойынша жүргізеді: t =) /σX-Y(3. 10) . t критериі еркіндік дәрежелер саны v=n1+n2-2 болатын Стьюденттің t-таралуына ие. Гипотезаны алдыңғы жағдайдағыдай тексереді, демек t<tкрболғанда гипотеза қабылданады, ал t>tкр қабылданбайды.
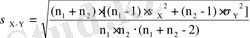
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz