Электр зарядтар мен электростатика: Кулон заңы, электр өрісі, электростатикалық индукция және Остроградский-Гаусс теоремасы


ЭЛЕКТР ЗАРЯДТАР
Тірек ұғымдар және негiзгi сiлтемелер: электростатика, электр заряды, эбонит, электрон, протон, электр өткізгіш, изоляторлар, диэлектриктер.
Электростатика тыныш тұрған электр зарядты денелердің өзара әсері және қасиеттерін үйренетін электр курсы бөлімі болып саналады.
Қарапайым тәжірибелер жәрдемінде табиғатта электр зарядының екі түрі бар екендігі анықталған. Мысалы, шыны таяқшаны жібекке немесе теріге үйкелгенде таяқшада оң зарядтар пайда болады, эбонит таяқшаны жүнге үйкелгенде теріс зарядтар пайда болады.
Бірдей таңбалы зарядтар мен зарядталған денелер бір-бірінен тебіледі, таңбасы әр түрлі болған зарядтар мен зарядталған денелер бір-біріне тартылады.
Сонымен, әр түрлі заттан құралған екі дене бір-біріне үйкелсе, олар зарядталады. Бір денені екінші денеге тигізу жолы мен электр зарядын ұзату мүмкін.
Бірқанша тәжірибелер жәрдемінде анықталғанындай, әр қандай зарядталған дене заряды белгілі бір бүтін элементар зарядтар санына тең болады. Бір элементар зарядтың мәні 1, 6⋅10 -19 Кл ға тең.
Теріс зарядқа ие болған ең кіші бөлшек электрон деп аталады.
Оң зарядқа ие болған ең кіші бөлшекке протон деп аталады.
Заттар өткізгіш және диэлектриктерге бөлінеді. Егер денедегі электр зарядтар еркін орын ауыстырса, мұндай денелер электр өткізгіш деп аталады. Белгілі бір денелерде электр зарядтар орын ауыстырмайды, сол үшін мұндай денелер изоляторлар немесе диэлектриктер деп аталады.
Өткізгіштерге барлық металлдар, тұздар, қышқылдардың ерітінділері, қыздырылған газдар және басқа заттар кіреді.
Диэлектриктерге шыны, каучук, эбонит, май және басқа заттар жатады.
Әр түрлі заттан құралған денелер үйкеліс нәтижесінде оларда әр түрлі таңбалы электр зарядтар пайда болады. Мысалы, металлды эбонитке үйкесек, металлда оң зарядтар, эбонитте болса теріс зарядтар пайда болады.
Зарядталмаған денелерде мөлшері бойынша тең, қарама-қарсы таңбалы электр зарядтар бар, сол үшін олар бір-бірін компенсациялайды. Егер денеде артықша оң зарядтар болса, дене оң зарядталған, артықша теріс зарядтар бар болған жағдайда дене теріс зарядталған болады.
Зарядталған денеге басқа зарядталмаған денені тигізсек, бұл денелерде электр зарядтар қайта бөлінеді, яғни бірінде артықша оң зарядтар, екіншісінде болса сонша артықша теріс заряд пайда болады.
Бұл тәжірибелер мен бекітілген табиғат заңдарынан бірі электр зарядтың сақталу заңы, яғни электр жағынан тұйық жүйені құраған денелердің электр зарядтарының алгебралық жиындысы тұрақты болады.
Бақылау сұрақтары:
1. Электростатика деп нені айтады?
2. Электр заряды дегенде нені түсінесіз?
3. Эбонит таяқшаның қасиеті неде?
4. Электрон деген не?
5. Протон деген не?
6. Денелердің электр өткізгіштігін не сипаттайды?
7. Изоляторлар деген не?
8. Электр зарядының сақталу заңы қашан орындалады?
КУЛОН ЗАҢЫ
Тірек ұғымдар және негiзгi сiлтемелер: электр заряд, Кулон заңы, бұралмалы диномометр, цилиндр, пропорционалдық коэффициентi, Ампер.
Электр зарядтарының өзара әсер заңын Ш. Кулон 1785-жылы тәжірибе жолы мен анықтаған. Зарядталған денелердің өзара әсерін Кулон бұралмалы диномометр де үйренген. Бұралмалы диномометр (1-сурет) төмендегі бөліктерден құралған: екі әр түрлі радиусты бір-біріне бекітілген шыны цилиндрлерден ( A , V ), цилиндрдің ( V ) бас бөлігінде айналатын құрылғы ( M ) орналастырылған және оған серпімді сым бекітілген. Сымның төменгі бөлігіне изоляторлы жеңіл таяқша ( D ) тепе-теңдік күйінде орналастырылған. Таяқшаның бір ұшында n металл шар, екінші жағында ( S ) дене орналастырылған. Үлкен цилиндрдің саңылауынан изоляциялы заттан жасалған таяқша жәрдемінде металл m шар түсіріледі. Айналатын ( M ) құрылғыда градус шкалалары бар (оның қандай бұрышқа бұрылғанын анықтау мүмкін) . Дәл осындай градус шкалалары цилиндрдің сыртында да бар.
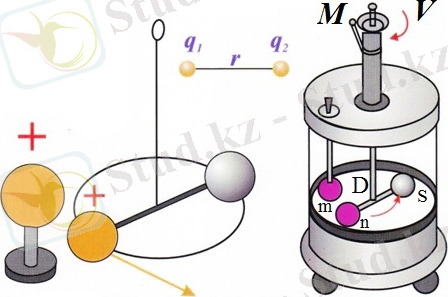
1- сурет
Кулон тәжірибені төмендегідей өткізген:
1. n және m металл шарларға (ортасындағы қашықтықты өзгертірмей сақтаған күйде) q 1 және q 2 бірдей таңбалы заряд мөлшері берілгенде, олар ортасындағы тебіліс күштерін сымға асылған таяқшаның белгілі бұрышқа бұрылуына қарап анықтаған (мұнда сымның бұрылу моменті бұрылу бұрышына пропорционал және тұрақты иін болғанда күш моменті күшке пропорционал болады) .
2. Зарядталған металл шарларды әр түрлі қашықтықтарда орналастырып, сымның бұрылуына қарап тебіліс күштерінің мәнін анықтаған. Кулон шарлардағы заряд мөлшерін өзгертудің қарапайым әдісін тапқан: ол зарядсыз шарды зарядталған шарға (шарлар бірдей болуы керек) тигізілгенде, зарядтар шарларда тең таралады, яғни
m
шардағы заряд мөлшерін
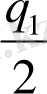 ,
,
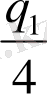 ге және т. б. кемейту мүмкін.
ге және т. б. кемейту мүмкін.
Әр түрлі таңбалы зарядтар шарларға берілгенде, бұл шарлар арасында өзара тартылыс күштері пайда болады. Зарядталған денелердің өзара әсер күшi бұл денелер арасындағы ортаның қасиеттеріне байланысты.
Өткізілген тәжірибелерге негізделіп Шарль Кулон төмендегі заңды анықтады: екі нүктелік зарядталған денелердің өзара әсер күшi, осы зарядтардың көбейтіндісіне тура пропорционал және олар арасындағы қашықтықтың квадратына кері пропорционал.
Зарядтардың өзара әсер күшi тең және зарядтарды бірлестіретін түзу сызық бойымен бағытталған. Шарлардағы зарядтарды q 1 және q 2 мен, олар арасындағы қашықтықты r мен белгілесек, Кулон заңы:
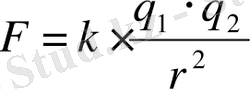 2. 1.
2. 1.
көрінісінде жазылады, бұл жерде,
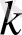 - пропорционалдық коэффициентi, оның мәні қандай бірліктер жүйесінде алынғандығына байланысты.
- пропорционалдық коэффициентi, оның мәні қандай бірліктер жүйесінде алынғандығына байланысты.
Бірер ортада зарядтардың өзара әсер күшi төмендегіге тең болады:
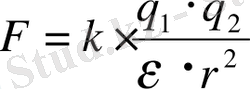 2. 2.
2. 2.
бұл жерде, ε - өлшеусіз шама болып, ортаның салыстырмалы диэлектрик өтімділігі деп аталады және ол ортаның электр қасиеттерін сипаттайды, вакуум үшін ε =1.
(2. 1. ), (2. 2. ) көрінісіндегі Кулон заңы тек қозғалмайтын нүктелік электр зарядтардың өзара әсері үшін орынды. Нүктелік заряд деп сондай зарядталған денеге айтылады, оның сызықты өлшемдерінің басқа зарядталған денелерге дейін болған қашықтыққа қатынасы есепке алынбайды.
Халықаралық бірліктер жүйесінде ( СИ ) электр зарядының бірлігі етіп Кулон ( Кл ) қабылданған. 1 Кулон ( Кл ) деп өткізгіштегі ток 1 Амперге тең болғанда 1 секунд уақыт ішінде өткізгіштің көлденең қимасының ауданынан өтетін заряд мөлшеріне айтылады.
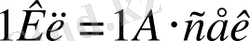
Кулон заңы
ХБ
жүйесінде өрнектелгенде ондағы
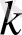 коэффициент
коэффициент
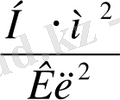 пен өлшенеді. Бұл коэффициенттің сан мәнін тәжірибеде анықтау мүмкін. Бұл үшін бір-бірінен
r
=1
m
қашықтықта тұрған екі
q
1
=
q
2
=1 Кл заряд арасындағы өзара әсер күшін Ньютондарда өлшеп, (2. 1. ) формуладан пайдаланып есептегенде
пен өлшенеді. Бұл коэффициенттің сан мәнін тәжірибеде анықтау мүмкін. Бұл үшін бір-бірінен
r
=1
m
қашықтықта тұрған екі
q
1
=
q
2
=1 Кл заряд арасындағы өзара әсер күшін Ньютондарда өлшеп, (2. 1. ) формуладан пайдаланып есептегенде
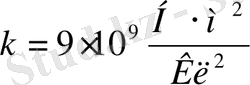 болады. (2. 1. ), (2. 2. ) формулалардан
болады. (2. 1. ), (2. 2. ) формулалардан
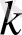 коэффициент
ХБ
жүйесінде төмендегіге тең болады:
коэффициент
ХБ
жүйесінде төмендегіге тең болады:
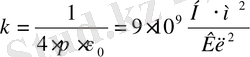 2. 3.
2. 3.
бұл жерде, ε 0 - электр тұрақтысы деп аталады, оның сандық мәні төмендегіге тең:
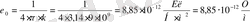 2. 4.
2. 4.
(2. 3. ) ті есепке алып, Кулон заңы
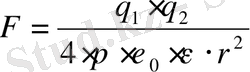 2. 5.
2. 5.
көрінісінде жазылады.
ЭЛЕКТР ӨРІС. ЭЛЕКТР ӨРІС КЕРНЕУЛІГІ ЖӘНЕ ОНЫҢ СЫЗЫҚТАРЫ
Тірек ұғымдар және негiзгi сiлтемелер: электр өріс, электр өріс кернеулігі, электростатикалық өріс, стационар, алыстан әсер, жақыннан әсер, шекті жылдамдық, электрод.
Әр қандай зарядталған денелер айналасында (кеңістікте) электр өріс пайда болады. Егер зарядталған денелер қозғалмайтын болса, оның айналасында пайда болатын өріс электростатикалық өріс деп аталады, яғни уақыт барысында өзгермейді (стационар) .
Электр өріс электрoмагнит өрістің жеке күйі болып, осы өріс арқылы зарядталған денелер өзара әсерлеседі.
Зарядталған денелер өзінің айналасында белгілі бір өзгерістерді жүзеге келтіреді, мысалы, басқа зарядталған дене жақындаса оған әсер ететін күштер пайда болады. Егер кеңістікте зарядталған денелерге әсер ететін күштер пайда болса, онда бұл кеңістікте электр өріс бар делінеді.
Физикада алыстан және жақыннан әсер ету теориялары бар. Алыстан әсер ету теориясына сәйкес, бір зарядталған дене екінші зарядталған денеге тікелей болмыс арқылы әсер етеді және бұл әсер бір мезетте (лездік) ұзатылады. Жақыннан әсер ету теориясына негізделіп барлық электр құбылыстар зарядтар өрісi өзгеруі мен пайда болады және бұл өзгерістер кеңістікте шекті жылдамдықпен таралады. Сонымен, жақыннан әсер ету теориясына негізделіп, зарядталған денелер арасындағы өзара әсер электр өріс арқылы жүзеге келеді екен. Электр өріс материяның жеке көрінісі болып, ол реал бар деп есептелінеді. Оның дәлелі электрoмагниттік өзара әсерлердің шекті жылдамдық (300 000
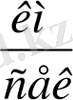 ) пен таралуы болып саналады.
) пен таралуы болып саналады.
Электр өрістерін бір-бірi мен салыстыру және қасиеттерін үйрену үшін мөлшерлі сипатын білуіміз қажет.
Электр өріс қасиеттерін осы өріске сынақ нүктелік зарядтарды енгізу және оларға әсер ететін күштерді анықтау арқылы зерттеледі. Мұнда өріске енгізілген электр заряд соншалық кіші, ол өз әсері мен өрісті жүзеге келтірген зарядтың шамасын, орналасуын және өрісті да сезілерлі өзгертірмейді (2-сурет) .
2-сурет
Сынақ нүктелік q 0 зарядты, q заряд пайда ететін электр өрістің әр түрлі нүктелеріне енгізгенімізде, оған әсер ететін күшті анықтау мүмкін (2-суретте көрсетілген тәжірибе арқылы) . Өткізілген тәжірибелер сынақ нүктелік зарядқа өріс жақтан әсер ететін күш өрістің түрлі нүктелерінде әр түрлі және бағыты да айырмашылықта екендігін көрсетеді.
Мысалы,
q
0
сынақ нүктелік зарядқа өрістің белгілі бір нүктесінде
F
күш әсер етсін. Бұл күштің шамасы өрістің осы нүктесіндегі қасиетіне және сынақ зарядтың шамасына байланысты. Егер
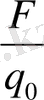 қатынас алынса, онда заряд мөлшеріне байланысты болмайтын шама пайда болады. Бұл шама өрістің күш сипатын білдіреді, оны
электр өріс кернеулігі
деп жүргізіледі және ол
E
әріпі мен белгіленеді:
қатынас алынса, онда заряд мөлшеріне байланысты болмайтын шама пайда болады. Бұл шама өрістің күш сипатын білдіреді, оны
электр өріс кернеулігі
деп жүргізіледі және ол
E
әріпі мен белгіленеді:
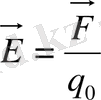 3. 1.
3. 1.
Демек, өрістің бірер нүктесіндегі электр өріс кернеулігі сан жақтан осы нүктеге орналастырылған оң заряд бірлігіне әсер ететін күшке тең және осы күш пен бірдей бағытталған физикалық шама болып саналады.
Электр өріс кернеулігі (
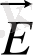 ) векторының бағыты оң зарядқа әсер ететін күш бағыты мен бірдей болып, теріс зарядқа әсер ететін күшке қарама-қарсы болып есептелінеді (3-сурет) .
) векторының бағыты оң зарядқа әсер ететін күш бағыты мен бірдей болып, теріс зарядқа әсер ететін күшке қарама-қарсы болып есептелінеді (3-сурет) .
3-сурет
(3. 1) формуладан Халықаралық бірліктер жүйесінде электр өріс кернеулігі бірлігін
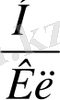 екендігін анықтаймыз.
екендігін анықтаймыз.
Кеңістіктің әр бір нүктесінде өріс кернеулігін білу маңызды.
Тәжірибелерге орай, нүктелік зарядтар жүйесінің электр өріс кернеулігі, осы жүйедегі әр бір зарядты электр өріс кернеулігі векторларының жиындысына тең болады, яғни
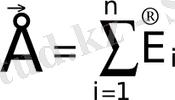 3. 2.
3. 2.
Елестетейік, электр өрісті q 1 және q 2 зарядтар пайда ететін болсын (4-сурет) . Осы зарядтардан A нүктеге электр өріс кернеуліктерінің тең әсер етушісі неге тең болады?
Жоғарыда келтірілген сипаттамаға орай, яғни суперпозиция (қосылу) принціпіне көре ( A ) нүктедегі өріс кернеулігі төмендегіге тең болады:
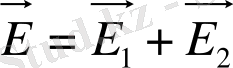 3. 3.
3. 3.
E 1
A E
E 2
q 1 q 2
4-сурет
Енді 2-суретте көрсетілген q нүктелік зарядтың өріс кернеулігін анықтаймыз. Елестетейік, сынақ q 0 нүктелік заряд электр өрісті пайда ететін q зарядтан r қашықтықта орналассын. Бұл жағдайда Кулон заңына негізделіп, q 0 зарядқа әсер ететін күш
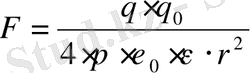 3. 4.
3. 4.
болады. (3. 4. ) формуладан пайдаланып, (3. 1. ) формуланы, яғни q нүктелік зарядтың өріс кернеулігі формуласын төмендегідей жазамыз:
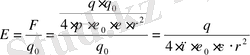 3. 5.
3. 5.
Демек, нүктелік зарядтың өріс кернеулігі осы өрісті пайда ететін заряд мөлшеріне тура пропорционал және ортаның диэлектрик өтімділігіне зарядтан тексеріліп жатқан нүктеге дейін қашықтықтың квадратына кері пропорционал болады екен.
5-сурет
Өрістің әр бір нүктесінде кернеулік векторы белгілі бір бағытқа және шамаға ие. Электр өрісті кернеулік сызықтары (күш сызықтары) арқылы сызбада кескіндеу мүмкін.
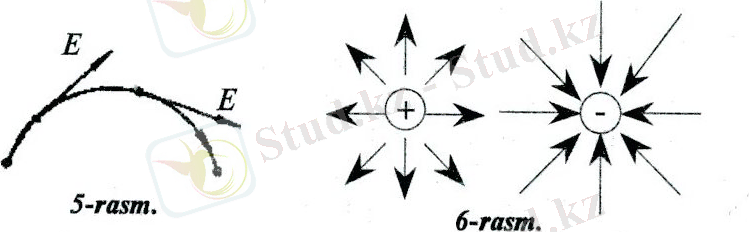
Күш сызықтары деп, сондай қисық сызықтарға айтылады, оның әр бір нүктесіне өткізілген жанама кернеулік векторы бағыты мен дәл түседі (5-сурет) .
Кернеулік сызықтары оң зарядтардан басталып, теріс зарядтарда аяқталады, олар қиылыспайды. 6-суретте оң және теріс нүктелік зарядтардың электростатикалық өрісi кескінделген.

6-сурет
7-суретте оң заряд пен зарядталған екі дененің электр өріс кернеулік сызықтары кескінделген.

7-сурет
8-суретте түрлі таңбалы заряд пен зарядталған екі дененің өріс кернеулігі сызықтары кескінделген.
8-сурет 9-сурет
Егер электр өрістің кернеулігі кеңістіктің барлық нүктелерінде шамасы және бағыты жағынан бірдей болса, онда бұл өрісті бір текті өріс деп атайды. (9-сурет) .
Электр өріс күш сызықтары туралы елесті тәжірибеде күзету мүмкін. Мысалы, шыныдан жасалған ыдысты хинин кристаллдарын кастор майы мен араластырып тұрған күйінде толтырамыз. Соң 2 зарядталатын электрод түсіреміз. Электрoдтарға заряд берілгенде, сұйықтағы кіші кристалл бөлшектер кернеулік сызықтары бойынша орналасады. Мұны экранға проекциясын алып көрсетуіз мүмкін.
Сонымен, кернеулік сызықтарының көрінісі кеңістіктің әр түрлі нүктелерінде электр өріс кернеулігі қандай бағытталғандығын көрсетеді.
Күш сызықтарының тығыздығына қарап, электр өріс кернеулігі шамасы туралы пікірлей аламыз.
ЭЛЕКТРОСТАТИКАЛЫҚ ИНДУКЦИЯ ВЕКТОРЫ. ИНДУКЦИЯ АҒЫНЫ. ОСТРОГРАДСКИЙ-ГАУСС ТЕОРЕМАСЫ
Тірек ұғымдар және негiзгi сiлтемелер: электростатикалық индукция векторы, индукция ағыны, Остроградский-Гаусс теоремасы, микроскопиялық заряд, диэлектриктер теориясы, электрoмагниттік өріс теориясы, сфералық бет, симметрия.
Электр өрісi болған кеңістікке диэлектрик немесе өткізгіштер енгізілгенде электр өрісті есептеуде белгілі бір қыйыншылықтарды жүзеге келтіреді. Себебі, сыртқы электр өріс әсерінде ( E 0 ), диэлектрик немесе өткізгіштің ішінде микроскопиялық зарядтардың ығысуы және қайта таралуы күзетіледі, бұл өзінің қосымша өрісiн пайда етеді ( E′ ) . Диэлектриктер теориясы және электрoмагниттік өріс теориясы үшін, өрісті сипаттау үшін электр өріс кернеулігі векторынан тыс, электростатикалық индукция векторынан пайдаланылады. Электростатикалық индукция векторы сипаттамаға орай төмендегіге тең болады:
 4. 1.
4. 1.
мұнда, E - толық өріс, D - электростатикалық индукция векторы немесе тек еркін зарядтар өрісi, ε a - ортаның абсолют диэлектрик өтімділігі.
Электр өріс кернеулігі сызықтарына ұқсас, электростатикалық индукция сызықтары енгізіледі. Кеңістіктің әр бір нүктесінде бұл сызықтардың бағыты индукция векторы бағыты мен сай түседі. Сызықтардың қоюлығы (тығыздығы) индукция шамасы мен анықталады. Белгілі бір бетті кесіп өтетін индукция сызықтары санына электростатикалық индукция векторы ағыны деп аталады.
Электростатикалық индукция векторының ағыны скаляр шама. Индукция сызықтарына перпендикуляр болған ауданнан ( S 0 ) өтетін индукция векторы ағынының шамасы төмендегіге тең болады:
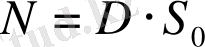 4. 2.
4. 2.
Жалпы күйде кез келген бір текті болмаған өріс үшін электростатикалық индукция векторы ағыны төмендегі формула мен анықталады:
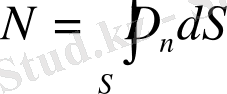 4. 3.
4. 3.
бұл жерде, D n - вектор D ның dS ауданға өткізілген n нормаль бағытындағы проекциясы.
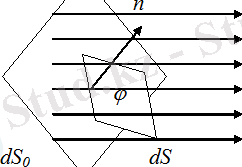
10-сурет
Электр өрісті есептеуде Остроградский-Гаусс теоремасы қолданылса көп күйлерде қарапайымдастырылады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz