ЭЛЕКТРОСТАТИКАЛЫҚ ӨРІСТЕ ЗАРЯДТЫ ОРЫН АУЫСТЫРУДА ОРЫНДАЛҒАН ЖҰМЫС

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

ЭЛЕКТРОСТАТИКАЛЫҚ ӨРІСТЕ ЗАРЯДТЫ ОРЫН АУЫСТЫРУДА ОРЫНДАЛҒАН ЖҰМЫС

Тірек ұғымдар және негiзгi сiлтемелер: электростатикалық өріс, заряд, орындалған жұмыс, өріс кернеулік циркуляциясы, потенциалдық өріс.

Елестетейік, электр өріс q оң заряд пайда ететін болсын (18-сурет).

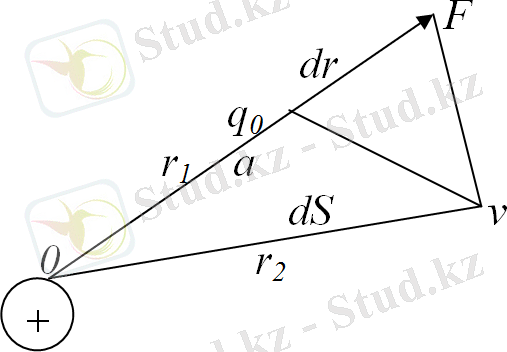
18-сурет

Осы өрістің a нүктесіне q0 нүктелік заряд енгізейік. Бұл q зарядқа күш әсерінде ол v нүктеге орын ауыстырады. F күштің dS қашықтықта орындаған жұмысы төмендегі формуламен өрнектеледі:
7.1.
- бұрыш, бұл күшпен dS орын ауыстыру бағыты арасындағы бұрыш.
7.2.
екендігін және күш орнына шаманы қойып, (7.1.) ді төмендегідей жазамыз,
7.3.
Сонымен, q0 зарядты a нүктеден v нүктеге орын ауыстыруда атқарылған жұмысты есептеу үшін, кернеулік

екендігін есепке алып, (7.3.) ді интегралдаймыз:
7.4.
бұл жерде, r1 және r2 - q зарядтан a және v нүктелеріне дейін болған қашықтық.
(7.4.) формуладан көрініп тұрғанындай, q заряд өрісінде зарядты орын ауыстыруда орындалған жұмыс заряд қозғалысының траекториясы пішініне байланысты емес. Ол тек q0 зарядтың бастапқы және соңғы күйлеріне, q0 және q зарядтардың шамасына және ортаның диэлектрик өтімділігіне байланысты екен.
Егер электр өріс нүктелік зарядтар жүйесі (q1, q2, ..., qn) жағынан жүзеге келіп жатқан болса, осы өрісте q0 нүктелік заряд енгізілсе, оған күштер әсер етеді. Осы күштердің тең әсер етушісі атқарған жұмыс әрбір күштің атқарған жұмыстарының алгебралық жиындысына тең болады:
7.5.
Оң зарядты, электр өріс күштері тұйық жол (контур) l бойынша орын ауыстыруда атқарылған жұмыс төмендегіге тең болады:
7.6.
бұл жерде, шама өріс кернеулігінің dr орын ауыстыру бағытына проекциясы, - шама өріс кернеулік циркуляциясы деп аталады.
(7.5.) формуладан көрініп тұрғанындай, тұйық жол бойынша электростатикалық өрісте зарядты орын ауыстыруда орындалған жұмыс нольге тең болады, себебі бастапқы және соңғы нүктелері сай түседі. Сол үшін
7.7.
бұл жерде,

болады, яғни электростатикалық өріс кернеулік векторы циркуляциясы нольге тең. Бұл күйде электростатикалық өріс потенциалдық өріс деп аталады.

ЭЛЕКТРОСТАТИКАЛЫҚ ӨРІС ПОТЕНЦИАЛЫ

Тірек ұғымдар және негiзгi сiлтемелер: электростатикалық өріс, потенциал, кернеу,СГСЭ, Вольт, потенциалдар айырмасы.

Алдын көріп шыққанымыздай, егер электростатикалық өрісте q0 зарядты орын ауыстыруда атқарылған жұмыс (8.4.) формула, тек зарядтарының шамасы және q0 зарядтың бастапқы және соңғы күйлеріне байланысты болса, бұл жұмыс осы зарядтың потенциалдық энергиясының кемеюіне тең болады:
8.1.
q0 зарядты шексіз өте ұсақ орын ауыстыруларында потенциалдық энергияның өзгеруі төмендегіге тең болады:
8.2.
Егер q0 зарядты 10-суретте көрсетілген күйлерде (a және v нүктелер) орын ауыстыруы болса, онда потенциалдық энергиясының өзгеруі
8.3.
болады.
Электр өрісінде q0 зарядтың потенциалдық энергиясы абсолют мәнін табу үшін өрісте сондай шартты нүктені алу керек болады, онда потенциалдық энергия нольге тең болады.
Сол үшін электр өрісін пайда етіп жатқан q зарядтан шексіздікде орналасқан нүктедегі q0 зарядтың потенциалдық энергиясы шартты нольге тең деп қабылданған ().
Онда q зарядтан r қашықтықта орналасқан q0 нүктелік зарядтың потенциалдық энергиясы төмендегі формула жәрдемінде анықталады:
8.4.
Сонымен, q0 заряд электр өрісінің белгілі бір нүктесінде (W) потенциалдық энергияға, өрістің әр түрлі нүктелерінде әр түрлі мәнге ие. Потенциалдық энергия өрістің қасиеттеріне және зарядтың шамасына байланысты. Егер қатынасты алсақ, онда бұл шама q0 заряд мөлшеріне байланысты болмайды, оны электростатикалық өрістің энергетикалық сипаты ретінде қабылданған. Бұл қатынас әріпімен белгіленіп, өріс потенциалы деп аталады:
8.5.
Демек, өріс потенциалы бұл сондай шама, зарядтың потенциалдық энергиясы электр өрістің белгілі бір нүктесіне орналастырылған заряд шамасы қатынасына тең.
Нүктелік q заряд потенциалын (8.4.) формуладан пайдаланып табамыз, яғни:
8.6.

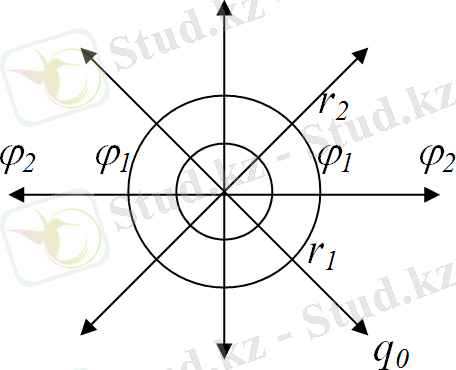
19-сурет

(8.4.) формуладан көрініп тұрғанындай, q заряд жүзеге келтірген электр өрісін r қашықтықтағы сфера бетіндегі барлық нүктелерде потенциал бірдей болады. Егер q зарядтан r2 қашықтықта өрістің барлық нүктелерінде (сфера бойынша) потенциал 2 бірдей болады (19-сурет).
Оң зарядтың электростатикалық өріс потенциалы, зарядтан қанша алыстаса сонша кемейеді, теріс зарядтың өріс потенциалы болса, керісінше, артып барады. Егер беттің барлық нүктелерінде потенциал бірдей болса, мұндай беттер эквипотенциалдық деп аталады ("ekvi" латынша сөз болып, тең деген мағынаны білдіреді).
Енді (8.5.) және (8.6.) формулалардан пайдаланып, электр өрісінде электр күштері q0 зарядты бір нүктеден екінші нүктеге орын ауыстыруда атқарылған жұмысты ((8.2.) және (8.3.) формулаларды) потенциалдар айырмасымен өрнектеуіміз мүмкін:
8.7.
Демек, электростатикалық өріс күштері нүктелік зарядты орын ауыстыруда атқарылған жұмыс осы орын ауыстырып жатқан зарядтың потенциалдар айырмасына (бастапқы және соңғы нүктелеріндегі потенциал) көбейтіндісіне тең. Потенциалдар айырмасын тәжірибеде өлшеу оңай және оны көбіне кернеу деп жүргізіледі, ол U әріпімен белгіленеді, яғни:
8.8.
Біз жоғарыда бір заряд пайда еткен өріс потенциалын үйрендік. Егер өрісті зарядтар жүйесі жүзеге келтіріп жатқан болса, онда күрделі өрістердің потенциалын анықтау үшін суперпозиция (сай келуі, қосылу) принципінен пайдаланылады. Потенциал скаляр шама болғандығы үшін суперпозиция (қосылу) принципіне негізделіп зарядтар жүйесін нәтижелік өріс потенциалы, осы өрісті құрайтын потенциалдардың алгебралық жиындысына тең болады. Мысалы, белгілі бір нүктеде қосылатын өрістердің потенциалдары 1, 2, ..., n болса, онда осы нүктеде нәтижелік өріс потенциалы төмендегіге тең болады:
8.9.
Потенциал және потенциалдар айырмасы бірлігі ретінде, ХБ жүйесінде қабылданған, яғни 1 Вольт потенциал бірлігі етіп өрістің сондай нүктесінің потенциалы қабылданған болып, онда 1 ге тең потенциалдық энергияға ие. Кернеу (потенциалдар айырмасы) бірлігі ретінде Вольт қабылданған, яғни электр өрісінің екі нүктесі арасында 1 Кулонға тең зарядты орын ауыстыруда орындалған жұмыс 1 Джоульға тең болса, осы өріс екі нүктесі арасындағы потенциалдар айырмасы 1 Вольтқа тең деп қабылданған. Вольт бірлігін төмендегідей жазуымыз мүмкін:
заряд бірлігі
немесе
потенциал бірлігі
U потенциалға ие болған өрістегі Q зарядтың потенциалдық энергиясы төмендегіге тең болады:

Электростатикалық өрісте зарядтың потенциалдық энергиясы салыстырмалы шама болып саналады.

ЭЛЕКТРОСТАТИКАНЫҢ ЖАЛПЫ МӘСЕЛЕСІ

Тірек ұғымдар және негiзгi сiлтемелер: потенциал, Лаплас теңдеуі, өткізгіш.

Зарядтар таралуы белгісіз, бірақ өткізгіштердің потенциалдары белгілі болған күйлер көп кездеседі. Мұндай мәселелерді төмендегідей тәрізде сипаттау мүмкін: пішіні және өзара орналасуы белгілі болған A, B, V және т.б. өткізгіштер жүйесі берілген және барлық өткізгіштердің потенциалдары UA, UB және т.б. лар белгілі, өткізгіштер арасындағы өрістің кез келген нүктесіндегі потенциал мәнін анықтау талап етіледі.
Бұл мәселе математикалық жақтан төмендегі күйге келтіріледі. Өріс кернеулігі E нің координаталары бойынша құраушыларын төмендегідей өрнектеу мүмкін:

Бұл өрнектерді Пуассон теңдеуіне қойып, жалпы теңдеуді пайда етеміз, оны төмендегі көріністегі потенциал қанағаттандырады:
9.1.
Егер өткізгіштер арасында зарядтар болмаса, онда барлық нүктелерде =0 болады және (9.1.) теңдеу қарапайым көрініске келеді:
9.2.
Бұл теңдеу Лаплас теңдеуі деп аталады. Сол үшін потенциалды жалпы есепте есептеу координаталарының осындай функциясы U (x, y, z) ті табуға келтіріледі, бұл функция өткізгіштер арасындағы толық кеңістікте (9.2.) дифференциал теңдеуді қанағаттандырады, өткізгіштердің өзінде болса UA, UB және т.б. берілген тұрақты мәндерді алады. Мұндай мәселенің шешімі бір мәнді болады.
ЭЛЕКТР ӨРІСІНДЕ ӨТКІЗГІШТЕР ЖӘНЕ ДИЭЛЕКТРИКТЕР

Тірек ұғымдар және негiзгi сiлтемелер: электр өрісі, өткізгіштер, диэлектриктер, полюсталған диэлектрик, электростатикалық индукция.

Өткізілген тәжірибелер көрсетіп тұрғанындай, денелердің түзілісі және қасиеттеріне байланысты болған күйде оларға берілген q заряд дене бойынша таралады немесе белгілі бір берілген жерде қалады. Егер денелерге берілген q заряд толық дене бойынша еркін орын ауыстырса, мұндай ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.