Квадрат теңдеуді шешудің әдістері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ КІШІ ҒЫЛЫМ АКАДЕМИЯСЫ

МАЛАЯ АКАДЕМИЯ НАУК РЕСПУБЛИКИ КАЗАХСТАН

Тақырыбы: Квадрат теңдеулерді шешудің әр түрлі әдістері

Секция: Математика

Аты-жөні: Әкімбай Дәурен Жанатұлы

Сыныбы: 9

Оқу орны: Оян ауылындағы МДШО бар орта мектебі

Жетекшісі: Анешова Таңшолпан Болысбекқызы

«Разные способы решения квадратных уравнений»

Средная школа с ДМЦ с

Үштөбе қаласы, 2018 жыл

«КВАДРАТ ТЕҢДЕУЛЕРДІ ШЕШУДІҢ ӘР ТҮРЛІ ӘДІСТЕРІ»

Әкімбай Дәурен, 9-сынып, Оян ауылындағы МДШО бар орта мектебі,

Қаратала ауданы, Оян ауылы

Болжау: Квадрат теңдеулерді пайдалана білетін оқушы болашақта өзінің білімін әр-түрлі салаларда пайдалана алады, еліміздің дамуына зор үлесін қосады.

Өзектілігі: Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты білімді маман қалыптасады.

Зерттеу жұмысының мақсаты: Квадрат теңдеулерді шешудің жолдарын, әдіс-тәсілдерін қарастыру. Осы тәсілдерді теңдеуді шешуде қолдануды көрсету.

Зерттеу кезеңдері :

тақырыпты негіздеу, мақсаттары мен міндеттерін айқындау;
тақырыпқа байланысты материалдар жинақтау, талдау, әдебиеттерге шолу жасау;
квадрат теңдеулердің түрлерін қарастыру;
алынған нәтижелер бойынша есептер жинағын құру, жинақтау;
жұмысты қорытындылау.

Зерттеудің жаңашылдығы : Квадрат теңдеулердің оқулықта қарастырылмаған шешу жолдарын қарастыру.

Мазмұны.

I. КІРІСПЕ БӨЛІМ … . . . … . . . 3

1. 1 Квадрат теңдеудің даму тарихы . . . … . . . . . … . . . 3

1. 2 Квадрат теңдеудің әл-Харезмде дамуы . . . …… . . . … . . . 4 II. НЕГІЗГІ БӨЛІМ

2. 1. Квадрат теңдеудің анықтамасы . . . 6

2. 2. Толымсыз квадрат теңдеулер . . . 6

2. 3. Квадрат теңдеуді шешудің әдістері . . . 6

2. 4. Квадрат теңдеулерді пайдаланып есептер шығару . . . 10

ІІІ. ҚОРЫТЫНДЫ . . . 15

IV. ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 16

Кіріспе

Көптеген табиғи процестер мен құбылыстар квадрат теңдеулер арқылы сипатталады, мазмұнды есептердің көбісінің шешуі квадрат теңдеулерді шешуге келіп тіреледі. Квадрат теңдеулерді шешу математикада қарастырылатын тақырыптардың қажетті бірі болып табылады. Зерттеу барысында мектеп оқушыларына «квадрат теңдеулерді» шешу жолдарынының алты түрлі әдісімен таныстыруға мүмкіндік бар екендігін анықтадым. Ол тәсілдерге алда жеке-жеке тоқталамын.

1. 1 Квадрат теңдеудің даму тарихы.

2-ші дәрежелі теңдеулерді шешуді б. э. д II мыңжылдықта Ежелгі Вавилонда шығара білген. Ежелгі Греция математиктері квадрат теңдеулерді геометриялық тәсілмен шешкен; мысалы, Евклид -кесіндіні орта және шеткі қатынастарға бөлу арқылы шешкен. Квадрат теңдеудің түбірлерінің формуласы бірнеше рет «қайтадан ашылған» . Бізге жеткен деректер бойынша ең бірінші бұл формулаларды үнді математигі Брахмагупте ашқан(жуықтап 598 ж. ) . Ортаазия ғалымы ал-Хорезми (IX . ғ) өзінің «Китаб аль-джебр валь -мукабала» трактатында бұл формуланы екімүшенің толық квадратын геометриялық интерпретация арқылы айырып алу жолымен шешкен.

1. 2 Квадрат теңдеудің әл-Харезмде дамуы.

Кітаптың өзінде пайдаланылған әдебиеттер көрсетілмегендіктен, әл-Хорезми қандай кітаптарды қолданылғаны белгісіз.

Кітапта кез келген квадрат теңдеуді алты негізгі түрдің біріне келтіріп, сол негізгі түрлерді шешудің алгебралық және геометриялық тәсілдері келтірілген. Қазіргі кезде қолданылатын абстрактылы шартты белгілер кітапта атымен жоқ болғандықтан, «әл-Хорезмидің алгебрасы толығымен сөзбен сипаттау арқылы баяндалған. Гректің «Арифметикасында» немесе Браһмагуптаның еңбектерінде қолданылатын синкопациялар мүлдем қолданылмаған. Тіпті сандар арнайы таңбамен бейнеленген емес, толығымен сөздер ретінде жазылған!»Сондықтан теңдеулер сөзбен «шаршы» деп (яғни бүгіндері “x ² ” деп), «түбір» деп (бүгін оны “x” деп) және «сандар» деп (мысалы, «қырық екі», «жеті» деп толығымен жазып отырды) деп белгіленіп отырды. Бүгінгі күннің шартты белгілерін қолданса, теңдеудің негізгі алты түрі мыналар:
1) квадраттар тең түбірге тең (ax ² = bx)
2) квадраттар санға тең (ax ² = c)
3) түбірлер санға тең (bx = c)
4) квадраттар мен түбірлер санға тең (ax ² + bx = c)
5) квадраттар мен сандар түбірге тең (ax ² + c = bx)
6) түбірлер мен сандар квадраттарға тең (bx + c = ax ² )

Әл-жәбр (араб жазуымен: ‘الجبر’) («толықтыру») амалы: теріс шаманы теңдеудің бір жағынан екінші жағына жіберіп, оң шама етіп өзгерту.
Әл-Хорезмидің мысалында (қазіргі белгілерді қолданса) “x ² = 40x - 4x ² ” теңдеуі «әл-жәбр» амалын қолдану арқылы мынаған өзгертіледі: “5x ² = 40x” Осы ережені қайталап қолдану арқылы есептеулерді пайда болатын теріс сандардан құтылуға болады.

Әл-мұқабала (араб жазуымен ‘المقابله’) («теңдестіру») дегеніміз - теңдеудің екі жағынан да бірдей оң шаманы алып тастау, сонда мына теңдеу: “x2 + 5 = 40x + 4x ² ” мына түрге келеді: “5 = 40x + 3x ² “. Осы ережені қайталап қолдану арқылы әр түрлі шамалардың (квадрат, түбір, сан сияқты) теңдеудің бір жағында тек бір рет қана кездесетіндей етіп түрлендіруге болады.
Кітаптың келесі бөлігінде жоғарыда айтылған ережелерді іс жүзінде қолданудың практикалық мысалдары келтірілген. Одан кейінгі бөлігінде аудан мен көлемді есептеудің жолдары қарастырылған.

2. 1 Квадрат теңдеудің анықтамасы.

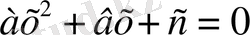(1) түрінде берілген теңдеу квадрат теңдеу деп аталады.

Мұндағы а, в, с нақты сандар. ,

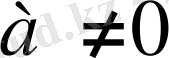а - бірінші коэффициент, в - екінші коэффициент, с- бос мүше.

Егер (1) теңдеудегі болса, онда ол теңдеу толық квадрат теңдеу деп аталады. Іс жүзінде кездесетін көптеген есептерді шешу, мысалы 2 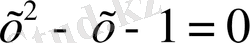, 3 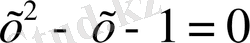түрдегі мысалдарды алуға болады.

2. 2 Толымсыз квадрат теңдеулер

Егер ах ² +вх+с=0 түріндегі теңдеудің в немесе с, немесе в мен с нөлге тең болатын дербес жағдайлардағы квадрат теңдеу толымсыз квадрат теңдеу деп аталады. Толымсыз квадрат теңдеулер былай жазылады.

1. 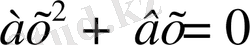, мұндағы с=0.

2. 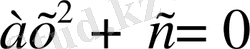, мұндағы в=0.

3. 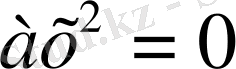, мұндағы в=0, с=0. Мысалы: 2 х ² = 0 , в =с=0, х ² + х - 7 = 0, в =0 және

х ² + 6х = 0, с =0

2. 3 Квадрат теңдеуді шешудің әдістері

1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу.

х ² + 10х - 24 = 0 теңдеуді жіктейміз .

Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:

х ² + 10х - 24 = х ² + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12) (х - 2) .

Демек, теңдеуді былай жазуға болады:

(х + 12) (х - 2) = 0

Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х = 2 және х = - 12 сандары х ² + 10х - 24 = 0 теңдеуінің түбірлері болып табылады.

2-әдіс. Толық квадратқа келтіру әдісі.

Мысал: х ² + 6х - 7 = 0 теңдеуін шешейік.

Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х ² + 6х өрнегін төмендегідей жазып аламыз:

х ² + 6х = х ² + 2• х • 3.

Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 3-тің екі еселенгені. Толық квадрат алу үшін 3 ² -ын қосу керек. Сонда

х ² + 2• х • 3 + 3 ² = (х + 3) ² .

Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 3 ² -ын қосып, алып тастаймыз. Сонда шығатыны:

х ² + 6х - 7 = х ² + 2• х • 3 + 3 ² - 3 ² - 7 = (х + 3) ² - 9 - 7 = (х + 3) ² - 16.

Сонымен, берілген теңдеуді былайша жазуға болады:

(х + 3) ² - 16 =0, (х + 3) ² = 16.

Бұдан, х + 3 - 4 = 0, х ₁ = 1, немесе х + 3 = -4, х ₂ = -7.

3-әдіс. Квадраттық теңдеулерді формула арқылы шешу.

ах ² + bх + с = 0, а ≠ 0

теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:

4а ² х ² + 4аbх + 4ас = 0,

((2ах) ² + 2ах • b + b ² ) - b ² + 4ac = 0,

(2ax + b) ² = b ² - 4ac,

2ax + b = ± √ b ² - 4ac,

2ax = - b ± √ b ² - 4ac,

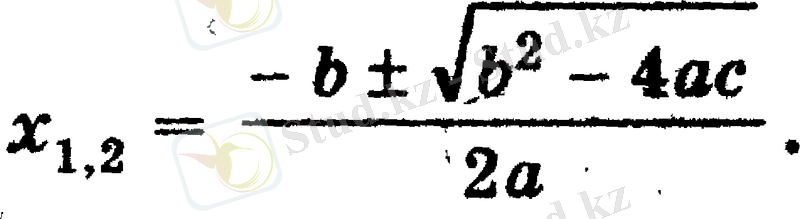
Оған келесідегідей мысалдар келтіруге болады: 4х ² + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b ² - 4ac = 7 ² - 4 • 4 • 3 = 49 - 48 = 1,

Д>0 болғандықтан, екі әр түрлі түбір болады:

Сонымен, дискриминант оң болғанда, яғни в ² -4ас>0, ах ² +вх+с=0 теңдеуінің екі түрлі түбірі болады.

б) 4х ² - 4х + 1 = 0, теңдеуін шешейік.

а = 4, b = - 4, с = 1, D = b ² - 4ac = (-4) ² - 4 • 4 • 1= 16 - 16 = 0,

D = 0, болғандықтан, бір ғана түбір бар болады

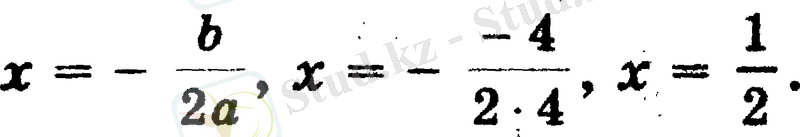
Сонымен, егер дискриминант нөлге тең болса, b ² - 4ac = 0 , сонда

ах ² + bх + с = 0 теңдеуінің жалғыз түбірі бар болады

в) 2х ² + 3х + 4 = 0, теңдеуін шешейік.

а = 2, b = 3, с = 4, D = b ² - 4ac = 3 ² - 4 • 2 • 4 = 9 - 32 = - 13, D < 0.

Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды. .

Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды. b ² - 4ac < 0 онда ах ² + bх + с = 0 теңдеуінің түбірі болмайды

4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу

Келтірілген түбірлері Виет теоремасын қанағаттандырады. Ол былай беріледі: х ² + px + c = 0. (1) а=1 болғанда, x ₁ x ₂ = q, x ₁ + x ₂ = - p

Бұдан келесі тұжырымдарды шығаруға болады: а) Егер q (1) теңдеудің бос мүшесі оң болса (q0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.

Мысал, x ² - 3x + 2 = 0; x ₁ = 2 және x ₂ = 1, мұнда q = 2 > 0 , p = - 3 < 0;

x ² + 8x + 7 = 0; x ₁ = - 7 және x ₂ = - 1, мұнда q = 7 > 0 , p= 8 > 0.

б) Егер q (1) теңдеудің бос мүшесі теріс болса (q <0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р <0 болса, теріс болады, егер р >0.

Мысал:

x ² + 4x - 5 = 0; x ₁ = - 5 , x ₂ = 1, м ұнда q= - 5 < 0 , p = 4 > 0;

x ² - 8x - 9 = 0; x ₁ = 9 и x ₂ = - 1, мұнда q = - 9 < 0, p = - 8 < 0.

5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу

ах ² + bх + с = 0, а ≠ 0 . квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз:

а ² х ² + аbх + ас = 0. . ах = у деп белгілесек, х = у/а

Олай болса у ² + by + ас = 0, еңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у ₁ , у ₂ -ні Виет теоремасы арқылы табамыз.

Соңында х ₁ = у ₁ /а , х ₁ = у ₂ /а -ны аламыз. Бұл жағдайда а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті «асыра лақтыру» әдісі деп атайды . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.

мысалы, 2х ² - 11х + 15 = 0 теңдеуін шешейік.

Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде: у ² - 11у + 30 = 0. Виет теоремасы бойынша

у ₁ = 5 х ₁ = 5/2 x ₁ = 2, 5

у ₂ = 6 x ₂ = 6/2 x ₂ = 3.

Жауабы: 2, 5; 3.

6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану.

ах ² + bх + с = 0, , а ≠ 0 квадрат теңдеуі берілген.

1) Егер, а+ b + с = 0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда

х ₁ = 1, х ₂ = с/а.

Дәлелдеу: а ≠ 0, келесідей квадрат теңдеуге келеміз.

x ² + b/a • x + c/a = 0.

Виет теоремасы арқылы

x ₁ + x ₂ = - b/a,

x ₁ x ₂ = 1• c/a.

а - b + с = 0 шарты бойынша, b = а + с аламыз. Олай болса,

x ₁ + x ₂ = - а + b/a= -1 - c/a,

x ₁ x ₂ = - 1• ( - c/a),

х ₁ = -1 , х ₂ = c/a болатынын дәлелдндік.

Мысал:345х2- 137х - 208 = 0теңдеуін шешейік.

Шешуі. а + b + с = 0 (345 - 137 - 208 = 0),

онда

х ₁ = 1, х ₂ = c/a = -208/345.

Жауабы: 1; -208/345.

2) 132х ² - 247х + 115 = 0 теңдеуін шешейік.

Шешуі. а + b + с = 0 (132 - 247 + 115 = 0),

онда

х ₁ = 1, х ₂ = c/a = 115/132.

Жауабы: 1; 115/132.

2. 4. Квадрат теңдеулерді пайдаланып есептер шығару

№1 есеп . Мәжіліске қатысушылар бір-бірімен сәлемдесіп қол алысқан, біреу қол алысудың барлық саны 66 болғанын санапты. Мәжіліске қанша адам келген?

Шешуі :

Мәжіліске қатысушы-х адам

Әр қайсысы х-1 адаммен қол алысқан.

Барлық қол алысу х(х-1)

$\frac{х(х - 1) }{2} = 66$ $\frac{х(х - 1) }{2} = 66$ х ² -х-132=0

$x = \frac{1 \pm \sqrt{1 + 528}}{2}$ $x = \frac{1 \pm \sqrt{1 + 528}}{2}$

х ₁ =12 х ₂ =-11

Жауабы: х=12

№2 есеп. Бір ұядағы барлық бал арасының жартысының квадрат түбіріне тең аралар жасмин бұтасына қонған, олардың артында аралардың $\frac{8}{9}$ $\frac{8}{9}$ -і қалған. Лотостың хош иісті гүлінің тұзағына абайсызда түсіп калған серік арасының ызыңына ұшып келген осы ұядағы аралардың тек біреуі ғана лотосты айналып ұшып жүр. Бір ұяда қанша бал арасы болған?