Алгебралық операциялар және олардың қасиеттері: топтар, сақиналар және өрістер


№ 3 дәрістің тақырыбы. Алгебралық операциялар, олардың қасиеттері. Топтар, мысалдары. Сақиналар, мысалдары.
Мақсаты:
1. Алгебралық операциялар түсінігін енгізу. Олардың қасиеттерін қарастыру.
2. Топтар теориясының негізгі түсініктерін енгізу.
3. Сақиналар, өріс теориясының негізгі түсініктерін енгізу.
Жоспар.
1. Алгебралық операциялар және олардың қасиеттері. Алгебралық жүйелер.
2. Топтар, мысалдары. Топтардың қарапайым қасиеттері. Ішкі топтар. Топтардың гомоморфтылығы және изоморфтылығы.
3. Сақина, сақинаның мысалдары. Қарапайым қасиеттері. Ішкі сақиналар. Бүтін сандар сақинасы. Сақиналардың гомоморфтылығы және изоморфтылығы. Өріс. Рационал сандар өрісі.
Қолданылатын көрнекі құрал және техникалық құралдар: презентациялар, кестелер.
Дәріс түрі: оқу дәрісі
1. Алгебралық операциялар және олардың қасиеттері. Алгебралық жүйелер.
Анықтама.
Бос емес
 жиынында анықталған бинарлық алгебралық операция деп,
жиынында анықталған бинарлық алгебралық операция деп,
 жиынына тиісті анықталған ретте алынған кез келген
жиынына тиісті анықталған ретте алынған кез келген
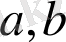 элементтеріне осы жиыннан үшінші жалғыз элементті сәйкестендіретін ереже немесе заң аталады.
элементтеріне осы жиыннан үшінші жалғыз элементті сәйкестендіретін ереже немесе заң аталады.
Анықтама.
Бос емес
 жиынындағы бинарлық алгебралық операция деп
жиынындағы бинарлық алгебралық операция деп
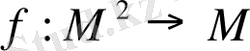 бейнелеуі аталады. (
бейнелеуі аталады. (
 кез келген реттелген қосқа
кез келген реттелген қосқа
 анықталған элемент сәйкестендіріледі)
анықталған элемент сәйкестендіріледі)
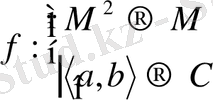
 элементі
элементі
 және
және
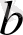 элементтеріне қолданған операцияның қорытындысы деп аталады.
элементтеріне қолданған операцияның қорытындысы деп аталады.
Мысалы:
1.
 натурал сандар жиынында «-» амалы алгебралық операция емес.
натурал сандар жиынында «-» амалы алгебралық операция емес.
2.
 бүтін сандар жиыны қосу және көбейту амалдары - алгебралық операциялар.
бүтін сандар жиыны қосу және көбейту амалдары - алгебралық операциялар.
3.
 - барлық ішікі жиындардың жиынындағы бірігу және қиылысу амалдары алгбралық операциялар.
- барлық ішікі жиындардың жиынындағы бірігу және қиылысу амалдары алгбралық операциялар.
4. Барлық бүтін тақ сандар жиыны көбейту амалына қатысты тұйықталған, ал қосу амалына қатысты тұйықталмаған.
5. Барлық бүтін жұп сандар жиыны қосу және көбейту амалдарына қатысты тұйықталған.
алгебралық операциядағы
қосының бейнесін, мұндағы
,
деп белгілейміз. (Бинарлық қатынастарды белгілеу үшін басқа да арнайы символдар қолданылады, мысалы
,
, +) .
Бинарлық операциялармен қатар жалпы n - арлық операциялар да қарастырылады (при n =1 болса, унарлық, n=3 болса, тернарлық және т. б. ), .
Биналық алгебралық операциялардың қасиеттері
 ,
,
 -
-
 жиынындағы кез келген алгебралық операциялар болсын.
жиынындағы кез келген алгебралық операциялар болсын.
1.
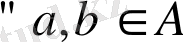 үшін а
үшін а
 b=b
b=b
 a орындалса, онда
a орындалса, онда
 алгебралық операциякоммутативті деп аталады.
алгебралық операциякоммутативті деп аталады.
2.
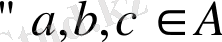 үшін a
үшін a
 (b
(b
 c) =(а
c) =(а
 b)
b)
 cорындалса, онда
cорындалса, онда
 алгебралық операция ассоциативті деп аталады.
алгебралық операция ассоциативті деп аталады.
3.
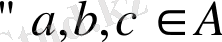 үшін a
үшін a
 (b
(b
 c) =(a
c) =(a
 b)
b)
 (a
(a
 c) орындалса, онда
c) орындалса, онда
 алгебралық операция
алгебралық операция
 алгебралық операцияға қатысты дистрибутивті деп аталады.
алгебралық операцияға қатысты дистрибутивті деп аталады.
Анықтама: Егер кез келген
 үшін келесі теңдік орындалса,
үшін келесі теңдік орындалса,
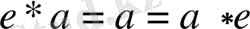 , онда
, онда
 элементі
элементі
 операцияға қатысты бейтарап элемент деп аталады.
операцияға қатысты бейтарап элемент деп аталады.
Мысалы:
1. 0 саны - «+» амалы үшін бейтарап элемент
2. 1 саны - «
 » амалы үшін бейтарап элемент.
» амалы үшін бейтарап элемент.
Анықтама: Егер
 теңдігі орындалса, онда
теңдігі орындалса, онда
 операциясына қатысты
операциясына қатысты
 элементі
элементі
 элементіне симметриялы деп аталады.
элементіне симметриялы деп аталады.
Мысалы:
1. «+» амалына
 элементіне
элементіне
 элементі қарама-қарсы, яғни кері элемент. 2. «
элементі қарама-қарсы, яғни кері элемент. 2. «
 » амалына
» амалына
 элементіне
элементіне
 элементі кері элемент болады.
элементі кері элемент болады.
Алгебралық операцияларды жазудың және терминологиясының екі түрі бар.


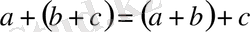
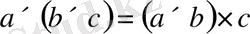
3.
 ,
,

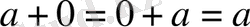 бейтарап элементтің табылуы
бейтарап элементтің табылуы
3.
 ,
,

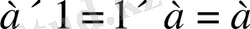 бейтарап элементтің табылуы
бейтарап элементтің табылуы
4.
 үшін
үшін
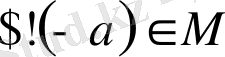
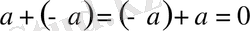 симметриялы элементтің бар болуы
симметриялы элементтің бар болуы
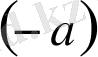 қарама - қарсы элемент деп аталады
қарама - қарсы элемент деп аталады
4.
 үшін
үшін
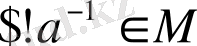
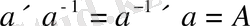 симметриялы элементтің бар болуы
симметриялы элементтің бар болуы
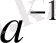 - кері элемент деп аталады
- кері элемент деп аталады
5.

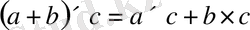
«сол жақтан»
«оң жақтан»
Мысалдар:
1. Рационал сандарда косу және көбейту амалдары - коммутативті, ассоциативті бинарлық операциялар болады.
2. Азайту операциясы рационал сандар жиынында коммутативті емес, ассоциативті емес.
3. М жиынының ішкі жиындарының қиылысуы және бірігуі коммутативті, ассоциативті
Анықтама.

 жиынындағы алгебралық операция болсын.
жиынындағы алгебралық операция болсын.
 .
.
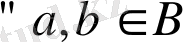 үшін
үшін
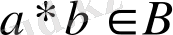 болса, онда
болса, онда
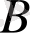 ішкі жиын
ішкі жиын
 жиынында
жиынында
 операцияға қатысты тұйықталған деп аталады.
операцияға қатысты тұйықталған деп аталады.
Мысалы:
1. Барлық бүтін жұп сандар жиыны «+», «
 » амалдарына қатысты
» амалдарына қатысты
 бүтін сандар жиынында тұйықталған
бүтін сандар жиынында тұйықталған
2. Барлық тақ сандар жиыны «
 » амалына қатысты тұйықталған, ал «+» амалына қатысты тұйықталмаған.
» амалына қатысты тұйықталған, ал «+» амалына қатысты тұйықталмаған.
Алгебра курсында анықталған операциялары бар жиындар оқытылады.
А- бос емес жиын болсын, ал
 - А жиынында берілген операциялар жиыны.
- А жиынында берілген операциялар жиыны.
Анықтама. Алгебра
деп
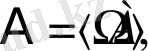 реттелген қос аталады, яғни алгебра- алгебралық операциялары бар бос емес жиын.
А
жиыны ақырлы немесе шексіз болуы мүмкін, ал
реттелген қос аталады, яғни алгебра- алгебралық операциялары бар бос емес жиын.
А
жиыны ақырлы немесе шексіз болуы мүмкін, ал
 - ақырлы жиын.
- ақырлы жиын.
А
жиыны
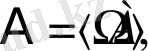 алгебрасының негізгі жиыны, ал оның элементтері -
алгебрасының негізгі жиыны, ал оның элементтері -
 алгебрасының элементтері деп аталады.
А
жиынында анықталған
алгебрасының элементтері деп аталады.
А
жиынында анықталған
 операциялар жиыны -
операциялар жиыны -
 алгебрасының бас операциялары деп аталады.
алгебрасының бас операциялары деп аталады.
Анықтама.
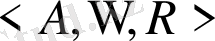 - реттелген үштік
алгебралық жүйе
деп аталады, мұндағы
А
- бос емес негізгі жиын;
- реттелген үштік
алгебралық жүйе
деп аталады, мұндағы
А
- бос емес негізгі жиын;
 -
А
жиынындағы алгебралық операциялар жиыны; R- алгебралық жүйедегі қатынастар жиыныр.
-
А
жиынындағы алгебралық операциялар жиыны; R- алгебралық жүйедегі қатынастар жиыныр.
 негізгі операциялар, R- негізгі қатынастар деп аталады.
негізгі операциялар, R- негізгі қатынастар деп аталады.
2. Топтар, мысалдары. Топтардың қарапайым қасиеттері. Ішкі топтар. Топтардың гомоморфтылығы және изоморфтылығы.
Топтар - алгебралық жүйелердің негізгі типтерінің бірі, ал топтар теориясы - қазіргі заманғы алгебраның негізгі бөлмдерінің бірі. Топтар теориясы үшін көптеген математикалық зерттеулер арналған. Олар математиканың әртүрлі бөлімдерінде қолданылады. Топтар теориясының негізін салушы
француз математигі Эварист Галуа (1811-1832) . «Топ» терминін енгізген де осы ғалым болатын.
Топтар теориясының міндеті - топтық операцияларды зерттеу.
Анықтама.
Егер бос емес А жиынында
 бинарлық операция ассоциативті болса, онда <A,
бинарлық операция ассоциативті болса, онда <A,
 > алгебрасы жартылай топ деп аталады яғни кез келген a, b, c
> алгебрасы жартылай топ деп аталады яғни кез келген a, b, c
 A элементтері үшін (a
A элементтері үшін (a
 b)
b)
 c=a
c=a
 (b
(b
 c) орындалады.
c) орындалады.
Анықтама.
Бірі бар <A,
 > жартылай топ
моноид
деп аталады, яғни a
> жартылай топ
моноид
деп аталады, яғни a
 A кез келген элемент үшін, a
A кез келген элемент үшін, a
 e=e
e=e
 a=a орындалатындай, e
a=a орындалатындай, e
 A бірлік элемент табылады.
A бірлік элемент табылады.
Анықтама.
Моноид деп
 бинарлық операция келесі шарттарды қанағаттандыратын:
бинарлық операция келесі шарттарды қанағаттандыратын:
1)
 бинарлық операция ассоциативті
бинарлық операция ассоциативті
2) e -
 бинарлық операцияға қатысты бейтарап элемент болатын
бинарлық операцияға қатысты бейтарап элемент болатын
 алгебрасы аталады.
алгебрасы аталады.
Мысалы:
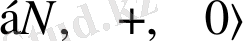 - натурал сандардың аддитивті моноиды;
- натурал сандардың аддитивті моноиды;
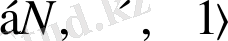 - натурал сандардың мультипликативті моноиды.
- натурал сандардың мультипликативті моноиды.
Анықтама.
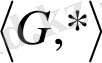 алгебрасы топ деп аталады, егер төмендегідей шарттарды қанағаттандырса:
алгебрасы топ деп аталады, егер төмендегідей шарттарды қанағаттандырса:
1)
 алгебрасы жартылай топ болса;
алгебрасы жартылай топ болса;
2) қайтымды операциясы анықталған болса.
Анықтама.
 бір бинарлық операциясы бар G жиыны топ деп аталады, егер келесі шарттар орындалса:
бір бинарлық операциясы бар G жиыны топ деп аталады, егер келесі шарттар орындалса:
1. операция ассоциативті, яғни кез келген a, b, c
 G үшін (a
G үшін (a
 b)
b)
 c=a
c=a
 (b
(b
 c) орындалады;
c) орындалады;
2. Бірлік элементтің табылуы, яғни G жиынында e - бірлік элемент табылады, кез келген a
 G үшін a
G үшін a
 e=e
e=e
 a=a орындалады;
a=a орындалады;
3. Кері элементтің табылуы, яғни кез келген a
 G үшін a
G үшін a
 x=x
x=x
 a=e орындалатындай, а - ға кері деп аталатын, G жиынында x элементі табылады.
a=e орындалатындай, а - ға кері деп аталатын, G жиынында x элементі табылады.
Анықтама.
Егер топтағы элементтер саны шектеулі болса, топ
шектеулі
деп аталады, топтағы элементтер саны
топтың реті
деп аталады.
Ал, топтағы элементтер саны шектеусіз болса, шектеусіз топ деп аталады.
Анықтама. Егер топтағы элементтер саны шектеулі болса, топ шектеулі деп аталады, топтағы элементтер саны топтың реті деп аталады.
Ал, элементтер саны шектеусіз топ, шектеусіз топ деп аталады.
Анықтама.
Егер
 - операциясы «қосу» болса, онда топ
аддитивті,
ал егер
- операциясы «қосу» болса, онда топ
аддитивті,
ал егер
 - операциясы «көбейту» болса, онда топ
мультипликативті
деп аталады
.
- операциясы «көбейту» болса, онда топ
мультипликативті
деп аталады
.
Анықтама.
Егер
 тобында
тобында
 бинарлық операция коммутативті болса, онда топ коммутативті топ немесе абельді топ деп аталады.
бинарлық операция коммутативті болса, онда топ коммутативті топ немесе абельді топ деп аталады.
Мысалдар:
1.
 - натурал сандар жиыны мультипликативті моноид.
- натурал сандар жиыны мультипликативті моноид.
1.
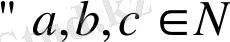 үшін
үшін
 ассоциативтілік орындалады.
ассоциативтілік орындалады.
2.
 ,
,
 үшін
үшін
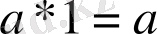 бейтарап элемент табылады.
бейтарап элемент табылады.
3.
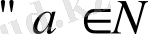
 - натурал сандар жиынының мультипликативті моноиды.
- натурал сандар жиынының мультипликативті моноиды.
2.
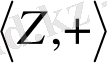 - бүтін сандар жиыны аддитивті, абельді топ.
- бүтін сандар жиыны аддитивті, абельді топ.
1.
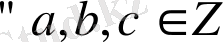 үшін
үшін
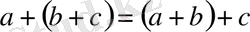 ассоциативтілік орындалады.
ассоциативтілік орындалады.
2.
 ,
,
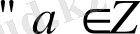 үшін
үшін
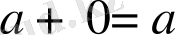 бейтарап элемент табылады.
бейтарап элемент табылады.
3.
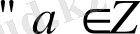 үшін
үшін
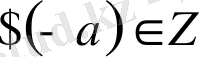
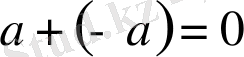 - кері элемент табылады.
- кері элемент табылады.
4.
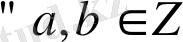 үшін
үшін
 орындалады.
орындалады.
G жиыны қандай да бинарлық операцияға қатысты топ болсын. H жиыны G жиынының ішкі жиыны болсын.

Анықтама. Егер G жиынының H ішкі жиыны сол бинарлық операцияға қатысты топ болса, онда ол G тобының ішкі тобы деп аталады.
Мысалы:
1) Z бүтін сандар жиынының қосу амалына қатысты тобы R нақты сандар жиынының қосу амалына қатысты тобының ішкі тобы;
2) Q рационал сандар жиынының қосу амалына қатысты тобы R нақты сандар жиынының қосу амалына қатысты тобының ішкі тобы;
Теорема. G тобының Н ішкі жиыны ішкі топ болу үшін келесі шарттардың орындалуы қажет:
1) G тобындағы амалдың Н жиынында анықталуы.
2)
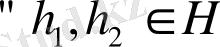
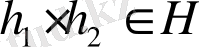 - тұйықталу шарты.
- тұйықталу шарты.
3)
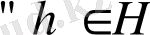

Теорема. Топтың кез келген ішкі тобы топ болып табылады. Топтың бейтарап элементі оның кез келген ішкі тобының бейтарап элементі болып табылады. Топтың гомоморфизмі және изоморфизмі. Изоморфизмның қасиеттері
Егер М жиынының әрбір элементіне, М жиынының қандай-да бір элементі сәйкестендірілсе, онда М жиынын өзіне-өзін бейнелеу берілді дейміз.
Егер
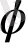 - М жиынын өзіні-өзін бейнелеу болса, ал а - М жиынының элементі болса, онда
- М жиынын өзіні-өзін бейнелеу болса, ал а - М жиынының элементі болса, онда
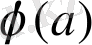 М жиынындағы а элементінің бейнесі деп аталады.
М жиынындағы а элементінің бейнесі деп аталады.
Кез келген жиынды өзіне-өзін бірмәнді етіп бейнелеу, бейнелеулердің көбейтіндісіне қатысты топ құрайды.
Анықтама.
Егер G тобын
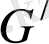 тобына бейнелеуде
тобына бейнелеуде
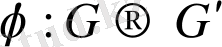 топтық операция сақталатын болса, онда бейнелеу гомоморфты деп аталады, яғни кез келген a, b
топтық операция сақталатын болса, онда бейнелеу гомоморфты деп аталады, яғни кез келген a, b
 G үшін
G үшін
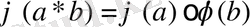 орындалады.
орындалады.
Гомоморфизм топтық операцияны ғана емес, бірлік және кері элементтерді де сақтайды.
Гомоморфты бейнелеудің қасиеттері:
- Гомоморфты бейнелеуде G тобының бейтарап элементітобының бейтарап элементіне бейнеленеді.
- G тобының өзара кері элементтерітобының өзара кері элементтеріне бейнеленеді.
Анықтама. Биективті гомоморфизм топтың изоморфизмі деп аталады . пы.
Анықтама.
 тобы G тобының
изоморфты бейнесі
деп аталады, егер топтық оперцияны сақтайтын, өзара бірмәнді
тобы G тобының
изоморфты бейнесі
деп аталады, егер топтық оперцияны сақтайтын, өзара бірмәнді
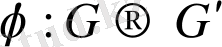 бейнелеуі табылса, яғни:
бейнелеуі табылса, яғни:
1. егер a, b - G тобының әртүрлі элементтері болса, онда
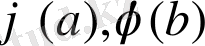 -
-
 тобының әртүрлі элементтері;
тобының әртүрлі элементтері;
2.
 тобының әрбір
тобының әрбір
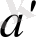 элементі үшін,
элементі үшін,
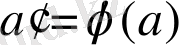 орындалатындай, G тобынан а элементін табуға болады;
орындалатындай, G тобынан а элементін табуға болады;
3. егер
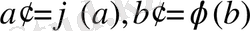 және
және
 , онда
, онда
 . Сонымен, егер гомоморфты бейнелеу
. Сонымен, егер гомоморфты бейнелеу
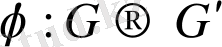 өзара бірмәнді болса, онда ол
изоморфты
деп аталады, ал G және
өзара бірмәнді болса, онда ол
изоморфты
деп аталады, ал G және
 топтары
изоморфты топтар
деп аталады. Белгіленуі:
топтары
изоморфты топтар
деп аталады. Белгіленуі:
 .
.
Қасиеттері:
1) Рефлексивті.
2) Симметриялы.
3) Транзитивті.
3. Сақина, сақинаның мысалдары. Қарапайым қасиеттері. Ішкі сақиналар. Бүтін сандар сақинасы. Сақиналардың гомоморфтылығы және изоморфтылығы. Өріс. Рационал сандар өрісі.
Анықтама.
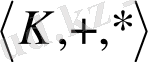 алгебрасы, яғни екі бинарлық алгебралық операциясы бар бос емес жиын сақина деп аталады, егер келесі аксиомаларды қанағаттандырса:
алгебрасы, яғни екі бинарлық алгебралық операциясы бар бос емес жиын сақина деп аталады, егер келесі аксиомаларды қанағаттандырса:
1)
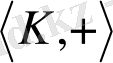 - абельді топ;
- абельді топ;
2)
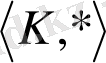 - жартылай топ;
- жартылай топ;
3) «+», «*» амалдары дистрибутивті заң арқылы байланысқан
болса.
Анықтама.
Егер
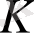 сақинасында «*» амалы бойынша коммутативті заң орындалса, онда
сақинасында «*» амалы бойынша коммутативті заң орындалса, онда
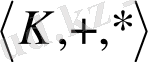 сақинасы коммутативті сақина деп аталады.
сақинасы коммутативті сақина деп аталады.
Анықтама.
Егер
 ,
,
 үшін
үшін
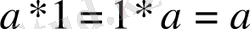 орындалса, онда
орындалса, онда
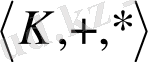
сақинасы бірі бар сақина деп аталады.
Мысалдар.
- <{0}, +, > - нөлдік сақина.
- <, +, >- коммутативті бірі жоқ сақина.
- <, +, > - nайнымалылы нақты коэффициентті көпмүшеліктер жиынының сақинасы.
- <(R), +, > - n-ші ретті шаршылы матрицалар сақинасы, элементтері R жиынынан.
- <, +, > - mмодульды қалындылар класының сақинасы, бірі бар коммутативті сақина.
- - бүтін сандар жиынының қосу, көбейту амалдарына қатысты сақина екендігін дәлелдеп көрейік.
І
 - абельді топ.
- абельді топ.
1.
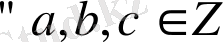 үшін
үшін
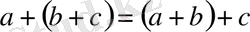 ассоциативтілік орындалады.
ассоциативтілік орындалады.
2.
 ,
,
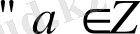 үшін
үшін
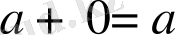 бейтарап элемент табылды.
бейтарап элемент табылды.
3.
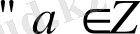 үшін
үшін
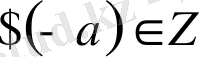
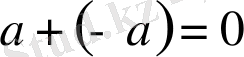 - кері элемент табылды.
- кері элемент табылды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz