Серпімділік теориясы: кернеу және деформация тензорлары, кернеу шоғырлануы және пластикалық ағымның теориялық негіздері


Тема № 1. Серпімділік теориясы. Деформациялар мен кернеулерлің тензорлары.
Қатты дене механикасының негізгі бағыттары - қирау механизмдері мен деформациялау процестерін зерттеу. Деформацияланатын дене беріктігінің бұзылуы шамадан тыс деформациялау, жұмыс тұрақтылығының бұзылуына байланысты. Қирау ол пластикалық, сынғаннан, тозғаннан, серпілістен және шірігеннен болуы мүмкін. Көптеген жағдайларда кернеу шоғырланған орындарында бұзылу жүреді. Серпімді денеде кернеудің шоғырлануы негізінен басты екі механизмнің әсерінен пайда болуы мүмкін: тесік сияқты немесе оның геометрия бетінің күрт өзгеруі, дененің геометриялық бөліктері және денеге әсер етуші шоғырланған күштер. Кернеулердің шоғырлануынан туындаған жергілікті кернеуді ұлғайту кей жағдайларда құрылымдардағы бастамашылық тозудан пайда болатын жарықтарын туғызады, ол инженерлік жобалауда мұқият зерттелген болуы тиіс. Сыртқы күштер үшін серпімді денеде кернеу шоғырлану мәселелерін, сондай-ақ құрылымдық бөліктер үшін, айналма және эллиптикалық ойықтар сияқты, кешенді потенциалдар және Эрб кернеу функцияларын пайдалана отырып шешіледі. Осы зерттеу жұмыстарында денелерде серпімділік мәселелерінде шегінен тыс кернеулердің шоғырлануына, қарастырылған икемділік теориясы арасындағы тек серпімді ара-қатынастар бағынбайтын және онда пластикалық деформациялар дами бастауына басты назар аударылды. Серпімділік теориясы осы деңгейге дейінгі кернеуге ұшырайтын бүкіл жүктемені жойғаннан кейін қалатын деформацияға алып келетін механикалық қатты денелермен байланысты. Теория Француз Академиясының эксперименттері туралы Г. Треска хабарлағаннан кейін 1864 жылы пайда болған, бұл жерде қашан максималды кернеудің ығысуы толық деңгейге жеткенде металл созылғыштығы басталады деп болжады. Осыдан кейін математик Б. Сен-Венан пластикалық ағымы мәселелерін қарастырды және негізгі екі өлшемді теңдеулерді дайындады, оны 1871 М. Леви жылы үш өлшемді теңдеуілер қорытындылаған. Р. Мизес осы мәселе бойынша өз зерттеулерін жариялағанша, 1913 жылға дейін теория ешқандай елеулі табыстарға қол жеткізбеді. Пластикалық шартпен бірге Треска1856 жылы Максвелмен ұсынылған, серпімді энергияның шартындағы эквивалентен және аққыштықты өлшеу эксперименттері сипатталған Треска критерийіне алып келетін аққыштықтың математикалық критерийлерін ұсынды. Бүгінде пайдаланылатын созылу теориясының негізін Л. Прандтл 1924 ж. және Э. Рейс 1930 ж. бірге қорытындылаған, бұл теорияны ағымының теңдеулері деформациялардың серпімді қоспалардың құрайды. 2 Қазіргі серпімділік теориясын екі негізгі топқа бөлуге болады. Бірінші топтағылар деформациялық деп аталатын теориялар, Гук заңының біржақты кернеулік күйіне бағынатын деформациялық және кернеулікке байланысты сипаттарын белгілейді. Екінші топта шексіз шағын қадамдар деформациялар мен кернеулер арасындағы байланысты, сондай-ақ өздері кернеулермен қаралады. Өсім деформация орнына деформация жылдамдығын енгізуге болады, егер кернеу параметрдің өсіп келе жатқан кадамдарына тәуелділігін өзгертсе және бұл уақыт параметр деп саналсын, бұл уақыттың ауқымдығының ешқандай маңызы болмайды. Бұл теорияларда пластикалық деформация пластикалық ағымы материалының процесі ретінде қарастырылады. Сондықтан, олар теориялық ағым деп аталады
Тұтас орта механикасында ортаның кез келген нүктесінде кернеулік-деформацияланған күйі үш бір-біріне перпендикулярлы алаңшалардағы тоғыз кернеулер мен тоғыз деформациялар компоненттерімен толық анықталады. Кернеулер компоненттері болып үш қалыпты кернеулер ( σ x , σ y , σ z ) мен бір- біріне тең жанама кернеулердің үш жұбы (τ x = τ yx . . . ) ал деформациялар компоненттері болып - үш сызықты деформациялар ( ξ 1 , ξ 2 , ξ 3 ) мен бір-біріне тең бұрыштық (жылжу) деформациялардың үш жұбы (γ xy = γ yx , . . . ) танылады.
Ортаның нүктесіндегі кернеулік күй
 (1)
(1)
кернеулер тензорымен сипатталады, ал деформацияланған күй
 (2)
(2)
деформациялар тензорымен айқындалады.
Егер де (1) кернеулер тензоры мен (2) деформациялар тензорын бас біліктерге (осьтерге) жатқызсақ, онда оларды келесі түрде келтіруге болады:
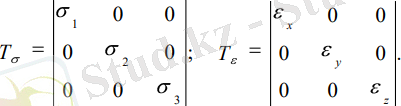 (3)
(3)
Қолданылған әдебиеттер
- Савельев И. В. Жалпы физика курсы. т. 1, 2, 3, Алматы, Мектеп, 1977
- 2. Трофимова Т. И. Курс физики, М., Высшая школа, 1985ж.
- Зисман Г. А. Тодес О. М. Курс общей физики. Т. 3. - М: Наука, 1970
- Яворский Б. М. и другие. Курс физики. Т-3. - М: Высшая школа. 1964-1973
Детлав А. А., Яровский В. М., Милковская Л. В. Курс физики. т. 2, 3. М., Высшая школа, 1877
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz