Оң таңбалы сандық қатарлар: негізгі ұғымдар, жинақталу шарттары және салыстыру теоремалары


Реферат
Тақырыбы: Оң таңбалы қатарлар.
Дайындаған:
Оқу тобы:
Қабылдаған:
Мазмұны
Кіріспе.
1. Сандық қатарлар туралы негізгі ұғым. Негізгі теоремалары.
1. 1. Сандық қатарлар туралы негізгі ұғым.
1. 2. Негізгі теоремалар.
2. Қатар жинақтылығының қажетті шарты. 3. Мүшелері оң қатарлар. Қатарларды салыстыру белгісі.3. 1. Мүшелері оң қатарлар.
4. 2. Қатарларды салыстыру белгісі.
Қорытынды.Қолданылған әдебиеттер тізімі.
Кіріспе
Философия тарихында бір адамның қызметі мен шығармашылығы дәуірлейтін ғылыми жаңалықтар мен тарихи-философиялық процестің негізін қалайтын ең терең философиялық идеялармен үйлесетін мысалдар көп емес. Осындай ойшылдардың ішінде ұлы неміс философы және ғалымы Готфрид Вильгельм Лейбниц ерекше көзге түседі.
Оның өмірі Еуропалық тарихтың жаңа кезеңі деп аталатын кезеңде өтті, оны әдетте ағылшын философиясы, буржуазиялық революция оқиғалары ашады, ол болашақ философ дүниеге келерден бірнеше жыл бұрын басталды және ол философиялық көзқарастардың қалыптасқан жүйесімен жетілген ойшыл болып қалыптасқан жылдары аяқталды.
Лейбництің отаны болған Германия әлеуметтік-экономикалық және саяси дамуы жағынан сол кезде ең дамыған капиталистік елге айналған Англиядан ғана емес, Нидерланды мен Франциядан да төмен болды. Сол ғасырдағы Германияға тән феодалдық-асыл жүйе, ауылшаруашылық экономикасының қалалық, сауда, қолөнер және өнеркәсіптік экономикадан басым болуы. Оның тарихи дамуына кедергі болған маңызды фактор саяси бытыраңқылық болды. Ел көлемінен, экономикалық, саяси және әскери күштерінен ерекшеленетін жүздеген мемлекеттік құрылымдардан тұрды. Бүкіл Германия үшін жарамды тиімді орталықтандырылған үкімет болған жоқ, дегенмен жекелеген сайлаушыларда, герцогтықтар мен қалаларда мұндай билік құрылды және нығайтылды.
17 ғасырдағы Германияның саяси және экономикалық бытыраңқылығының экономикалық себептерін талдауға кіріспестен, әр түрлі мемлекеттерде католиктік және протестанттық (негізінен лютерандық формада) діндер болған осы елдің діни біртектілігін атап өту керек. Діннің сол дәуірдегі халықтардың рухани өміріндегі рөлі, әртүрлі саяси қозғалыстар, жоспарлар мен есептеулер көбінесе шешуші болды. Тіпті экономикалық мүдделер көбіне сол кезде діни тұрғыда қабылданды. Ағылшын буржуазиялық революциясы діни ұрандар мен баннерлер астында өтті. Германияны күйретіп, оның экономикалық артта қалуы мен саяси бытыраңқылығына ықпал еткен қатал отыз жылдық соғыс (1618-1648), оған қатысушылардың санасында католиктер мен протестанттар арасындағы діни соғыс болып көрінді.
Осы тақырып бойынша бірқатар зерттеулермен таныса отырып, мен Готфрид Вильгельм Лейбниц туралы көбірек білгім келді. Ол ұлы неміс философтарының алғашқысы болды. Лейбниц сонымен қатар неміс философиясының белгілерінің біріне айналған жан-жақты философиялық жүйені ұсынған отандастарының алғашқысы болды.
Сандық қатарлар туралы негізгі ұғым. Негізгі теоремалары
- Сандық қатарлар туралы негізгі ұғым.
- Негізгі теоремалар.


Айталық бізге { U n } сандық тізбегі берілсін. Осы тізбектің элементтерінен
 U
1
U
2
U
1
U
2
. . . U n
. . .
(1)
түріндегі өрнек түзейік. Бұл өрнекті сандық қатар немесе жай ғана қатар деп атайды.
Қатарды жиі U n
n 1
түрінде жазады, мұнда n индексінің барлық 1, 2, 3, . . . натурал сандарын
қабылдайтыны көрсетілген. U 1, U 2, . . . , U k , . . . сандарын қатардың мүшелері деп, ал қатардың белгілі бір орнында тұрған, мысалы, басынан бастағанда n-ші орында тұрған мүше, яғни
U n , қатардың n-ші мүшесі деп аталады. Ал егер n үшін кез келген сан алынса, онда U n
қатардың жалпы мүшесі деп аталады. Егер қатарды түзетін { U n } тізбегі берілсе, онда қатарды берілген деп есептейді, яғни қатарды берілген деп есептейді, егер оның жалпы мүшесі берілсе, әдетте, жалпы мүше формула арқылы беріледі. Мысалы, қатардың жалпы
мүшесі U
( 1) n 1
62 n 1
формуласы арқылы берілсе, онда қатар түрі былай
n (2 n
1) !
3 5 7


n 1 2 n 1


 6
6
6
6
6 6
. . .
( 1) 6
3! 5! 7!
n 1 (2 n
1) !
болады.
Берілген қатардың алғашқы n мүшелерінің қосындысын осы қатардың n-ші дербес

 қосындысы деп атайды да,
S n
қосындысы деп атайды да,
S n
арқылы белгілейді. Сонымен,

S n U 1 U 2
. . .
U n , (2)




 Егер n-ге тізбектей 1, 2, 3, . . . мәндерін берсек,
Егер n-ге тізбектей 1, 2, 3, . . . мәндерін берсек,
S 1 U 1, S 2
U 1 U 2, S 3
U 1 U 2
U 3,
. . .
(3)
дербес қосындылар { S n
} тізбегін аламыз.
Егер { S n
} дербес қосындылар тізбегінің S= lim S n
n
арқылы шегі бар болса, онда (1)


 жинақты немесе жинақталатын қатар деп, ал S шегі (1) қатардың қосындысы деп аталады және
жинақты немесе жинақталатын қатар деп, ал S шегі (1) қатардың қосындысы деп аталады және
S n = U 1 U 2
. . . U n
. . .
немесе
S= U n
n 1
деп жазады.
Егер дербес қосындылар { S n
} тізбегінің шегі жоқ немесе ±∞ және ∞ болса, онда
(1) қатар жинақталмайтын немесе жинақсыз қатар деп аталады. Керісінше,
S 1, S 2, . . . , Sn , . . .
(4)







 сандық тізбегінің жинақтылық немесе жинақсыздық мәселесін
сандық тізбегінің жинақтылық немесе жинақсыздық мәселесін
 S
1 (
S
2
S
1 (
S
2
S 1 )
( S 3
S 2 )
. . .
( Sn Sn 1 )
. . .
(5)
қатарының жинақтылық немесе жинақсыздық мәселесіне келтіруге болады.
Шынында да, (5) қатардың n-ші дербес қосындысы
S n , яғни (4) тізбектің n-ші
мүшесіне тең, демек, бұл тізбектің шегінің бар болуы (5) қатардың қосындысының бар болуымен тең мағыналы.


Мысалы, геометриялық прогрессия элементтерінен түзілген

 1
q q
2
1
q q
2
. . . q n
. . .
q n 1
n 1
(6)
қатарын қарастырайық. Мұның S n
дербес қосындысы q ≠1 болғанда
S 1 q
. . .
q n 1
1 q n 1 q n
(7)

n 1 q
1 q 1 q
Егер q<1 болса, онда (6) қатар жинақты, өйткені дербес қосындылар тізбегінің шегі 1 .
1 q
Ал q>1 болса S n
жинақсыз, демек, (6) қатар жинақсыз.
Енді q=1 болса, онда егер q=1 болса, q=-1 болса, онда (6) қатар
1-1+1-1+ . . . = (
n 1
S n =n, демек, S n
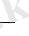 1)
n
1
1)
n
1
тізбегінің жинақсыздығы айқын, ал (8)



 түрінде болады. Мұның дербес қосындылары
түрінде болады. Мұның дербес қосындылары
S 1 1,
S 2 0
, . . . ,
S 2 n 1 1,
S 2 n
0, … тізбегінің шегі жоқ, демек, (8) қатар
жинақсыз.
Қатар жинақтылығының қажетті шартыЕгер (1) қатар жинақты болса, онда нөмірінің шексіз өсуінде оның жалпы мүшесі
нөлге ұмтылуы, яғни
lim U n =0 болуы қажетті.
n
Айталық, (1) қатар жинақты және S оның қосындысы болсын, яғни
lim S n =S. Бұл
n
теңдік, n→+∞ шартында орындалған, демек, мұнымен бірге
lim
( n 1)
S n 1 =S теңдігі де
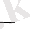
орынды, ал ол lim S n 1 =S шартымен тең мағыналы. Ал U n = S n - S n 1, демек,
n
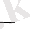
lim U n = lim ( S n - S n 1 ) = lim S n - lim S n 1 =S-S=0.
n n n n
Сонымен, (1) қатардың жинақтылығы үшін оның жалпы мүшесінің шегі бар және нөлге тең болуы қажетті екен.
Ескерт у. Егер
lim U n =0 болса, онда мұнан (1) қатардың жинақтылығы шыға
n
бермейді, яғни бұл шарт қатар жинақтылығы үшін жеткілікті емес.
Мысалы, гармониялық қатар деп аталатын
1 1 1
2 3
. . .
1 . . .
n
(11)
қатарының жалпы мүшесі
1 →0, n→∞, бірақ ол жинақталмайды.
n
Шынында да,
1
S n =1
2
1 . . . 1,
3 n
S 2 n
1 1 . . . 1
2 n
1 . . .
n 1
1 1
2 n 1 2 n
дербес қосындыларын алып, егер (11) жинақты десек, онда
S 2 n →S, n→∞, болар еді. Сөйтіп,
S n →S, n→∞, сонымен бірге
lim ( S 2 n - S n ) = lim S 2 n - lim S n =S-S=0
n n n
болуы керек. Бірақ
1
S 2 n - S n =
n 1
1 . . .
n 2
1 1
2 n 1 2 n
1 1
2 n 2 n
. . . 1 n 1 1
2 n 2 n 2
яғни
1
S 2 n - S n ≥
2
. Мұнан
lim ( S 2 n - S n ) ≠0, бұл гармониялық қатардың жинақталады деген
n
тұжырымына қайшы, демек, гармониялық қатар жинақты емес.
Салдар. Егер (1) қатардың жалпы мүшесі нөмірінің шексіз өсуінде нөлден өзгеше шегі бар немесе шегі жоқ болса, онда қатар жинақталмайды.
Мысалы, 1
2
2 . . .
3
n . . . қатары жинақсыз, өйткені
n 1
n
lim U n = lim
=1≠0.
n n n 1
- қатардың алғашқы n мүшелерін лақтырып тастағаннан пайда болған
U n 1
U n 2
. . .
U n k
. . . rn
(12)
қатарын (1) қатардың қалдығы немесе (1) қатардың n-ші қалдығы деп атайды.
- -т еорема. Қатар мен оның қалдығының екеуі де бірге жинақты немесе екеуі де бірге жинақсыз.
Дәлелдеуі. Айталық S n
(1) қатардың алғашқы n мүшелерінің қосындысы, ал
S k ′










 (12) қалдық қатардың алғашқы k мүшелерінің қосындысы болсын. Онда
(12) қалдық қатардың алғашқы k мүшелерінің қосындысы болсын. Онда
немесе
S k ′= U n 1
U n 2
. . .
U n k =( U 1 U 2
. . .
U n k ) -( U 1 U 2
. . .
U n )
 мұнан
мұнан
S k ′= Sn k - S n , (13)
Sn k = S k ′+ S n
(14)
Егер (1) қатар жинақты, яғни
lim S k =S деп ұйғарсақ, онда
k
lim Sn k =S, өйткені
k
k→+∞, онда (n+k) →+∞. Сонда (13) -теңдіктен
lim
S k ′= lim ( Sn k - S n ) = lim Sn k - lim S n =S- S n ,

k k k k
яғни (12) қатардың дербес қосындысының шегі бар және ол S- S n , ал бұл (12) қатардың жинақты екенін көрсетеді.
Енді (12) қатар жинақты және
lim
k
S k ′=S′ болсын. Онда (14) -теңдіктен
lim Sn k = lim ( S k ′+ S n ) = lim S k ′+ lim S n =S′+ S n ,
k k k k
 яғни қатардың жинақты.
яғни қатардың жинақты.
Sn k
дербес қосындысының шегі бар және ол S′+ S n , демек, (1) қатар
Егер (1) және (12) қатарлардың біреуі жинақталмаса, онда екіншісі де
жинақталмайды, өйткені дәлелдеуіміз бойынша екіншісі жинақты болса, онда біріншісі де жинақты болған болар еді.
Салдар. Егер екі қатардың тек бірнеше мүшелері ғана бір-бірінен өзгеше болса, онда бұл қатарлар бірге жинақты немесе бірге жинақсыз.


Дәлелдеу. Шынында да, егер
 U
1
U
2
U
1
U
2
. . . U n
. . .
(15)
және

V 1 V 2 V 3

. . . Vn
. . .
(16)
қатарларының n> k нөмірінен бастап мүшелері
U n = Vn
болса, онда (15) және (16)
қатарлары (12) қатармен бірге жинақты немесе жинақсыз болады.
Ескерт у. Сонымен, қатарға бірнеше мүше қосқаннан және одан бірнеше мүше алып тастағаннан оның жинақтылығы өзгермейді. Өйткені бірнеше мүшені лақтырып тастауды салдардың дербес жағдайы деп қарастыруға болады, дәлірек айтсақ, бірнеше мүшесін нөлмен ауыстыру деп есептеуге болады.
- -т еорема. Егер жинақты қатардың әрбір мүшелерін бір тұрақты санға көбейткеннен қатар жинақты және оның қосындысы да сол тұрақты көбейткіш көбейтіндісіне тең.


Дәлелдеу. (1) қатардың әрбір мүшесін С тұрақты санына көбейтіп,
 CU
1
CU
1
CU 2
. . .
CU n
. . .
(17)

 қатарын алып, оның
қатарын алып, оның

 Qn CU
1
Qn CU
1
CU 2
. . .
CU n
 n-ші дербес қосындысын түзейік. Ақырлы қосынды қасиеті бойынша
n-ші дербес қосындысын түзейік. Ақырлы қосынды қасиеті бойынша


 Qn C
(
U
1
U
2
Qn C
(
U
1
U
2
. . .
U n ) .
Мұндағы жақшадағы өрнек (1) қатардың n-ші дербес қосындысы
S n . Сондықтан
Qn CS n . Ал (1) қатар жинақты, демек,
lim S n =S. Сонда
lim Qn = lim С S n =С lim S n =СS
n n n n
бар. Сондықтан (17) жинақты әрі оның қосындысы Q=СS. Сонымен, жинақты қатарлар, ақырлы қосындылар сияқты көбейтудің дистрибутивтік заңына бағынышты екен.
Мүшелері оң қатарлар. Қатарларды салыстыру белгісі
- Мүшелері оң қатарлар.
- Қатарларды салыстыру белгісі.
Егер қатардың барлық мүшелері теріс емес болса, онда мұндай қатар мүшелері теріс емес қатар деп аталады.


1-т еорема. Мүшелері теріс емес қатар, яғни
 U
1
U
2
U
1
U
2
. . . U n
. . . , U k ≥0, k=1, 2, . ., n, . . . (18)
қатары жинақты болуы үшін оның дербес қосындылар тізбегінің жоғарыдан шектеулі болуы қажетті және жеткілікті.
Дәлелдеу. Ж ет кілікт ілігі. Айталық (18) қатардың дербес қосындылар тізбегі
S 1, S 2, . . . , S k , . . .
(19)

 жоғарыдан шектеулі болсын. Ал (18) қатардың мүшелері теріс емес болғандықтан,
S n
1 =
S n
+
U n
1 ≥
S n
, яғни (19) дербес қосындылар тізбегі монотонды кемімейді және ол жоғарыдан шектелген, демек, тізбектің ақырлы шегі бар, сондықтан (18) қатар жинақты.
жоғарыдан шектеулі болсын. Ал (18) қатардың мүшелері теріс емес болғандықтан,
S n
1 =
S n
+
U n
1 ≥
S n
, яғни (19) дербес қосындылар тізбегі монотонды кемімейді және ол жоғарыдан шектелген, демек, тізбектің ақырлы шегі бар, сондықтан (18) қатар жинақты.
Қажет т ілігі. Айталық (18) қатар жинақты. Онда анықтама бойынша (19) тізбектің
S ақырлы шегі бар. Демек, { S n }-шектеулі, дербес жағдайда жоғарыдан шектеулі.
Мүшелері теріс емес қатарлар жинақтылығының салыстыру белгілері.1-т еорема. Айталық барлық n нөмірлері үшін
U n және Vn
n 1 n 1
- мүшелері теріс емес екі қатары беріліп,
U n ≤ Vn
(20)
теңсіздігі орындалсын. Онда Vn
n 1
қатарының жинақтылығынан
U n қатарының
n 1
жинақтылығы, ал U n
n 1
шығады.
қатарының жинақсыздығынан Vn
n 1
қатарының жинақсыздығы
Дәлелдеу. U n n 1
және Vn
n 1
қатарларының n-ші дербес қосындыларын сәйкес
S n және Qn
арқылы белгілейік. Онда (20) теңсіздіктен
S n ≤ Qn
(21)
теңсіздігі шығады. Vn
n 1
қатары жинақты және Q оның қосындысы болса, онда
Qn ≤Q
теңсіздігін, ал (21) теңсіздіктен
аламыз, яғни U n n 1
S n ≤Q (22)
қатарының дербес қосындылар тізбегі жоғарыдан Q санымен
шектелген, демек, U n
n 1
қатары жинақты.
Енді теореманың екінші жартысын дәлелдейік. U n
n 1
қатарының { S n } дербес
қосындылар тізбегінің шектеусіздігінен Vn
n 1
шектеусіздігі шығады.
қатарының дербес қосындылар тізбегі { Qn }
- -ескерт у. Бұл теоремада (20) теңсіздік барлық n нөмірлері үшін емес тек белгілі бір нөмірден бастап орындалса болғаны, өйткені саны ақырлы мүшелерін лақтырып тастағаннан қатар жинақтылығы өзгермейді.
- -ескерт у. Жоғарыдағы теоремада (20) теңсіздік орнына
U n ≤С Vn
(С-тұрақты) (23)
теңсіздігін алуға болады. Өйткені
Vn қатарының жинақталуы мен
n 1
CVn
n 1
қатарының
жинақталуы тең мағыналы әрі мұнда да (23) теңсіздікті белгілі бір нөмірден бастап орындалсын деп ұйғаруға болады.
Егер қатардың барлық мүшелері нөлден қатаң үлкен болса, онда қатар мүшелері қатаң оң қатар деп аталады.
Салдар. Егер болып және
U n - мүшелері теріс емес, ал
n 1
U
lim n =L,
Vn -мүшелері қатаң оң қатарлар
n 1
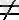 ,
,
L 0
V
n
n
ақырлы шегі бар болса, онда
Vn қатарының жинақтылығынан
n 1
U n қатарының
n 1
жинақтылығы, ал U n
n 1
шығады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz