Оң таңбалы қатардың жинақтылық белгілері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

Реферат

Тақырыбы: Оң таңбалы қатардың жинақтылық белгілері.

Дайындаған:

Оқу тобы:

Қабылдаған:

Мазмұны

1. Мүшелері оң қатарлар. Қатарларды салыстыру белгісі. 2. Ауыспалы таңбалы қатарлар қатарлардың абсолютті жинақталуы 3. Қатардың абсолютті жинақталуының қасиеттері Қорытынды.

Қолданылған әдебиеттер тізімі.

МҮШЕЛЕРІ ОҢ ҚАТАРЛАР. ҚАТАРЛАРДЫ САЛЫСТЫРУ БЕЛГІСІ.

Дәрістің мақсаты: Мүшелері оң қатардың анықтамасы, оның дербес қосындыларының қасиеттері мен қатардың жинақтылығының байланысын білу. Оң мүшелі қатардың жинақталуының салыстыру белгісін дәлелдей және практикалық сабақта қолдана білу.

Мүшелері оң қатарлар.
Қатарларды салыстыру белгісі.

Егер қатардың барлық мүшелері теріс емес болса, онда мұндай қатар мүшелері теріс емес қатар деп аталады.

1-т еорема. Мүшелері теріс емес қатар, яғни

U 1 U 2

. . . U n

. . . , U k ≥0, k=1, 2, . ., n, . . . (18)

қатары жинақты болуы үшін оның дербес қосындылар тізбегінің жоғарыдан шектеулі болуы қажетті және жеткілікті.

Дәлелдеу. Ж ет кілікт ілігі. Айталық (18) қатардың дербес қосындылар тізбегі

S 1, S 2, . . . , S k , . . .

(19)

жоғарыдан шектеулі болсын. Ал (18) қатардың мүшелері теріс емес болғандықтан, S n 1 = S n + U n 1 ≥ S n , яғни (19) дербес қосындылар тізбегі монотонды кемімейді және ол жоғарыдан шектелген, демек, тізбектің ақырлы шегі бар, сондықтан (18) қатар жинақты.

Қажет т ілігі. Айталық (18) қатар жинақты. Онда анықтама бойынша (19) тізбектің

S ақырлы шегі бар. Демек, { S n }-шектеулі, дербес жағдайда жоғарыдан шектеулі.

Мүшелері теріс емес қатарлар жинақтылығының салыстыру белгілері.

1-т еорема. Айталық барлық n нөмірлері үшін

U n және Vn

n 1 n 1

- мүшелері теріс емес екі қатары беріліп,

U n ≤ Vn

(20)

теңсіздігі орындалсын. Онда Vn

n 1

қатарының жинақтылығынан

U n қатарының

n 1

жинақтылығы, ал U n

n 1

шығады.

қатарының жинақсыздығынан Vn

n 1

қатарының жинақсыздығы

Дәлелдеу. U n n 1

және Vn

n 1

қатарларының n-ші дербес қосындыларын сәйкес

S n және Qn

арқылы белгілейік. Онда (20) теңсіздіктен

S n ≤ Qn

(21)

теңсіздігі шығады. Vn

n 1

қатары жинақты және Q оның қосындысы болса, онда

Qn ≤Q

теңсіздігін, ал (21) теңсіздіктен

аламыз, яғни U n n 1

S n ≤Q (22)

қатарының дербес қосындылар тізбегі жоғарыдан Q санымен

шектелген, демек, U n

n 1

қатары жинақты.

Енді теореманың екінші жартысын дәлелдейік. U n

n 1

қатарының { S n } дербес

қосындылар тізбегінің шектеусіздігінен Vn

n 1

шектеусіздігі шығады.

қатарының дербес қосындылар тізбегі { Qn }

-ескерт у. Бұл теоремада (20) теңсіздік барлық n нөмірлері үшін емес тек белгілі бір нөмірден бастап орындалса болғаны, өйткені саны ақырлы мүшелерін лақтырып тастағаннан қатар жинақтылығы өзгермейді.
-ескерт у. Жоғарыдағы теоремада (20) теңсіздік орнына

U n ≤С Vn

(С-тұрақты) (23)

теңсіздігін алуға болады. Өйткені

Vn қатарының жинақталуы мен

n 1

CVn

n 1

қатарының

жинақталуы тең мағыналы әрі мұнда да (23) теңсіздікті белгілі бір нөмірден бастап орындалсын деп ұйғаруға болады.

Егер қатардың барлық мүшелері нөлден қатаң үлкен болса, онда қатар мүшелері қатаң оң қатар деп аталады.

Салдар. Егер болып және

U n - мүшелері теріс емес, ал

n 1

U

lim n =L,

Vn -мүшелері қатаң оң қатарлар

n 1

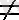L 0

ақырлы шегі бар болса, онда

Vn қатарының жинақтылығынан

n 1

U n қатарының

n 1

жинақтылығы, ал U n

n 1

шығады.

қатарының жинақсыздығынан Vn

n 1

қатарының жинақсыздығы

Дәлелдеу. Шек анықтамасынан

U

lim n =L дегеніміз анықтама бойынша: кез

n

келген ε>0 саны үшін Ν нөмірі табылып, n≥Ν болғанда

L-ε≤ U n ≤ L+ε,

яғни n≥Ν болғанда

U n ≤(L+ε) Vn

теңсіздігі орынды, ал бұл теңсіздік С=L+ε десек (23)

теңсіздігімен бірдей, демек, 2-ші ескерту бойынша салдар дәлелденді.

2-т еорема. Айталық

нөмірлері үшін

U n және

n 1

Vn -мүшелері қатаң оң екі қатар және барлық n

n 1

U n 1

U n

Vn 1

Vn

(24)

теңсіздігі орындалсын. Онда Vn

n 1

қатарының жинақтылығынан U n

n 1

қатарының

жинақтылығы, ал U n

n 1

шығады.

қатарының жинақсыздығынан

Vn қатарының жинақсыздығы

n 1

Дәлелдеу. (24) теңсіздікті n=1, 2, . ., k-1 үшін жазсақ

U 2 V 2, U 3

U 1 V 1 U 2

V 3, . . . ,

V 2

U k

U k 1

Vk .

Vk 1

Бұл теңсіздіктерді мүшелеп көбейтсек,

U 1 теңсіздігін аламыз. Мұндағы

1

U V

k k

U 1 =С

V 1

көбейткіші оң және k-ден тәуелсіз тұрақтыны анықтайтын болғандықтан, жоғарыдағы 2- ескертуден теорема дәлелдеуін аламыз.

-ескерт у. Бұл теорема шартын да белгілі бір нөмірден бастап айтуға болады.

Бұл теоремаларды салыстыру теоремалары немесе салыстыру белгілері деп атайды.

Мысалы, 1.

n 1 5

1, a>0, қатарын жинақтылыққа зерттейік. Егер а≤1 болса, онда

a n

n-ші мүше n→∞ ұмтылғанда нөлге ұмтылмайды, демек, қатар жинақты емес. Егер а>1

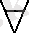болса, онда n үшін

1 1

теңсіздігі орынды және

1 қатары жинақты, демек,

берілген қатар жинақты.

n n n

n 1

2. 1

a a

n 1 n

1 1 . . . 1

2 n

. . . , α≤1, (25)

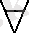қатарын жалпыланған гармониялық қатар деп атайды. Ал α≤1 болғанда n үшін 1 1

n n

теңсіздігі орынды және

n 1 n

гармониялық қатары жинақсыз, демек (25) қатар жинақсыз.

3. 1

n 1

cos

қатарын жинақтылыққа зерттейік. Ол үшін 1

cos

2sin2

2 n 2 n

екенін және оның аргументі

-нің n шексіздікке ұмтылғанда нөлге ұмтылатынын

2 n

байқап, тамаша шекті пайдаланып,

lim

cos

lim

2 sin 2

2 n

2 lim

sin

2 n 2

n 2 n

(2 n ) 2

2 1 n

4 n 2 2 n

шегін табамыз.

Жоғарыдағы салдардан зерттеп отырған қатарымыздың жинақты екенін көреміз,

өйткені

1 қатары жинақты.

n 1 n

ҚАТАРДЫ ЖИНАҚТЫЛЫҚҚА ЗЕРТТЕУДІҢ ДАЛАМБЕР БЕЛГІСІ.

Дәрістің мақсаты: Оң мүшелі қатардың жинақтылығы үшін Даламбер белгісін дәлелдей білу. Мүшелері геометриялық прогрессия құрайтын қатардың қасиеттерін қолдана білу. Даламбер белгісін есеп шығаруда қолдана білу.

бастап

Сандық қатар жинақтылығының Даламбер белгісі

1-т еорема. Егер қатар мүшелерінің барлық нөмірлері немесе белгілі бір n нөмірден

U n 1 ≤q<1 ( U n 1 ≥1) (26)

U n U n

теңсіздігін қанағаттандырса, онда U n

n 1

қатары жинақты (жинақсыз) .

Vn 1

Vn 1

Дәлелдеу. үшін Vn q

теңсіздікті былай

( Vn

1) деп алайық . Онда

=q<1 (

Vn Vn

=1) әрі (26)

U n 1 ≤ Vn 1 ( U n 1 ≥ Vn 1 ) (27)

U n Vn

U n Vn

түрінде жазуымызға болады. Ал q n

n 1

қатары (6) қатармен тең, демек, егер q<1 болса

жинақты, егер q=1 болса жинақсыз. Сондықтан салыстыру белгілеріндегі теорема

бойынша (24) теңсіздік U n

n 1

2- т еорема. Егер U n

n 1

шегі

қатарының жинақты (жинақсыз) екенін көрсетеді. қатарының n+1-ші мүшесінің n-ші мүшесіне қатынасының

lim U n 1 l

(28)

n U n

бар және ол l <1 болса, онда

U n қатары жинақты, ал l >1 болса, онда қатар жинақсыз.

n 1

Дәлелдеу. Шек анықтамасы бойынша ε>0 саны үшін N нөмірі табылып, n≥N болғанда

l U n 1 l (29)

U n

Егер l <1 болса, онда l =1-2ε және мұнан l +ε=1-ε болатын ε оң санын табуға болады. Сонда (29) теңсіздіктегі l +ε=1-ε саны алдыңғы теоремадағы q рөлін атқарады. Демек, қатар жинақты. Егер l >1 болса, онда l =1+ε болатын, яғни l -ε=1 болатын ε оң санын табуға болады. Сонда (29) теңсіздіктің сол жағындағы l -ε=1 деп, алдыңғы теорема негізінде қатардың жинақсыз екенін көреміз.

-ескерт у. 1-ші теоремада

U n 1 ≤q<1 теңсіздігін

U n

U n 1 <1 теңсіздігімен ауыстыруға

U n

болмайды. Шынында да біз жоғарыда (11) гармониялық қатардың жинақсыз екенін көрсеткенбіз бірақ ол қатар мүшелері барлық n үшін

n

U n 1 ≤ <1

U n n 1

теңсіздігін қанағаттандырады.

-ескерт у. 2-теоремадаl=1 болса, онда қатар жинақтылығы туралы ештеңе айта алмаймыз, яғниl=1 болғанда Даламбер белгісі «жұмыс істемейді».

Мысалы,

1 қатары үшін l =1, бірақ бұл қатар жинақсыз, ал

1 қатары үшін

n 1 n

де l =1, ал бұл қатар жинақты.

n 1 n

АУЫСПАЛЫ ТАҢБАЛЫ ҚАТАРЛАР. ҚАТАРЛАРДЫҢ АБСОЛЮТТІ ЖИНАҚТАЛУЫ.

Дәрістің мақсаты: Ауыспалы таңбалы қатардың анықтамасын білу. Ауыспалы таңбалы қатардың жинақталуының белгісін дәлелдеп, есеп шығаруда қолдана білу.

Ауыспалы таңбалы қатарлар.
Қатарлардың абсолютті жинақталуы

1-т еорема. Мүшелері кезегімен біресе оң біресе теріс болып келетін таңбасы ауыспалы деп аталатын

n 1

( 1) U n ,

n 1

U n 0, n

1, 2, . . .

(50)

қатары берілсін. Егер

lim U n n

0 және U n

U n 1 0,

n 1, 2, . . .

(51)

болса, онда таңбасы ауыспалы (50) қатар жинақты. Сонымен бірге (50) қатардың кез

келген S n

дербес қосындысы оның S қосындысынан келесі U n 1

мүшесінен кіші шамаға

өзгеше, басқаша айтқанда, rn

қатар қалдығының абсолют шамасы өзінің бірінші

мүшесінің абсолют шамасынан аспайды, яғни

rn S Sn

U n 1

Дәлелдеу. Егер (50) жұп нөмірлі дербес қосындыларын

S 2 k

2 k

( 1) n 1

n 1

қарастырсақ, мұны былай

S 2 k

( U 1

U 2 )

( U 3

U 4 )

. . .

( U 2 k 1

U 2 k ) ,

k 1, 2, . . .

деп

жазып,

S 2 k S 2 k 2

екені, яғни жұп нөмірлі дербес қосындылар тізбегінің өспелі екенін

көреміз. Енді сол

S 2 k

U 1 ( U 2

U 3 )

. . .

( U 2 k 2

U 2 k 1 )

U 2 k ,

k 1, 2, . . .

түрінде, Демек,

S 2 k < U 1, екені, яғни,

S 2 k

тізбегінің жоғарыдан шектеулі екенін көреміз.

lim S 2 k S

(52)

Егер тақ нөмірлі дербес қосындыларды қарастырсақ, олардың да осы S шегіне жинақталатынын көрсетуге болады, шынында да,

S 2 k 1

S 2 k

U 2 k 1

, k 1, 2, . . .

(53)

және (51) шарттан

lim U 2 k 1 =0, демек, (52) мен (53) теңдіктерден

k

lim S 2 k 1 S .

k

(54)

Сонымен, (52) және (54) теңдіктерден lim Sk

S екені шығады.

Енді (50) қатар үшін

S 2 k

S S 2 k 1,

k 1, 2, . . .

(55)

теңсіздіктерінің орындалатынын көрсетейік.

Шынында да, дәлелдеуіміз бойынша өспелі

S 2 k ≤S. Екінші жағынан

S 2 k

тізбегінің шегі S, сондықтан

S 2 k 1

S 2 k 1

( U 2 k

U 2 k 1 )

S 2 k 1,

k 1, 2, . . . ,

яғни

S 2 k 1

тізбегі кемімелі және S осы кемімелі тізбек шегі болғандықтан, S≤ S 2 k 1 .

Сонда (55) теңсіздіктерден

S- S 2 k ≤ S 2 k 1 - S 2 k = U 2 k 1,

S 2 k 1 S

S 2 k 1

S 2 k

U 2 k ,

k 1, 2, . . . ,

ал бұл барлық n= 1, 2, . . үшін S - S n ≤ U n 1 деген сөз.

Ескерт у. Егер таңба кезектесіп өзгеруі мен монотондық бірінші мүшеден емес, тек бірнеше мүшеден соң басталса, онда (51) шарттардың орындалуында қатар жинақты, өйткені қатардың бірнеше мүшесін лақтырып тастаудың оның жинақтылығына әсері жоқ.

Абсолютті жинақталатын қатарлар

Егер қатар мүшелерінің абсолют шамаларынан түзілген

U k (38)

k 1

қатары жинақты болса, онда сандық қатар

Uk

k 1

(1)

абсолютті жинақталатын қатар деп аталады. Егер (1) өзі жинақты да, ал оның мүшелерінің модульдерінен түзілген қатар (38) жинақсыз болса, онда сандық қатар (1) шартты жинақталатын қатар деп аталады.

1-т еорема. Егер (38) қатар жинақты болса, онда (1) қатар да жинақты.

Дәлелдеу. U k

k 1

жинақты қатары үшін Коши критерийі орындалады: кез келген

0 саны үшін N нөмірі табылып, барлық n N және кез келген р натурал саны үшін

n p

U k

k n 1

теңсіздігі орындалады. Сонда n N және бүтін р 1 үшін

n p n p

U k U k

k n 1

k n 1

екені айқын, яғни Uk

k 1

қатары үшін де Коши критерийі орындалған, демек, Uk

k 1

қатары да жинақты. Теорема дәлелденді.

Әдебиеттер: [1], 124-130 б., [2] (2-бөлім) .

ҚАТАРЛАРДЫҢ АБСОЛЮТТІ ЖИНАҚТАЛУЫНЫҢ ҚАСИЕТТЕРІ

Дәрістің мақсаты: Қатардың абсолютті жинақталуының анықтамасын, абсолютті жинақталу белгілерін меңгеру. Абсолютті жинақты қатардың қасиеттері туралы теоремаларды дәлелдей білу.

-т еорема. Абсолют жинақты қатардың мүшелерінің орындарын ауыстырудан пайда болған қатар абсолют жинақты және олардың қосындылары тең.

Дәлелдеу. Айталық

Uk қатары абсолют жинақты, ал

k 1

U j осы қатардың

j 1

мүшелерінің орындарын ауыстырудан пайда болған қатар болсын. Ал Uk

k 1

қосындысын S арқылы белгілейік, яғни

қатарының

S= Uk

k 1

(39)

Алдымен

U j қатарының жинақты және қосындысы S болатынын көрсетейік.

Ол үшін

Uk қатарының дербес қосындыларын Sn, ал

n

U j қатарының дербес

қосындыларын Sj және Ŝ= U k

k 1

, Ŝn = U k k 1

, n=1, 2, . . . , деп белгілейік. Теорема шарты

бойынша табылып

U k қатары жинақты болғандықтан, кез келген ε>0 саны үшін N нөмірі

n N 1

=Ŝ-Ŝn<

, (40)

демек,

S-SN=

n N 1

≤ Un

n N 1

< . (41)

Енді

U j қатарының

j 1

SM дербес қосындысын Uk

k 1

қатарының SN дербес

қосындысына енетін барлық мүшелерін қамтитындай етіп М нөмірін таңдап аламыз. Айталық, j>M және Sj″=Sj′-SN болсын. Онда Sj″ шамасы Sj″ қосындысына енетін қосылғыштар абсолют шамасынан аспайды және бұл қосылғыштар нөмірлері N нөмірінен

артық болғандықтан олардың бәрі де бойынша,

Un

n N 1

қосындысының ішінде, демек, (40)

Sj″≤ Un <

n N 1 2

(42)

Егер j>M болса, онда (41), (42) бойынша

S-Sj′=S-(SN+Sj″) ≤S-SN+Sj″< + =ε

2 2

Бұл

U j =S екенін көрсетеді. Енді

j 1

U j қатарының абсолют жинақты екенін көрсету

қалды. Ал бұл дәлелденген тұжырымды U k

k 1

қатарына қолданудан шыға келеді.

Шынында да, мұның абсолют жинақты екені белгілі, демек, оны мүшелері теріс емес

қатар деп қарастыруға болады. Сондықтан, дәлелдеуіміз бойынша, U j

j 1

қатары

абсолют жинақты және оның қосындысы U k

k 1

қатарының қосындысына тең. Коши

критерийінен тікелей шығатын екі қасиет келтірейік.

-т еорема. ЕгерUk

k 1

қатары абсолют жинақты, ал С-кез келген сан болса, онда

CU k

қатары да абсолют жинақты.

Дәлелдеуі. Тікелей Коши критерийінен шығады, өйткені

n p

CU k

k n

n p

C Uk k n

-т еорема. Егер

Uk және Vk

k 1 k 1

қатарлары абсолют жинақты болса, онда

( Uk Vk ) қатары да абсолют жинақты.

k 1

Дәлелдеуі. Коши критерийі мен

n p n p n p

Uk Vk Uk Vk

k n k n k n