Алгебралық теңсіздіктерді дәлелдеу әдістері және мектеп математикасындағы теңдеулерді шешудегі қолданылуы


Бакенова Салтанат Каирбеккызы
Еңбекшілдер ауданы, Алға негізгі мектебі
математика пәнінің мұғалімі
АЛГЕБРАЛЫҚ ТЕҢСІЗДІКТЕРДІ ДӘЛЕЛДЕУ ЖОЛДАРЫ.
Мектеп математика курсында теңдеулерді шешудің төрт негізгі әдісі қолданылады: көбейткіштерге жіктеу, жаңа айнымалы енгізу, функцияларды байланыстыратын теңдіктен аргументтерді байланыстыратын теңдікке көшу, функциялардың графиктік әдісі. Бұлардан басқа арнаулы әдістері бар. Олар, әрине теңдеулерді негізгі әдістермен шешуде қиын болғанда қолданылады. Бұл жоғарғы математикада белгілі жеті теңсіздіктің теңдеулер шешуге қолданылуын қарастырамыз. Бұлар: Коши, Бернулли, Иенсен, дәрежелік орта теңсіздіктері, Гюйгенс, Коши-Буняковский. Бұл теңсіздіктердің математиканың әр түрлі салаларында, мысалы функционалдық анализде енгізу теоремаларын дәлелдегенде, операторларды бағалауда мәні өте зор. Мектеп математикасында бұл теңсіздіктерді, әр түрлі теңсіздікті дәлелдеуге қолданады. Тақырыпта көрсетілгендей біз теңсіздіктерді теңдеулерді шешу үшін де қолданамыз. Бұл қолданулардың жалпы идеясы мынандай. Қарастырып отырған әр теңсіздіктің теңдікке айналу жағдайлары бар. Осы себепті берілген теңдеуді шешу үшін осы теңсіздіктердің біреуінің теңдік жағдайына келтіреміз. Ол үшін теңдеуді түрлендіріп, теңсіздікке сәйкес белгілеулер енгіземіз. Содан кейін теңдік жағдай орындалатын шартын пайдаланамыз. Ол берілген теңдеуге қарағанда қарапайым теңдеуді береді. Соңғы теңдеудің шешімдері берілген теңдеудің шешімі болады. Осы қарапайым теңдеуді шешіп, берілген теңдеудің шешімін аламыз. Сонымен біздің мақсатымыз: «Жоғарғы математикада қарастырылатын белгілі теңсіздіктерді мектеп математикасындағы кейбір теңдеулерді шешу үшін қолдануға болатынын көрсету» [1] .
Теңдеулерді зерттеу, жуық есептеу, иррационал сандар теориясы, сан қатарлары т. б. теңсіздіктер қасиетіне сүйенеді. Жоғарғы мектептегі математикалық анализ курсында функциялардың максимум және минимум яғни экстримал есептерді шешуде теңсіздіктер кең түрде қолданылады.
Тек математикада ғана емес әр түрлі жаратылыстану ғылымдарында зерттелетін табиғаттың үздіксіз процестері әсіресе экологиялық, экономикалық т. б. халық шаруашылығындағы байланыстар теңсіздіктің көмегімен шешіледі. Теңсіздіктер оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Әр түрлі теңсіздіктер ерте заманда-ақ белгілі болған. Евклид пен Архимед шығармаларында көптеген теңсіздіктер келтірілген. Осы күнгі теңсіздіктер таңбасы ХVІІІ ғасырда ағылшын ғалымы Томас Гариаттың латын тілінде жазылған «Аналитикалық өнердің практикасы атты еңбегінде» тұнғыш рет келтіріледі. Теңдіктер теңсіздіктен жасалады, оларды теңсіздіктердің дербес бір түрі деуге болады. Теңсіздікті теңдікке айналдыру үшін екі шаманың айырмасын дәл бағалау керек. Жалпылама туралы сұрақ қолданбалы сипаттағы сұрақтар қажетті: статистикада, экономикада, ықтималдықтар теориясында, жуықтап есептеу теориясында, физика және т. б. мысалы, қандай да бір шамаға n тәжірибе өткізілді делік. Тәжірибе шарты мүмкіндігінше өзгеріссіз қалды. Осыған қарамастан, жалпы алғанда а 1 , а 2 , …, а n. (1) әр түрлі n сандар алынды. Бұл сандардың арасынан үлкен және кіші шамалар болады. Әдетте санның ақиқат мәні ретінде біз алынған сандардың ішінен ең үлкендері ішінен үлкенің емес және ең кішілерінің ішінен ең кішісін аламыз.
Егер min(a) (1) сандарының ішіндегі ең кішісі болса, ал max(a) олардың ішіндегі ең үлкені болса, онда М ортасы [min(a) ; max(a) ] сегменттің ішіндегі сан болады.
Теңсіздіктер жай санды теңсіздіктер, алгебралық теңсіздіктер, классикалық теңсіздіктер болып бөлінеді. Теңсіздікті дәлелдегенде және шешкенде тек әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алу керек.
Теңсіздікті анықтама арқылы дәлелдеу.
Мысал .
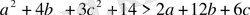 теңсіздігін дәлелдейік.
теңсіздігін дәлелдейік.
Дәлелдеуі.
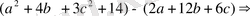

Соңғы кезде
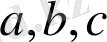 сандарының кез-келген мәнінде оң болады. Теңсіздік дәлелденді.
сандарының кез-келген мәнінде оң болады. Теңсіздік дәлелденді.
Теңсіздіктерді дәлелдеу синтетикалық әдісі.
Мысал .
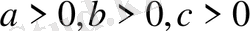 болса, келесі теңсіздікті дәлелдеу керек:
болса, келесі теңсіздікті дәлелдеу керек:
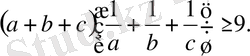
Шешуі: Тірек ретінде келесі теңсіздіктерді алалық:
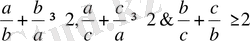
Үш теңсіздікті қосайық:
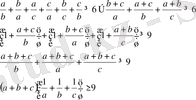
Кері жору әдісімен дәлелдеу
Мысал. Кез келген а саны үшін теңсіздік орындалатындығын көрсетейік
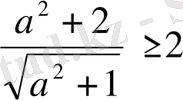 .
.
Дәлелдеу: Кері жорып, қандайда бір а саны үшін қарастырылып жатқан теңсіздік дұрыс емес, яғни теңсіздіктің түрі келесі түрде болады:
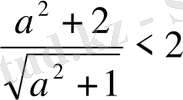 . Бесінші қасиет бойынша теңсіздіктің екі жағында
. Бесінші қасиет бойынша теңсіздіктің екі жағында
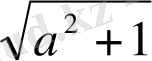 оң санына көбейтеміз, бұдан теңсіздік таңбасы өзгермейді:
оң санына көбейтеміз, бұдан теңсіздік таңбасы өзгермейді:
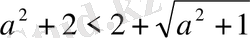 .
.
Екінші қасиет бойынша теңсіздіктің екі жағынан да
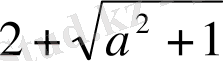 . Оң жағын түрлендіргеннен кейін келесіні аламыз:
. Оң жағын түрлендіргеннен кейін келесіні аламыз:
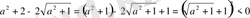 ,
,
яғни
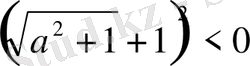 .
.
Соңғы теңсіздік а- ның кез-келген мәнінде орындалмайды, теңсіздіктің оң жағы теріс мәнге ие болмайды, алынған қарама-қайшылық берілген теңсіздіктің дұрыстығын дәлелдейді.
Математикалық индукция әдісімен теңсіздіктерді дәлелдеу
Мысал .
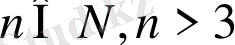 болса, келесі теңсіздіктің туралығын көрсету керек:
болса, келесі теңсіздіктің туралығын көрсету керек:
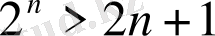 .
.
Дәлелдеуі:
Математикалық қадам:
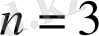 болғанда, теңсіздік тура:
болғанда, теңсіздік тура:
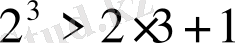
Математикалық болжау:
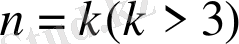 болғанда, теңсіздікті тура деп, яғни
болғанда, теңсіздікті тура деп, яғни
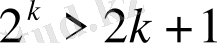 теңсіздігі дұрыс делік.
теңсіздігі дұрыс делік.
Математикалық негіз:
 болғандағы, теңсіздік туралығын, яғни
болғандағы, теңсіздік туралығын, яғни
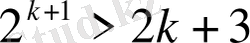 екенін дәлелдеп көрсетейік.
екенін дәлелдеп көрсетейік.
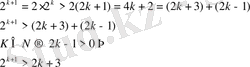
Теңсіздіктерді геометриялық әдіспен дәлелдеу
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz