Математиканың бастапқы курсының теориялық негіздері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 49 бет
Таңдаулыға:

Дәрістер:

Дәріс 1 Математиканың бастапқы курсының теориялық негіздері оқу пәні ғылым ретінде

Білім негізі бастауыш сыныптарда қаланады десек, бастауыш буындарда сабақ беретін мұғалімдердің теориялық даярлығы да жан-жақты, әрі жоғары денгейде болуы тиіс. Осы мақсатта « Математиканың бастапқы курсының теориялық негіздері » пәнін оқып үйрену кезінде болашақ маман мектеп оқушыларына математиканы оқытуға қажетті математикалық біліммен қарулануы тиіс. Бұл үшін олар «жиын», «қатыстар», «сан жіәне шама», «есеп және оларды шешу жолдары» тәрізді негізгі математикалық ұғымдарды меңгерулері және алған теориялық білімдерін бастауыш буын математикасының мазмұнын талдауға қолдана білулері керек. Бастауыш курс негіздерін білу болашақ ұстаздарды тәжірибелік қызметке даярлаумен бірге, математикалық білімдерін әрі кеңейте түсуге негіз болады.

Метематиканың бастауыш курсының өзекті мәселесі теріс емес бүтін сандар, олармен жүргізілетін амалдар, шамалар және оларды өлшеу боолып табылады. Осы өзектің төңірегінде алгебра мен геометрия элементтері шоғырландырылады. Осыған байланысты курста теріс емес бүтін сандар мен оларға қолданылатын амалдарды, осы амалдардың қасиеттері мен заңдарын оқытып үйрету басты орын алады.

« Математиканың бастапқы курсының теориялық негіздері » пәнін оқып-үйрену «математикалық ұғымдар» тарауынан басталады. Математикалық ұғымдардың анықтамаларын берудің жалпы тәсілдерін қарастыруға байланысты мәселелердің осы тарауға енгізілуі-болашақ мұғалімдерде анықтамаларды тұжырымдауды, оларадың құрылысын түсіну мен талдай білуді үйрету қажеттілігінен туындап отыр. Ұғымдардың мазмұны мен көлемі, анықтамаға қойылатын талаптар жайындағы білім мұғалімнің оқушыларға математикалық түсініктер мен ұғымдар қалыптастыру жұмысын дұрыс жүргізе білуін қамтамасыз етеді.

Мұндағы жиындар теориясы мен математикалық логика элементтері мектеп математика курсының негізін құрайтындықтан бұл материал барынша терең, жан-жақты баяндалады. Бұл оқу құралында бастауыш мектептің математика курсында қарастырылатын алгебралық ұғымдардың әр түрлі тұрғыдағы түсініктемелерді келтіреді. Бұл өз кезегінде болашақ бастауыш сынып мұғалімдерінің математикадан теориялық дайындығын арттыра түсуге ықпал жасайды.

Дәріс 2 Математиканың жалпы ұғымдары. Математикалық ұғымдар. Математикалық сөйлемдер

Жоспары:

Математиканың жалпы ұғымдары.
Ұғымның мазмұны мен көлемі
Ұғымның анықтамасы
Ұғымның анықтамасына қойылатын талаптар
Математикалық ұғымдар.

6. Математикалық сөйлемдер . Жай және құрама сөйлемдер

Математика ғылымы, басқа ғылымдар сияқты бізді қоршаған дүниені, табиғи және қоғамдық құбылыстарды, олардың ерекше қасиеттерін зерттейді. Мысалы, геометрия курсында заттардың басқа қасиеттеріне көңіл аудармай (түсі, массасы, қаттылығы, т. б. ) олардың формалары мен өлшемдерін қарастырамыз. Сондықтан геометрияда «зат» деген сөздің орнына «геометриялық фигура» деген сөз қолданылады. Сәуле. түзу, бұрыш, дөңгелек, шаршы - бұлардың барлығы геометриялық фигуралар. Олар жалпылама ұғымдар да абстракциялау ( жалпылау) нәтижесі болып табылады. Жалпы, кез келген математикалық обьектілер - бізді қоршаған дүниедегі заттар мен құбылыстардың басқа қасиеттерінің ішінен сандық және кеңістік қасиеттерін бөліп алу нәтижесі. Ендеше, математикалық оьектілер геометриялық фигуралар, сандар, т. б. шындық дүниеде жоқ. Олардың барлығы қоғамның даму тарихы барысында пайда болып, адамның тек қиялында өмір сүреді.

Бұған қоса математикалық ұғымдардың жасалуында сәйкес заттардың көптеген қасиеттерін жалпылаумен қатар, іс жүзінде ешбір затта жоқ қасиеттерді де меншіктеу болады. Мысалы, түзу деп аталатын математикалық обьектіде нақты заттардың ұзыннан -ұзақ созылу қасиетімен бірге оның өмірде кездесетін заттардың арасында бірде - біреуі ие болмайтын екі жаққа да шексіз созылу қасиеті бар.

Ұғымның мазмұны мен көлемі

Кез келген математикалық оьектінің өзіне тән белгілі бір қасиеттері болады. Мысалы, шаршының төрт қабырғасы өзара тең, барлық бұрыштарды тік және диагональдарды өзара тең. Шаршының бұдан басқа да қасиеттерін көрсетуге болады. Обьектіні басқа обьектіден айыра білу үшін оның қасиеттерін негізгі және негізгі емес қасиеттер деп бөлуге болады. Белгілі бір обьектіге ғана тән және ол қасиетсіз сол обьектіні анықтау (танып-білу) мүмкін болмайтын қасиеттер жатады. Шаршының жоғарыда аталған қасиеттері - негізгі қасиеттер, ал «АВСD шаршысының АD қабырғасы горизанталь” - деген қасиетті негізгі емес. Өйткені шаршы басқаша да орналасуы мүмкін ғой.

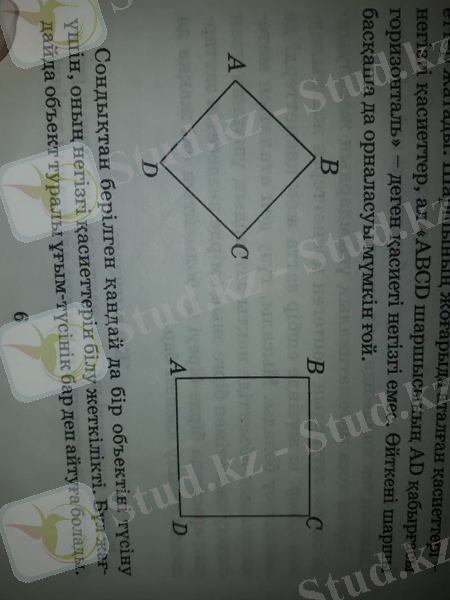
$C:\Users\Раушан\Downloads\WhatsApp Image 2019-10-23 at 08.30.56.jpeg$

Сондықтан берілген қандай да бір обьектіні түсіну үшін, оның негізгі қасиеттерін білу жеткілікті. Бұл жағдайда обьект туралы ұғым - түсінік бр деп айтуға болады.

Обьектінің өзара байланысты барлық негізгі қасиеттерінің жиынтығын осы обьект туралы ұғымның мазмұны деп атайды.

Математикалық обьект туралы айтқанда бір ғана сөзбен, терминмен түсіндірілетін барлық обьектілердің жиынтығы айтылады. Мысалы, үшбұрыш туралы айтқанда, үшбұрыш болып есептелетін барлық геометриялық фигуралар туралы айтылады. Барлық үшбұрыштың жиынтығы үшбұрыш туралы ұғымды құрайды.

Жалпы ұғымның көлемі дегеніміз - бір ғана сөзбен, терминмен белгіленетін барлық обьектілердің жиынтығы.

Сонымен, кез келген ұғым аталу терминімен, көлемімен және мазмұнымен сипатталады екен.

Ұғымның мазмұны мен көлемінің арасында мынадай байланыс бар:

Ұғымның көлемі неғұрлым «артық» болса, оның мазмұны соғұрлым « аз» болады. Мысалы, «тәк бұршты үшбұрыш» ұғымның көлемі «үшбұрыш» ұғымының көлемімен «кіші», өйткені, алғашқы көлеміне барлық үшбұрыштар ғана кіреді. Бірақ «тік бұрышты үшбұрыш» ұғымының мазмұны « үшбұрыш» ұғымының мазмұнынан «артық». яғни кеңірек. Өйткені тік бұрышты үшбұрыш баарлық үшбұрыштарға қасиеттермен қоса, өзіне ғана тән қосымша қасиеттерге математикалық түрде математикалық ұғымдарға өте бай. 1-сыныптың өзінде оқушылар «цифр», «сан», «қосылғыш», «қосындының мәні», «кесінді», т. б. ұғымдармен танысды. Сынып жоғарылаған сайын мұндай ұғымдардың саны артып, кеңнйе береді. Ендеше, болашақ бастауыш сынып мұғалімі ұғым туралы жоғарыда баяндалған мәселелерді білуге міндетті.

Ұғымның анықтамасы

Қандай бір математикалық объект ұғымының мазмұны осы объектінің көптеген негізгі қасиетерін қамтиды. Дегенмен, объект берілген ұғымның көмегінде болатындығын тағайындау үшін, (яғни объектіні танып - білу үшін) оның кейбір негізгі қасиеттерінің бар-жоғын тексеру қажет. Объектіні танып-білу үшін жеткілікті болатын объектінің негізгі қасиеттері осы объект туралы ұғымның анықтамасы деп аталады.

Жалпы, анықтама дегеніміз - ұғымның мазмұнын ашатын логикалық операция. Ұғымды анықтау жолдары әр түрлі. Алдымен оларды айқын және айқын емес деп бөлуге болады. Айқын анықтамалар екі ұғымның дәлме-дәл келетін теңдігі формасына болады. Мысалы, тікбұрышты үшбұрыш бұл- бір бұрышы тік болатын үшбұрыш. Осы анықтамадағы «тік бұрышты үшбұрыш» деген ұғымды а арқылы белгілесек, ал, «бір бұрышты тік» деген ұғымды в арқылы белгілесек, онда тік бұрышты үшбұрыш туралы анықтама мынадай түрде болады: « а бұл в».

Айқын емес анықтамаларда екі ұғымның дәлме-дәл келу формасы болады. Мұндай анықтамалардың мысалы ретінде контекстуалды және остенсивті анықтамаларды айтуға болады.

Контекстуалды анықтамаларда жаңа ұғымның мазмұны мәтіннің үзіндісі арқылы ашылады, яғни нақты жағдайда енгізілетін ұғымның мағынасын сипаттайтын контекст арқылы ашылады.

Айқын анықтамаларда екі ұғым теңестіріледі. Олардың бәрін анықталушы, екіншісін анықтаушы ұғым деп айтады. Анықтаушы ұғым арқылы, анықталушы ұғымның мазмұны ашылады. Мысал ретінде шаршы анықтамасының құрылымын талдайық :« Шаршы деп барлық қабырғалары тең болатын тік төртбұрышты айтамыз». мұнда алдымен, анықталушы ұғым - оның қасиеттері көрсетілген: «Барлық қабырғалары тең болатын тік төртбұрыш» болуы .

«Тіктөртбұрышты болу» қасиеті барлық швашылар тіктөртбұрыш болатындығын, яғни «тіктөртбұрыш» туралы ұғым « шаршы» ұғымына қарағанда жалпылама болып есептеледі. Ол анықтаушы ұғым «Шаршыға» қатысты алғанда негізгі болып есептеледі.

Екінші қасиет - «барлық қабырғаларының тең» болуы - ол шаршыны басқа тік төртбұрыштардан айыру үшін көрсетілген сыртқы қасиет.

Мектеп курсы математикасындағы басқа анықтамаалрыдың құрылымы да тұра осындай. Мұндай анықтамалардың құрылымын схема түрінде былацйкөрсетуге болады:

Бастауыш курс математикасында мұндай түрдегі анықтамалар беріләтін ұғымдар саны көп емес. Мұндай анықтаманың көмегімен, мысалы, көбейту амалы анықталады: « Бірдей қосылғыштардың қосындысын көбейту деп айтамыз». Бастауыш сыныптарда көпшілік жағдайда ұғымды анықтауда остенсивті және контекстуалды анықтамалар қолданылады. Кейбір жағдайларда контексті де және көрсетуді де қамтитын анықтамаларда да кездескеді. Мұндай анықтаманың мысаылы ретінде тіктөртбұрыштың анықтамасын айтуға болады (2-сынып) . Мұнда тік төртбұрыштардың суреттері көрсетіледі де, мынадай мәтін беріледі: «Бұл төртбұрыштардың барлық бұрыштары тік». Ал тік төртбұрыштардың астында «Бұлар -тіктөртбұрыштар» деген жазу келтірген.

Ұғымның анықтамасына қойылатын талаптар

Айқын анықтамалардың дұрыстығына баға беру үшін ұғымды анықтау ережелерін білген дұрыс.

Бастауыш курс математикасындағы анықтамалардың көпшілігі тегі және түрлік айырмашылығы бойынша беріледі. Бұл тәсілмен ұғымды анықтау кезінде мынадай бірнеше талаптарды сақтау керек:

1. Анықталушы және анықтаушы ұғымдар бір-бірімен өлшемдес болуы керек. Мысалы ретінде «тіктөртбұрыш» пен «төртбұрыштың» анықтамаларын алуға болады.

2. Анықтама беру ережелері тұйыққа тірелуге тиым салуы керек, яғни ұғымды оның өзі арқылы немесе өз кезегінде сол арқылы анықталатын басқа бір ұғыммен анықтауға. Мысалы,

көбейтіндіні көбейту амалы арқылы.

3. Анықтамада ұғымның көлеміне тиісті обьектіні - бір мәнді ерекшелеуге мүмкіндік беретін барлық қасиеттерді көрсетілуі тиіс. Мысалы, сыбайлас бұрыштардың анықтамасы былай деп беріледі: «Сыбайлас бұрыштар деп - қосындысы 180 ${^\circ}$ болатын бұрыштарды айтады». Бұл анықтама сыбайлас бұрыштарды басқа бұрыштардан айыра білуге жеткіліксіз.

4. Анықтамада басы артық ештеңе болмауы тиіс, яғни көпсөзділік болмауы керек. Мысалы, тіктөртбұрыштың анықтамасында басы артық сөздер кездеседі.

5. Кейбір ұғымдардың мүмкін болатын анықтамаларының бірін таңдау кезінде қайсы анықтама жеңіл, табиғи немесе әрі қарай теорияны құру мақсатына сәйкес болатындығы басшылыққа алынуы керек. Мысал ретінде параллелограмның анықтамаларын салысыстыруға болады.
6. Анықталушы ұғым өмірде бар болуы қажет. Сонда ғана анықтама логикалық тұрғыдан алғанда дұрыс болады. Мысалы: «Доғал бұрышты үшбұрыш деп - барлық бұрыштары доғал үшбұрышты айтады». Бұл анықтама жоғарыда аталған талапқа сай емес. Өйткені барлық бұрыштары доғал болатын үшбұрыш жоқ.

Математикалық сөйлемдер. Жай және құрама сөйлемдер

Адам баласы өзін қоршаған дүниені танып, білген сайын математикалық обьектілер арасындағы, объектілер мен олардың қасиеттері арасындағы түрлі байланыстарды тағайындайды. Тілде бұл байланыстар сөйлемдер арқылы өрнектеледі. Ендеше, тілдегі сияқты математикада да сөйлемдер болады. Кез келген математикалық сөйлем оның мазмұны және логикалық құрылымымен сипатталады. Біз негізінен сөйлемдердің логикалық құрылымына көңіл аударамыз. Математикалық сөйлемдерді логикалық құрылымына қарай жай және құрама сөйлемдер деп екіге бөлеміз.

Берілген дене немесе объект туралы бір ғана ойды білдіретін сөйлемдерді жай сөйлемдер деп атаймыз.

Мысалы: 25 саны тақ сан. Бұл - жай сөйлем, өйткені сөйлемде объект ретінде алынып тұрган 25 санының тек тақ сан екендігі туралы ғана айтылып тұр.

Екі немесе бірнеше жай сөйлемдерден құралған сөйлемдерді құрама сөйлемдер деп атаймыз. Басқаша, берілген дене немесе объект туралы екі немесе бірнеше ойды білдіретін сөйлемдерді құрама сөйлемдер деп атаймыз. Мысалы, 25 саны тақ сан және 5-ке бөлінеді. Бұл құрама сөйлем. Өйткені, бұл сөйлем «25 саны тақ сан» және «25 саны 5-ке бөлінеді» деген екі жай сөйлемнен құралаған. Басқаша айтқанда, бұл сөйлемде берілген дене немесе объект 25 саны туралы екі ой айтылып тұр. Оның біреуі - 25 санының тақ сан екендігі, екінші - 25 санының 5-ке бөлінетіндігі.

Құрама сөйлемдерді алу үшін «және», «немесе», «егер . . . онда», «емес», т. б. сөздерді пайдаланамыз. Оларды математикада логикалық байламдар деп атайды. Аталған логикалық байламдарға байланысты құрама сөйлемдердің логикалық құрылымы анықталады. Құрама сөйлемдердің логикалыө құрылымын анықтау үшін, мыналарды тағайындау керек:

1. Құрама сөйлемдердің қандай жай сөйлемдерден жасалғанын.

2. Қандай логикалық байлам арқылы жасалғанын.

Енді құрама сөйлемдердің логикалық құрылымын анықтауды мысалдар арқылы көрсетейік.

1. 25 саны тек сан және 5-ке бөлінеді. Бөйлем екі жай сөйлемнен құрлған. Бірінші жай сөйлем А-деп, ал екіншіжай сөйлемді В-деп белгілесек, онда А және В түріндегі (формасындағы) Сөйлемді аламыз. Оны қысқаша быдай жазуға болады: А ˄ В, ˄- белгісі - конъюнкция белгісі қазақша «біріктіремін» деген мағына береді. Оқылуы: «А және В».

2. «6саны 8-ден үлкен немесе 8-ге тең». «6саны 8-ден үлкен»деген жай сөйлемді А-деп, ал «8-ге тең» деген жай сөйлемді В-деп белгідеп, А немесе В формасындағы сөйлемді аламыз. Оны қысқаша былай жазады: А ˅ В, ˅-белгісі - дизъюнкция белгісі. Қазақша «ажыратамын» деген мағына береді. Оқылуы: «А немесе В».

3. «Егер үшбұрыштың табанындығы бұрыштары тең болса, онда үшбұрыш тең бүйірлі». «Үшбұрыштың табанындағы бұрыштары тең». Оны А-деп, ал «үшбұрыш тең бүйірлі» деген жай сөйлемді В-деп белгілесек, онда егер А, онда В формасындағы сөйлем аламыз. Оны қысқаша былай жазуға болады:А→ В. → - белгісі импликация белгісі. Қазақша «шығады» деген мағына береді. Сонда А→ В формасындағы сөйлемді басқаша «А сөйлемінен В сөйлемі шығады»деп те оқуға болады. Оқылуы: «Егер А, онда В»

4. «Емес» деген логикалық байлам арқылы жасалатын сөйлемнің құрылымын анықтау үшін, «15 саны тақ сан» деген сөйлем алайық та, оны А-деп белгілейік. Енді осы сөйлемнің соңына «емес» деген логикалық байламды тіркеп жазайық. Сонда: «15саны тақ сан емес деген жаңа сөйлемаламыз. Соңғы сөйлемнің формасы А емес болып шығады. Оны қысқаша былай жазамыз - А. Оқылуы: «А емес». А-ның алдындағы сызықша белгісі «терістеу»деп аталады. Ендеше. біз «15 саны тақ сан» деген сөйлемді «15 саны тақ сан емес» деп теріске шығарып отырмыз.

Бастауыш сынып математикасында матеаматикалық сөйлемдер туралы айқын түсінік берілмейді. Алайда өрнектерді, теңдіктерді оқу кезінде біз іс - жүзінде математикалық сөйлемдермен кездесеміз. Сондықтан болашақ бастауыш сынып мұғалімінің математикалық сөйлеидер туралы түсінігі болғаны дұрыс.

Дәріс 3 Жиындар және оларға қолданылатын амалдар

Жоспар:

Жиын ұғымы. Жиын элементi. Жиыннын берілу тәсілдері
Тең жиындар. Бос жиын. Ішкі жиын, оның түрлері. Универсал әмбебап жиын.

Жиын ұғымы. Жиын элементi. Жиыннын берілу тәсілдері

Жиын ұғымы- математикада аныкталмайтын негізгі ұғымдардын бірі, яғни жиынға белгілі бір түрдегі анықтама берілмейді. Сондыктан оны тек мысалдармен гана туcіндіруге болады. Мысалы, сандар жиыны, геометриялық фигуралар жиыны, оқушылар жиыны, ағаштар жиыны, оқушы құралдарының жиыны, т. б.

Сонымен, «жиын» сезін «жиналыс», «жиынтык», «топ» сиякты мағыналас сөздермен алмастыруга болады. «Жиын» сезі карапайым тілде заттардыц тобы түрінде ұғым береді. Математикада жиын угымы баска- ша тусіндіріледі. Мүнда заттардыц саны көп болуы MIндетті емес. Бір ғана заттын өзі жиын бола алады.

Жиындарды шартты түрде белгілеу үшін латынның А. В. С., D . . . Z сиякты бас әpіптері қолданылады. Жиынға тиісті әрбір затты жиын элементi деп атайды. Жиын элементтерін латынның кіші әріптерімен белгілейді: а, b, с. d, . .

Математикада және ғылымның басқа да салаларында қандай бір объектінің қарастырылып отырылған жиынға тиісті немесе тиісті емес екендігін анықтауға тура келетін жағдайлар жиі кездеседі. Мысалы, 7 саны натурал сан. Басқаша айтканда 7 саны натурал сандар жиынына тиісті деп айтуға болады. Жалпы, «а объектісі А жиынына тиісті»-деген сөйлемді арнайы белгінін көмегiмен былай жазуға болады: а є А. Бұл сөйлемді турліше окиды:

а объектіcі А жиынына тиісті.

- а объектіci A жиынының элементі.

- А жиынында а элементі бар.

А жиыны а элементін қамтиды. «а объектісі А жиынына тиісті емес» деген сөйлемді а€А түрінде жазамыз. Бұл сөйлем былай оқылады:

- а объектісі А жиынына тиісті емес.

а объектіcі А жиынының элементі емес.

- А жиынына а элементі жатпайды.

Жиынды және оның элементін былай жазу келісілген. Мысалы, А - жиыны белгіcінен кейін тендік белгісін қойып, фигуралы жақшаның ішіне жиын элементтерін жазамыз: А-{а, b, с, d}.

Жиын элементі жиынға бір рет қана тиісті болады.

Жиын элементтерінің саны шектеулі және шектеусіз болады. Мысалы, ай күндерінің саны, сыныптары окушылар саны, т. б. шектеулі, ал түзудін бойындағы нүктелер саны шектеуcіз. Сондай-ак сан жиындары - натурал, бүтін, рационал, накты сандар жиындарының элементтерінің саны өте көп, шектeycіз. Бұл жиындарды мынадай әpіптермен белгілейміз:

N - натурал сандар жиыны;

Z - бутін сандар жиыны;

Q - рационал сандар жиыны;

R - нақты сандар жиыны.

Жиынды схема түрінде белгілеу үшін, тұйықталған контурды пайдаланамыз. Оны Эйлер-Венн диаграммасы деп атайды.

Леонард Эйлер (1703-1783) Петербург Ғылым академиясьның мүшеcі, Швейцарияда туған, ал 1727 жылы Петербург Fылым академиясының шақыруымен Ресейге келген және мүнда ірі математик дәрежесіне дейін көтерілген. Джон-Венн (1834-1923) ағылшын математигі.

Жиын ұғымын біз анықтамасыз қолданатынымыз туралы айтқан болатынбыз. Қандай да бір заттар тобы жиын бола ала ма, жок па, оны қалай білуге болады?

Егер әрбір объект туралы, оның жиынға тиісті немесе тиісті емес екендігі туралы айта алатын болсак, онда жиын берілген деп есептеледі (саналады), яғни жиын өзінің элементтері арқылы анықталады. Жиыннын беpілуінің мынадай негізгі екі тәсілі бар:

1. Жиынды оның барлык элементтерін ту арқылы беру. Мысалы, А жиыны 1-ден 6-га дейінгі сандар болсын. Бұл жағдайда жиынды былай жазып көрсетуге болады: A=(1, 2, 3, 4, 5, 6 )

Кейбір жағдайда жиын элементтері шектеусіз (шексіз) көп болуы мүмкін. Мұндай жағдайда жиын элементтерінің барлығын жазып көрсету аркылы беру мүмкін емес. Бұл жағдайда жиын элементтерінін характеристикалык (сипаттамалык) касиеттерін көрсету арқылы беруге болады.

Сонымен жиынның берілуінің 2-ші тасілі:

2. Жиынға тиісті элементтердің бәріне ортақ сипаттамалық қасиеттерін көрсету аркылы беру. Мысалы, В 6-дан артық барлык натурал сандар жиыны болсын. Бұл жиынның барлық элементтерін жазып көрсету мүмкін емес. Сондықтан бұл жиынды мынадай турде жазып көрсетуге болады:

В- {x/x € N, x>6}

Жиындарды берудін 2-ші тәсілі жалпылама түрде алынған. Бұл тәсіл арқылы элементтері шектеулі және шектеусіз жиындарды беруге болады.

Бастауыш курс математикасында жиын ұғымы және жиын элементтері айқын түрде берілмейді. Дегенмен, олар бастауыш курс математикасының өн бойында қолданылады

Тең жиындар. Бос жиын. Ішкі жиын, оның түрлері. Универсал әмбебап жиын.

Анықтама: Егер А және В жиындары бірдей элементтерден тұратын болса, онда мұндай жиындарды тең жиындар деп атайды және былай белгілейді: А=В

Мысал: А={2, 4, 6, 8}, В={6, 4, 2, 8}. Көріп отырғанымыздай, А және В жиындары бірдей элементтерден тұрады. Ендеше А=В.

Ескерту: Жиындардың теңдігін анықтағанда элементтердің орналасу реті есепке алынбайды.

Анықтама: Бірде - бір элементі жоқ жиынды бос жиын деп атайды және оны былай белгілейді: Ø.

Ескерту: Бос жиынның белгісі фигуралы жақшаға алынбайды. Мысалы, А= Ø түрінде жазылады.

Мысал: А= {11, 12, 13, 14, 15} жиыны берілсін. Осы жиын элементтерін ішінен бір таңбалы сандарды теріп жазу керек болсын. Ол жиынды В деп белгілесек, онда В жиынына тиісті болатын элементтер жоқ. Ендеше, В= Ø.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.