Қолданбалы есептерді шешу туралы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

12. Қолданбалы есептерді шешу туралы

Ереже тоғызыншы. Қолданбалы есептерді математикалық әдістермен шешуге үйрету математикалық курстардың міндеті емес, мамандық бойынша курстардың міндеті болып табылады.

Бұл ереже жоғары техникалық оқу орындарындағы математикалық курстар да, олар үшін математика оқулықтары да жиі сыналатын мәселелердің біріне қатысты. Әрине, нақты құбылыстарды зерттеу үшін математикалық ұғымдарды қолдануды суреттейтін қарапайым нақты мысалдар: материалдық нүктенің қозғалысының туынды жылдамдығы немесе өзектің сызықтық тығыздығы, Интеграл-күш жұмысы, дифференциалдық теңдеулерді құрастыру - Радиоактивті ыдырау теңдеуін шығару және т. б. туралы түсінік өте пайдалы. Сонымен қатар, тоғызыншы позицияны математиктердің қолданбалы есептерді шешуге студенттерді оқытудың орынсыз екендігі туралы ұсыныс ретінде түсіну қате болар еді. Бұл әрдайым жасалды және жасалады, өйткені ол қажет және пайдалы.

Бұл мәселе емес, студенттерді математика курсында оқып жатқан математикалық әдістерді қолданбалы есептерді шешуге жүйелі түрде оқыту міндетті түрде жоғары техникалық немесе басқа арнайы (математикалық емес) оқу орнының бейінді кафедраларында жүзеге асырылуы керек. Бұл осы кафедралардың мызғымас міндеті болуы тиіс. Тек осы жағдайда студент өзінің кәсібінде математикалық әдістерді білу мен қолдану қажеттілігі мен қажеттілігіне сенімді бола алады.

Егер бейінді кафедраларда бұл жасалмаса, онда бұл мамандық үшін осы институтта оқытылатын көлемде математика қажет емес екендігінің белгісі немесе, мүмкін, ондағы арнайы пәндерді оқудың дисфункционалды қойылымының белгісі болуы мүмкін. Қалай болғанда да, институттағы барлық оқу процесінде арнайы пәндерді ұсынуда кеңінен қолданылатын жағдайда математиканы үйренудің айтарлықтай үлкен пайдасы болады. Бұл, өкінішке орай, әрдайым емес.

Математикалық курстарға нақты құбылыстарды сипаттайтын дифференциалдық теңдеулер жеткіліксіз мөлшерде шығарылады деген талаптар жиі қойылады. Сынның бұл түрі көбінесе көптеген адамдарға тән мінез-құлықпен байланысты, олар өздері не істеу керек екенін жасамай, басқалар мұны істеу керек деп сенімді түрде айтады және оларды жаман істегені үшін сынайды. Менің ойымша, бұл мәселеде нақты құбылыстарды математикалық модельдеу, яғни мұндай құбылыстың математикалық моделін құру математиканың міндеті емес екенін нақты айту керек. o

Математиканың міндеті, жоғарыда айтылғандай, математикалық модельді, оның қасиеттері мен ерекшеліктерін зерттеу болып табылады. Математикалық курстарда барлық математикалық модельдер құрылмайтындығы, осы мамандық үшін қажетті барлық дифференциалдық теңдеулер шығарылмайтындығы таңқаларлық емес, бірақ бұл арнайы курстарда жасалмайды. Мәселен, мысалы, кез-келген құбылысты сипаттау үшін Лаплас теңдеуі немесе жылу өткізгіштік теңдеуі көрсетілетін жалпы физикалық курсты табу қиын (әрине, бұл теориялық физика емес) . Бұл курстардан оларда қарастырылған теңдеулердің әртүрлі шекаралық шарттарын талдауды табу одан да қиын (математиктер мұның бәрін жасауы керек деп болжанады, дегенмен, егер олар қаласа да, оларды математикалық курстарға бөлінген уақыт аясында жасау мүмкіндігінен айырылады) .

Математика курсын оқығаннан кейін студенттер қандай да бір теңдеуде қандай да бір мүшенің әдетте қажетті физикалық мағынасын білмейтіндіктен, мұнда қарастырылған математикалық курстарға қатысты қорлауды да қамтуы керек. Маған математиканың жалпы курсына мұндай қорлау әділетсіз болып көрінеді. Теңдеу мүшесінің нақты физикалық мағынасын нақтылау бұл сонымен қатар арнайы пәндердің мәселесі және оны математиктердің иығына салмаңыз (біз болашақ студенттің мамандығына байланысты нақты мақсатқа бағытталған арнайы курстар туралы емес, математиканың жалпы курсы туралы айтып отырмыз) . Математика математикалық модельдерді зерттейтіндіктен, теңдеулерді зерттеудегі оның міндеті келесі сұрақтар болуы мүмкін, мысалы: теңдеудің осы мүшесінің өзгеруі шешімнің болуына, оның бірегейлігіне, асимптотикалық мінез-құлқына, мәселенің дұрыс қойылуына, шешімнің тұрақтылығына және т. б. қалай әсер етеді.

Студенттермен оқушыларды қолданбалы есептер шешу бағдарламаларын құруға үйрету жолдарының бірі қолданбалы есептер шешу. Қолданбалы есептерді кезеңдерге бөліп әрбір кезеңнің өз есебіне алгоритмдер және бағдарламалар құру. Құрылған бағдарламаларды біріктіріп берілген бас есепті шешу әдістерін үйрету. Алынған нәтижелердің дұрыстығын талдау.

Біз төменде бас есепті жеке кезеңдерге бөліп әрбір кезең үшін алгоритім және программа құрып құрылған программаларды бас есепті шешуге пайдалану әдісін қарастырамыз.

Туындыны қолданбалы есептерді шығаруда қолдану

Туындының механикалық мағынасын алғаш рет И. Ньютон берген.

Ол келесідей тұжырымдалады:

у = f(x) функциясының х нүктесіндегі f´(x) туындысы оның х нүктесіндегі өзгеру жылдамдығын анықтайды. Бұл туындының механикалық мағынасы.

Екінші туындының механикалық мағынасы

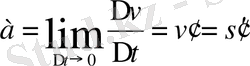
Туындыны қолдану мысалдары

Қуат - жұмыстан уақыт бойынша алынған туынды

N = A ‘ (t)

Басыl= 0 нүктесінде орналасқан ұзындығыlжәне массасы m(l) біртекті емес стержень берілген. Стерженніңlұзындығы бойынша массалық функциясының туындысы стерженнің берілген нүктедегі сызықтық тығыздығы:

ρ(l) = m ‘ ( l )

3) Жылу сиымдылығы - жылудың температура бойынша туындысы:

C(t) = Q ’(t)

4) Тоқ күші - зарядтан уақыт бойынша туынды:

I = q ‘ (t)

Есептер шығару

1. Нүкте келесі заңдылықпен қозғалуда

а) кез келген t ( t > 0) уақыттағы жылдамды есептейтінр формуланы қорытып шығарыңыз;

б) t = 2c мезеттегі жылдамдықты табыңыз;

в) қозғалыс басталғаннан кейін неше минутта нүкте тоқтайды?

Шешуі:

а) v(t) = - t ² + 4 t + 5.

б) v(2) = - 2 ² + 4∙2 + 5 = - 4 + 8 + 5 = 9(м/с) .

в) v(t) = 0, - t ² + 4 t + 5 = 0, t ₁ = -1, t ₂ = 5,

-1 < 0, есеп шартын қанағаттандырмайды.

Қозғалыс басталғаннан кейін 5 минутта нүкте тоқтайды.

2. v ₀ жылдамдықпен жоғары вертикаль жіберілген дененің жылдамдығы заңдылығымен анықталады, мұндағы h -метрмен биіктік, t- секундтағы уақыт.

Егер, g = 10м/с2 болса, дененің ең үлкен биіктігін табыңыз

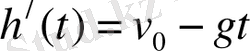Шешуі:

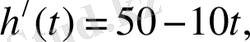
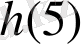=125.

Жауабы: 125 м.

3. Ұзындығы 25 см жұқа біртекті емес стерженде массасы (граммен) келесі заңдылықпен таралады, мұндағы l - стержень басынан кез келген нүктесіне дейінгі қашықтық. Басынан 4 см қашықтықтағы стерженнің тығыздығын табыңыз.

Шешуі:

ρ(l) = m ‘ (l)

ρ(l) = 8l - 2, ρ(4) = 32 - 2 = 30

Жауабы: 30 г\см3

4. Q (t) массасы 1 кг денені 0 ⁰ С-тан t ⁰ -қа (Цельсимен) қыздыратын жылу саны және 0 ⁰ С - тан аралығында

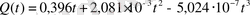
Формуласы дәл мәніне жақсы жуықталады.

Су сиымдылығының t - дан тәуелділігін табыңыз.

Шешуі:

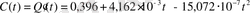
5. Өткізгіштен өтетін жылу келесі формуламен берілген: q(t) = t+4/t.

Уақыттың қандай мезетінде өткізгіштегі тоқ нөлге тең?

Шешуі: I(t) = q ‘ (t),

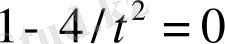
Бұдан, t = 2 немесе t = -2; t = -2 есеп шартын қанағаттандырмайды.

Жауабы: t = 2.

Бас есептің қойылуы . Берілген жазықтықта n - деңгей үшбұрыштары (Х[i, j], Y[i, j], Z[i, j] ) i=1…n, j=1…3 координаталарымен берілген. Мүнда i - индексі ұшбұрыш номерін, j - индексі ұшбұрыш төбелерінің номерін көрсетеді. Осы деңгей үшбұрыш торабында квадрат торабының (xs[i, j], ys[i, j] ), i =1…ns, j = 1…ms, түйін нүктелерінің zs[i, j] деңгей биіктігін табу талап етіледі (1-сурет) . Мүнда i, j - түйін нүктелерінің сәйкес жол және баған индекстері.

Жоғарыда сипаталған бас есепті төмендегі кезеңдерге бөліп шешеміз. Мүнда (xs[i, j], ys[i, j] ) түйін нүктелерінің әрбірін M(xt, yt) берілген нүкте деп аламыз. Осы M(xt, yt) нүкте үшін төмендегі есептеу жүмыстарын орындаймыз. M(xt, yt) координаталы нүктенің қайсы үшбұрышқа тиістілігін анықтаймыз. M(xt, yt) нүкте тиісті үшбұрышта M(xt, yt) нүктенің zt деңгей биіктігін анықтайтын координатасы табылсын.

Бұл берілген бас есепті шешу бағдарламасын құру үшін төмендегі алгоритмдерді құрамыз.

M(xt, yt) нүктенің түзуге қатысты орналасуын анықтайтын алгоритм.
M(xt, yt) нүктенің үшбұрышқа тиістілігін анықтайтын алгоритм.
M(xt, yt) нүктенің берілгенn -үшбұрыштардың қайсысына тиістілігін табу және M(хt, yt) берілген нүктенің деңгей биіктігін табылған деңгей үшбұрышымен аппроксимациялау алгоритмі.

Осы алгоритімдер мен олардың программалары төменде берілген.

Нүктенің түзуге қатысты орналасуын анықтайтын алгоритм.

1есеп. Жазықтықта берілген M(xt, yt) нүктенің A(x ₁ , y ₁ ) және B(x ₂ , y ₂ ) екі нүктеден өтуші түзуге қатысты орналасуы анықталсын.

Шешу алгоритмі:

1-қадам. Берілген нүктенің xt, yt координаталарын енгізу.

Екі нүктеден өтуші түзудің x1 y1; x2 y2 координаталарын енгізу.

2-қадам. Екі нүктеден өтуші берілген түзудің теңдеуіне берілген нүктенің xt, yt координатасын қойып

өрнегін аламыз.

3-қадам. zt1 өрнектің мәні zt1>0 болса нүкте берілген түзуге қатысты жоғарыда орналасқан. Егер zt1<0 болса, берілген M(xt, yt) нүкте түзуге қатысты төмен орналасқан.

Егер zt1=0 болса онда нүкте түзу бойында орналасқан.

1-есеп бағдарламасының тексті.

program ntkoa; uses crt;

var xt, yt, x1, y1, x2, y2:real;

zt1: real;

begin clrscr;

write (‘xt, yt=’) ; read(xt, yt) ;

write (‘x1, y1, x2, y2=’ ) ; read (x1, y1, x2, y2) ;

zt1:= (yt-y1) *(x2-x1) -(xt-x1) *(y2-y1) ;

write (‘zt1=’, zt1:6:2) ;

if zt1>0thenwrite(’нүкте жазықтықтан жоғары орналасқан’) ;

if zt1=0 then write (‘нүкте түзу ойында орналасқан’) ;

if zt1< 0 then write (‘нүкте түзуден төменде орналасқан’) ;

readkey;

end.

Ескерту: Мұнда A(x1, y1), B(x2, y2) нүктелердің абсциссаларының х осьіне сәйкес өсуі бойынша енгіземіз, яғни солдан оңға қарай.

Егер A(x1, y1), B(x2, y2) нүктелердің координаталарын кері бағытта енгізсек zt1 мәні қарама-қарсы таңбаға ауысады.

2. Берілген нүктенің үшбұышқа тиістілігн анықтау алгоритімімен программасы.

2-есеп. Жазықтықта берліген M(xt, yt) нүктенің берілген ∆ABC-ға тиістілігін төбелерінің координаталары A(x1, y1), B(x2, y2), C(x3, y3) болғанда анықтау керек.

Шешу алгоритмі:

1-қадам . Берілген M(xt, yt) нүктенің xt, yt координаталарын және ABC үшбұрышының A(x1, y1), B(x2, y2), C(x3, y3) төбелерінің сәйкес (x1, y1), (x2, y2), (x3, y3) - координаталарын енгізу.

2-қадам . Берілген үшбұрыштың әрбір қабырғасына тиісті төбелерінің (x1, y1, x2, y2), (x2, y2, x3, y3) және (x3, y3, x1, y1) координаталарынан өтуші сәйкес өрнектерді түзу теңдеуінеxt, yt координаталарын қойып аламыз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.