Дифференциалдық теңдеулер: бірінші және екінші ретті теңдеулер, Коши есебі және шешу әдістері (айнымалыларды бөлу, біртектес түрге ауыстыру)


Магистрант ММ-11 тобы: Ибатова А. С.
Дифференциалдық теңдеулер.
Бірінші ретті дифференциалдық теңдеулер
Бірінші ретті дифференциалдық теңдеулер деп тәуелсіз айнымалыны, ізделінетін функцияны және оның бірінші ретті туындысын байланыстыратын теңдеуді айтады, яғни
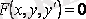 (1)
(1)
Егер (1) теңдеу
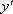 туындысы арқылы шешілетін болса, онда
туындысы арқылы шешілетін болса, онда
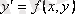 (2) теңдеуі туындысы бойынша шешілген бірінші ретті жай дифференциалдық теңдеу деп аталады.
(2) теңдеуі туындысы бойынша шешілген бірінші ретті жай дифференциалдық теңдеу деп аталады.
Егер кез келген
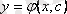 функциясының (2) теңдеудегі
функциясының (2) теңдеудегі
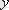 және
және
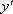 -тің орнына қойғанда ол теңдеу тепе - теңдікке айналса, онда оны (2) теңдеудің шешуі деп атайды.
-тің орнына қойғанда ол теңдеу тепе - теңдікке айналса, онда оны (2) теңдеудің шешуі деп атайды.
(2) теңдеудің
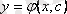 жалпы шешуіндегі С - ның нақты бір С
0
мәнін алғаннан шыққан
жалпы шешуіндегі С - ның нақты бір С
0
мәнін алғаннан шыққан
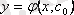 шешуі теңдеудің дербес шешуі деп аталады.
шешуі теңдеудің дербес шешуі деп аталады.
1-мысал.
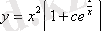 функцияны
функцияны
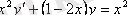 теңдеуінің шешуі бола ма?
теңдеуінің шешуі бола ма?
Шешуі:
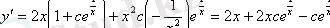
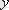 және
және
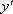 мәндерін берілген дифференциалдық теңдеуге қоямыз:
мәндерін берілген дифференциалдық теңдеуге қоямыз:
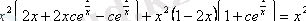
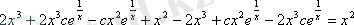
.
Соңында
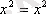 тепе - теңдігін аламыз.
тепе - теңдігін аламыз.
Олай болса,
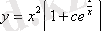 функциясы
функциясы
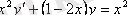 теңдеудің шешуі болады.
теңдеудің шешуі болады.
Дифференциалдық теңдеулер
Тәуелсіз айнымалы х, ізделінді функция у=у(х) және оның у', …, у(n) туындыларын байланыстыратын теңдеу дифференциалдық теңдеу (жай дифференциалдық теңдеу) деп аталады.
F(х, у, у ' , …, у (n) ) =0 (1)
Теңдеудің реті деп теңдеуге кіретін ізделінген функция туындыларының ең жоғарғы реті аталады. Егер ең жоғарғы ретті туынды шешілген болса, онда теңдеудің түрі
у (n) =f(х, у, у ' , …, у (n-1) ) (2) болады.
(2) -теңдеу ең үлкен туындыға қатысты шешілген туынды деп аталады.
Жай дифференциалдық теңдеудің шешімі деп теңдеуді қанағаттандыратын у(х) функциясын айтады.
Дифференциалдық теңдеуінің шешімінің графигін интегралдық қисық деп атайды.
Дифференциалдық теңдеудің шешімін интегралдау арқылы табамыз.
Жалпы шешімі y=φ(x, C 1 , . . . С n ) функциясы.
Жалпы интегралы F(x, C 1 , . . . С n ) =0 функциясы.
Дербес шешімі жалпы шешімдегі тұрақты С санының белгілі бір мәнінде алынады.
Коши есебі. Берілген х=х 0 болғанда у(х 0 ) =у 0 , у ' (х 0 ) = у 0 ' , …, у (n-1) (х 0 ) =у 0 n-1 болатын бастапқы шарттарды қанағаттандыратын функцияны табу Коши есебі аталады:,
Бірінші ретті дифференциалдық теңдеу мына түрде беріледі: F(x, y, y') =0 немесе y'=f(x, y) .
Жалпы шешімі y=φ(x, C), С=const.
Бірінші ретті теңдеуге Коши есебінің түрі: y'=f(х, у), у(х 0 ) =у 0. .
Екінші ретті дифференциалдық теңдеу мына түрде беріледі: F(x, y, y', y'') =0 немесе у''=f(х, у, y') .
Жалпы шешімі y=φ(x, C 1 , С 2 ), C 1 , С 2 - const.
Екінші ретті теңдеуге Коши есебінің түрі: у''=f(х, у, y'), у(х 0 ) =у 0 , y'(х 0 ) =у 0 ' .
Мысалы:
у=cosx, y'+у=0, y(0) =1
(cosx) '+cosx=0
-sinx+cosx=0
-sin0+cos0=1
1=1, болады.
y' =2х+1, y(1) =3
у=∫(2х+1) dx=x 2 +x+C жалпы шешімі.
y(1) =1 2 +1+C=3
C=1
у =x 2 +x+1 дербес шешімі.
Айнымалылары бөлінетін дифференциалдық теңдеу
M(x, у) dx + N(x, y) dy=0 дифференциалдық теңдеу берілсін.
M(x, у) =M 1 (x) M 2 (y)
N(x, y) = N 1 (x) N 2 (y) түрінде жазуға болсын.
M 1 (x) M 2 (y) dx + N 1 (x) N 2 (y) dy=0 - Айнымалылары бөлінетін дифференциалдық теңдеу.
Бұл теңдеуді N 1 (x) M 2 (y) өрнегіне бөлсек:
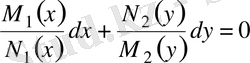 - айнамылары бөлінген теңдеу аламыз.
- айнамылары бөлінген теңдеу аламыз.
Бұл теңдеуді шешу үшін интегралдаймыз. Сонда теңдеуінің жалпы интегралы
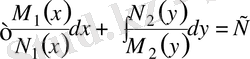 болады.
болады.
Мысалдар.
- теңдеуінің жалпы шешімін табу керек.
Шешуі: Берілген теңдеу айнымалылары бөлектенетін теңдеу.
 деп ұйғарып, теңдіктің екі жағын да у-ке бөліп,
dx
-ке көбейтейік. Сонда
деп ұйғарып, теңдіктің екі жағын да у-ке бөліп,
dx
-ке көбейтейік. Сонда
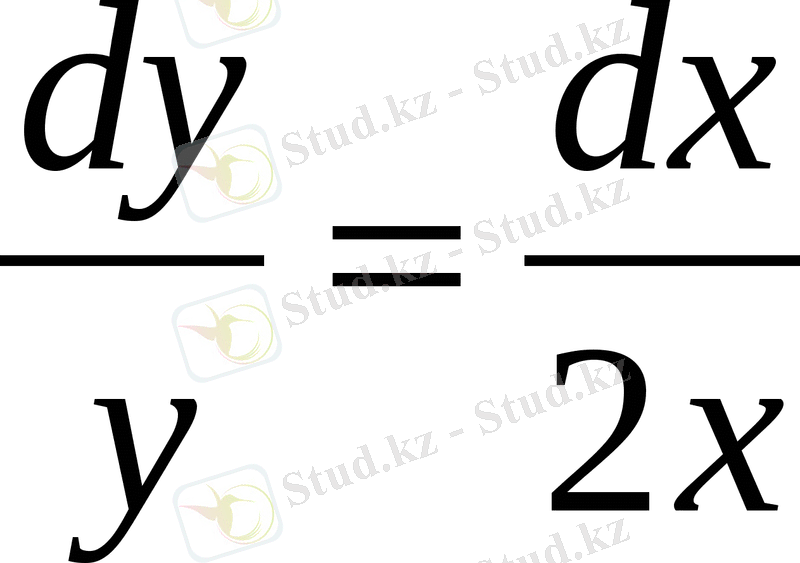 - айнымалылары бөлектенген теңдеу алынады. (9) формула бойынша теңдеудің екі жағын да интегралдасақ,
- айнымалылары бөлектенген теңдеу алынады. (9) формула бойынша теңдеудің екі жағын да интегралдасақ,
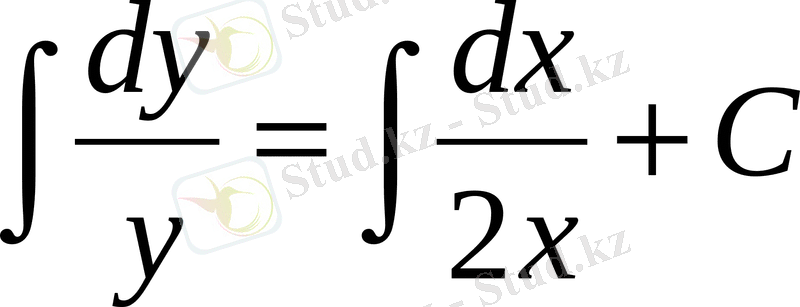 . Бұдан
. Бұдан

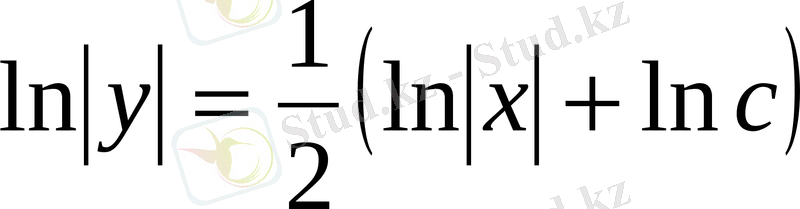 ,
,
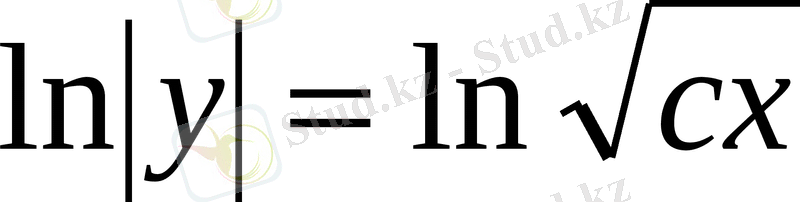 , яғни
, яғни
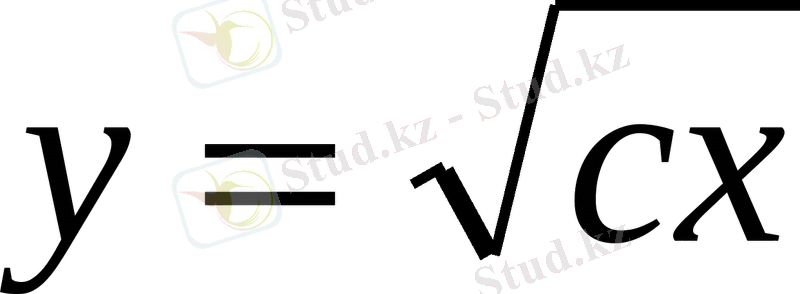 .
.
- теңдеуін интегралдау керек.
Шешуі: Дифференциалдық теңдеуді интегралдау - оның шешімін табу деген сөз.
Теңдеудің екі жағын да
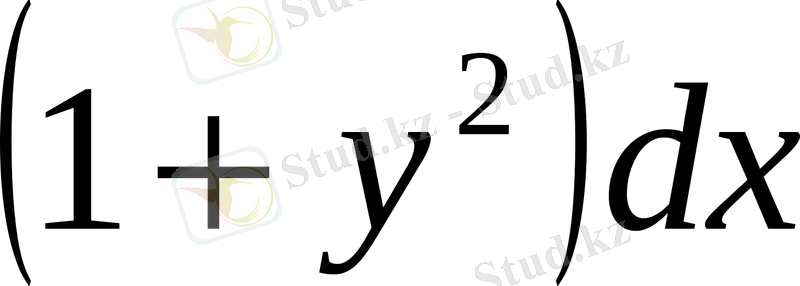 -ке көбейтіп, айнымалылары бөлектенген теңдеу аламыз:
-ке көбейтіп, айнымалылары бөлектенген теңдеу аламыз:
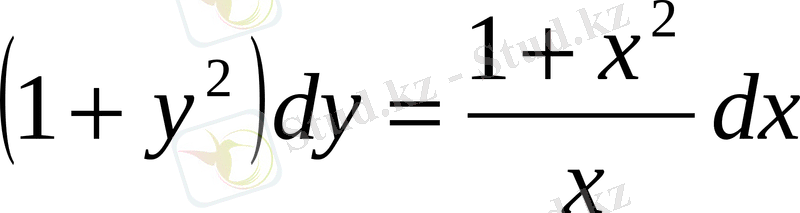 немесе
немесе
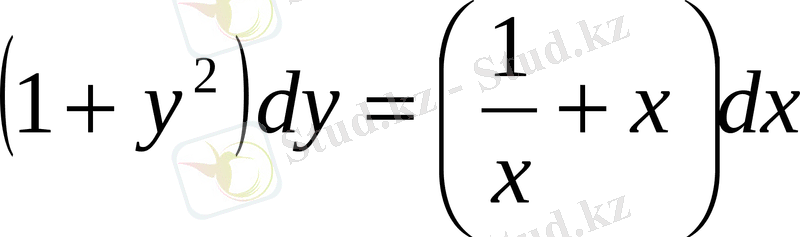 .
.
Осы теңдеуді интегралдау арқылы берілген теңдеудің жалпы шешімін табамыз:
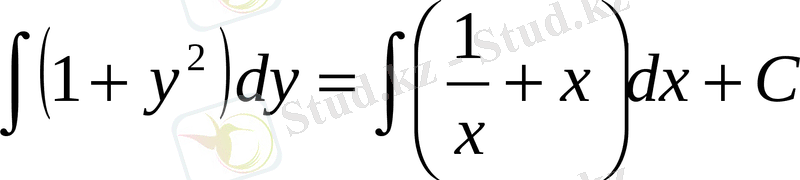 ,
,
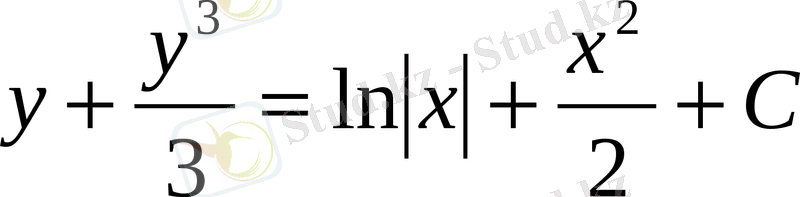 .
.
Бұдан
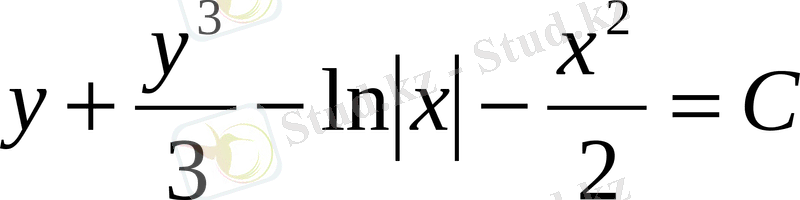 .
.
- теңдеуін шешу керек.
Шешуі: Бұл айнымалылары бөлектенетін теңдеу. Теңдеуді
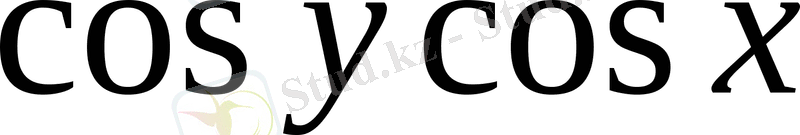 -қа бөліп (
-қа бөліп (
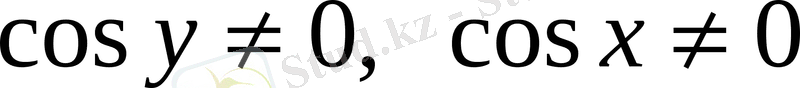 деп есептейміз), мына теңдеуді аламыз;
деп есептейміз), мына теңдеуді аламыз;
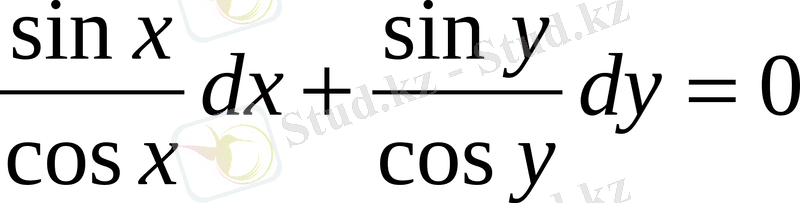
Бұдан
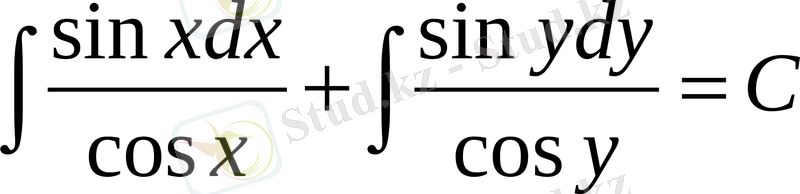 ;
;
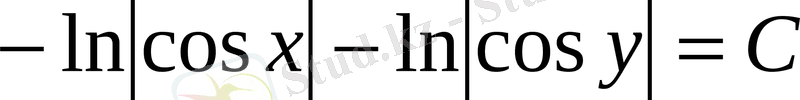 немесе
немесе
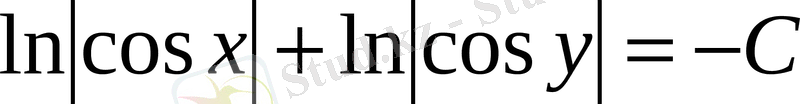 .
.
Бұл теңдеуді потенцирлеп, берілген дифференциалдық теңдеудің жалпы шешімін аламыз.
 , мұндағы
, мұндағы
 .
.
4. Бірінші ретті біртектес дифференциалдық теңдеу.
Анықтама
. Егер
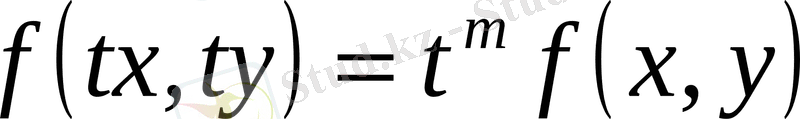 теңдігі орындалса, онда
теңдігі орындалса, онда
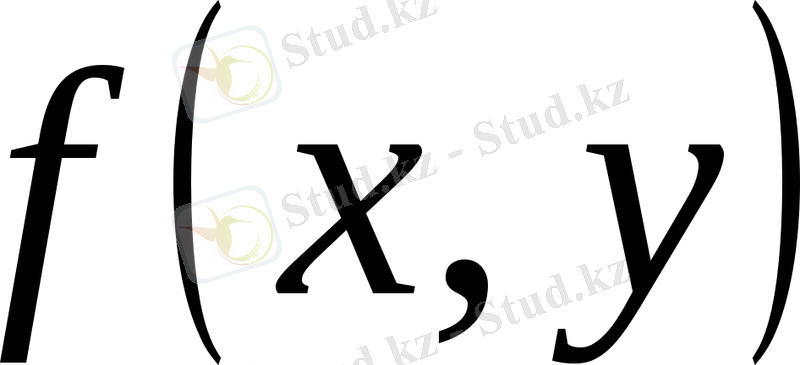 функциясы
m
өлшемді біртектес функция
деп атайды.
функциясы
m
өлшемді біртектес функция
деп атайды.
Мысал.
- функциясы үш өлшемді біртектес функция. Себебі, хжәнеуаргументтерінt-ға көбейтсек,
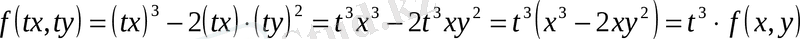
- - ноль өлшемді біртектес функция екенін көрсетейік.
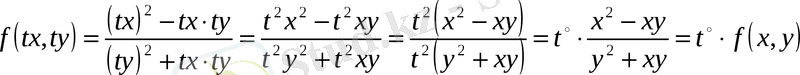
Егер
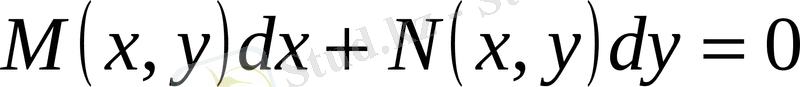 (1)
(1)
теңдеуіндегі
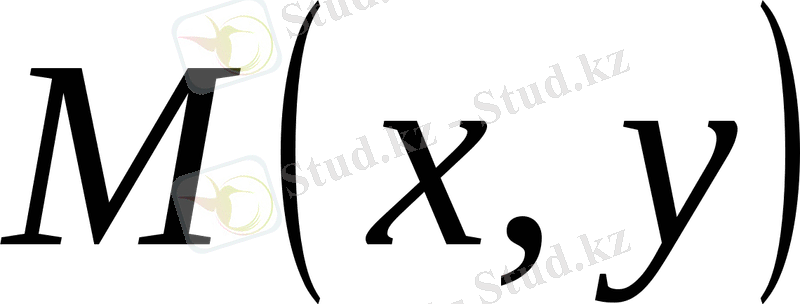 және
және
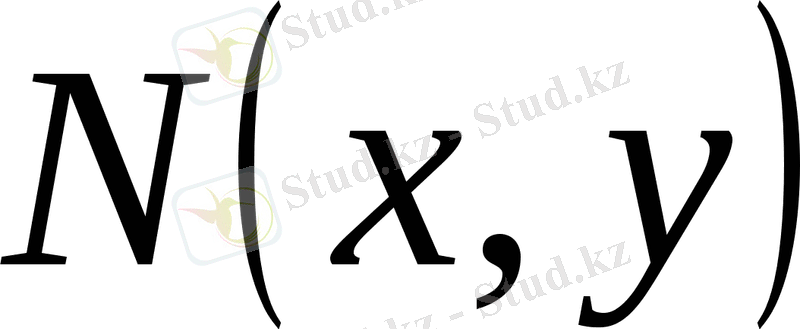 функциялары бірдей өлшемді біртектес функция болса, олда бұл теңдеу сол
өлшемді біртектес дифференциалдық теңдеу
деп аталады.
функциялары бірдей өлшемді біртектес функция болса, олда бұл теңдеу сол
өлшемді біртектес дифференциалдық теңдеу
деп аталады.
(1) теңдеуге
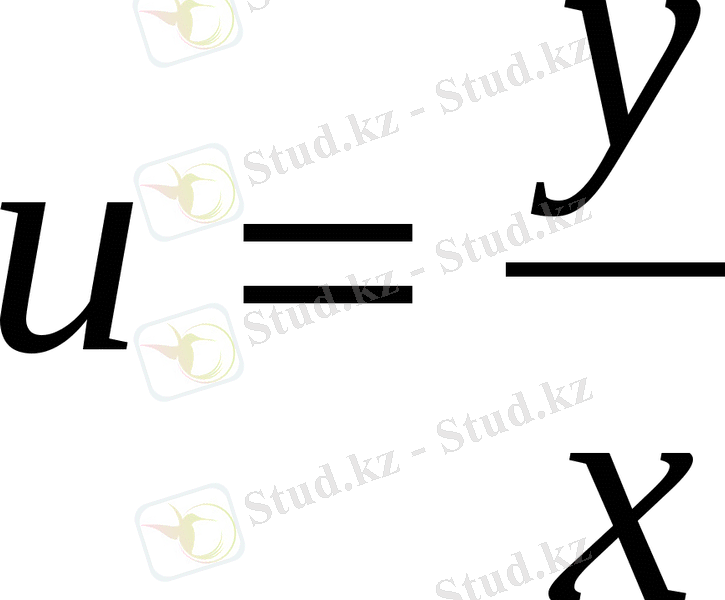 ауыстыруын қолданып, оны айнымалылары бөлектенетін теңдеуге оңай келтіруге болатынын көрсетуге болады. Мұндағы u функциясы
х
-ке тәуелді ізделінді функция. Сонда бұл ауыстырудан
ауыстыруын қолданып, оны айнымалылары бөлектенетін теңдеуге оңай келтіруге болатынын көрсетуге болады. Мұндағы u функциясы
х
-ке тәуелді ізделінді функция. Сонда бұл ауыстырудан
 , ал
, ал
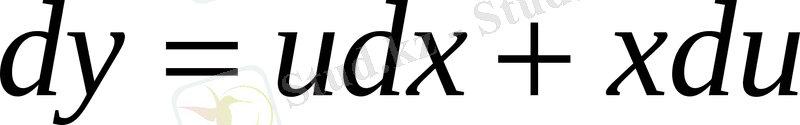 болады.
болады.
Кейбір есептерде
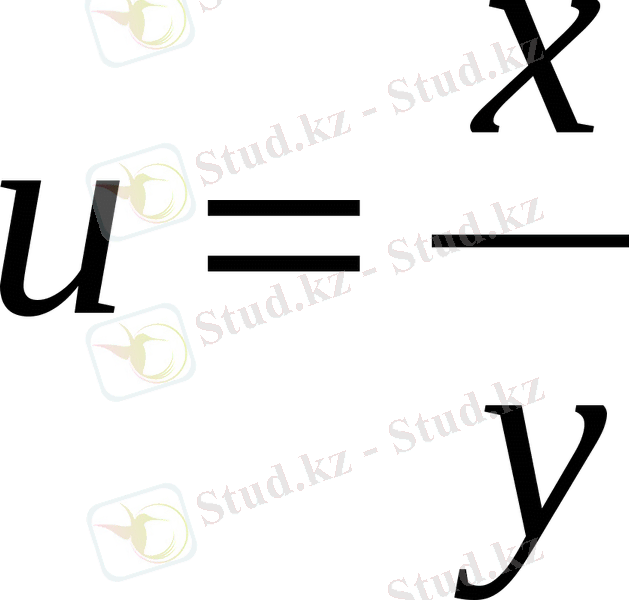 аустыруын жасау қолайлы болады.
аустыруын жасау қолайлы болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz