Алғашқы функциялар мен анықталмаған интегралдар: негізгі теоремалар, қасиеттер және қолданбалы есептер


1. Туындысы бойынша функцияны табу жөніндегі есептер.
Біз берілген туындысы бойынша функцияның өзін табумен байланысты екі есептің шешімін таппақпыз.
1. Дененің қозғалыс заңы
S=f(t)
теңдеу арқылы берілген. Бұндағы t-уақыт, s-дененің жүрген жолы. Қарастырылып отырған қозғалыстың берілген мезгілдегі лездік жылдамдығы v :
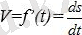
формуласы бойынша анықталатыны дифференциалдық есептеуден белгілі болатын.
Ал механикада бұған кері есеппен тым жиі кездесуге тура келеді. Ондай есептер мына түрде болып келеді; дененің берілген t мезгіліндегі туындысы v=v(t) беріледі де, сол бойынша дененің қозғалу заңын табу, яғни өткен мерзім мен жүрген жол арасындағы тәуелділікті анықтау талап етіледі. Бұл есептің шешімі былай табылады:
Берілген жылдамдық v=v(t) дененің қозғалыс заңын бейнелейтін f(t) функциясының туындысы болатыны бізге белгілі, демек ізделіп отырған белгісіз функция f(t) -тің туындысы f’(t) =v(t) берілген. Бізден сол f(t) -ті табу талап етіледі. Демек, бұл есеп дифференциалдық есептеуде қарастырылған негізгі есепке кері есеп болып табылады. Басқаша айтқанда: дифференциалдық есептеуде функция беріліп, оның туындысын табу талап етілсе, енді туынды беріледі де, бастапқы функцияны табу етіледі.
2. [0,
i
] кесіндісіне орналасқан дененің сол кесіндінің
х
нүктесіндегі
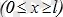 сызықтық тығыздығы
p
:
сызықтық тығыздығы
p
:
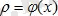
функциясы түрінде беріледі. Енді сол дененің [ 0, i ] кесіндісінің [ 0, x ] бөлігіндегі тығыздығы m -ді табу керек. [ 0, x ] бөлігінің массасы - x- тің функциясы, яғни
m=f(x) .
Олай болса, массасын табу дегеніміз осы f(x) функциясын табу болып табылады.
x нүктесіндегі сызықтық тығыздық p:
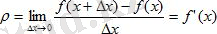
формуласымен анықталады. Ендеше,
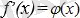
болады. Ал есептің шарты бойынша
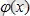 -
белгілі функция, демек берілген сызықтық тығыздығы бойынша дененің массасын табу дегеніміз берілген туынды
f’(x)
бойынша функция
f(x)
- ті табу жөніндегі мәселе болады.
-
белгілі функция, демек берілген сызықтық тығыздығы бойынша дененің массасын табу дегеніміз берілген туынды
f’(x)
бойынша функция
f(x)
- ті табу жөніндегі мәселе болады.
2. Алғашқы функция ұғымы.
Ғылым мен техниканың түрлі-түрлі салаларындағы көптеген мәселелерді шешу туындысы берілген функцияны табуға әкеліп соқтырады. Сондықтан математикада жаңа бір операция, интегралдау операциясы қарастырылады. Ізделіп отырған F(x) функциясының берілген туындысы f(x) бойынша сол F(x) функциясын табу мәселесі тек интегралдау операциясының жәрдемімен шешіледі. Міне осы F(x) - ті берілген функция f(x) -тің алғашқы функциясы деп атайды.
Анықтама. Егер бір аралықтың әрбір нүктесінде функция F(x) үшін
dF(x) =f(x) dx
теңдігі орындалса , F(x) функциясы f(x) - тің сол аралықтағы алғашқы функциясы деп аталады.
Мысалы: F(x) =x 7 бүкіл сандар осі бойында f(x) =7x 6 функциясының алғашқы функциясы болады, өйткені х-тің кез келген мәнінде (x 7 ) ’=7x 6.
Ал функция F(x) =lnx функция f(x) = 1/x үшін алғашқы функция болады
өйткені
(lnx) ’=1/x
1-теорема. Егер F(x) функциясы белгілі бір аралықта f(x) -тің алғашқы функциясы болса,
F(x) +c
Функциясыда ( C- кез келген тұрақты) ол функция үшін сол аралықта алғашқы функция болады.
Дәлеледеу: F(x) функциясы f(x) -тің алғашқы функциясы. Олай болса,
F’(x) =f(x) .
Сонымен бірге
[F(x) +C] ’=f(x)
Демек F(x) +C функциясы да f(x) үшін алғашқы функция болады.
2 теорема. Берілген функцияның алғашқы функцияларының бір-бірінен айырмасы тұрақты шама болады.
Дәлелдеу.
Егер берілген
f(x)
функциясының қандай да бір алғашқы функциясының
F(x),
ал, кез келген алғашқы функциясын
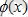 десек, онда мына шарттар орындалар еді:
десек, онда мына шарттар орындалар еді:
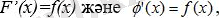
яғни алынған аралықта
F(x)
пен
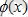 функцияларының туындылары бірдей болады. Олай болса,
функцияларының туындылары бірдей болады. Олай болса,
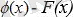 айырымы тұрақты болуы тиіс, яғни:
айырымы тұрақты болуы тиіс, яғни:
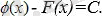
Бұдан
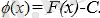
Дәлелденген екі теоремадан мынадай қорытынды шығады: егер F(x) функциясы белгілі аралықта f(x) -тің алғашқы функцияларының бірі болса, оның барлық алғашқы функцияларының жиыны f(x) +С қосындысымен өрнектеледі. Қосындының геометриялық мағнасы: f(x) -тің алғашқы функциясы F(x) - тің графигін жоғары не төмен жылжыту арқылы кез келген алғашқы функцияның графигін сала аламыз (1 сызба) .
3. Анықталмаған интеграл ұғымы
F(x) функциясы дифференциалдау деп берілген алғашқы F(x) функциясының F’(x) = f(x) туындысын немесе df(x) =f(x) dx Дифференциалын табу амалын айтамыз.
Сол амалға кері амал, яғни F’(x) болып табылатын берілген f(x) үшін алғашқы F(x) функциясын табу амалы f(x) - ті интегралдау деп аталады .
f(x) -
ті интегралдау амалын көрсету үшін
 символы қолданылады да, былай жазылады:
символы қолданылады да, былай жазылады:
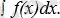
Осы
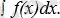 берілген
f(x)
функциясының барлық алғашқы функцияларының жиынын бейнелейді және
f(x) -
тен анықталмаған интеграл деп аталады.
берілген
f(x)
функциясының барлық алғашқы функцияларының жиынын бейнелейді және
f(x) -
тен анықталмаған интеграл деп аталады.
Демек, анықтамаға сәйкес
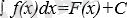
болады. Бұл формуладағы F(x) функциясы f(x) - тың белгілі бір алғашқы функциясы, С -кез келген тұрақты.
Сонымен бірге f(x) - интеграл астындағы функция, ал f(x) dx - интеграл астындағы өрнек деп аталады.
 -
символы ұзартылып алынған латын алфавитіндегі
S-
әріпі, ол символды интегралдың белгісі деп атайды.
-
символы ұзартылып алынған латын алфавитіндегі
S-
әріпі, ол символды интегралдың белгісі деп атайды.
Функцияны интегралдау және олардың алғашқы функцияларының қаиеттері жайындағы ілім интегралдық есептеу деп аталады.
Дифференциалдық есептеу сияқты интегралдық есептеуде математикалық анализдің өте маңызды бөлімдерінің бірі болып табылды. 1-параграфта қарастырылған есептердің шешуін енді интеграл түрінде былай жазуға болады:
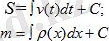
4. Анықталмаған интегралдың негізгі қасиеттері
F’(x) =f(x)
және
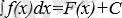 екенін ескере отырып анықталмаған интегралдың қасиеттерін қарастырамыз.
екенін ескере отырып анықталмаған интегралдың қасиеттерін қарастырамыз.
1. Дифференциалдың анықталмаған интегралы дифференциалдаған функция мен кез келген тұрақтының қосындысына тең, яғни
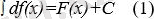
2. Анықталмаған интегралдың дифференциалын интеграл астындағы өрнекке тең, яғни
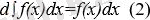
3. Тұрақты көбейткішті интегралдық белгінің алдына шығаруға да, интегралдық белгінің астына алып баруға да болады, яғни
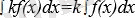
4. Бірнеше функциялардың алгебралық қосындының анықталмаған интегралы қосылғыштардан алынған анықталмаған интегралдардың алгебралық қосындысына тең, яғни
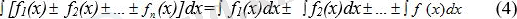
5. Анықталмаған интегралдың негізгі таблицасы
Егер u аргумент х-тің белгілі бір аралықтағы дифференциалданатын функциясы болса, берілген дифференциалдық есептеудің формулаларын пайдаланып, анықталмаған интегралдың ішіндегі негізгілерінің таблицасын жасауға болады. Бұл таблицаға енетін әрбір формуланың дұрыстығын дифференциалдау арқылы дәлелдеп көрсетуге болады.


Осы көрсетілген форуларды пайдаланып функцияның анықталмаған интегралын табуға мысалдар қарастырайық:
1.
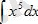 интегралын есептеу керек.
интегралын есептеу керек.
Шешуі. (3) формула бойынша
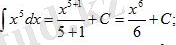
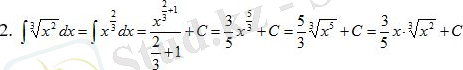
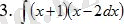 интегралын табу керек.
интегралын табу керек.
Шешуі: Интеграл астындағы өрнекті жақшаны ашып мына түрге келтіреміз:
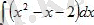
Қосындының интегралын интегралдардың қосындысымен ауыстырсақ,
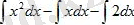 болады
болады
Үшінші интегралдағы тұрақты көбейткішті интеграл табысының алдына шығарсақ,
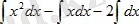 түрге келеді
түрге келеді
(2) және (3) формулаларды қолдансақ
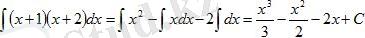
4.
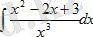 интегралын табу керек
интегралын табу керек
Шешуі: Бөлшектің алымын бөліміне мүшелеп бөліп, алдыңғы мысалдағыдай есептейміз
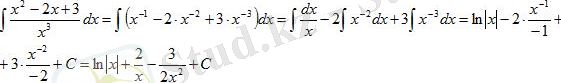
Берілген интегралды интенгралдардың қосындысына келтіріп интегралдау қосындысына келтіріп интегралдау әдісін жіктеу әдісі деп атайды.
1. 3 Типтік нұсқалардың кейбіреулерінің шешіміне талдау жасау
1.
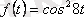 функциясының бейнесін дифференциалдау теоремасын қолдану арқылы табу керек.
функциясының бейнесін дифференциалдау теоремасын қолдану арқылы табу керек.
Шешуі:
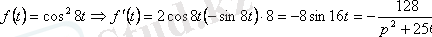 .
.
Түпнұсқаны дифференциалдау теоремасы бойынша
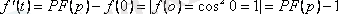
Сондықтан
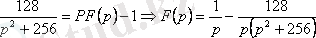
2.
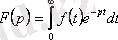 бұл
бұл
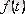 функциясының бейнесін анықтайтын формула немесе Лаплас түрлендіруі деп аталады. Осы анықтаманы пайдаланып,
функциясының бейнесін анықтайтын формула немесе Лаплас түрлендіруі деп аталады. Осы анықтаманы пайдаланып,
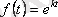 функцияның бейнесін табу керек.
функцияның бейнесін табу керек.
Шешуі:
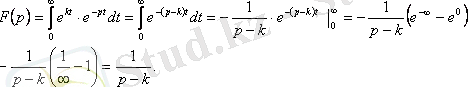
3.
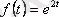 функцияның бейнесін табу керек.
функцияның бейнесін табу керек.
Шешуі:
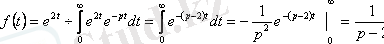 .
.
4. Берілген
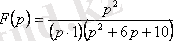 бейнесі бойынша
бейнесі бойынша
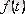 түпнұсқасын табу керек.
түпнұсқасын табу керек.
Шешуі:
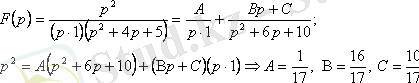
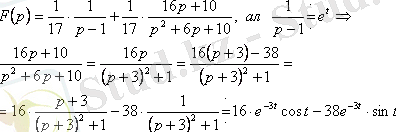
Демек,
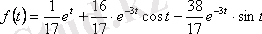
5. Берілген бейнесі бойынша
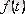 түпнұсқасын табу керек
түпнұсқасын табу керек
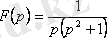
Шешуі: Түпнұсқаны интегралдау теоремасын пайдаланамыз:

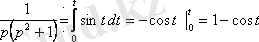 .
.
6. Дифференциалдау теоремасын пайдаланып, берілген функцияның бейнесін табу керек
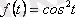 .
.
Шешуі:
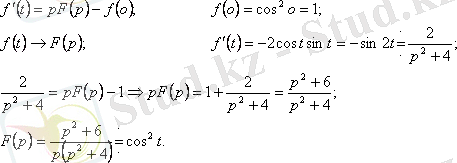
Егер
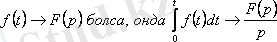 .
.
7.
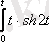 функциясының бейнесін табу керек.
функциясының бейнесін табу керек.
Шешуі:
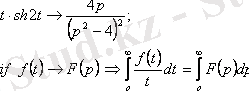
8.
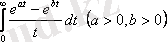 интегралын есептеу керек.
интегралын есептеу керек.
Шешуі:
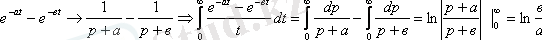
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz