Көпжақтар туралы ұғым. Екі жақты бұрыш. Кеңістіктегі симметрия. Дұрыс көпжақ ұғымы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Көпжақтар туралы ұғым.

Екі жақты бұрыш.

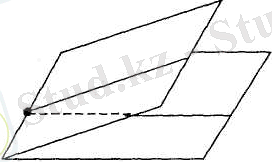
Ортақ түзумен шенелген екі жарты жазықтықтан жасалған бұрыш екі жақты бұрыш деп аталады. (1-сызба)

1-сызба 2-сызба

Жарты жазықтықтар оның қабырғалары, ал оларды шенейтін түзу екі жақты бұрыштыц қыры деп аталады.

Екі жақты бұрыштың қырына перпендикуляр жазықтық оның қабырғаларын екі сәуле бойымен қияды. Осы сәулелерден пайда болған бұрыш екі жақты бұрыштың сызықтық бұрышы деп аталады.

Екі жақты бұрыштың шамасы оның сызықтық бұрышынның шамасына тең болады.

Сондықтан екі жақты бұрыштың шамасы оның сызықтық бұрышын таңдауға тәуелді емес.

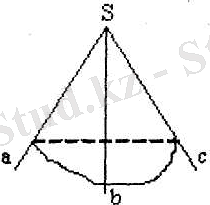
Бір S нүктесінен шығып, бір жазықтықта жатпайтын а, b, с сәулері берілсін.

(aSb), (aSc), (bSc) жазық бұрыштарынан құралған фигура үшжақты бұрыш деп аталып, (abc) түрінде белгіленеді. (2 - сызба)

Бұл бұрыштар үшжақты жақтары деп, ал сәулелер оның қырлары деп аталады. Жазық бұрыштардың ортақ төбесі S үшжақты бұрыштын төбесі деп аталады. Оның жақтары арқылы жасалған екіжакты бұрыштар үшжақты бұрыштың екіжақты бұрышы деп аталады.

Стереометрияда дене деп аталатын кеңістіктік фигуралар зерттеледі. Дене - бетпен шектелген кеңістіктің бөлігі болып табылады.

a)
Тетраэдр

a)Тетраэдр: 67 б)-сурет

б)
Параллелепипед
1-сурет

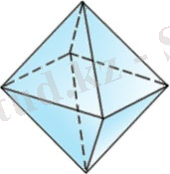
a)Тетраэдр: 68-сурет

Октаэдр
2-сурет

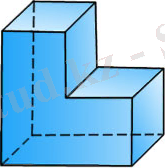
Дөңес емес көпжақ
3-сурет

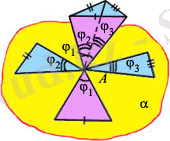
Дөңес емес көпжақ3-сурет: 70-сурет

j ₁ + j ₂ + j ₃ < 360 ^o
4-сурет

Көпбұрыштардан тұратын жөне кандай да бір геометриялык денені шектейтін бетті көпжакты бет немесе көпжақ деп атайтын боламыз. Көпжақтың мысалдары - тетраэдр жене параллелепипед. 68-суретте тағы бір көпжақ - октаэдр кескінделген. Ол сегіз үшбұрыштан тұрады. Көпжақпен шектелген денені де көбінесе көпжақ деп атайды.
Көпжақты күрайтын көпбұрыштар оның жақтары деп аталады. Тетраэдр мен октаэдрдің жақтары - үшбұрыштар (1, а және 2-сурет), ал параллелепипедтің жақтары - параллелограмдар (1, б -сурет) болып табылады. Жактардың кабырғалары - көпжақтың қырлары , ал қырлардың ұштары - төбелері деп аталады. Бір жаққа жатпайтын екі төбені қосатын кесінді көпжақтың диагоналі деп аталады.
Көпжақтар дөңес және дөңес емес болады. Егер көпжақ оның әрбір жағы жазықтығының бір жағында жатса, онда ол көпжақ дөңес деп аталады. Тетраэдр, параллелепипед жөне октаэдр дөңес көпжактарға жатады. 3-суретте сегіз көпбұрыштан тұратын дөңес емес көпжақ кескінделген.
Дөңес көпжақтың барлық жақтары дөңес көпбұрыштар болатыны анық. Дөңес көпжақтың әрбір төбесіндегі барлық жазық бұрыш-тардың қосындысы З60°-тан кем екенін дөлелдеуге болады. 3 -сурет бойынша бұл тұжырым былай анықталады: көпжақ қырлары бойымен "кесілген" де, оның ортақ А төбесіндегі барлық жақтары бір a жазықтығында орналасатындай етіп жазылған. А төбесіндегі барлық жазық бұрыштардың қосындысы, яғни j ₁ + j ₂ + j ₃ , 360° -тан кем екені көрініп тұр.

Кеңістіктегі симметрия.

a):

б)

a):

в)
77-сурет

a):

б)

a):

в)
78-сурет

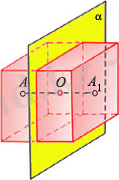
Біз планиметрияда нүктеге катысты және түзуге қатысты симметриялы фигураларды карастырдық. Стереометрияда нүктеге, түзуге жөне жазыктыққа қатысты симметрияны қарастырады.
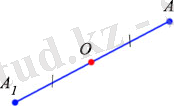
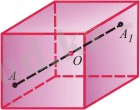
Егер O - АА ₁ кесіндісінің ортасы болса, А мен А ₁ нүктелері О нүктесіне қатысты симметриялы нүктелер деп аталады (0 - симметрия центрі) (77, а-сурет) . О нүктесі өзіне-өзі симметриялы болып саналады.
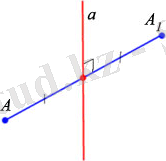
Егер а түзуі АА ₁ кесіндісінің ортасы арқылы өтсе және осы кесіндіге перпендикуляр болса, А мен А ₁ нүктелері а тузуіне (симметрия осі) қатысты симметриялы деп аталады (77, б-сурет) . а түзуінің өрбір нүктесі өзіне-өзі симметриялы болып саналады.
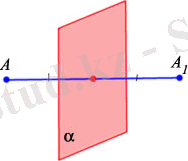
Егер a жазықтығы АА ₁ кесіндісінің ортасы арқылы өтсе жөне осы кесіндіге перпендикуляр болса, А мен А ₁ нүктелері a жазъқтығына (симметрия жазықтығы ) қатысты симметриялы деп аталады. (77, в-сурет) a жазықтығының әрбір нүктесі өзіне өзі симметриялы болып саналады.
Фигураның симметрия центрі, осі жөне жазықтьны ұғымдарын енгізейік.
Егер фигураның әрбір нүктесі осы фигураның қандай да бір нүктесіне (түзуіне, жазықтығына) қатысты симметриялы болса, осы нүкте (түзу, жазықтық) фигураның симметрия центрі (осі, жазықтығы) деп аталады.
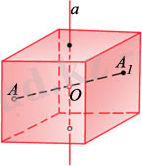
78 а, б, в-суретте тікбұрышты параллелепипедтің О симметрия центрі, а осі жөне a жазықтығы көрсетілген. Фигураның бір немесе бірнеше симметрия центрлері (симметрия осьтері, симметрия жазықтықтары) болуы мүмкін. Мысалы, кубтың бір ғана симметрия центрі жөне бірнеше симметрия осьтері, симметрия жазықтықтары бар. Шексіз көп симметрия центрлері, осьтері жөне жазықтықтары болатын фигуралар бар. Мүндай фигуралардың ең қарапайым түрі түзу мен жазықтық болып табылады. Жазықтықтың кез келген нүктесі оның симметрия центрі болып табылады. Берілген жазыктыққа перпендикуляр кез келген түзу (жазықтық) оның симметрия осі (жазықтығы) болып табылады. Сонымен қатар, симметрия центрлері, осьтері, жазықтықтары жоқ болатын фигуралар да бар. Мысалы, тетраэдрдің бірде бір симметрия центрі болмайды.
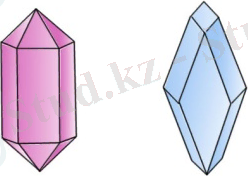
Табиғатта, сәулет өнерінде, техникада, тұрмыста симметрияны көп кездестіреміз. Көптеген үйлер, ғимараттар жазықтыққа қатысты симметриялы (79-сурет), детальдардың да кейбір түрлерінің симметрия осі бар болады. Табиғатта кездесетін кристалдардың барлығының дерлік симметрия центрі, осі жөне жазықтыгы бар (80-сурет) . Геометрияда көпжактың симметрия центрі, осі жөне жазыктығы осы көпжақтың симметрия элементтері деп аталады.

: 79-сурет

: 80-сурет

Дұрыс көпжақ ұғымы.

81-сурет

81-сурет:

82-сурет

81-сурет:

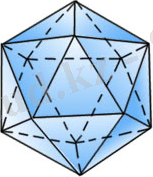
83-сурет

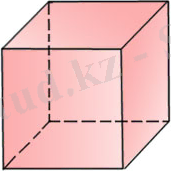
84-сурет

84-сурет:

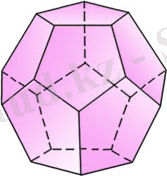
85-сурет

Егер дөңес көпжактың барлық жақтары тең дүрыс көпбұрыштар болса, сонымен қатар оның әрбір төбесінде саны бірдей қырлар тоғысатын болса, ондай дөңес көпжақ дұрыс көпжақ деп аталады. Мысалы, куб дүрыс көпжак болып табылады. Оның барлық жақтары тең квадраттар жөне әр төбесінде үш қыр тоғысады.
Дүрыс көпжақтың барлық қырлары бір-біріне тең екені көрініп тұр. Қыры ортақ екі жақты қамтитын барлық екіжақты бұрыштар да тең екенін дөлелдеуге болады.
Жақтары дұрыс алтыбұрыш, жетібұрыш жопе жалпы п $C:\Program Files\Геометрия\Геометрия 10 сынып\Teory\teory\images\b=.jpg$ 6 болғанда п-бұрыш болатын дұрыс көпжақ болмайтынын дөлелдейік. Шынында да, n-бұрыштың n $C:\Program Files\Геометрия\Геометрия 10 сынып\Teory\teory\images\b=.jpg$ 6 болғанда бұрышы 120 ⁰ -тан кіші болмайды (неге екенін түсіндіріңдер) . Екінші жагынан, көпжақтың өрбір төбесінде үштен кем жазык бұрыш болмауы тиіс, Сондықтан, егер жақтары n $C:\Program Files\Геометрия\Геометрия 10 сынып\Teory\teory\images\b=.jpg$ 6 болғанда дүрыс n-бұрыш болатын дүрыс көпжақ бар болса, онда мұндай көпжактың әрбір төбесіндегі жазық бұрыштарының қосындысы 120 ^{0

.} 3 = 360 -тан кіші болмас еді. Бірақ бұл мүмкін емес, өйткені дөңес көпжактың өрбір төбесіндегі барлық жазык бұрыштардың қосындысы 360 ⁰ -тан кіші (25-п) .
Осы себепті дүрыс көпжактың өрбір төбесі үш, төрт немесе бес теңқабырғалы үшбұрыштардың, не үш квадраттың, не үш дүрыс бесбұрыштың төбесі болуы мүмкін. Басқа мүмкін жағдай жоқ.
Осыған сөйкес мынадай дүрыс көпжақтар аламыз:
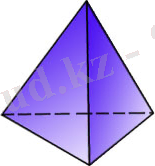
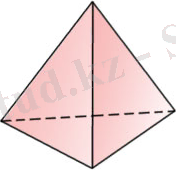
Дұрыс тетраздр (біз дұрыс тетраэдр мен дұрыс үшбұрышты пирамиданы ажыратып айтамыз. Барлық қырлары тең дұрыс тетраэдрден дүрыс үшбұрышты пирамиданың өзгешелігі онъщ бүйір қырлары бір-біріне тен болғанмен, олар табанының кабырға-ларына тең болмауы мүмкін. ) (81-сурет) төрт теңқабырғалы үшбұрыштан тұрады. Оның әрбір төбесі үш үшбұрыштың төбесі болып табылады. Демек, әрбір төбедегі жазық бұрыштардың қосындысы 180°-қа тең.
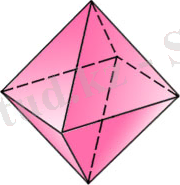
Дұрыс октаэдр (82-сурет) сегіз теңқабырғалы үшбұрыштан құралған. Октаэдрдің өрбір төбесі төрт үшбұрыштың төбесі болып табылады. Демек, өрбір төбедегі жазык бұрыштардың қосындысы 240 ⁰ -ка тең.
Дұрыс икосаэдр (83-сурет) жиырма тең қабырғалы үшбұрыштан құралған. Икосаэдрдің әрбір төбесі бес үшбұрыштың төбесі болып табылады. Ендеше, әрбір төбедегі жазық бұрыштардың қосындысы 300 ⁰ -қа тең.
Куб (84-сурет) алты квадраттан құралған. Кубтың әрбір төбесі үш квадраттың төбесі болып табылады, Ендеше, өрбір төбедегі жазық бұрыштардың қосындысы 270°-қа тең.
Дұрыс додекаэдр (85-сурет) он екі дұрыс бесбұрыштан күралған. Додекаэдрдің әрбір төбесі үш дүрыс бесбұрыштың төбесі болып табылады, Ендеше, өрбір төбедегі жазық бұрыштардың қосындысы 324 ⁰ -қа тең.
Дұрыс көпжақтардың осы аталып өткен бес түрінен басқа түрлері жоқ.

Дұрыс көпжақтардың симметрия элементтері.

Дүрыс көпжактардың симметрия элементтерін карастырайық.
Дұрыс тетраэдрдің симметрия центрі жок болады. Дұрыс тетраэдрдің үш симметрия осі жөне алты симметрия жазықтығы бар.

Куб диагональдарының қиылысу нүктесі - оның жалғыз ғана симметрия центрі болып табылады. Кубтың тоғыз симметрия осі бар. Барлық симметрия осьтері симметрия центрі арқылы өтеді. Кубтың тоғыз симметрия жазықтығы бар. Дұрыс октаэдрдің және дұрыс додекаэдрдің симметрия центрі мен бірнеше симметрия осі және жазықтықтары бар.

Геометриялық дене.

a)
Тетраэдр

a)Тетраэдр: 67 б)-сурет

б)
Параллелепипед
1-сурет

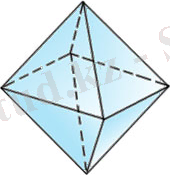
a)Тетраэдр: 68-сурет

Октаэдр
2-сурет

Біз көпжақ қандай да бір геометриялық денені шектейді деп атап көрсеттік. Осы түсінікті анықтайык.
М нүктесіне мейліншее жақын жатқан көп нүктенің (оның өзін қоса алғанда) арасында F фигурасына тиісті де, тиісті емес те нүктелер бар болатын жағдайда М нүктесі берілген F фигурасының шекаралық нүктесі деп аталады. Фигураның барлық шекаралық нүктелер жиыны оның шекарасы деп аталады. Мысалы, шардың шекарасы сфера болады.
Фигураның шекаралық нүкте болмайтын нүктесі фигураның ішкі нүктесі деп аталады. Фигураның әрбір ішкі нүктесі кеңістікте осы нүктеге мейлінше жақын жатқан нүктелер де фигураға тиісті болатындығымен сипатталады. Мысалы, шардың сферасына, яғни оның шекарасына жатпайтын кез келген нүктесі шардың ішкі нүктесі болып табылады.
Егер фигураны кандай да бір сферамен қоршау мүмкін болса, ондай фигура шектелген фигура деп аталады. Шар, тетраэдр, параллелепипед - шектелген, ал түзу мен жазықтық - шектелмеген фигуралар.
Егер фигураның кез келген екі нүктесін тұтасымен сол фигурада жататындай үзіліссіз сызыкпен қосу мүмкін болса, ол байланысқан фигура деп аталады. Мысалы, тетраэдр (1, а -суретті кара), параллелепипед (1, б -суретті кара), октаэдр (2-суретті кара), жазықтық байланысқан фигуралар болып табылады. Параллель екі жазықтықтан тұратын фигура байланыскан фигура емес.
Кеңістіктегі шектелген байланысқан фигураны геометриялық дене деп (немесе дене деп) атайды, ол өзінің шекаралық нүктелерін, өрі шекаралық нүктеге мейлінше жақын - толып жаткан ішкі нүктелерді камтиды. Дененің шекарасын оның беті деп те атайды жөне бет денені шектеп тұр дейді.
Жазыктықтың екі жағын ала берілген дененің нүктелері жатса, оны қиюшы жазықтық деп атайды. Денені жазықтықпен киюдан пайда болған фигура (яғни дененің қиюшы жазықтықпен ортак бөлігі) дененің қимасы деп аталады.

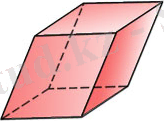
Призма

Призма. A ₁ A ₂ A ₃ . . . A _n мен B ₁ B ₂ B ₃ . . . B _n
көпбұрыштары - призманың
табандары. A ₁ A ₂ B ₂ B ₁ , . . . , A _n A ₁ B ₁ B _n
параллелограмдары - бүйір жақтары
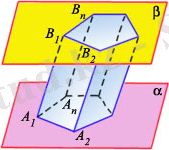
71-сурет

Призма. A1A2A3. . . Anмен B1B2B3. . . Bnкөпбұрыштары - призманыңтабандары. A1A2B2B1, . . . , AnA1B1Bnпараллелограмдары - бүйір жақтары71-сурет:

72-сурет

a мен b параллель жазықтықтарында орналаскан өзара тең A ₁ А ₂ , . . . А _n мен В ₁ В ₂ . . . В _n көпбұрыштарын карастырайык (71-сурет), олардың сөйкес төбелерін қосатын кесінділері параллель.

А ₁ А ₂ В ₂ В ₁ , А ₂ А ₃ В ₃ В ₂ , . . . , А _n А ₁ В ₁ В _n (1)

n төртбұрыштың карама-қарсы қабырғалары қос-қостан параллель болғандыктан, өрқайсысы параллелограмм болып табылады. Мысалы, А ₁ А ₂ В ₂ В ₁ төртбұрышының А ₁ В ₁ мен А ₂ В ₂ қабырғалары шарт бойынша параллель, ал А ₁ А ₂ мен В ₁ В ₂ кабырғалары параллель жазықтықтарды үшінші жазықтықпен киғандағы қасиет бойынша параллель (11-п. )
Параллель жазықтықтарда орналасқан өзара тең А ₁ А ₂ . . . А _n және В ₁ В ₂ . . . В _n көпбұрыштары мен (1) n параллелограмнан құралған көпжақ призма деп аталады (71-суретті кара) .
А ₁ А ₂ . . . А _n мен В ₁ В ₂ . . . В _n көпбұрыштары призманың табандары , ал (1) параллелограмдар - бүйір жақтары деп аталады. А ₁ В ₁ , А ₂ В ₂ . . . , А _n В _n кесінділері призманың бүйір қырлары деп аталады. Бұл қырлар бір-біріне тізбектей жалғаскан (1) параллелограмдардың қарама-қарсы кабыргалары ретінде тең жөне параллель. Табандары А ₁ А ₂ . . . А _n және В ₁ В ₂ . . . В _n болатын призманы А ₁ А ₂ . . . А _n В ₁ В ₂ . . . 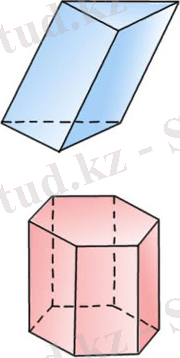В _n деп белгілейді де, n-бұрышты призма деп атайды. 72-суретте үшбұрышты және алтыбұрышты призмалар, ал 67, б-суретте -төртбұрышты призма, яғни параллелепипед кескінделген.
Призма табанының қандай да бір нүктесінен екінші табаны жазықтыгына жүргізілген перлендикуляр пркзманың биіктігі деп аталады.
Егер призманың бүйір қырлары табандарына перпендикуляр болса, ол - тік призма деп, ал баскаша болған жагдайда көлбей призма деп аталады. Тік призманың биіктігі оның бүйір қырына тең.
Егер тік призманың табандары дүрыс көпбұрыштар болса, оны дұрыс призма деп атайды. Мүндай призманың барлық бүйір жақтары - тең тіктөртбұрыштар (неге екенін түсіндіріңдер) . 72-суретте алтыбұрышты дүрыс призма кескінделген.
Призманың барлық жақтары аудандарының қосындысы оның толық бетінің ауданы деп, ал оның бүйір жақтары аудандарының қосындысы призманың бүйір бетінің ауданы деп аталады. Толық беттің S _тб ауданы бүйір бетінің S _бб ауданы мен призманың S _таб табандары ауданының формуласы арқылы өрнектеледі:

S _тб = S _бб +2 S _таб

Тік призманың бүйір бетінің ауданы туралы теореманы дөлелдейік.

Теорема
Тік призманың бүйір бетінің ауданы табанының периметрін призманың биіктігіне көбейткенге тең.

Тіктөртбұрышты параллелепипедтің табан кабыргалары 12 см жөне 5 см-ге тең. Параллелепипедтің диагоналі табан жазықтығымен 45° бұрыш жасайды. Параллелепипедтің бүйір қырын табыңдар. 13 см.
Тік параллелепипедтің табаны диагональдары 10 см жөне 24 см-ге тең ромб болып табылады, ал параллелепипедтің биіктігі 10 см-ге тен. Параллелепипедтің үлкен диагоналін табыңдар.

26 см.

Дүрыс үшбұрышты призманың табан кабырғасы 8 см-ге, бүйір қыры 6 см-ге тең. Призманың жоғарғы табанының кабырғасы мен төменгі табанының қарама-қарсы төбесі арқылы өтетін қиманың ауданын табыңдар. 8см2.
Тік призманың табаны тең бүйірлі трапеция, оның табандары 25 см жөне 9 см, биіктігі 8 см-ге тең. Призманың бүйір қырларындағы екіжақты бұрыштарды табыңдар. 45°, 135°, 45°, 135°.
Кубтың қарама-қарсы жатқан екі қыры арқылы ауданы 64 см2-ге тең кима жүргізілген. Кубтың қырын жөне оның диагоналін табыңдар. 8 см и 8см.
Дұрыс төртбұрышты призманың диагоналі табан жазықтығына 60° бұрышпен көлбеген. Егер табанының диагоналі 4 см болса, оның төменгі табанының кабыргасы мен жоғары табанының қарама-карсы кабырғасы арқылы өтетін қиманың ауданын табыңдар. 16 см2.
Дүрыс төртбұрышты призманың диагоналі бүйір жагының жазықтығымен 30° бұрыш жасайды. Диагональ мен табан жазықтыгының арасындағы бұрышты табыңдар. 45°.
Дүрыс төртбұрышты призма табанының диагоналі арқылы призманың диагоналіне параллель кима жүргізілген. Егер призма табанының қабыргасы 2 см-ге, ал оның биіктігі 4 см-ге тең болса, қиманың ауданын табыңдар. 2см2.
Тік призманың табаны - қабырғалары 5 см жөне 3 см, ал олардың арасындағы бұрыш 120°-қа тең үшбұрыш. Бүйір жақта-рының ең үлкенінің ауданы 35 см2-ге тең. Призманың бүйір бетінің ауданын табыңдар. 75 см2.
Тік параллелепипедтің табан қабыргалары 8 см жөне 15 см жөне олар бір-бірімен 60° бұрыш жасайды. Диагональдык кималарының ең кішісі 130 см2-ге тең. Параллелепипед бетінің ауданын табыңдар. 20 (23 + 6) см2.
АВСА1В1С1тік призмасының табаны -Вбұрышы тік болып келген тікбұрыштыАВСүшбұрышы. ВВ1қыры аркылыАА1С1Сжағы жазыктығына жүргізілген. ЕгерАА1= 10 см, АD= 27 см, DС= 12 см болса, киманың ауданын табыңдар. 180 см2.
Тік призманың табаны тікбұрышты үшбұрыш болып табылады. Гипотенузаның ортасы аркылы осы гипотенузаға перпен-дикуляр жазыктык жүргізілген. Егер катеттер 20 см жөне 21 см-ге, ал бүйір қыры 42 см-ге тең болса, қиманың ауданын табыңдар. 580 см2.
Үшбұрышты көлбеу призманың екі бүйір жағы өзара перпен-дикуляр, ал олардың баска екі бүйір қырларынан 12 см және 35 см кашықтықта түрған ортақ қыры 24 см. Призманың бүйір бетінің ауданын табыңдар. 2016 см2.