Бессель функциялары: анықтамасы, қасиеттері және математикалық физика есептеріндегі қолданылуы


Бессель функцияларын анықтау және оларды математикалық физика есептерін шешуде қолдану
Смагулова С. С.
студент, ПМПУ, Павлодар қ.
Машрапов Н. Қ.
профессор, ПМПУ, Павлодар қ.
Математикалық физиканың негізгі бөлімдеріне жататын және нақты техникалық сұрақтарға жауап беруге негізделген көптеген мәселелердің шешімі Бессель функцияларын қолдануымен байланысты. Бессель функциялары акустика, радиофизика, гидродинамика, атомдық және ядролық физика есептерін шешуде кеңінен қолданылады. Сонымен бірге Бессель функциялары жылуөткізгіштік және серпімділік теорияларында кездеседі (пластинкалар тербелісі, қабықшалар теориясы, сызаттардың жанында кернеу концентрациясын анықтау туралы есептер) .
Бессель теңдеуі деп коэффициенттері айнымалы болатын, мынадай екінші ретті сызықтық дифференциалды теңдеуді айтамыз:
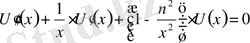 (1)
(1)
Бұл теңдеу Бессельдің теңдеуі деп аталады, ал оны қанағаттандыратын функциялар, яғни оның интегралдары Бессельдің функциялары болып табылады. (1) -теңдеу
 -ретті сызықтық теңдеу болғандықтан, оның жалпы шешімі мынадай түрде жазылады:
-ретті сызықтық теңдеу болғандықтан, оның жалпы шешімі мынадай түрде жазылады:
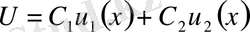 .
.
Мұндағы
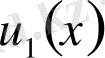 және
және
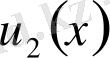 - екі тәуелсіз дербес шешімдер, ал
- екі тәуелсіз дербес шешімдер, ал
 және
және
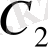 - еркін тұрақтылар.
- еркін тұрақтылар.
Мысал. Бессель функцияларын гармоникалық функциялар теориясына қолданайық.
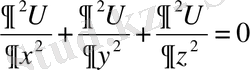 (1)
(1)
Шешуі: Ең алдымен цилиндрлік координаталарды енгізейік:
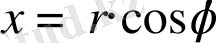 ,
,
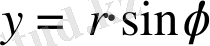 ,
,
 (2)
(2)
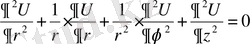 (3)
(3)
 , Бұл жерде
, Бұл жерде
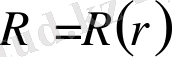 ,
,
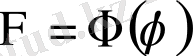 ,
,
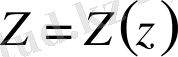 (4)
(4)
(4) -өрнекті (3) -теңдеуге қойсақ:
 (5)
(5)
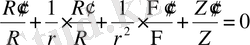 (6)
(6)
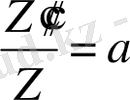 (7)
(7)
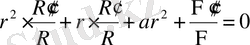 (8)
(8)
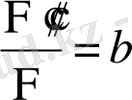 (9)
(9)
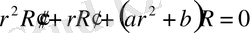 (10)
(10)
 функцияларының сипаты
функцияларының сипаты
 тұрақтыларының таңбасына байланысты. Тәуелсіз
тұрақтыларының таңбасына байланысты. Тәуелсіз
 айнымалының абсолют мәнінің шексіз өсуімен
айнымалының абсолют мәнінің шексіз өсуімен
 функциясы және
функциясы және
 шексіз артады. Әдетте
шексіз артады. Әдетте
 өзгерісінің мұндай сипаты физикалық себептерге байланысты қабылданбайды, сондықтан
өзгерісінің мұндай сипаты физикалық себептерге байланысты қабылданбайды, сондықтан
 -ны теріс деп санаймыз:
-ны теріс деп санаймыз:
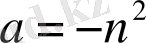 , онда
, онда
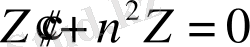
Егер бұл теңдеуді интегралдасақ, сонда
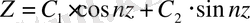 (11)
(11)
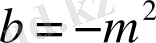 болсын, онда
болсын, онда
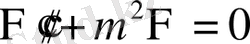
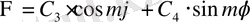 (12)
(12)
Осыдан
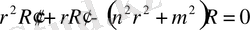 (13)
(13)
(13) -теңдеу,
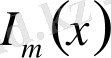 функциясы қанағаттандыратын теңдеуге ұқсас болып келеді:
функциясы қанағаттандыратын теңдеуге ұқсас болып келеді:
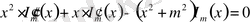 (14)
(14)
Егер (13) -теңдеуге келесі шамаларды енгізсек:
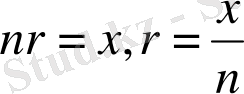 онда
онда
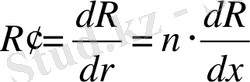 ,
,
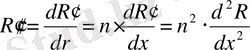
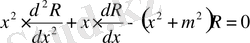 (15)
(15)
Осыдан
(16)
 -ті тауып бір-біріне көбейткеннен кейін Лаплас теңдеуінің дербес интегралын аламыз. Бұл жерде
-ті тауып бір-біріне көбейткеннен кейін Лаплас теңдеуінің дербес интегралын аламыз. Бұл жерде
 коэффициенттері және
коэффициенттері және
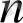 шамасы кез-келген мәндерді қабылдай алады, ал
шамасы кез-келген мәндерді қабылдай алады, ал
 кез-келген бүтін сан бола алады. Осылайша бұл Лаплас теңдеуінің сансыз көп интегралдарын табуға мүмкіндік береді. Оларды еркін тұрақтыларға көбейтіп, жинақтап болған соң жалпы интегралды таба аламыз. Осыған мысал ретінде келесі есепті қарастырайық.
кез-келген бүтін сан бола алады. Осылайша бұл Лаплас теңдеуінің сансыз көп интегралдарын табуға мүмкіндік береді. Оларды еркін тұрақтыларға көбейтіп, жинақтап болған соң жалпы интегралды таба аламыз. Осыған мысал ретінде келесі есепті қарастырайық.
Мысал. Бессель функцияларын жылулық тепе-теңдікке арналған есебінде қолданайық.
Осі
 өсі бойынша, ал радиусы 1-ге тең цилиндрден тыс орналасқан және
өсі бойынша, ал радиусы 1-ге тең цилиндрден тыс орналасқан және
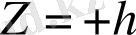 және
және
 кеңістіктегі екі жазықтықтың арасындағы қалыптасқан температураның таралуын анықтау керек болсын. Сонымен қатар жоғарғы және төменгі жазықтықтардағы температура 0-ге, ал цилиндрдің бетіндегі температура тұрақты
кеңістіктегі екі жазықтықтың арасындағы қалыптасқан температураның таралуын анықтау керек болсын. Сонымен қатар жоғарғы және төменгі жазықтықтардағы температура 0-ге, ал цилиндрдің бетіндегі температура тұрақты
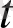 деңгейде деп есептейік.
деңгейде деп есептейік.
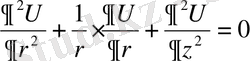 (1)
(1)
Шешуі:
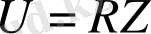 ,
,
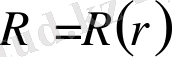 ,
,
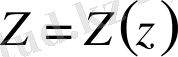 .
.
 және
және
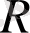 келесі теңдеуді қанағаттандыруы қажет:
келесі теңдеуді қанағаттандыруы қажет:
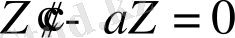 ,
,
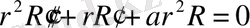 (2)
(2)
Егер
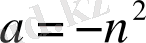 , онда (2) -теңдеудің дербес шешімі келесі түрде жазылады:
, онда (2) -теңдеудің дербес шешімі келесі түрде жазылады:
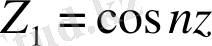 ,
,
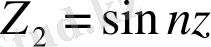 ,
,
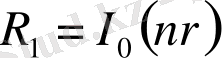 ,
,
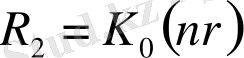 (3)
(3)
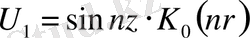 ,
,
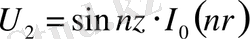 ,
,
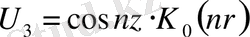 ,
,
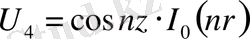 ; (4)
; (4)
Осылайша (1) -теңдеудің
 интегралын жалпы формада таба аламыз.
интегралын жалпы формада таба аламыз.
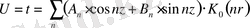 (5)
(5)
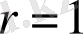 болғандағы:
болғандағы:
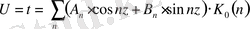 (6)
(6)
Бұл теңдеу функцияның Фурье қатарының жіктелуіне ұқсас болып келеді.
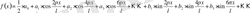 (7)
(7)
Мұндағы
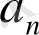 және
және
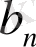 коэффициенттері келесі теңдіктермен анықталады:
коэффициенттері келесі теңдіктермен анықталады:
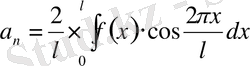 ,
,
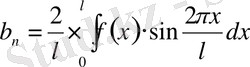 (8)
(8)
Егер
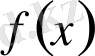 функциясы жұп функция болса, яғни
функциясы жұп функция болса, яғни
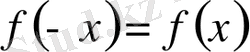 , онда
, онда
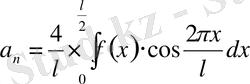 ;
;
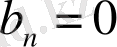 (9)
(9)
Егер
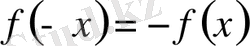 яғни
яғни
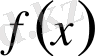 тақ функция болса, онда
тақ функция болса, онда
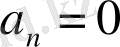 ,
,
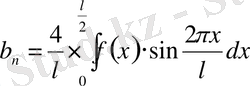 (10)
(10)
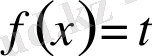 ,
,
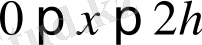 және
және
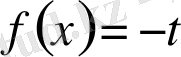 ,
,
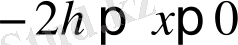 .
.
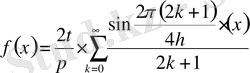 (11)
(11)
Егер
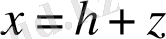 болса,
болса,
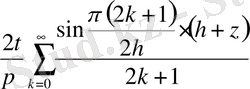 (12)
(12)
қатары
 аралығында
аралығында
 -ға тең болады.
-ға тең болады.
Осыдан
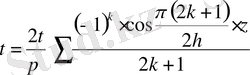 (13)
(13)
Егер (13) -теңдікті (6) -формуламен салыстыратын болсақ, онда
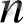 ,
,
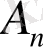 және
және
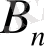 тұрақтыларға:
тұрақтыларға:
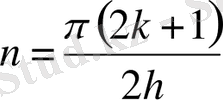 ,
,
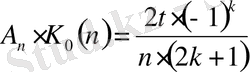 ,
,
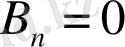 (14)
(14)
шамалар сәйкес келеді.
Осыдан
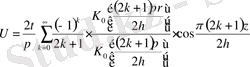 (15)
(15)
Егер (15) -формулада
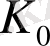 функциясын
функциясын
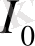 функциясына өзгертетін болсақ, онда бүйірлеріндегі температура
функциясына өзгертетін болсақ, онда бүйірлеріндегі температура
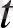 -ға, ал табандарындағы температура 0-ге тең болатын цилиндрдің ішіндегі температураның таралуы есебінің шешімі:
-ға, ал табандарындағы температура 0-ге тең болатын цилиндрдің ішіндегі температураның таралуы есебінің шешімі:
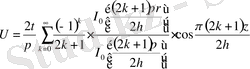 (16)
(16)
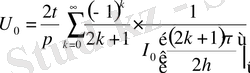 (17)
(17)
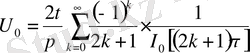 (18)
(18)
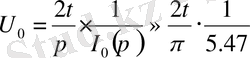
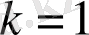 болғанда, онда
болғанда, онда
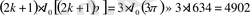 .
.
Бессель функциялары әйгілі неміс астрономы Фридрих Бессельдің құрметіне аталған. Ол күннің айналасындағы планеталардың қозғалысын зерттей отырып,
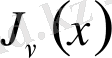 Бессель функциялары үшін рекуренттік қатынастарды қорытып шығарды,
Бессель функциялары үшін рекуренттік қатынастарды қорытып шығарды,
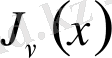 функцияның интегралдық көрінісін тапты және
функцияның интегралдық көрінісін тапты және
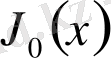 ,
,
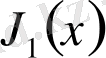 ,
,
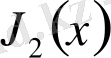 функциялары үшін алғашқы кестелерді құрды.
функциялары үшін алғашқы кестелерді құрды.
Алайда алғаш рет 1732 жылы
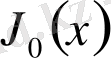 Бессель функцияларының бірі Даниил Бернулидің «Ауыр тізбектердің тербелісіне» арналған жұмысында қарастырылды. Д. Бернулли
Бессель функцияларының бірі Даниил Бернулидің «Ауыр тізбектердің тербелісіне» арналған жұмысында қарастырылды. Д. Бернулли
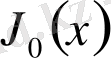 функциясының өрнегін дәрежелік қатар арқылы тапты және
функциясының өрнегін дәрежелік қатар арқылы тапты және
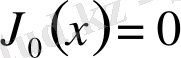 теңдеуінің сансыз көп түбірлері бар екенін байқады (дәлелдеусіз) .
теңдеуінің сансыз көп түбірлері бар екенін байқады (дәлелдеусіз) .
Сонымен қатар Бессель функциялары 1738 жылы жазылған Леонард Эйлердің «Дөңгелек мембрана тербелісін зерттеу» жұмысында кездеседі. Эйлер бұл жұмысында бүтін
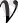 индексі үшін
индексі үшін
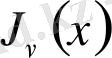 Бессель функциясының өрнегін
Бессель функциясының өрнегін
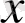 дәрежелік қатары арқылы тапты. Ал кейінгі жұмыстарында бұл өрнек
дәрежелік қатары арқылы тапты. Ал кейінгі жұмыстарында бұл өрнек
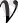 индексінің ерікті мәндеріне байланысты кеңейтілді.
индексінің ерікті мәндеріне байланысты кеңейтілді.
Кейбір зерттеушілер Бессель функцияларына қатысты негізгі нәтижелер және олардың математикалық физикада қолданылуы Л. Эйлердің атымен байланысты деп санайды.
ӘДЕБИЕТТЕР
- Грей Э., Мэтьюз Г. Б. Функция Бесселя и их применения в физике и механике, М., 1953.
- Зубов В. И. Функции Бесселя: Учебно-методическое пособие - М., 2007.
- Коренев Б. Г. Введение в теорию Бесселевых функций, «Наука», М., 1971.
- Кузьмин Р. О. Бесселевы функции, М., 1933.
- Қазақша-орысша, орысша-қазақша терминологиялық сөздік, «Рауан» баспасы, Алматы, 1999.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz