Кернеулі күй теориясы. Басты кернеулер мен басты жазықтықтар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

7-тәжірибелік сабақ

«Кернеулі күй теориясы. Басты кернеулер мен басты жазықтықтар»

Құрылым элементтерінің бір-біріне әсері, тік және жанама кернеулермен сипатталады. Олардың мәндері берілген нүкте арқылы жүргізілген қиманың бағытына байланысты.

Қарастырылатын нүкте арқылы жүргізілген барлық аудан-шалардағы кернеулер жиынтығы кернеулі күй деп аталады.

Жанама кернеулер нөлге тең ауданшалар, басты ауданшалар, осы ауданшалардағы тік кернеулер басты кернеулер деп аталады.

Басты кернеулер σ ₁ , σ ₂ , σ ₃ -әріптерімен белгіленеді. Созылған немесе сығылған сырық үшін 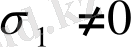_, σ ₂ =σ ₃ =0.

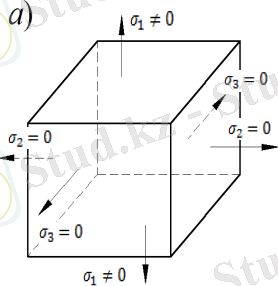
Екі басты кернеу нөлге тең болатын жағдай сызықтық кернеулі күй.

Кез-келген күштің әсеріндегі дене нүктесінің айналасынан, жанама кернеу нөлге тең болатындай өзара перпендикуляр үш ауданшаны көрсетуге болады. Бұл ауданшаларда тек басты кернеулер әсер етеді.

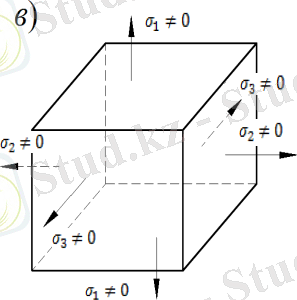
$Описание: C:\Users\Algazy\Desktop\11.png$ $Описание: C:\Users\Algazy\Desktop\11.png$ $Описание: C:\Users\Algazy\Desktop\11.png$

7. 1-сурет

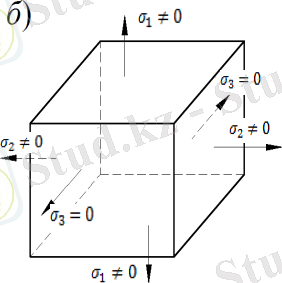
Сызықтық кернеулі күйде, екі басты кернеу нөлге тең (7. 1, а- сурет) . Үш басты ауданшаның біреуінде тік кернеу нөлге тең болса, жазық кернеулі күйді көрсетеді (7. 1, б-сурет) .

Басты кернеулердің ешқайсысы нөлге тең болмаса, кернеулі күй көлемдік кернеулі күй деп аталады (7. 1, в-сурет) .

Сызықтық, жазық кернеулі күйлерді көлемдік кернеулі күйдің жеке жағдайлары деп қарастыруға болады.

7. 1 Жазық кернеулі күй

Жазық кернеулі күйдегі денеден қалыңдығы бірге тең үшбұрышты призманы бөліп аламыз. Өзара перпендикуляр ас , аb ауданшаларға тік және жанама кернеулер әсер етеді. Нормалі x ауданшадағы кернеулер σ _x , τ _yх ; нормалі y ауданшадағы кернеулер σ _y , τ _xy , ал көлбеу жазықтықтағы кернеулер σ _α τ _α .

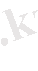
σ _x , σ _y , τ _xy , τ _yx мәндері белгілі, көлбеу жазықтықтағы кернеулерді анықтау керек. ( 7. 2, а-сурет) .

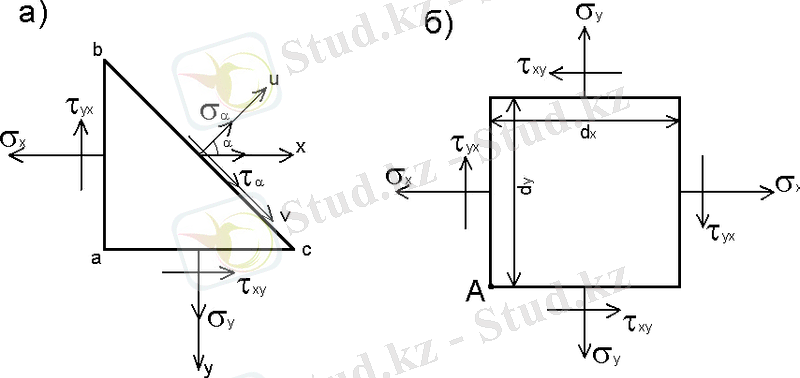
рис2-3

7. 2-сурет

Призмадан кесіп, алған өлшемдері dx, dy қалыңдығы бірге тең қарапайым элементті қарастырамыз (7. 2, б-сурет) . Элементтің өлшемдері өте аз болғандықтан, оның қарама-қарсы беттеріндегі кернеулер бірдей. Элементке әсер ететін барлық күштердің А нүктеге қатысты момент теңдеуі келесі түрде жазылады.

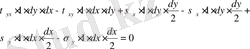
Теңдеуден τ _xy =τ _yx -жанама кернеулердің жұптылық заңы анықталады.

Үшбұрышты призманың тепе-теңдігін қарастырамыз (7. 2, а- сурет) . Көлбеу беттің ауданы А , онда қыр беттерінің аудандары A _ab =A cosα, A _ac =A sinα.

Барлық күштерді u бағытына проекцияласақ

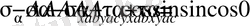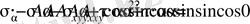Теңдеу ықшамдалғаннан соң

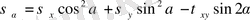(7. 1)

Күштердің υ бағыттағы проекциялары

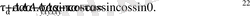
Өрнекті түрлендіргеннен соң

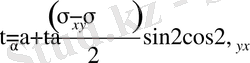(7. 2)

ескерсек.

(7. 1), (7. 2) өрнектері келесі түрде жазылады

(7. 3)

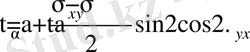(7. 4)

(7. 1), (7. 2), (7. 3), (7. 4) формулалары кез келген көлбеу жазықтықтағы тік және жанама кернеулерді анықтауға мүмкіндік береді.

Көлбеу cb жазықтығын басты ауданша ретінде қабылдасақ, онда бұл ауданшада жанама кернеу нөлге тең, яғни (7. 3) өрнегінен

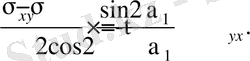(7. 5)

Немесе

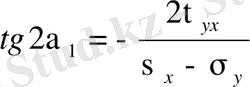(7. 6)

Тангенс функциясының периоды 180° болғандықтан, (7. 6) формуласынан бір-біріне перпендикуляр, екі басты ауданша анық-талады, олардың біреуі σ _x бағытымен, α бұрышын, ал екіншісі - 90°+α бұрышын жасайды. (7. 5) пен (7. 3) өрнектерінен

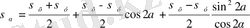
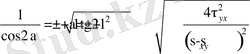ескерсек, онда басты кернеулер келесі түрде анықталады.

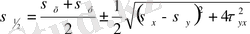(7. 7)

Түбірдің алдындағы плюс, минус таңбалары басты кернеулердің бірі св ауданшада, ал екіншісі оған перпендикуляр бағытта әсер ететіндігін көрсетеді. Егер x , y нормалі бар ауданшалар басты ауданшалар болып есептелінсе, онда σ _x =σ ₁ , σ _y =σ ₂ , τ _yx = τ _xy =0 (7. 1), (7. 2) формулаларынан басты кернеулер арқылы кез-келген ауданшадағы кернеулер анықталады.

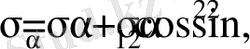(7. 8)

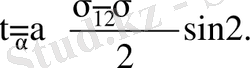(7. 9)

Айтылған ауданшаға перпендикуляр ауданшада

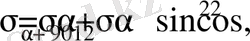(7. 10)

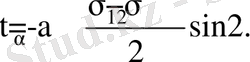(7. 11)

(7. 8), (7. 10) -ті қосатын болсақ

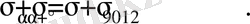(7. 12)

Яғни, өзара перпендикуляр ауданшалардағы тік кернеулердің қосындысы, басты кернеулердің қосындысына тең, тұрақты шама.

Жанама кернеудің ең үлкен мәні, басты кернеудің бағытымен 45° бұрыш жасайды, ал оның мәні

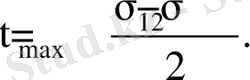(7. 13)

Басты кернеулер, тік кернеулердің ішінде ең үлкені немесе ең кішісі. Оны дәлелдеу үшін (7. 8) -тің бұрыш бойынша туындысын нөлге теңестіреді.

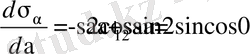
немесе

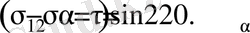
Жанама кернеу нөлге тең, ал бұл ауданшаларда тік кернеу ең үлкен және ең кіші мәнге ие болады.

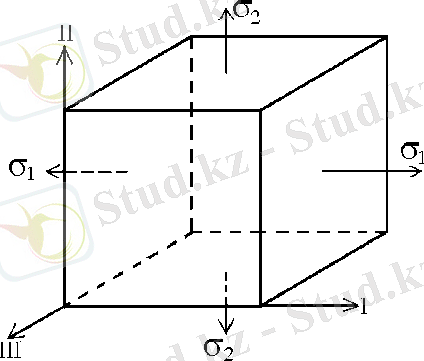
рис3-3

7. 3-сурет

Жоғарыдағы анықталған өрнектердің материалдар кедер-гісіндегі орны ерекше.

Кернеулер мен деформа-циялардың арасындағы байла-ныстарға тоқталайық. (3. 7. 3-су-ретте) көрсетілген элементтің беттерінде, σ ₁ , σ ₂ басты кер-неулер әсер етеді. Элементтің өстер бойымен ұзаруын анық-тайық.

7. 3-сурет:

Жоғарыдағы анықталған өрнектердің материалдар кедер-гісіндегі орны ерекше.Кернеулер мен деформа-циялардың арасындағы байла-ныстарға тоқталайық. (3. 7. 3-су-ретте) көрсетілген элементтің беттерінде, σ1, σ2басты кер-неулер әсер етеді. Элементтің өстер бойымен ұзаруын анық-тайық.:

Гук заңынан 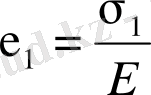, I бағыттағы ұзарудың әсерінен II , III бағыттарда элемент қысқарады, яғни

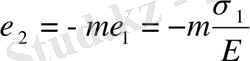
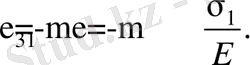
Дәл осылай, σ ₂ кернеуінің әсерінен

Сонымен, әрбір бағыттағы деформациялардың қосындысы

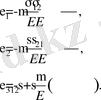(7. 14)

Егер, σ ₁ ≠0, σ ₂ =0 болса σ′ _x =σ ₁ cos ² α, σ _y ′=σ ₁ sin ² α немесе

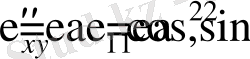
ал, σ ₁ =0 , σ ₂ ≠0 жағдайда σ _x ′′=σ ₂ sin ² α , σ _y ′′=σ ₂ cos ² α

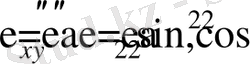
σ ₁ ≠0 , σ ₂ ≠0 болғанда

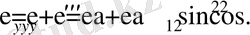
Осы өрнектерге (7. 14) пайдалансақ

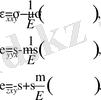(7. 15)

Сонымен, кернеулер мен деформациялардың арасындағы байланыстарды таптық. (7. 14) өрнегінен σ ₁ , σ ₂ анықтасақ, жазық кернеулі күй үшін Гуктың жалпылама заңы

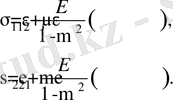(7. 16)