Статикалық анықталмаған жүйелер: күш әдісінің канонды теңдеулері, есептеу тәсілдері және M, Q, N эпюраларының тексерісі


Статикалық анықталмаған жүйелер
Жоспар:
1. Статикалық анықталмау.
2. Күш әдісінің канонды теңдеулері.
3. Статикалық анықталмаған жүйелерді есептеу.
4. Симетрияны пайдалану.
5. Көлденең және бойлық күштердің эпюраларын тұрғызу.
6. M, Q және N эпюраларының дұрыстығын тексеру.
1. Статикалық анықталмау
Кейбір сырықтар жүйесін есептегенде олардың бойындағы күштерді анықтауға статика теңдеулері жеткіліксіз, қосымша деформация теңдеулері қажет. Мұндай жүйелер, статикалық анықталмаған жүйелер деп аталады.
Статикалық анықталмаған жүйелердің ерекшеліктері: олардың бойындағы ішкі күштер сыртқы жүктемелермен қатар жеке элементтерінің көлденең қималарының арасындағы қатынасқа, және материалдарына байланысты серпімділік модуліне де тәуелді.
Статикалық анықталмаған жүйелерді есептеу, олардың есептеу нұсқаларын талдаудаудан, статикалық анықталмау дәре-жесін анықтаудан басталады.
Статикалық анықталмау дәрежесі - артық байланыстар саны-на тең, олардан босанғанда, жүйе статикалық анықталған, геомет-риялық өзгермейтін жүйеге айналады.
Статикалық анықталған жүйелерде ешқандай артық байланыс болмайды, олардың біреуінен босанғанның өзінде, жүйе геометриялық өзгермелі механизмге айналады.
1, а-суреттегі арқалық бір рет статикалық анықталмаған, себебі тірек байланыстарының біреуі артық. Байланыстардың біреуінен босатып (1, б, в-сурет) немесе қосымша топса енгізсе, жүйе статикалық анықталған, геометриялық өзгермейтін арқалыққа айналады.
Бірнеше элементтерден құралған тұйық тізбекті жүйе, тұйық контур деп аталады.
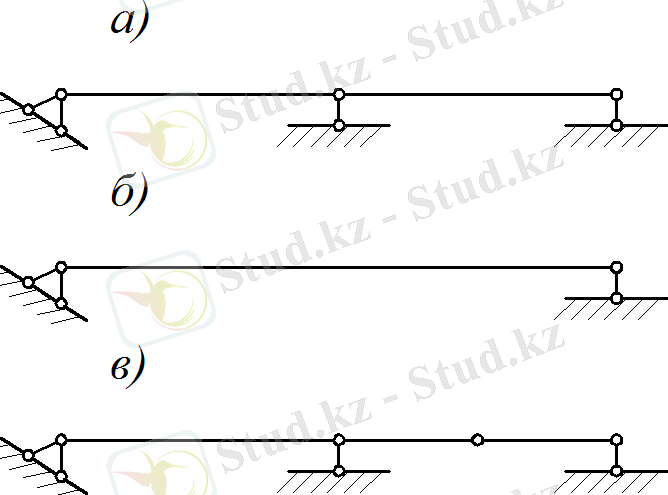
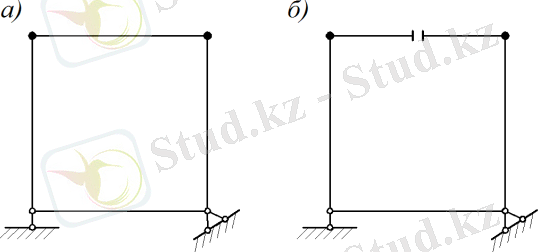
1-сурет 2-сурет
2, а суреттегі рама тұйық контур, үш рет статикалық анықталмаған. Элементтерінің бірін кессе, үш байланыстан босанып, статикалық анықталған жүйеге айналады. Бойлық күш, көлденең күш, ию моменті байланыстың реакциялары статика теңдеулерімен анықталмайды.
3 суреттегі рамалық жүйенің жоғарғы контурында топса орналасқан, екі рет статикалық анықталмаған, бұл контурды қиғанда, оған екі ішкі күш N , Q әсер етеді.
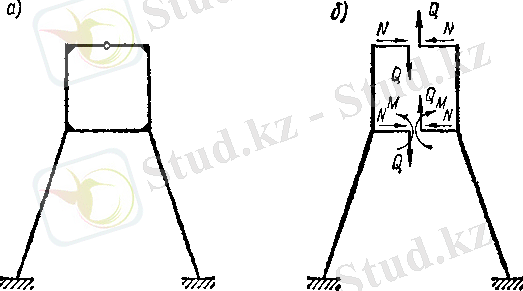
3-сурет
Бұл жүйенің, статикалық анықталмау дәрежесін өзге жолмен де анықтауға болады. Топсасы бар жоғарғы контур, екі рет статикалық анықталмаған. Әрбір қатаң бекітпеде үш тірек реакциясы бар, яғни төменгі контурда алты байланыс, статика теңдеулерінің саны үшеу, сондықтан үш байланыс артық. Сонымен жүйе бес рет статикалық анықталмаған.
Екі сырық қосылған түйінге, сырық өсінің кез-келген жерінде енгізілген топса жүйенің статикалық анықталмау дәрежесін бірге кемітеді. Мұндай топса жеке топса деп аталады.
Жүйені байланыстан босатқанда, құрылым геометриялық өзгермейтін болуы тиіс. 4, а суреттегі жүйе бір рет статикалық анықталмаған, оны тік орналасқан сырықтан босатса (4, б-сурет) қалған үш сырық раманың A нүктесіне қатысты айналуына кедергі бола алмайды (геометриялық өзгермелі жүйе) . Байланыстан дұрыс босанудың жолы 4, в-суретте көрсетілген.
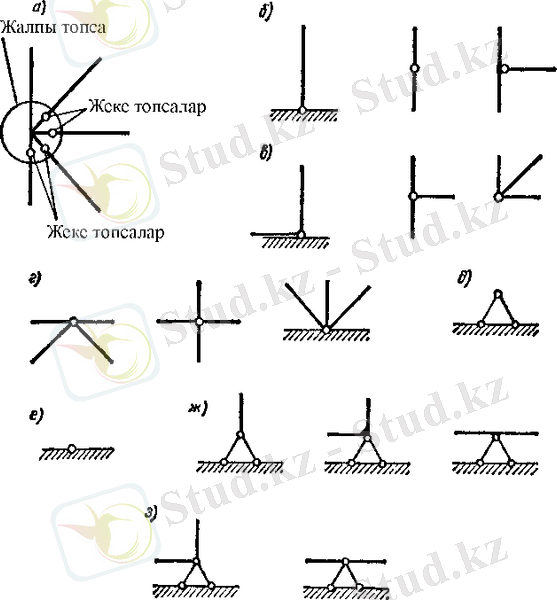
Жүйенің статикалық анықталмау дәрежесін анықтаудың жалпы түрін көрсетейік, k сырықты қосатын түйінге енгізілген топса, жүйенің статикалық анықталмау дәрежесін k -1-ге кемітеді, мұндай топса k -1 жеке топсаны алмастырады (5, а сурет) . Құрылымның статикалық анықталмау дәрежесін анықтау үшін тұйық контурды үш еселеп, (барлық топса, оның ішінде тірек, қатаң бекітпеден алмастырылады), оны енгізілген жеке топсалар санына кемітеді.
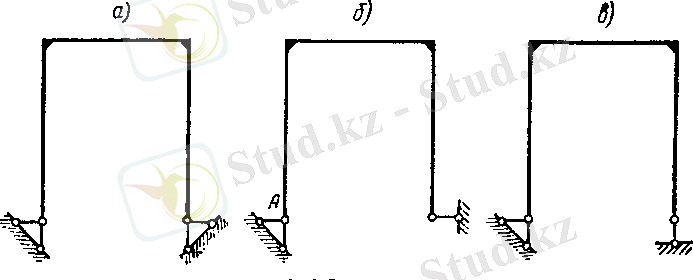
4-сурет
5-сурет
c =3 n - m , (1)
мұндағы с -статикалық анықталмау дәрежесі, n тұйық контур саны, m -жеке топсалар саны.
5, б суретте жеке, 5, в суретте қос, 5, г суретте үштік топсалар көрсетілген. Топсалы жылжымайтын тіректі (5, д-сурет) құрылымды, жермен байланыстыратын жеке топса түрінде көрсетуге болады (5, е-сурет) . Мұндай тірек құрылымды, жермен бір түзу немесе сынық элемент арқылы байланыстырса (5, ж- сурет), оны жеке, ал екі элемент арқылы байланыстырса (5, з- сурет) қос топсаға т. с. с жатады.
6-сурет
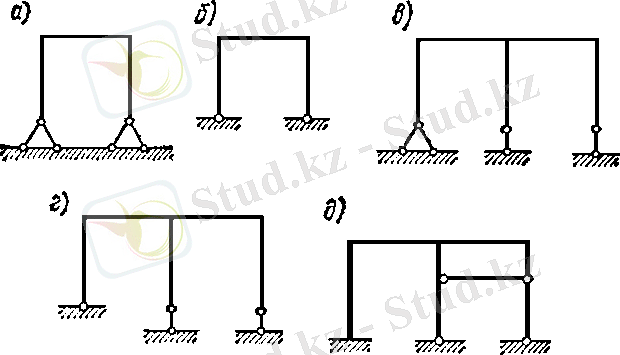
6, а суреттегі рама бір тұйық контурлы, екі топсалы деп қарастырылады, оның статикалық анықталмау дәрежесі
c =3⋅1-2=1
6, в, г суреттеріндегі рамалар екі тұйық контурлы, бес топсалы, статикалық анықталмау дәрежесі
c =3⋅2-5=1
6, д суреттегі рама үш тұйық контурлы, үш жеке, бір қос топсалы (оң жақтағы тік сырық ортасындағы топса), онда
c =3⋅3-3-2=4
Кез-келген статикалық анықталмаған жүйеден, оның геометриялық өзгермейтін күйін сақтайтындай бір байланыстан босануға болады, олар шартты қажетті байланыстар, бірақ, кейбір байланыстан босатқанда жүйе, геометриялық өзгермелі жүйеге өтеді (4, а суреттегі тік тірек сырықтары) . Мұндай байланыстар абсолютті қажетті деп саналады.
2. Күш әдісінің канонды теңдеулері
Статикалық анықталмаған жүйелердегі күштерді анықтау үшін, қосымша деформация теңдеулерінің қажеттілігі белгілі. Ол үшін, артық байланыстардан босанып, жүйені статикалық анық-талған негізгі жүйеге айналдырады. Алып тасталынған байла-ныстардың реакцияларына баламалы күштермен жүктегенде, жүйе бойындағы ішкі күштердің шамалары өзгермейді. Берілген күштер мен алынған байланыстардың реакцияларына тең күштердің әсерінен, негізгі жүйеде пайда болатын ішкі күштер, берілген жүйедегі ішкі күштерге тең, яғни екі жүйе бір-біріне баламалы.
Берілген жүйенің байланыс бағытындағы орын ауыстыруы болмайды. Сондықтан негізгі жүйеде алып тасталынған байланыс бағытындағы орын ауыстыруы нөлге тең. Сонымен, алынған байланыстардағы реакция, байланыс бағытындағы орын ауыстыру нөлге тең шартынан анықталады.
Күштердің бір-біріне тәуелсіз принципінен, кез-келген алынған байланыстың бағытындағы орын ауыстырудың нөлге теңдігінен:
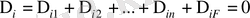 . (2)
. (2)
Қос индекстің біріншісі орын ауыстыру бағытын, екіншісі оның себебін білдіреді. ∆ ik , ∆ iF - сәйкесінше k реакциясы мен F күшінің әсерінен i реакциясы бағытындағы орын ауыстырулары.
Кез-келген k байланыстың реакциясы x k , ∆ ik орын ауысты-руын, ∆ ik =x k δ ik бірлік орын ауыстыруымен алмастырсақ (2. 13), келесі түрде жазылады.
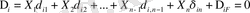
Сонымен, берілген және негізгі жүйелердің баламалығы, математика тілінде келесі теңдеулер жүйесін қанағаттандыруы тиіс.
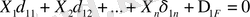
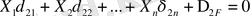
(3)
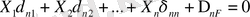
(3) теңдеулері, n рет статикалық анықталмаған жүйе үшін деформацияның қосымша, канонды теңдеулері деп аталады. Теңдеулердің әрбір қатары, сәйкес реакция бағытындағы орын ауыстыру нөлге тең екендігін білдіреді, олардың саны алып тасталынған байланыстар санына, яғни статикалық анықталмау дәрежесіне тең.
Теңдеулер жүйесінің δ ik коэффициенттері, i бағытындағы k бағытында әсер ететін бірлік күштің әсерінен, орын ауыстыруды білдіреді. Теңдеулердің индекстері бірдей δ ii басты, әртүрлі индексті δ ik бүйір элементтері деп аталады.
Орын ауыстырудың өзара қатысты теоремасы δ ik =δ ki канонды теңдеулердің коэффициенттерін анықтауды жеңілдетеді.
Канонды теңдеулердің коэффициенттерін анықтау үшін бірлік эпюралар
 мен күштік эпюра
M
F
тұрғызылады. Бірлік орын ауыстырулар
δ
ik
, бірлік
мен күштік эпюра
M
F
тұрғызылады. Бірлік орын ауыстырулар
δ
ik
, бірлік
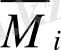 мен
мен
 эпюраларын, ал бос мүшелер
∆
ik
, бірлік
эпюраларын, ал бос мүшелер
∆
ik
, бірлік
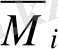 эпюралары мен күштік
M
F
эпюрасын көбейту негізінде табылады.
эпюралары мен күштік
M
F
эпюрасын көбейту негізінде табылады.
Басты элементтер тек оң таңбалы, бүйір элементтері мен күштік орын ауыстырулардың таңбалары оң, теріс және нөлге тең болуы мүмкін.
Барлық бірлік коэффициенттері мен бос мүшелері анықтал-ғаннан соң, канонды теңдеулерді шешіп, белгісіздерді анықтайды. Әрбір бірлік эпюраларды, сәйкес белгісіздердің X 1 , X 2 . . . , X n мәндеріне көбейтіп, түзетілген эпюралар тұрғызылады. Түзетілген эпюралар мен күштік эпюраның сәйкес ординаталарын қосып, берілген статикалық анықталмаған жүйенің, ию моментінің эпюрасын тұрғызады (соңғы эпюра) .
Ию моментінің соңғы эпюрасын басқа жолмен де тұрғызуға болады. Ол үшін, негізгі жүйені берілген және табылған күштермен жүктеп, белгілі әдіспен соңғы эпюраны тұрғызады.
Бір құрылымды есептеу үшін, әртүрлі негізгі жүйе қабылдау-ға болады, бірақ мүмкіндігінше бүйір элементтерінің көпшілігі нөлге тең, ал негізгі жүйе үшін, ию моментінің эпюралары қарапайым болатындай тиімдісін таңдаған жөн.
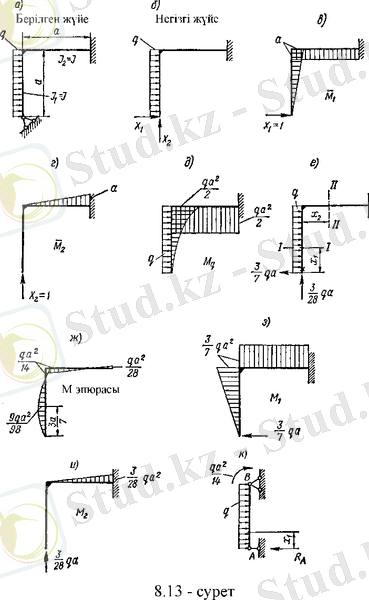
Үш рет статикалық анықталмаған раманы қарастырайық (7, а-сурет) .
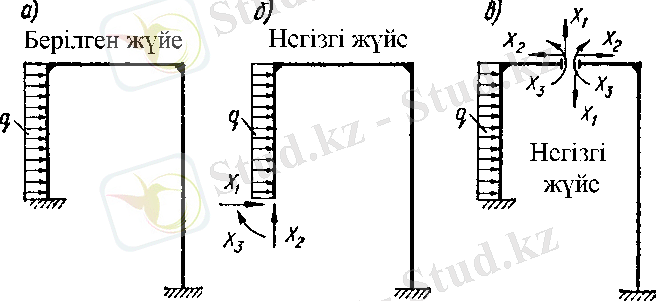
7-сурет
Раманы, сол тірегінің тік, горизонталь орын ауыстыруы мен бұрылуын шектейтін үш байланыстан босатса, негізгі жүйе 7, б суреттегідей түрде болады. Белгісіздер X 1 , X 2 , X 3 алып тасталған тіректердің реакцияларын, ал канонда теңдеулері белгісіз күштер бағытындағы орын ауыстырулар нөлге тең екендігін білдіреді.
Негізгі жүйе ретінде, 7, в суреттегі горизонталь элементі кесілген раманы қабылдауға болады. Мұндай кесудің негізінде, іргелес қималардың бір-біріне қатысты тік, горизонталь бағыттағы жылжуы мен бұралуы шектелуі тиіс, осыған орай белгісіздердің X 1 , X 2 , X 3 әрқайсысы жеке түрде емес, екі күштен және екі моменттен, яғни топталған белгісіздерден тұрады.
7, б суреттегі негізгі жүйедегі δ 12 раманың сол жақтағы ұшының X 2 = 1 күшінен горизонталь бағыттағы орын ауыстырудың, 7, в суреттегі негізгі жүйеде δ 12 , X 2 = 1 күшінің әсерінен іргелес қималардың бір-біріне қатысты тік бағыттағы орын ауыстыруын білдіреді.
Берілген 7, а суреттегі раманы есептеуде негізгі жүйе ретінде 7, в суретті қабылдаған тиімді, себебі күштік ию моментінің эпюрасы, тек раманың сол бөлігінде ғана, ал 7, б суреттегі негізгі жүйеде ию моментінің эпюрасы раманың барлық элементтерінде тұрғызылады.
3. Статикалық анықталмаған жүйелерді есептеу
Статикалық анықталмаған 8, а суреттегі раманы есептейік. Рама екі рет статикалық анықталмаған. Негізгі жүйе ретінде 8, б суреттегі сынық білеу қабылданады.
Жүйенің канонды теңдеулері:
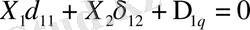 ,
,
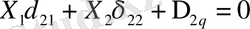
Негізгі жүйе үшін бірлік және күштік эпюралар 8, в, г, д суреттерде бейнеленген.
δ
11
анықтау үшін
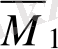 эпюрасын өзіне көбейтеміз (Верещагин әдісі) .
эпюрасын өзіне көбейтеміз (Верещагин әдісі) .
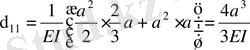 .
.
δ
12
, δ
21
анықтау үшін
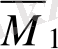 эпюрасы
эпюрасы
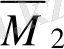 эпюрасына көбейтіліеді.
эпюрасына көбейтіліеді.
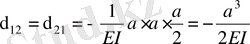 .
.
δ
22
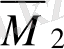 эпюрасын өзіне көбейту арқылы анықталады
эпюрасын өзіне көбейту арқылы анықталады
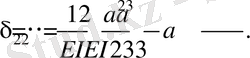
Бірлік
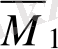 ,
,
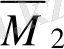 эпюраларын кезекпен
M
q
эпюрасына көбейтіп, бос мүшелерді анықтаймыз.
эпюраларын кезекпен
M
q
эпюрасына көбейтіп, бос мүшелерді анықтаймыз.
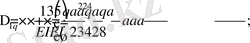
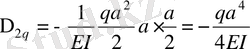 .
.
Табылған мәндерді канонды теңдеуге қойып, ортақ көбейткіш a 3 /EI -ге бөліп
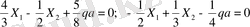 .
.
Теңдеулерді шешіп
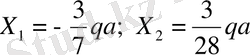 табамыз.
табамыз.
Ию моментінің соңғы эпюрасын тұрғызу үшін, негізгі жүйені берілген күш және табылған белгісіздермен жүктейміз. Теңдеуді шешкенде, X 1 таңбасы теріс болғандықтан, оны оңнан солға бағыттаймыз (8, е-сурет) .
Раманың әрбір аралығына ию моментінің теңдеуін жазамыз
I-I қима
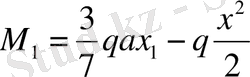
x
1
=0 болғанда M
1
=0;
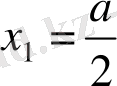 болғанда
болғанда
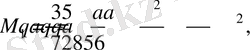
x
1
=
а
болғанда
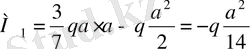
М 1мах анықтау үшін оның х бойынша бірінші туындысын нөлге теңестіреміз
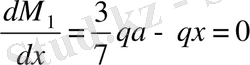 немесе
немесе
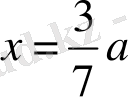 , онда
, онда
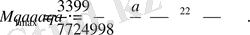
II-II қима
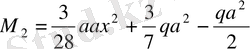 .
.
х
2
=0 болғанда
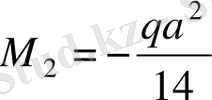 ;
х
2
=
а
болғанда
;
х
2
=
а
болғанда
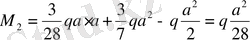 .
.
Ию моментінің соңғы эпюрасы 8, ж суретте көрсетілген.
Ию моментінің соңғы эпюрасын басқа әдіспен де тұрғызуға болады. Бірлік
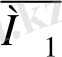 эпюрасының барлық ординатоларын
эпюрасының барлық ординатоларын
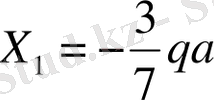 ,
,
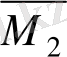 -ні
-ні
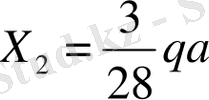 -ға көбейтіп 8, з, и суреттеріндегі түзетілген эпюралар
М
1
, М
2
алынады. Табылған
М
1
, М
2
және
М
q
эпюраларын қосып соңғы ию моментінің эпюрасын тұрғызады.
-ға көбейтіп 8, з, и суреттеріндегі түзетілген эпюралар
М
1
, М
2
алынады. Табылған
М
1
, М
2
және
М
q
эпюраларын қосып соңғы ию моментінің эпюрасын тұрғызады.
Раманың горизонталь элементінің қатаң бекітілген қимасында
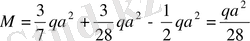 ;
;
сол жақтағы ұшында
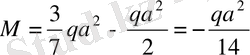 .
.
Рама қадағының, кез-келген қимасындағы ию моментін анықтау үшін, оны ұзына бойы таралған
q
күшімен және жоғарғы ұшында
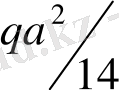 моментімен жүктелген қарапайым арқалық ретінде қарастырады (8, к-сурет) . Арқалықтың төменгі тірек реакциясы:
моментімен жүктелген қарапайым арқалық ретінде қарастырады (8, к-сурет) . Арқалықтың төменгі тірек реакциясы:
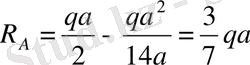 ,
,
х 1 қимасындағы ию моменті
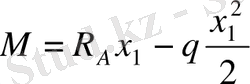 .
.
Табылған ординоталар бойынша, ию моментінің соңғы эпюрасы М тұрғызылады (8, ж-сурет) .
Қарастырылған мысалдың негізінде статикалық анықталмаған жүйелерді келесі тәртіппен есептеуге болады:
1. Берілген жүйені артық байланыстардан босатып негізгі жүйе қабылданады.
2. Алып тасталынған байланыстардың әсерін негізгі жүйеде белгісіз күштермен алмастырады.
3. Белгісіз және берілген күштердің әсерінен, белгісіз күш-тердің бағытында негізгі жүйеде орын ауыстыру нөлге тең екендігі ескеріліп, кононды теңдеулер құралады.
4. Негізгі жүйе жеке-жеке бірлік
X
1
=
1,
X
2
=1, …,
X
n
=1 күштері-мен жүктеліп, бірлік эпюралар
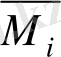 және берілген күштермен жүктеліп күштік эпюра
М
F
тұрғызылады.
және берілген күштермен жүктеліп күштік эпюра
М
F
тұрғызылады.
5. Бірлік эпюраларды бір-бірімен көбейтіп, канонды теңдеу-лердің коэффициенттері
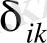 анықталады.
анықталады.
6. Бірлік эпюраларды кезекпен күштік эпюрамен көбейтіп, канонды теңдеулердің бос мүшелері
 анықталады.
анықталады.
7. Канонды теңдеулер жүйесін шешіп, белгісіз X 1 , X 2 , …X n та-былады.
8. Бірлік эпюралардың ординаталарын сәйкес табылған белгісіздердің мәндеріне көбейтіп, түзетілген эпюралар тұрғызылады. Түзетілген эпюралар мен күштік эпюраны қосып, ию моментінің соңғы эпюрасы тұрғызылады немесе табылған белгісіздер мен берілген күштер арқылы негізгі жүйені жүктеп, олардың әсерінен ию моментінің соңғы эпюрасын тұрғызады.
4. Симетрияны пайдалану
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz