Фалес теоремасы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Фалес теоремасы

1. Сыныпты екі топқа бөліп, бірінші топқа параллелограмм мен ромб, екінші топқа тіктөртбұрыш пен квадраттың ұқсастықтары мен айырмашылықтарын венн диаграммасында көрсетіп, қасиеттерін атау тапсырылады. Циркуль мен сызғыштың көмегімен салу есептерін өткенбіз. Циркуль мен сызғышты пайдаланып кесіндіні тең екі кесіндіге қалай бөлетін едік? Қалай салатынын тақтада бір оқушы көрсетеді.

Ал енді кесіндіні циркульмен сызғышты пайдаланып үш, төрт, бес т. б. кесінділерге қалай бөлуге болады? Бұл сұраққа жауап беру үшін ежелгі грек математигі Фалес теоремасын қолданады екенбіз.

3. Фалес теоремасы

а) Тарихына тоқталу

Фалес Милетский грек ғалымдарының тұңғышы б. э. д. 625-547 жылдар шамасында өмір сүрген. Бүгінгі өтетін теоремамыз кесіндіні циркуль мен сызғыштың көмегімен тең бөліктерге бөлуге қолданылады. Фалес диаметр дөңгелекті қақ бөлетінін, тең бүйірлі үшбұрыштың табанындағы бұрыштары тең болатынын, вертикаль бұрыштардың теңдігін, үшбұрыштардың теңдігінің бірінші белгісін алғаш дәлелдеген. Б. ж. с. бұрын 585 жылғы 28 майда болған күн тұтылу құбылысын алдын ала, алты ай бұрын айтқан. Гректер дүниеде жеті-ақ адам данышпан болып туады депойлаған, Фалес солардың біріншісі деп есептеген.

ә) Фалес теоремасы.

Егер бұрыштың қабырғаларын қиятын параллель түзулер оның бір қабырғасында тең кесінділер қиса, онда олар екінші қабырғасында да тең кесінділер қияды.

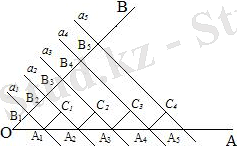Берілгені: <АОВ

а ₁ ІІ а ₂ ІІ а ₃ ІІ а ₄ ІІ а ₅ ІІ . . .

а ₁ ОА=A ₁ , а ₂ ОА=A ₂ …

а ₁ ОB=B ₁ , а ₂ ОB=B ₂ …

OA ₁ =A ₁ A ₂ =A ₂ A ₃ =…

Д/к: ОВ ₁ =B ₁ B ₂ =B ₂ B ₃ =…

Дәлелдеуі: A ₁ C ₁ II OB, A ₂ C ₂ II OB, A ₃ C ₃ II OB кесінділерін жүргіземіз.

Параллель түзулерді үшінші түзумен қиғандағы сәйкес бұрыштар болғандықтан < C ₁ A ₁ A ₂ = <C ₂ A ₂ A ₃ = <C ₃ A ₃ A ₄ және <С ₁ А ₂ А ₁ =<С ₂ A ₃ A ₂ =< C ₃ A ₄ A ₃

ал шарт бойынша A ₁ A ₂ =A ₂ A ₃ =A ₃ A ₄ онда үшбұрыштар бір қабырғасы және оған іргелес екі бұрышы сәйкесінше тең болғандықтан ΔA ₁ C ₁ A ₂ =ΔA ₂ C ₂ A ₃ , ал үшбұрыштардың теңдігінен А ₁ С ₁ =A ₂ C ₂ болады. Сонда A ₁ B ₁ B ₂ C ₁ ; A ₂ B ₂ B ₃ C ₂ параллелограмм болады. Яғни А ₁ С ₁ =B ₁ B ₂ , A ₂ C ₂ =B ₂ B ₃ немесе В ₁ В ₂ =B ₂ B ₃

Қалған кесінділердің теңдігі де осылай дәлелденеді.

Ескерту: Бұрыштың қабырғаларының орнына кез келген екі түзуді алуға да болады. Теореманың қорытындысы сол күйінде қала береді. Берілген екі түзуді қиып өтетін және бір түзуден тең кесінділер қиып түсіретін параллель түзулер екінші түзуден де тең кесінділер қиып түседі.

4 . Фалес теоремасын практикада қолдануға есеп.

Есеп берілген АВ кесіндісін тең n белгілерге болу керек.

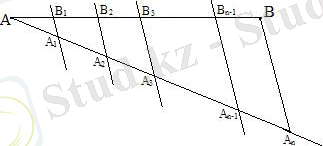Шешуі:

1) АВ кесіндісін қамтитын түзуде жатпайтын А нүктесінен бастап а сәулесін салам.

2) а сәулесінің бойына өзара тең АА ₁ , А ₁ А ₂ , А ₂ А ₃ , …, А _n-1 A _n кесінділерін өлшеп саламыз.

3) А _n B қосамыз

4) А ₁ В ₁ ІІ А ₂ В ₂ ІІ А ₃ В ₃ ІІ A _n В _n түзулерін жүргіземіз

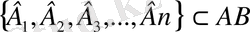Фалес теоремасы бойынша АB ₁ =B ₁ B ₂ =B ₂ B ₃ =…=B _n-1 B

«Фалес» сөзжұмбағын шешу»

Сұрақтары:

1. Геометрия - ол геометриялық . . . - лардың қасиеттері жөніндегі ғылым

2. Үшбұрыштың төбесін қарсы жатқан қабырғаның ортасымен қосатын кесінді?

3. Барлық қабырғалары тең үшбұрыш?

4. Бұрышты қақ бөлетін сәуле?

5. Бұрышты өлшейтін құрал?

Ф: Ф

Ф:

: А

Ф:

: Е

Ф:

: С

2. Тұрмыста кейбір шамалардың (ұзындықтың, массаның, температураның) өзгерістерінің сан мәні ғана жазылады.

Модуль латынша modulus - қазақша «мөлшер» деген мағынаны білдіреді. Кейбір жағдайда «модульдің» орнына абсолюттік шама деп те атайды.

Санның модулі дегеніміз координаталық түзудегі санды кескіндейтін нүктенің санақ басынан (бірлік кесінді есебімен алынған) қашықтығы.

Ара қашықтығы оң санмен немесе нөл санымен жазылатыны белгілі. Онда санның модулі координаталық түзуде берілген санды кескіндейтін нүктенің санақ басынан қашықтығы болғандықтан, модуль теріс санмен жазылмайды.

Координаталық түзуде 0 санын кескіндейтін нүкте санақ басымен беттеседі. Онда І0І = 0.

Нөл санының модулі 0-ге тең.

Теріс санның модулі оған қарам қарсы санға тең.

Оң санның модулі сол санның өзіне тең.

Тұрмыста кейбір шамалардың (ұзындықтың, массаның, температураның) өзгерістерінің сан мәні ғана жазылады.

Координаталық түзу бойынан А (-3) нүктесін белгілеп, А нүктесінің санақ басынан бірлік кесінді есебімен қашықтығын анықтайық. Координаталық түзу бойынан А (-3) нүктесі санақ басынан - О нүктесінен 3 бірлік кесіге тең қашықтықта жатыр.

Сонда, -3 санынң модулі 3-ке тең.

Оқылуы: "- 3 санынң модулі 3 - ке тең.

I. Теріс санның модулі оған қарам қарсы санға тең.

II. Оң санның модулі.

Мысалы, 3, 5 санының модулін табайық. Ол үшін координаталық түзу бойынан В (3, 5) нүктесін белгілейік. Координаталық түзу бойындағы В(5) нүктесінің санақ басынан қашықтығы 5 бірлік кесіндіге тең. Демек, 3, 5 санының модулі 3, 5 ке тең.

Оң санның модулі сол санның өзіне тең.

III. Нөл санының модулі 0-ге тең.

IV. Қарама - қарсы сандардың модульдері тең.

Енді модульмен берілген қарапайым теңдеулерді қарастырайық.

1) x=3, 2 болса, онда x=3, 2 және x=- 3, 2 болады.

2) x+2, 1=3, 6 x=3, 6 - 2, 1 x=1, 5 бұдан x=1, 5 және x=- 1, 5 шығады.

3. Дәреженің анықтамасын берместен бұрын, мынадай мысалдар қарастырайық.

1) 3+3+3+3=3*4=12, өйткені 3 саны төрт рет қосылған. Мұнда қосу амалы көбейту амалымен алмастырылған. Демек, бірнеше бірдей қосылғыштардың қосындысын бір қосылғыштың қосылғыштар санына көбейтумен алмастыруға болады.

2) Тура осылай бірнеше бірдей көбейткіштердің көбейтіндісін табуға болады. Мысалы, 3 санын өз-өзіне 4 рет көбейту үшін (3*3*3*3=81), қысқаша, яғни 3*3*3*3

= 34 түрінде жазылатын амалмен алмастыруға болады. Мұнда 34жазуы «3-тің төртінші дәрежесі»деп оқылады.

Осылай белгілеу арқылы кез келген бірдей көбейткіштердің көбейтіндісін табуға болады. 5*5*5=125; 7*7*7=343.

Жалпы түрде: а*а*а* . . . *а=аn.

Анықтама: Бірдей көбейткіштерден тұратын көбейтіндіні дәреже деп атайды. 3*3*3*3=34=81 теңдігіндегі 81 саны 3 санының төртінші дәрежесі. 34=81 жазуындағы 3 саны (қайталанатын көрсеткіш) дәреженің негізі, 4 саны дәреженің көрсеткіші, ал 81 саны 34 дәрежесінің мәні деп аталады.

аn өрнегіндегі а (қайталанатын көбейткіш) - дәреженің негізі, n(көбейткіштің неше рет қайталанатынын көрсететін сан(-дәреженің көрсеткіші деп аталады.

Дәрежені оқу кезінде алдымен оның негізі, содан кейін оның көрсеткіші оқылады. Мысалы, 34 өрнегі: «3 санының төртінші дәрежесі» немесе «3-тің төртінші дәрежесі» деп оқылады.

Санның 2-ші және 3-ші дәрежелері сәйкесінше «санның квадраты» және «санның кубы» деп аталады. Сонымен қатар келесі тұжырымдамаларды есте сақтау қажет:

3) а1=а, яғни кез келген санның бірінші дәрежесі өзіне тең.

Мысалы: 251=25, 1001= 100, 451=45

4) 10, 100, 1000, . . . разряд бірліктерін 10 санының дәрежесі түрінде жазуға болады.

Мысалы: 100=10⋅10=102

5) Санды өрнектің құрамында санның дәрежесі болса, онда дәрежеге шығаруды басқа амалдардан бұрын орындау керек.

Мысалы:152-100=15⋅15-100=225-100=125

Ү. Жаңа тақырыпты бекіту.

А) Оқулықпен жұмыс: деңгейлік тапсырмаларды орындау

А деңгейі:№290, 293, 296, 301

В деңгейі:№305

С деңгейі:№312

Ә) Топтық жұмыс: «Қатені тап»,

І топ 23 +10=2⋅3+10=16

18:32=6 2=6⋅6=36

ІІ топ 22 +72 = 92 =9⋅9=81

5 ⋅22 = 102 =10⋅10=100

Б) «Сәйкестендіру»

№ Тапсырма № Жауабы

1 5+5+5+5 1 54

2 6 ∙ 6 ∙ 6 2 5∙4

3 5 ∙ 5 ∙ 5 ∙ 5 3 63

4 7+7+7+7+7 4 7 ∙ 5

5 6+6+6 5 75

6 7 ∙ 7 ∙ 7 ∙ 7 ∙ 7 6 6 ∙ 3

В) топ басшылар сайысы:

1) у⋅у+1=82

2) 100-х⋅х=36

3) 2х⋅3х⋅5х=900

4) 2х⋅5х⋅11х=12100

ҮІ. Сергіту сәті. Сен білесің бе?

х 5 15 25 35 45

х2 25 225 625 1225 2025

х 55 65 75 85 95

х2 3025 4225 5625 7225 9025

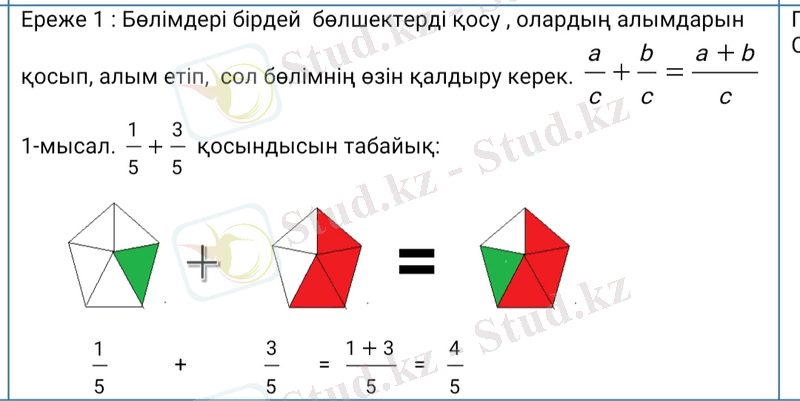
5. Трапеция деп екі қарама-қарсы қабырғасы параллель, ал басқа екі қабырғасы параллель емес төртбұрышты айтады.

Трапецияның параллель қабырғалары оның табандары, ал параллель емес қабырғалары - бүйір қабырғалары.

Трапецияның биіктігі деп табандарының ортақ перпендикулярын айтады, яғни бір табанының нүктесінен екінші табаны жататын түзуге жүргізілген перпендикуляр.

Трапецияның қасиеттері:

1-қасиет. Трапеция дөңес төртбұрыш болады.

2-қасиет. Трапецияның бүйір қабырғасына іргелес жатқан бұрыштарының қосындысы 180°-қа тең.

Теңбүйірлі және тікбұрышты трапецияның анықтамаларына тоқталу.

Теңбүйірлі трапецияның қасиеттері:

1. Теңбүйірлі трапецияның әр табандарына іргелес жатқан бұрыштары өзара тең болады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.