Девиссон - Джермер тәжірибелері мен Резерфордтың α-бөлшектер шашырау формуласы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Девиссон және Джермер тәжірибелері.

1927 жылы бөлшектердің толқындық табиғатын растайтын алғашқы эксперименттік зерттеулерді американдық физиктер к. Девиссон мен Л. Джермер жүргізді.

Бұл тәжірибенің идеясы, егер электронды сәулелер толқындық қасиетке ие болса, онда олардың кристалдан шағылысуы рентген сәулелері сияқты интерференциялық сипатта болуы керек, яғни осы кезде кристалдан рентген сәулелерінің шағылысуына ұқсас интерференциялық шағылысудың максимумдары байқалуы керек. Бұл кезде кристалдардың әртүрлі жазықтықтарынан атомдардан құлаған сәуленің дифракциясы нәтижесінде толқын осы жазықтықтардан шағылысқандай шығады.

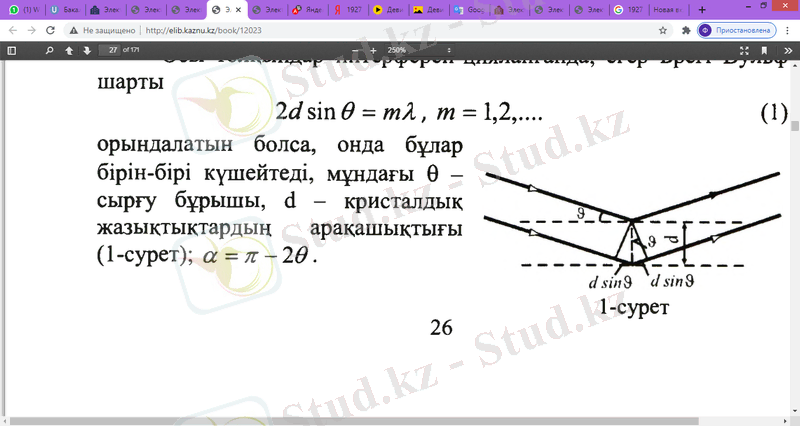
Осы толқындар интерференцияланан кезде, егер Брегг $-$ Вульф шарты орындалса,

$\mathbf{2d}\mathbf{\sin}\mathbf{\theta = m\lambda, \ \ \ \ \ m = 1, 2, \ldots}$

бұлар бір-бірін күшейтеді.

Мұндағы : $\mathbf{\theta} -$ сырғу бұрышы

$\mathbf{d} -$ кристалдық жазықтықтардың арақашықтығы(1 $-$ сурет)

$\mathbf{\alpha = \pi - 2\theta}$

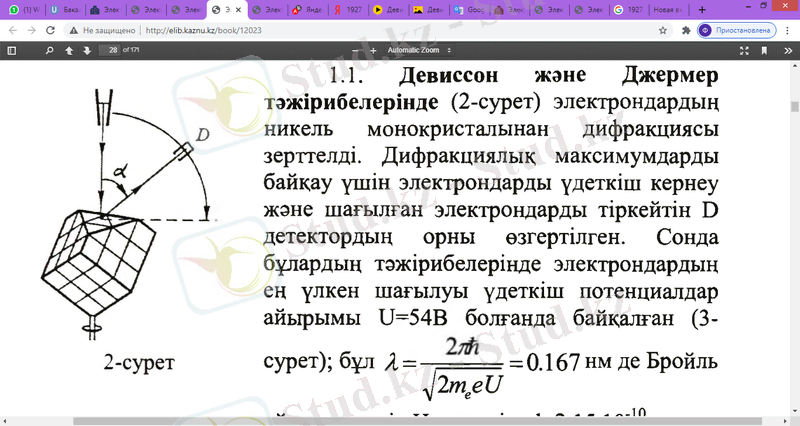
Девиссон және Джермер тәжірибелерінде (2 $-$ сур. ) никель монокристалынан электрондардың дифракциясы зерттелді. Дифракциялық максимумдарды бақылау үшін электрондарды үдеткіш кернеу мен шағылған электрондарды тіркейтін D детекторының орнын өзгертті. Сол тәжірибеле-

рінде электрондардың ең үлкен шағылуы үдеткіш потенциялдар айырымы U=54 B болғанда байқалған .

$\mathbf{\lambda =}\frac{\mathbf{2\pi\hslash}}{\sqrt{\mathbf{2}\mathbf{m}_{\mathbf{e}}\mathbf{eU}}}\mathbf{= 0. 167}$ нм

Бұл де Бройль толқын ұзындығына сәйкес келеді (3 $-$ сур. ) . Никельдің d=2, 15 $\bullet 10^{- 10}$ м тор тұрақтысы үшін Брэгг - Вульф шартынан анықталған толқын ұзындығы $\lambda = 0, 165$ нм болған. Осы эксперименттік және есептелінген $\lambda$ мәндердің дәлдігі Бройльдің бөлшектердің толқындық қасиеттері туралы гипотезасын керемет растайды.

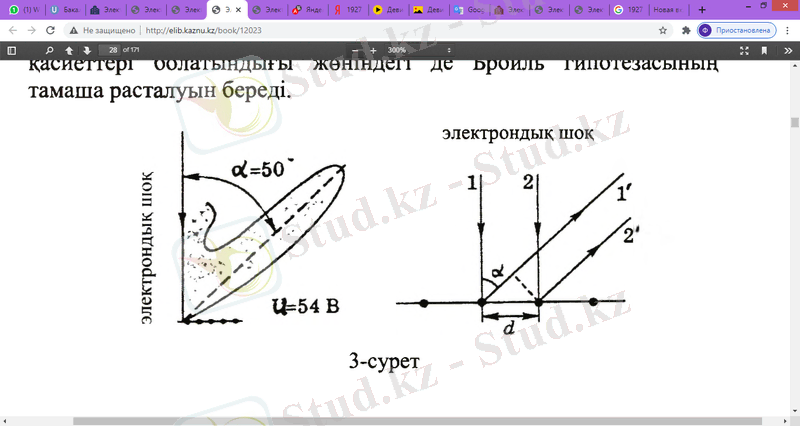
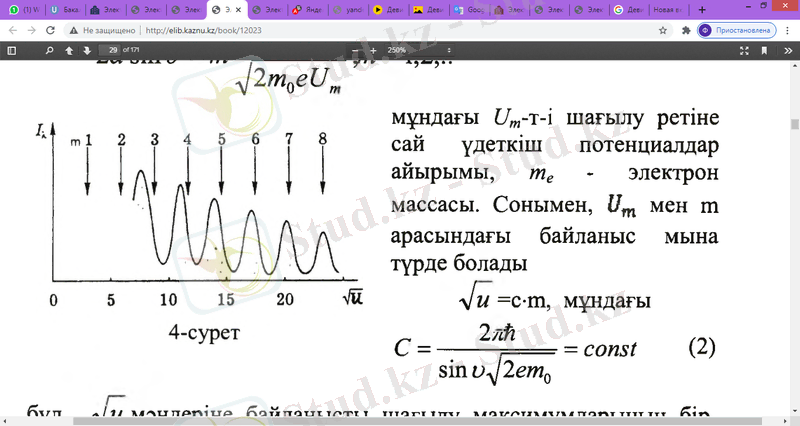
Девиссон мен Джермердің басқа тәжірибелерінде $\mathbf{\theta}$ тұрақты ( $\mathbf{\theta = const) }$ сырғу бұрышын қабылдай отырып, I шағылысқан электронды (4-сур) сәуленің интенсивтілігін U үдеткіш кернеуінің әртүрлі мәндерінде өлшеді. Экспериментте байқалатын шағылу максимумдары бір-бірінен $\sqrt{\mathbf{u}}$ мәні бойынша бірдей қашықтықта орналасады, бұл теорияда да расталады.

$\lambda\mathbf{=}\frac{\mathbf{2\pi\hslash}}{\sqrt{\mathbf{2}\mathbf{m}_{\mathbf{0}}\mathbf{K}}}\mathbf{=}\frac{\mathbf{2\mu\hslash}}{\sqrt{\mathbf{2}\mathbf{m}_{\mathbf{0}}\mathbf{eU}}}$

Брегг- Вульф шартынан мынаны аламыз

$\mathbf{2d}\mathbf{\sin}{\mathbf{\theta = m}\frac{\mathbf{2\pi\hslash}}{\sqrt{\mathbf{2}\mathbf{m}_{\mathbf{0}}\mathbf{e}\mathbf{U}_{\mathbf{m\mathbf{, \ \ m = 1, 2, . . }$

Mұндағы $\mathbf{U}_{\mathbf{m}}$ - ті шағылысуға сәйкес келетін үдеткіш потенциалдар айырмасы, $\mathbf{m}_{\mathbf{e}}$ - электрон массасы . Осылайша, $\mathbf{U}_{\mathbf{m}}$ мен $\mathbf{m}$ арасындағы байланыс келесідей болады.

$\ \sqrt{\mathbf{U}}\mathbf{= c \bullet m\ }$

мұндағы

$\mathbf{C =}\frac{\mathbf{2\pi\hslash}}{\mathbf{\sin}{\mathbf{v}\sqrt{\mathbf{2}\mathbf{e}\mathbf{m}_{\mathbf{0\mathbf{= const}$

Бұл $\sqrt{\mathbf{u}}$ мәндерімен байланысты шағылысу максимумы бір-бірінен бірдей қашықтықта болатындығын көрсетеді.

Дэвиссон мен Джермердің эксперименттерінің нәтижелері электрондардың толқындық табиғатын түсіндірді және де Бройль формулаларының дәлдігінің сандық дәлелі болды.

Резерфорд формуласын қорыту

Қaндай да бір зaттан α-бөлшектердің шашырау теориясын Э. Рутерфорд жасады. Ол θ бұрыш мәндеріне шашыраңқы α-бөлшектердің таралуын бейнелейтін формуланы қорытып шығарды.

α-бөлшегі бар атом ядросы арасындағы кулондық электростатикалық импульстің күші гиперболада қозғалса, α-бөлшектің θ бұрышының мәні оның бастапқы жылдамдығына, массасы m, заряды 2e және α-бөлшек ядроға жақын орналасқан p қашықтығына байланысты болады

$\mathbf{ctg}\frac{\mathbf{\theta}}{\mathbf{2}}\mathbf{=}\frac{\mathbf{4\pi}\mathbf{\varepsilon}_{\mathbf{0}}\mathbf{M}\mathbf{v}^{\mathbf{2}}\mathbf{p}}{\mathbf{z}\mathbf{z}_{\mathbf{1}}\mathbf{e}^{\mathbf{2}}}$

$(\theta, \theta + d\theta)$ сфералық белдеуде шашыраған DN бөлшектерінің санын анықтай отырып, сфералық белдеуге сәйкес келетін бұрыш d Ω тең

$\mathbf{dN = 2\pi nNpdp}$

$\mathbf{d\Omega = 2\pi\sin\theta d\theta}$ (1)

Дөңгелек сақинаның ауданы :

$\mathbf{S = 2\pi pdp}$

dσ үшін бөлшектің шашырауын сипаттайтын тиімді қима:

$\mathbf{d\sigma =}\frac{\mathbf{dN}}{\mathbf{N}}\mathbf{= 2\pi npdp}$ (2)

Осыдан pdp шамасы:

$\mathbf{pdp =}\frac{\mathbf{1}}{\mathbf{2}}\left( \frac{\mathbf{Z}_{\mathbf{1}}\mathbf{Z}\mathbf{e}^{\mathbf{2}}}{\mathbf{4\pi}\mathbf{\varepsilon}_{\mathbf{0}}\mathbf{M}\mathbf{v}^{\mathbf{2}}} \right) ^{\mathbf{2}}\frac{\mathbf{ctg}\frac{\mathbf{\theta}}{\mathbf{2}}\mathbf{d\theta}}{{\mathbf{s}\mathbf{in}}^{\mathbf{2}}\frac{\mathbf{\theta}}{\mathbf{2}}}$ (3)

Осы (3) өрнекті және (1) және (2) өрнектен анықталған формулаға қойғанда шығады:

(1) -ден : $\mathbf{2\pi =}\frac{\mathbf{d\Omega}}{\mathbf{\sin\theta d\theta}}$

(2) -ге: $\mathbf{\ d\sigma =}\frac{\mathbf{dN}}{\mathbf{N}}\mathbf{=}\frac{\mathbf{d\Omega}}{\mathbf{\sin\theta d\theta}}\mathbf{\bullet n \bullet}\frac{\mathbf{1}}{\mathbf{2}}\left( \frac{\mathbf{Z}_{\mathbf{1}}\mathbf{Z}\mathbf{e}^{\mathbf{2}}}{\mathbf{4\pi}\mathbf{\varepsilon}_{\mathbf{0}}\mathbf{M}\mathbf{v}^{\mathbf{2}}} \right) ^{\mathbf{2}}\frac{\mathbf{ctg}\frac{\mathbf{\theta}}{\mathbf{2}}\mathbf{d\theta}}{{\mathbf{s}\mathbf{in}}^{\mathbf{2}}\frac{\mathbf{\theta}}{\mathbf{2}}}\mathbf{=}\frac{\mathbf{n}}{\mathbf{2}}\mathbf{\bullet}\left( \frac{\mathbf{Z}_{\mathbf{1}}\mathbf{Z}\mathbf{e}^{\mathbf{2}}}{\mathbf{4\pi}\mathbf{\varepsilon}_{\mathbf{0}}\mathbf{M}\mathbf{v}^{\mathbf{2}}} \right) ^{\mathbf{2}}\mathbf{\bullet}\frac{\mathbf{d\Omega}}{{\mathbf{s}\mathbf{in}}^{\mathbf{2}}\frac{\mathbf{\theta}}{\mathbf{2}}}\mathbf{\bullet}\frac{\mathbf{ctg}\frac{\mathbf{\theta}}{\mathbf{2}}\mathbf{d\theta}}{\mathbf{\sin\theta d\theta}}$