Трапецияның орта сызықтарын зеттеу, қасиеттерін анықтау және оларды емтихан есептерін шығаруда қолдану

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Кіріспе

Ғылыми жобаның өзектілігі: 9 және 11 сыныптарда математика пәні бойынша емтихандарда Трапеция тақырыбында есептер көп кездеседі. Бұл тақырыпты 8 сыныпта өттік, бірақ оқулықта бұл тақырыпқа материалдар толық көрсетілмеген. Есептер шығару барысында көптеген қиындықтар туындады. Сондықтан Трапеция туралы қосымша мәліметтер жинақтауды бастадым. Ақпарат өте аз болды. Бірақ ақпарат жинау барысында Трапецияның екінші орта сызығы атты қызықты мақала тауып алдым (Кушнир И.А., Математика в школе №2, 1993ж). Кейін тағы да Трапецияның үшінші орта сызығы туралы мәлімет таптым. Менің сыныптастарым да трапецияның екінші және үшінші орта сызықтары туралы білмейтіндігі таң қалдырды. Сол кезде мен осы жұмбақ сызықтар туралы мәліметтер және оларға байланысты есептер жинақтап, өз жұмысды ғылыми жоба түрінде рәсімдеуді шешетім. Мен өз жұмысымды интернеттен, кітапханалардан, мұрағаттардан және математикалық анықтамалардан ақпарат жинаудан бастадым. Орта сызықтардың анықтамалары мен қасиеттерін анықтағаннан кейін есептер шығарудан қиналмайтын болдым. Менің ойымша, бұл жұмысты осы тақырыпта есептер шығаруда қиналатын оқушылар, емтиханға дайындық құралы ретінде қолдануға және геометрия пәніне деген қызығушылығы бар оқушыларға пайдалануға болады.

Ғылыми жобаның мақсаты: трапецияның орта сызықтарын зеттеу, қасиеттерін анықтау және оларды емтихан есептерін шығаруда қолдану.
Ғылыми жобаның міндеттері:
* негізігі ұғымдар мен анықтамаларды, тұжырымдар мен формулаларды жинақтау;
* жинақталған материалдарға шолу жасау,талдау;
* трапецияның орта сызықтары туралы мәліметтер жинақтау;
* трапецияның орта сызықтарының қасиеттерін зерттеу;
* трапецияның орта сызықтарына берілген есептерді шығару;
Ғылыми жобаның маңызы: жобада көрсетілген тапсырмалар оқушылардың жалпы оқу дағдыларының қалыптасуының базасы ретінде қызмет етеді. Бұл жоба материалдарын оқушылар олимпиадаға дайындалуына, сынақты сәтті тапсыруға және кейінгі жоғарғы оқу орындарында да көмекші құрал ретінде қолдануына болады.

1.Трапеция. Трапецияның орта сызықтары
1.1. Трапеция

Трапеция (грекше сөзбе - сөз - үстел ) - екі қабырғасы параллель, өзге екеуі параллель емес дөңес төртбұрыш. Параллель қабырғалары трапецияның табандары, ал параллель емес қабырғалары оның бүйір қабырғалары деп аталады.
Трапецияның төбесінен оған қарсы жатқан табанына немесе табанының созындысына түсірілген перпендикуляр оның биіктігі деп аталады (1 - сурет).

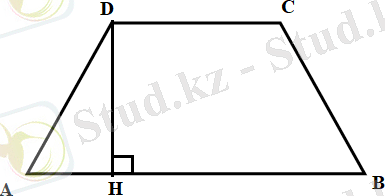
1 - сурет
Трапецияның бүйір қабырғалары тең болса, ол теңбүйірлі трапеция деп аталады (2,а - сурет) .
Трапецияның бір бұрышы тік болса, ол тікбұрышты трапеция деп аталады (2,ә - сурет).

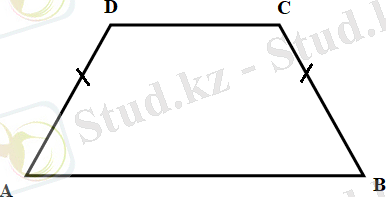
а) ә)
2 - сурет
1 - қасиет. Теңбүйірлі трапецияның табанындағы бұрыштары тең болады.
Дәлелдеуді. ABCD - теңбүйірлі трапеция, CD оның кіші табаны болсын (3,а - сурет ). АВ табанындағы бұрыштары тең болатынын дәлелдейік.
Трапецияның CF және DE биіктіктерін жүргіземіз. ADE және BCF тікбұрышты үшбұрыштары гипотенузасы мен катеті бойынша тең ( AD=BC, DE=CF ). Демек, А және В бұрыштары тең болады.
А және D,B және C бұрыштарының қосындысы 180° болғандықтан, А және В бұрыштарының теңдігінен D және C бұрыштарының теңдігі шығады. ∎
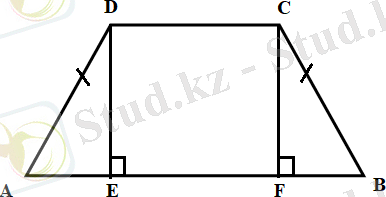
а) ә)
3 - сурет
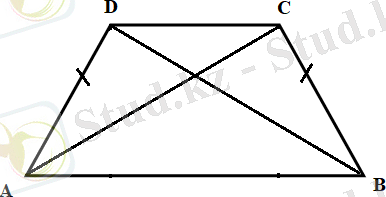
2 - қасиет. Теңбүйірлі трапецияның диагональдары тең болады.
Дәлелдеуі. ABCD - теңбүйірлі трапеция ( AB CD ), AC, BD оның диагональдары болсын (3,ә - сурет). Үшбұрыштардың теңдігінің бірінші белгісі бойынша ( АВ - ортақ қабырғасы, BC = AD, ABC=BAD ) ABC және BAD үшбұрыштары тең болады. Демек, AC= BD. ∎

1.2. Трапецияның бірінші орта сызығы

Трапецияның орта сызығы деп оның бүйір қабырғаларының орталарын қосатын кесіндіні айтады ( 4,а - сурет).
Теорема. Трапецияның орта сызығы табандарына параллель және олардың қосындысының жартысына тең.
Дәлелдеуі. ABCD трапециясын ( AB CD ) қарастырайық. EF кесіндісі - оның сәйкесінше AD және ВС бүйір қабырғаларының орталарын қосатын орта сызығы болсын. DF түзуін жүргіземіз және оның АВ түзуімен қиылысу нүктесін G арқылы белгілейік (4,ә - сурет).

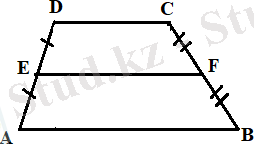
а) ә)
4 - сурет
Үшбұрыштар теңдігінің екінші белгісі бойынша ( шарты бойынша CF=BF, 1 = 2 вертикаль бұрыштар, 3 = 4 айқыш бұрыштар ) DFC және GFB үшбұрыштары тең болады. Осыдан DF= GF шығады, демек, EF кесіндісі AGD үшбұрышының орта сызығы болады. Үшбұрыштың орта сызығы туралы теоремадан EF орта сызығы AB - ға параллель және EF= 12 AG болады. AB CD болғандықтан, EF кесіндісі екі табанына да параллель болады және EF= 12 AG= 12 AB+BG=12(AB+CD). ∎
Трапецияның орта сызығын табудың формулары
1.Трапецияның орта сызығын оның табаны, биіктігі және табанындағы бұрыштары арқылы есептеу:

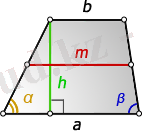
5 - сурет
Мұндағы, b- жоғарғы табаны, а - төменгі табаны, α,β- трапецияның табанындағы бұрыштары, h- биіктігі, m- орта сызығы болса, онда
m=a-h∙ctg α+ctg β2 немесе m=b+h∙ctg α+ctg β2
2. Трапецияның орта сызығын оның диагональдары, олардың арасындағы бұрышы және биіктігі арқылы есептеу:

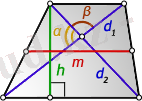
6 - сурет
Мұндағы, d1,d2 - диагональдары, α,β- трапецияның диагональдардың арасындағы бұрыштары, h- биіктігі, m- орта сызығы болса, онда
m=d1d22hsinα=d1d22hsinβ

1.3. Трапецияның екінші орта сызығы

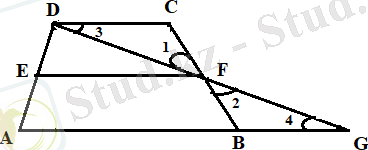
Трапецияның екінші орта сызығы деп оның табандарының орталарын қосатын кесіндіні айтады (7 - сурет).

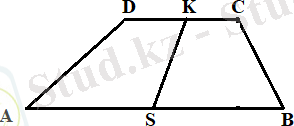
7 - сурет
KS - ABCD трапециясының екінші орта сызығы. Трапецияның бірінші орта сызығы оның табандарының қосындысының жартысына тең. Ал трапецияның екінші орта сызығы мен оның бүйір қабырғаларының арасында байланыс бар ма? Әлбетте, трапецияның екінші орташа сызығы бүйір жақтарының жарты жартысына тең емес, ең болмағанда табандарының бірінің созсақ та оның екінші орта сызығы өзгермейтіндігіне көз жеткізуге болады (8 - сурет).

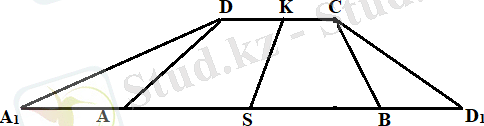
8 - сурет
Сонда да трапецияның екінші орта сызығы мен бүйір қабырғаларының арасындағы байланыс бар. Векторлық әдісті қолданамыз:
ABCD трапециясында (7 - сурет) DC AB, KS - екінші орта сызық.
KS=KD+DA+AS немесе KS=KC+CB+DS
Екі теңдікті қосысақ,
2KS=KD+KC+DA+CB+(AS+BS)
теңдігін аламыз. Одан KS=12 (DA+CB ).
Қорыта айтқанда, трапецияның екінші орта сызығының векторы (жоғарыдан төменге алынған) бүйір қабырғаларының векторларының қосындысының жартысына тең.

1.4. Трапецияның үшінші орта сызығы

Трапецияның үшінші орта сызығы деп оның диагональдарының орталарын қосатын кесіндіні айтады.
Трапецияның үшінші орташа сызығы оның табандарына параллель және олардың айырмасының жартысына тең:

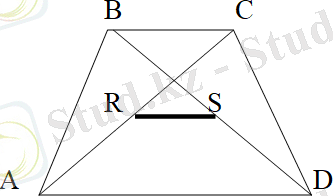
9 - сурет
RS=12 AD-BC. RS BC , RS - үшінші орта сызық.

1.5. Трапецияның орта сызықтарының қасиеттері

1.Трапецияның бірінші және екінші орта сызықтары қиылысу нүктесінде екіге бөлінеді.

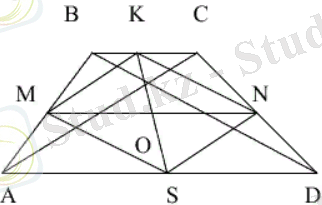
10 - сурет
Дәлелдеуі. BCD және ABD үшбұрыштарын қарастырайық (10 - сурет): KN- BCD үшбұрышының орта сызығы, KN BD және KN = 12 BD. MS - ABD үшбұрышының орта сызығы, MS BD , MS = 12 BD. Бұдан, МК АС, 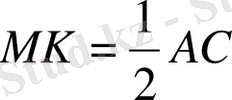, NS AC, 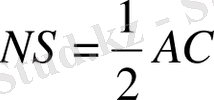. Осылайша, , MKNS - параллелограмм, MN және KS - оның диагональдары ,сондықтан, KO = OS, MO = ON.
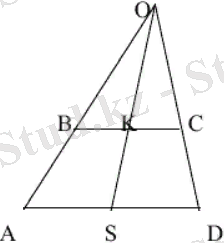
2.Трапецияның екінші орта сызығы оның диагональдарының қиылысу нүктесі арқылы өтеді.

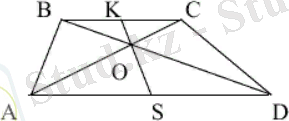
11 - сурет
Берілгені: ВК = КС
Дк: AS = SD
Дәлелдеуі. BD - BC AD екі түзудің қиюшы түзу болғандықтан CBD=BDA. BOK = SOD - вертикаль бұрыштар. ΔBOK және ΔSOD, ΔKOC және ΔAOS үшбұрыштары ұқсас үшбұрыштар.
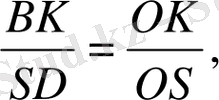
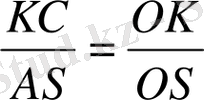. Бұл теңдіктерден 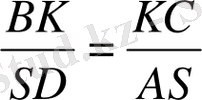, ал одан BK = KC (шарт бойынша ), онда AS = SD .
3.Трапецияның екінші орта сызығынан тұратын түзу бүйір қабырғаларынан тұратын түзулердің қиылысу нүктесі арқылы өтеді.

12 - сурет
Дәлелдеуі. Дәлелдеу үшін ΔВОС және ΔAOD қарастырайық. Олар екі бұрышы бойынша ұқсас,
OD↑↑OC,OB↑↑OA, OA=k∙OB,OD=k∙OC
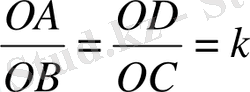
Кесіндінің ортасын табу формуласы бойынша
OK=12 OB+OC, OS= 12 OA+OD, OS=12 k∙OB+k∙OC=
= 12 kOB+OC=k∙OK OK және OS коллинеар, 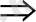O ∈KS.
Кері жору: Түзу бүйір қабырғаларынан тұратын түзулердің қиылысу нүктесі және бір табанының ортасы арқылы өтетін болса, онда ол екінші табанының ортасы арқылы да өтеді ( трапецияның екінші орта сызығы болып табылады).
Берілгені: OS түзуі ABCD трапециясының AD табанының ортасы арқылы өтеді.
Дк: ВК = КС
Дәлелдеуі:
11- сурет бойынша
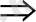
∆KOC ~ ∆SOD 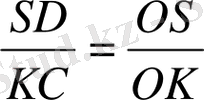∆ВОК ~ ∆AOS
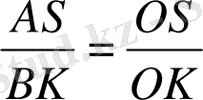
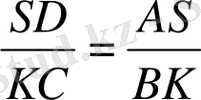, т.к. АS = SD( шарт бойынша), онда КС = ВК.
4.Теңбүйірлі трапецияның барлық орта сызықтары перпендикуляр.

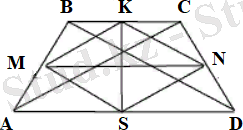
13 - сурет
Берілгені: ABCD - трапеция, AB=CD, MN,KS - орта сызықтары (13- сурет)
Дк: MN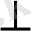KS
Дәлелдеуі:
MK - орта сызық ∆АВС, МКАС, МК=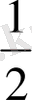АС
NS - орта сызық ∆ADC, NSAC, NS =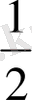АС
Егер MKNS төртбұрышының қарама - қарсы қабырғалары тең және параллель болса, онда MKNS - параллелограмм және ABCD - теңбүйірлі трапеция, сондықтан AC= BD.
MK = 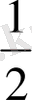АС, KN = 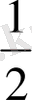BD, MK = KN, MKNS - ромб
Ромбының қасиеті бойынша, оның диагональдары перпендикуляр, сондықтан MNKS.
5.Теңбүйірлі трапецияның екінші орта сызығы мен табандары перпендикуляр болады. ( дәлелдеуі алдыңғы дәлелдеу сияқты)
6.Егер трапецияның бірінші және екінші орта сызықтары тең болса,онда оның диагональдары перпендикуляр (14 - сурет).

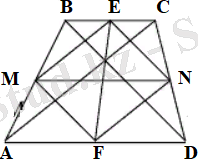
14 - сурет
Дәлелдеуі: МЕNF - параллелограмм, шарт бойынша MN=EF. Егер параллелограммның диагональдары тең болса, онда бұл параллелограмм - тік төртбұрыш, EN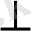ME. Егер ENBD, MEAC,онда BD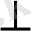AC.
Кері жору: егер трапецияның диагональдары перпендикуляр болса, онда бұл трапецияның орта сызықтары ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.