Квадрат теңдеудің шығу тарихы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

Квадрат теңдеудің шығу тарихы

XVI ғасырда италияның математиктері Тарталья мен Кардано үшінші
Алгебраға әріптік символикалардың енуі теңдеулерді шешу әдістері ұғымын
Көне заманда алгебраға қарағанда геометрия көбірек жетілген кезде, квадрат
теңдеулерді алгебралық жолмен емес геометриялық жолмен шеше білген. Әйгілі
әл-Хорезмидің Әл-жебр кітабынан мысал келтірейік. х 2 +10х=39 теңдеуін
шешейік. Мысал-2: Шешуі: қабырғасы х болатын квадратты қарастырайық. Оның
қабырғаларының бойында тікбұрыштар әрбір қабырғасы тең болатындай етіп
тұрғызылады. Олардың әрқайсысының аудандары 2 х-ке тең. Алынған фигураның
төрт бұрышына қабырғаларының әрқайсысы 2 болатын, ал ауданы 6 болатын төрт
бірдей квадратпен ABCD жаңа квадраты толғанша толтырамыз. D x С АВСD
квадратының ауданы (S-ті) мына ауданның қосындысы түрінде сипаттауға
болады: алғашқы х 2 – квадраттан, төрт тіктөртбұрыштан (4· 2 =10х) және
тұрғызылған 4 квадраттан (4·6 =25), яғни S=x2 +10x+25. х2 +10x өрнегін 39
санымен ауыстыра отырып, S=39+25=64-ті аламыз, бұл жерден ABCD қабырғасы,
яғни АВ=8 екендігі шығады. Алғашқы квадраттың ізделінді х-қабырғасы үшін: А
х В х=8-2 -2 =3 екенін аламыз. 10-тәсіл:квадраттық теңдеуді шешудің
графикалық шешімі. Егер x 2 +px+q=0 теңдеуінде екінші және үшінші мүшені
теңдеудің оң жағына шығаратын болсақ: x 2 =-px-q Енді y=x 2 және y=-px-q
функцияларының графиктерін саламыз. Бірінші функция графигін санақ басынан
өтетін парабола, ал екінші функцияның графигі түзу.Олар қиылысып
өтетіндіктен, қиылысу нүктелерін анықтай аламыз.Келесі шарттар орындалуы
мүмкін: Түзу мен парабола қиылысып, олардың қиылысу нүктелері екеу болуы
мүмкін. Абсциссадағы нүктелер берілген квадраттық теңдеудің түбірлері
болады. - Түзу мен парабола қиылысады, бірақ қиылысу нүктесі бір ғана нүкте
болғандықтан, түбірі бір ғана болады. - Түзу мен параболаның еш ортақ
нүктелері болмаса, онда квадраттық теңдеуде түбірі болмайды. Мысал: 1. x 2
-3x-4=0 квадраттық теңдеуін шешйік. Шешуі.Бұл теңдеуді мынадай түрге
келтіріп жазып алайық: x 2 -=3x+4 Енді координаталық жазықтықта у=3x+4
түзуін құрастырамыз.Қиылысқан нүктелерінің координаталары М(0;4) және N
(3;13).Түзу мен парабола екі нүктеде қиылысады.Олар А және В.Түбірлері x1=-
1 x2=4 Жауабы: x1=-1 x2=4

1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу

Мысал: х2+4х+3 =0 теңдеуін шешейік.
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х2+х+3х+3 =х(х+1)+3 (х+1) =(х+1)(х+3)
Демек, теңдеуді былай жазуға болады: (х+1)(х+3) =0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі
нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х=-
1 және сандары х2+4х+3=0 теңдеуінің түбірлері болып табылады.

2-әдіс. Толық квадратқа келтіру әдісі
Мысал: х2+8х-9=0 теңдеуін шешейік.
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х2+8х өрнегін
төмендегідей жазып аламыз: х2 + 8х=х2+2х4
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы
х пен 4-тің екі еселенгені. Толық квадрат алу үшін 42-ын қосу керек.
Сонда х2+2х4+42=(х+4)2
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 42-ын қосып,
алып тастаймыз. Сонда шығатыны: х2+8х-9=х2+2х4+42-9-4=(х+4)2-
25
Сонымен, берілген теңдеуді былайша жазуға болады: (х+4)2-25=0 , яғни
(х+4)2=25.
Бұдан х+4=5, х=1 немесе х+4=-5,
х= -9. Жауабы: 1;-9

3-әдіс. Квадраттық теңдеулерді формула арқылы шешу
ах2+вх+с=0, а≠0 теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі
өрнекті аламыз:
4а2х2+4ахв+4ас=0
((2ах)2+4ахв+в2)-в2+4ас=0 , (2ах+в)2=в2-4ас
2ах+в= , 2ах = -в
х= (1)
Оған келесідегідей мысалдар келтіруге болады:
1)3х2-7х+4=0 теңдеуін шешейік.
а=3, в=-7, с=4. Д=в2-4ас=(-7)2-4·4·3=49-
48=1.
Д0 болғандықтан, екі әр түрлі түбір болады: х1=1, х2=
Сонымен, дискриминант оң болғанда, яғни в2-4ас0, ах2+вх+с=0 теңдеуінің екі
түрлі түбірі болады.
2)9х2+6х+1=0 теңдеуін шешейік.
а=9, в=6, с=1. Д=в2-4ас=62-4·9·1=0.
Д=0 болғандықтан, бір ғана түбір бар болады: х=, х=
Сонымен, егер дискриминант нөлге тең болса, яғни в2-4ас=0, ах2+вх+с=0
теңдеуінің жалғыз
түбірі бар болады: х=
3)х2+2х+3=0 теңдеуін шешейік.
а=1, в=2, с=3. Д=в2-4ас=4-4·3·1= -8.
Д0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды.
Сонымен, егер дискриминант теріс болса, яғни в2-4ас0, онда ах2+вх+с=0
теңдеуінің түбірі болмайды.

4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу
Келтірілген түбірлері Виет теоремасын қанағаттандырады.
Ол былай беріледі: а=1 болғанда,
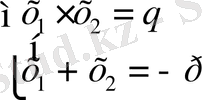
Бұдан келесі тұжырымдарды шығаруға болады:
а) Егер q (1) теңдеудің бос мүшесі оң болса (q0) онда теңдеудің
екі бірдей таңбалы түбірі болады. Егер р0, онда екі түбірі де теріс
болады, егер р0, онда түбірлері оң болады.
Мысал, 1)х2-9х+20=0, х1=4, х2=5, мұнда q=20 0, р=-9 0;
2)х2+5х+6 =0, х1 =-2, х2 =-3, мұнда q =6 0, р =5 0.
б) Егер q (1) теңдеудің бос мүшесі теріс болса (q 0), онда теңдеудің
екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң
болады, егер р 0 болса, теріс болады, егер р 0. Мысал, 1) х2+3х-4 =0; х1
=-4, х2 =1 мұнда q =-4 0, р=-3 0
2) х2-7х-8 =0; х1 =8, х2 =-1 мұнда q =-8 0, р =-
7 0
ax2+bx+c=0 (a≠0) квадраттық теңдеуінің D=b2-4ac дискриминанты оң болғанда
бұл теңдеудің екі 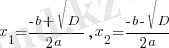шешімі бар болатының квадраттық теңдеу сабағында
айтылған.
Бұл формулалар теңдеудің шешімдерін теңдеудің коэфициенттері арқылы табуға
мүмкіндік береді.

Кері жағдайда, яғни x1 пен x2 белгілі ал a,b,c белгісіз болғанда Виет
теоремасын қолдана аламыз:
Виет теоремасы
ax2+bx+c=0 теңдеуінің шешімдері x1 пен x2 болса онда мына формулалар
орынды:
x1·x2=
x1+x2=
Мысалы x1=1, x1=3 ал теңдеуіміз белгісіз болсын, Виет теоремасы бойынша:
=x1·x2=1·3=3
=x1+x2=1+3=4
ax2+bx+c=0 теңдеуінің x2+x+=0 теңде уіне эквиваленттігін
пайдалансақ онда біздің теңдеуіміз мына түрге келеді:
x2+x+=x2-4x+3
Яғни x2-4x+3=0.
Ескерту.

a=1 десек онда ax2+bx+c=0 теңдеуі x2+bx+c=0 т еңдеуіне айналады және Виет
теоремасы мынандай болады:
x1·x2=c
x1+x2=-b.

5-әдіс. Теңдеуді асыра лақтыру әдісімен шешу
ах2+вх+с =0 , а ≠0 квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да
а-ға көбейтіп, мынаны аламыз: а2х2+авх+ас=0. ах =у деп белгілесек, х =
. Олай болса у2+ву+ас =0 теңдеуіне келеміз. Бұл бастапқы теңдеумен
тең. Теңдеудің түбірлерін у1, у2 –ні Виет теоремасы арқылы табамыз.
Соңында х1 =, х2 = -ны аламыз. Бұл жағдайда
а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті асыра
лақтыру әдісі деп атайды [1,13бет]. Бұл әдісті көбінесе Виет теоремасын
пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда
қолданады.
Мысал: 2х2-9х+9=0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз,
нәтижесінде
у2-9у+18=0 теңдеуін аламыз. Виет теоремасы бойынша
Жауабы: 3; 1, 5.
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану
ах2+вх+с=0, а≠0 квадрат теңдеуі берілген.
Егер а+в+с=0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х1=1,
х2=
Мысал: 7+2-9=0 қосындысы 0-ге тең. Осы үш сан үшін квадрат теңдеу
құрастырып, оны шешейік:

7-әдіс. Квадрат теңдеуді циркуль және сызғыш көмегімен шешу
ах2+вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен шешу
әдісін ұсынамыз (1-сурет). Ізделінді шеңбер абцисса өсінде В(х;0) және
Д (х2;0) нүктелерінде қиылыссын делік. Мұндағы х1, х2 - ах2 + вх + с=0
теңдеуінің түбірлері және ординат осінен А(0;1) және С(0;) нүктелері
арқылы өтеді делік. Олай болса, қима туралы теорема бойынша мынаны аламыз:

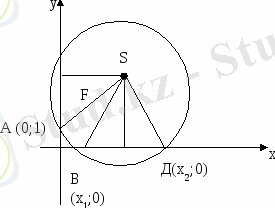
1-сурет

ОВ·ОД=ОА·ОС,
бұдан ОС=

Шеңбер центрі АС және ВД хорда ортасында орналасқан перпендикуляр SF пен
SК-ның қиылысу нүктелері болып табылады, сондықтанSК=;
SF =
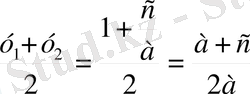
Сонымен,
1) S 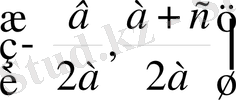(шеңбер центрі) және А (0;1) нүктелерін тұрғызамыз;
2) SА радиусты шеңбер жүргіземіз;
3) Осы шеңбердің Ох осі арқылы өтетін қиылысу нүктелері бастапқы квадрат
теңдеудің түбірі болады.
Сонымен үш түрлі жағдай болуы мүмкін:
1-ші жағдай.Шеңбер радиусы ордината центрінен артық (АS SК, немесе,
шеңбер Ох осін екі нүктеде (2а-сурет) В (х; 0) және Д
(х2;0) нүктелерде қияды. Мұндағы х1 және х2-ах2+вх+с =0 квадрат теңдеуінің
түбірлері).
2-ші жағдай.
Шеңбер радиусы ордината центрінде (АS= SК; немесе тең, шеңбер Ох осін
В (х1; 0) нүктесінде (2б)-сурет) жанап өтеді, мұндағы х1 – квадрат
теңдеудің түбірі).
3-ші жағдай.
Шеңбер радиусы ордината центрінен кіші (А S SК, немесе ) кем,
щеңбердің абцисса осімен қиылысатын нүктесі жоқ (2в – сурет), бұл жағдайда
теңдеудің шешімі болмайды.

у у у

2-сурет
а) АSSВ, екі шешімі бар: х1 және х2
б) АS=SВ, бір шешімі бар: х1
в) АSSВ, шешім жоқ.

8-әдіс. Квадрат теңдеуді номограмма көмегімен шешу

O B E
y 3

F D

y
y 3y
H A

C
3
3y 9
p q 3-сурет

4- сурет
Бұл квадрат теңдеуді шешудің бұрынғы және жөнсіз ұмыт болған әдісі.
Брадис таблицасында z2+pz+q=0 теңдеуін шешуге арналған номограмманы
қарастырайық. Бұл номограмма ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.