Көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

ТҮРКІСТАН ОБЛЫСЫНЫҢ АДАМИ ӘЛЕУЕТТІ ДАМЫТУ БАСҚАРМАСЫНЫҢ «Д. ҚОНАЕВ АТЫНДАҒЫ АГРАРЛЫҚ -ТЕХНИКАЛЫҚ КОЛЛЕДЖ» МКҚК

Математика пәні оқытушысы: Д. Сайдазованың

«Көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері» тақырыбы бойынша

Әдістемелік нұсқау

Түркістан 2021

Көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері.

Құрастырған: Д. Р. Сайдазова

Математика пәні бойынша әдістемелік нұсқау Түркістан облысы «Д. Қонаев атындағы аграрлық техникалық колледжі» МКҚК.

«Жаратылыстану пәндері» әдістемелік бірлестігі отырысында қаралған.

Хаттама №

ӘБ төрағасы: У. Ташметов

Баспаға Д. Қонаев атындағы аграрлық техникалық колледжі математика пәнінен «Көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері» тақырыбындағы әдістемелік нұсқаулықты әдістемелік кеңесі ұсынған.

Еліміздің болашағы - бүгінгі жас ұрпақтың қолында,

Жас ұрпақтың болашағы - бүгінгі ұстаздың қолында”.

Н. Ә. Назарбаев.

«Көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері» тақырыбындағы әдістемелік нұсқаулық

Мазмұны:

1. Кіріспе4

2. Көрсеткіштік функция5

3. Көрсеткіштік теңдеулер5

4. Логарифмдік функция11

5. Логарифмдік теңдеулер 12

6. Қолданылған әдебиеттер23

Кіріспе

Қазіргі кезде математика пәнінен оқытуда оқушылардың көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері үйрету өте маңызды. Өйткені бұл тақырыптағы тапсырмалар ҰБТ тестінде келеді. Математиканы оқыту есеп шығаруды үйрету ғана емес, ол кез келген проблеманы шеше білуге, қиындықты жеңуге маңызды роль атқарады. Көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері математика курсында мазмұны жағынан да, оқу - дамытушылық әрекеті жағынан да негізгі орындардың біріне ие. Сонымен қатар көрсеткіштік, логарифмдік функциялар және олардың теңдеулерін шешу тәсілдері оқушыларға квадрат, сызықтық теңдеулер тақырыбымен байланысқан. Бұл тақырып бойынша алған білімдерін жүйелеп, алгебра бойынша алған білімдерімен байланыс орнатуға мүмкіндік береді. Бұл әдістемелік құрал оқушылар мен пән мұғалімдері үшін көмекші анықтамалық құрал ретінде құрастырылған. Негізгі қарастырылған тақырыптар:көрсеткіштік функция, көрсеткіштік теңдеулер, логарифмдік функция, логарифмдік теңдеулер.

Осы әдістемелік құрал оқушылардың ой - танымын қалыптастырып, өзіндігінен жұмыс жасай білуге, ізденімпаздығын, ҰБТ-ға дайындық деңгейін арттыруға өзіндік үлесін тигізеді.

Көрсеткіштік функция

y=a ^x (а≠1, а>0) түріндегі берілген функция көрсеткіштік функция деп аталады.

Анықтаманың тұжырымдасында берілген төмендегі ұйғарымдарға назар аудару қажет.

а негізі 1 санына тең болмауы керек (а≠1), өйткені а=1 болғанда ахдәрежесінің мәні 1 санына тең болып, х айнымалысына тәуелді болмайды;
а негізі оң сан болуы керек( а>0), себебі а<0 болғанда х-тің үшін ахдәрежесі нақты сан болмайды.

Мысалы, а =-3 және х =1/2 болғанда, а ^х дәрежесі мына түрге келеді:

(-3) ^1/2 = 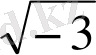, ал бұл нақты сан емес .

3) а негізі бөлшек болған а ^х дәрежесі қандай да бір дәрежедегі түбірді білдіреді, онда түбір мәндерінің ішінен тек қана арифметикалық түбір алынады.

Көрсеткіштік теңдеулер

Айнымалысы дәреженің көрсеткішінде болатын теңдеуді көрсеткіштік теңдеу деп атайды. Көрсеткіштік теңдеулердің ең қарапайым мысалы $a^{x} = b\ \ (мұндағы\ a > 0, \ a \neq 1) .$

Көрсеткіштік теңдеулерді шешудің бірнеше әдісін қарастырайық.

Теңдеудің екі жағы бір негізге келтіру әдісі

$a^{f(x) } = a^{g(x) }$ түріндегі теңдеудің шешімі (мұндағы $a > 0, \ a \neq 1)$

f(x) =g(x) теңдеудің шешімімен мәндес.

Тапсырма 1:

Шешуі:

Теңдеуді шешіңіз: $\left( \frac{3}{7} \right) ^{3x - 7} = \left( \frac{7}{3} \right) ^{7x - 3}$

Шешуі:

$\left( \frac{3}{7} \right) ^{3x - 7} = \left( \frac{7}{3} \right) ^{7x - 3}$

$\left( \frac{3}{7} \right) ^{3x - 7} = \left( \frac{3}{7} \right) ^{- (7x - 3) }$

3x-7=-7x+3

x=1

Жауабы: 1.

Тапсырма 2

Шешуі:

Теңдеуді шешіңіз:

3 ^2х+5 = 3 ^x+2 + 2

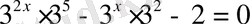
3 ^x = yдеп жаңа айнымалы енгізіп, берілген теңдіктен мынадай квадрат теңдеу аламыз. 243у ² -9у-2=0

Бұл квадрат теңдеудің түбірлері мынаған тең.

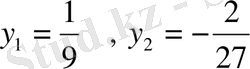
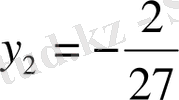теріс, ал 3 ^x < 0 болуы мүмкін емес, сондықтан алмастыру шарты бойынша 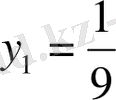түбірін аламыз. Табылға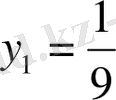н мәнін

3 ^x =y теңдігіне қоямыз: 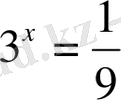, , 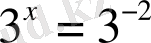х=-2

Тексеру жүргіземіз : 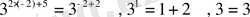, Жауабы : -2

Тапсырма 3:

Шешуі:

Теңдеуді шешіңіз: $2^{x^{2} - 6x - \frac{5}{2}} = 16\sqrt{2}$

Шешуі:

$2^{x^{2} - 6x - \frac{5}{2}} = 16\sqrt{2}$

$2^{x^{2} - 6x - \frac{5}{2}} = 2^{4} \bullet 2^{\frac{1}{2}}$

$x^{2} - 6x - \frac{5}{2} = 4 + \frac{1}{2}$

$x^{2} - 6x - 7 = 0$

$x_{1} = - 1; \ x_{2} = 7$

Жауабы:{-1; 7}.

Тапсырма 4:

Шешуі:

Теңдеуді шешіңіз: 25 ^1-2х= 5 ^4-6x

25 ^1-2х =5 ^4-6x

5 ^21-2х =5 ^4-6x

2*1-2x=4-6x

1-2x=2-3x

$1) \left\{ \begin{array}{r} 1 - 2x = 2 - 3x \\ 1 - 2x \geq 0 \end{array} \rightarrow \left\{ \begin{array}{r} x = 1 \\ x \leq \frac{1}{2} \end{array} \rightarrow \varnothing \right. \ \right. \$

$2) \left\{ \begin{array}{r} 1 - 2x = - (2 - 3x) \\ 1 - 2x < 0 \end{array} \rightarrow \left\{ \begin{array}{r} x = \frac{3}{5} \\ x > \frac{1}{2} \end{array} \rightarrow x = \frac{3}{5} \right. \ \right. \$

Жауабы: $\frac{\mathbf{3}}{\mathbf{5}}$

Тапсырма 5:

Теңдеуді шешіңіз : $\frac{\mathbf{1}}{\mathbf{27}}\mathbf{\bullet}\sqrt[\mathbf{4}] {\mathbf{9}^{\mathbf{3x - 1}}}\mathbf{=}\mathbf{27}^{\frac{\mathbf{2}}{\mathbf{3}}}$

Шешуі:

$\frac{1}{27} \bullet \sqrt[4] {9^{3x - 1}} = 27^{\frac{2}{3}}$

$3^{- 3} \bullet 3^{\frac{2(3x - 1) }{4}} = 3^{3\left( - \frac{2}{3} \right) }$

$3^{- 3 + \frac{3x1}{2}} = 3^{- 2}$

$- 3 + \frac{3x - 1}{2} = - 2$

х= 1 Жауабы: 1

Тапсырма 6:

Теңдеуді шешіңіз : 5 ^x+1 -5 ^x =100

Шешуі:

5 ^x+1 - 5 ^x = 100

5 * 5 ^x -5 ^x =100

4*5 ^x =100

5 ^x =25

х=2 Жауабы: 2

Тапсырма 7:

Теңдеуді шешіңіз : $\mathbf{7}^{\mathbf{x + 2}}\mathbf{-}\frac{\mathbf{1}}{\mathbf{7}}\mathbf{\bullet}\mathbf{7}^{\mathbf{x + 1}}\mathbf{- 14 \bullet}\mathbf{7}^{\mathbf{x - 1}}\mathbf{+ 2 \bullet}\mathbf{7}^{\mathbf{x}}\mathbf{= 48}$ Шешуі:

$7^{x + 2} - \frac{1}{7} \bullet 7^{x + 1} - 14 \bullet 7^{x - 1} + 2 \bullet 7^{x} = 48$

$7^{2} \bullet 7^{x} - \frac{1}{7} \bullet 7 \bullet 7^{x} - 14 \bullet \frac{1}{7}7^{x} + 2 \bullet 7^{x} = 48$

$7^{x} \bullet (48 - 1 - 2 + 2) = 48$
$7^{x} = 1 = 7^{{^\circ}}$

$\mathbf{x = 0}$ Жауабы: 0

Жаңа айнымалы енгізу әдісі

Аа ^2х +Ва ^x +С=0 түріндегі теңдеу a ^x =y белгілеуін енгізу арқылы Ay ² +By+C=0 $\mathbf{\ }\$ квадрат теңдеуіне келтіріледі.

Тапсырма 8:

Теңдеуді шешіңіз : $\mathbf{4 \bullet (}{\frac{\mathbf{3}}{\mathbf{2}}\mathbf{) }}^{\mathbf{2x}}\mathbf{+ 15 \bullet (}{\frac{\mathbf{3}}{\mathbf{2}}\mathbf{) }}^{\mathbf{x}}$ =54 Шешуі:

$({\frac{3}{2}) }^{x}$ =t Белгілеуін енгізіп теңдеуді қайта жазайық:

4t ² +15t-54=0

(4t-9) (t+6) =0

$t = \frac{9}{4}; t \neq - 6( < 0)$

$({\frac{3}{2}) }^{x} = \frac{9}{4}$

X=2 Жауабы: 2

Тапсырма 9:

Теңдеуді шешіңіз : 9 ^x-1 -3 ^x+1 +3 ^x-3 =1

Шешуі:

3 ^{2(x-1) -} 3 ^x+1 +3 ^x-3 =1

$\frac{1}{9} \bullet 3^{2x} - 3 \bullet 3^{x} + \frac{1}{27} \bullet 3^{x} = 1$

$\frac{1}{9} \bullet 3^{2x} - \frac{801}{27} \bullet 3^{x} - 1 = 0\ \left \bullet (27) \right. \$

$3 \bullet 3^{2x} - 80 \bullet 3^{x} - 27 = 0$

3 ^x = t белгілеуін енгізіп теңдеуді қайта жазайық.

${3t}^{2} - 80t - 27 = 0$

$(3t + 1) (t - 27) = 0$

$t = 27; t \neq - \frac{1}{3}( < 0)$

3 ^x =27

X=3 Жауабы: 3

Тапсырма 10:

Теңдеуді шешіңіз : $5^{x} - 24 = \frac{25}{5^{x}}$

шешуі $5^{x} - 24 = 25 \bullet \frac{1}{5^{x}}$

$5^{x} - 25 \bullet \frac{1}{5^{x}} - 24 = 0$

5 ^x = t белгілеуін енгізіп теңдеуді қайта жазамыз.

$t - 25 \bullet \frac{1}{t} - 24 = 0$

$t^{2} - 25t - 25 = 0$

$(t - 25) (t + 1) = 0$

$t = 25; t \neq - 1\ ( < 0$

$5^{x} = 25$

$x = 2$ Жауабы: 2

Тапсырма 11:

Теңдеуді шешіңіз $9^{x^{2} - 1} - 36 \bullet 3^{x^{2} - 3} + 3 = 0$

Шешуі:

$\frac{3^{{2x}^{2}}}{9} - 36 \bullet \frac{1}{27} \bullet 3^{x^{2}} + 3 = 0$

$\frac{3^{{2x}^{2}}}{9} - \frac{41}{3} \bullet 3^{x^{2}} + 3 = 0$

$3^{{2x}^{2}} - 12 \bullet 3^{x^{2}} + 27 = 0$

$3^{x^{2}} = t$ белгілеуін енгізіп теңдеуді қайта жазамыз.

$t^{2} - 12t + 27 = 0$

$(t - 3) (t - 9) = 0$

T=3; t=9

$1) \ 3^{x^{2}} = 3^{1\ \ \ \ \ \ }\ \ \ \ \ \ \ \ 2) 3^{x^{2}} = 9 = 3^{2}$

$x^{2} = 1x = \pm 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x^{2} = 2 = x = \pm \sqrt{}2$

Жауабы: $\left\{ \pm 1; \ \ \pm \sqrt{}2 \right\}$

Логарифмдік функция

Көрсеткіштік функцияға кері функция логарифмдік функция деп аталады

Логарифмдік функцияның қасиеттері

Анықталу облысы оң сандар жиыны, яғни R+
Мәндер жиыны барлық нақты сандар жиыны, яғни R
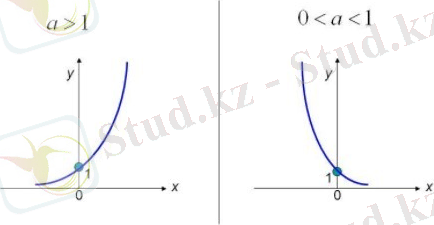
а > 1 болғанда функция өседі; 0 < а < 1 болғанда функция кемиді
Функция өзінің анықталу облысында үзіліссіз

Ондық логарифм

Негізі 10 болатын санның логарифмі ондық логарифм деп аталады

Натурал логарифм

Негізі e болатын санның логарифмі натурал логарифм деп аталады

Логарифмнің негізгі қасиеттері:

1) негізі а ( а - кез келген оң сан) болатын а санының логарифмі бірге тең:

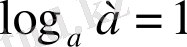
2) негізі а болатын бір санының логарифмі нөлге тең:

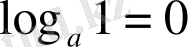
3) екі немесе бірнеше оң сандардың көбейтіндісінің логарифмі көбейткіштердің логарифмдерінің қосындысына тең:

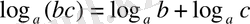
4) қатынастың немесе бөлшектің логарифмі алымының логарифмі мен бөлімінің логарифмінің айырымына тең:

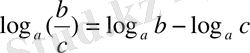
5) дәреженің логарифмі дәреже көрсеткішін дәреже негізінің логарифміне көбейткенге тең:

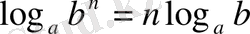
6) жаңа негізге көшу формуласы:

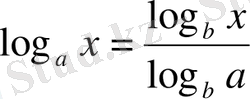
Логарифмдік функцияның графигі

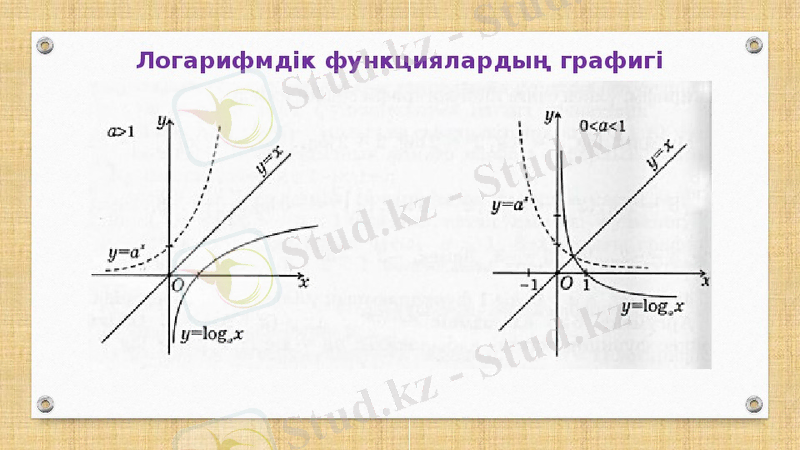
Логарифмнің негізгі қасиеттеріне мысал

$\log_{3}x = - 1$ (Жауабы: $\frac{1}{3}$ )

$\log_{5}x = 2$ (Жауабы:25)

$3^{\log_{3}27}$ (Жауабы:27)

$\log_{2}\sqrt{2}$ (Жауабы: $\frac{1}{2}$ )

${\ \ \ \ \ \ log}_{3}(243 \bullet 729)$ (Жауабы:11)

Логарифмдік теңдеулер

Айнымалысы логарифм белгісінң ішінде болатын теңдеуді логарифімдік теңдеу деп атайды. Қарапайым логарифмдік теңдеудің түрі $\log_{a}x = b$ (мұндағы $a > 0, a \neq 1$ ) . Оның шешуі $x = a^{b}$ .

Күрделі логарифмдік теңдеулерді шешу алгебралық теңдеулерді немесе $\log_{a}x = b$ түріндегі қарапайым теңдеуді шешуге әкеледі.

Логарифмдік теңдеулерді шешуде, анықталу облысы оң сандар ғана болғандықтан, бөгде түбірлердің пайда болуы мүмкін. Сондықтан шыққан мәндерді теңдеуге қойып тексерген немесе анықталу облысында жатып-жатпайтынын анықтаған жөн.

Логарифмдік теңдеулерді шығару әдістері:

Логарифмнің анықтамасы негізінде шешу
Потенциалдау әдісі
Жаңа айнымалы еңгізу әдісі
Мүшелеп логарифдеу әдісі

Логарифмнің анықтамасы негізінде шешу

Логарифмнің анықтамасын қолдану арқылы шығарылатын теңдеулер

$\log_{x}\left( x^{3} - 5x + 10 \right) = 3$ теңдеуін шешейік. Логарифмнің анықтамасы бойынша

$x^{3} - 5x + 10 = x^{3}$

- 5x = - 10

х = 2

Табылған айнымалының мәнін теңдеуге қойып тексеру керек.

$\log_{2}\left( 2^{3} - 5 \bullet 2 + 10 \right) = \log_{2}2^{3} = 3$

х = 2 теңдеуді қанағаттандырады. Жауабы : 2

Логарифмдік функцияның анықталу облысы оң нақты сандар жиыны екені белгілі. Сондықтан логарифмдік теңдеулерді шығару кезінде алдымен айнымалының мүмкін болатын мәндер жиынын анықтайды

Тапсырма 1

Теңдеуді шешіңіз:

$\mathbf{\log}_{\mathbf{16}}\mathbf{x +}\mathbf{\log}_{\mathbf{4}}\mathbf{x +}\mathbf{\log}_{\mathbf{2}}\mathbf{x = 7}$