Келтірілген тұйық автоматты реттеу жүйесі орнықты болатын кездегі пропорционалдық С1 реттегішті баптау параметрлерінің мәндерінің аймағын зерттеу

Ғ. Даукеев атындағы «АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»

КОММЕРЦИЯЛЫҚ ЕМЕС АКЦИОНЕРЛІК ҚОҒАМ

ЖЫЛУ ЭНЕРГЕТИКА ЖӘНЕ ЖЫЛУ ТЕХНИКА ИНСТИТУТЫ

«ӨНЕРКӘСІПТІК ЖЫЛУ ТЕХНОЛОГИЯ» КАФЕДРАСЫ

№2 ЕСЕПТЕУ-ГРАФИКАЛЫҚ ЖҰМЫСЫ

Пән: «Жылутехнологиясындағы жылутехнологиялық процестерді АБТ және АБЖ»

Тақырыбы: Келтірілген тұйық автоматты реттеу жүйесі орнықты болатын кездегі пропорционалдық С1 реттегішті баптау параметрлерінің мәндерінің аймағын зерттеу.

Мамандық: 5В071700 Жылуэнергетика

Топ: ТЭ(ПТЭ) к-17-2

Сынақ кітапшасы: № 171175

Орындаған: Арман Айнур

Қабылдаған: доц. Джаманкулова Н. О.

« » 2020ж.

Бағасы қолы

Алматы, 2020

Мазмұны

Кіріспе . . . 3

1 Жалпы әдістемелік нұсқаулар . . . 4

2 Есептік-сызба жұмысының тапсырмалары . . . 5

3 Есептік-сызба жұмысының орындалуы . . . 7

2. 3. 1 Сұрақ жауабы . . . 7

Есеп . . . 8

Вышнеградский критериі бойынша АРЖ тұрақтылығын тексеру . . . 9

Гурвиц критерийі бойынша АРЖ орнықтылығын тексеру . . . 10

Михайлов критерийі бойынша АРЖ орнықтылығын тексеру . . . 11

Найквист критерийі бойынша АРЖ орнықтылығын тексеру . . . 13

Әдебиеттер тізімі . . . 15

Кіріспе

Қазіргі заманғы автоматты реттеу және басқару жүйелерінсіз жылутехникалық қондырғылардың сенімді, тиімді және қауіпсіз жұмыс істеуін қамтамасыз ету мүмкін емес.

Автоматты басқару жүйесіндегі жылутехникалақ объектілердің бірқатар ерекшеліктері бар, мысалы, өтпелі және кешігу кезеңдерінің болуы, параметрлерінің үлестірімділігі, белгілі шамада инерттілігі, динамикалық қасиеттерінің эксперимент жүзінде алынған мәндер жинағы бойынша берілуі т. с. с. Сондықтан автоматты басқарудың жалпы теориясының ішінен жылутехникалық және жылуэнергетикалық жүйелерді тиімді есептеуге мүмкіндік беретін әдістер тобын іріктеп алу қажеттігі туындайды.

Автоматтандырылған басқару жүйесі (АБЖ) - белгіленген мақсатқа сәйкес, күрделі үдерісті (нысанды) тиімді басқаруды қамтамасыз ететін математикалық әдістердің, техникалық құралдардың (ЭЕМ, байланыс құралдары, ақпаратты бейнелеу құрылғылары және т. б. ) және ұйымдастыру кешендерінің жиынтығы. АБЖ негізден және қызметтік бөліктен тұрады. Оның негізіне ақпараттық, техникалық және математикалық жасақтама кіреді. Қызметтік бөлікке басқарудың нақты функцияларын автоматтандыратын, өзара байланысты бағдарламалардың жиынтығын жатқызамыз. АБЖ маңызды міндеті - еңбек өнімділігін арттыру және басқару үдерістерін жоспарлау мен реттеу әдістерін жетілдіру негізінде нысанды (өндірістік, әкімшілік және т. б. ) басқару тиімділігін жоғарылату.

1 Жалпы әдістемелік нұсқаулар

1. 1 Бұл курсты оқитын студенттер бақылау жұмысын орындауы тиіс. Бақылау жұмысын орындау барысында берілген сұрақтарға жазбаша жауап беру және есептер шығару керек.

Орындалатын бақылау жұмысының нұсқасы студенттің фамилиясының бірінші әрпі (1 кестеге қара), сынақ кітапшасы шифрының соңғы және оның алдындағы сандары бойынша таңдалады.

1 Кесте

2. Есептік-сызба жұмысының тапсырмалары

1. ) Бақылау сұрақтарына жазбаша жауап беру керек. Бақылау

сұрақтардың нөмірлерін 2 кестеден таңдап алыңыз.

2 Кесте

2. ) 2-суретте келтірілген тұйық автоматты реттеу жүйесі орнықты болатын кездегі пропорционалдық (C ₁ ) реттегішті баптау параметрлерінің мәндерінің аймағын анықтаңыз.

Ескерту: зерттеуді Вышнеградский диаграммасын, Гурвиц, Михайлов және Найквист критерийлерін қолдана отырып жасау керек.

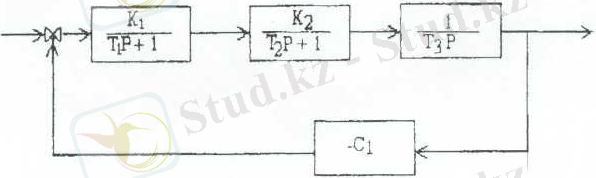
1 сурет

3 Кесте

3. Есептік-сызба жұмысының орындалуы

1. 2. 3. 1 Сұрақ. Сызықтық жүйелердің орнықтылығы туралы жалпы түсінік.

Жүйенің орнықтылығы деп оның тепе-теңдік күйінен ауытқуына себеп болған әсерді алып тастағаннан кейін, баспатқы орнықтылық қалпына оралу қабілеттілігін айтады.

Автоматты реттеу жүйесінің статикалық тепе-теңдік күйі әртүрлі болады. Жүйенің орнықтылық режиміндегі тепе-теңдік күйі үш түрге ажыратылады (12. 1 - сурет) :

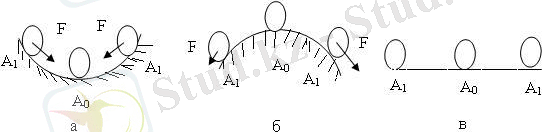
12. 1 сурет. Тепе-теңдік күйдің үш түрі:

а-орнықты; б-орнықсыз; в-бейтарап.

Тепе теңдік күйдің мүмкін болатын түрлерін алдымен беттің әртүрлі нүктелерінде орналасқан шариктің қозғалыс бағытынан қарастырайық: а) шарикті бастапқы тепе теңдік күйіне қайтарушы F күші шарик беттің қай жерінде жатса да пайда болады; б) шарик тепе-теңдік күйінен сәл ауытқыса F күші пайда болып, оны одан әрі тепе теңдік күйінен ауытқытуға тырысады; в) шарик беттің қай нүктесінде жатса да орнықты күйінде қалады.

Шарик мысалындағы тепе теңдік түрлері жөніндегі ұғымды автоматты реттеу жүйесінде де қарастыруға болады.

Жұмыс істеп тұрған автоматты жүйеге әртүрлі тұрақты сыртқы қозғалу әсері етуі салдарынан реттелетін шығыстық шаманың мәні жиі өзгеріп отырады. Жүйенің автоматты реттеуіші осы реттелетін шаманы берілген мәнге келтіруге ұмтылады. Бірақ тұтастай алғанда жүйеде инерциялық массалар, реактивті элементтер (индуктивті, сыйымдылық) болатындықтан, оның орнықты қалпына келуі, немесе қалыптасқан бір күйден келесісіне өтуі лезде емес, белгілі түрде кешігіп жүзеге асады. Жүйеде өтпелі процесс туындайды. Бұл жағдайда, егер жүйе қозу әрекеті тоқталғаннан кейін қалыптасқан күйге оралса, ол орнықты. Егер оралмаса, онда орнықсыз. Орнықсыз жұмыс кері байланыспен қамтылған АРЖ-ның барлығында туындауы ықтимал.

Автоматты жүйелере мынадай үш талаптар орындалуы қажет: орнықтылық шарты, өтпелі процеске және қалыптасқан режимге қойылатын талаптар АРЖ-ның орнатылығын анықтау мәселесі басты болып саналады, өйткені орнықсыз жүйелер іс жүзінде жарамсыз.

2. ) Есеп

$$К_{1} = \ 1$$

$$K_{2} = 0, 5$$

$$T_{1} = 10\ c$$

$$T_{2} = 25\ c$$

$$T_{3} = 35\ c$$

$${W(p) }_{об} = {\ W(p) }_{1}*\ {W(p) }_{2}*\ {W(p) }_{3}$$

$$W_{р}(p) = \ - \ C_{1}$$

$${W(p) }_{об}\ = \ W_{1}(p) *\ {W\ }_{2}(p) \ *\ W_{3}(p)$$

$${W(p) }_{об}\ = \frac{К_{1}}{T_{1}P + 1}*\frac{К_{2}}{T_{2}P + 1}*\frac{1}{T_{3}P}$$

${W(p) }_{об}\ = \frac{К_{1}К_{2}}{T_{1}{T_{2}T_{3}P}^{3} + T_{1}{T_{3}P}^{2} + T_{2}{T_{3}P}^{2} + T_{3}P}\ = \frac{К_{1}К_{2}}{T_{1}{T_{2}T_{3}P}^{3} + (T_{1}T_{3} + T_{2}T_{3}{) P}^{2} + T_{3}P}$

$$W(рег) = \ - \ C_{1}$$

$${W(p) }_{p} = \ - \ C_{1}$$

$${W(p) }_{p}*\ {W(p) }_{об}\ = 1$$

$${W(p) }_{p}*{\ W(p) }_{об}\ - 1\ = 0\$$

$\frac{К_{1}К_{2}( - \ C_{1}) }{T_{1}{T_{2}T_{3}P}^{3} + (T_{1}T_{3} + T_{2}T_{3}{) P}^{2} + T_{3}P} + 1\ = \ 0$

Жүйенің сипаттамалық теңдеуі:

$$T_{1}{T_{2}T_{3}P}^{3} + (T_{1}T_{3} + T_{2}T_{3}{) P}^{2} + T_{3}P + К_{1}К_{2}C_{1} = 0$$

$$a_{3}\ {р\ }^{3} + \ a_{2}\ р^{2}\ + \ a_{1}р\ + \ a_{0} = 0\ \$$

$$a_{3}\ = T_{1}T_{2}T_{3} = \ 10 \bullet 25 \bullet 35 = 8750$$

$${a\ }_{2}\ = \ T_{2}T_{3} + \ T_{1}T_{3} = 25 \bullet 35 + 10 \bullet 35 = 875 + 350 = 1225$$

$$a_{1} = \ T_{3} = 35$$

$$a_{0} = \ К_{1}К_{2}C_{1} = 1 \bullet 0, 5 \bullet \ C_{1} = 0, 5\ C_{1}\$$

1. Вышнеградский критериі бойынша АРЖ тұрақтылығын тексеру

Жүйенің сипаттамалық теңдеуі:

$$a_{3}\ {р\ }^{3} + \ a_{2}\ р^{2}\ + \ a_{1}р\ + \ a_{0} = 0\ \$$

$$8750{р\ }^{3} + {1225р}^{2} + 35р\ + 0, 5C_{1} = 0\ \$$

$a_{3} = \ 1$ кезіндегі Вышнеград коэффициенті критерийіне сәйкес.

Жаңа теңдеу:

$$\frac{a_{3}}{a_{3}}\ {р\ }^{3} + \ \frac{a_{2}}{a_{3}}\ р^{2}\ + \ \frac{a_{1}}{a_{3}}р\ + \ \frac{a_{0}}{a_{3}} = 0$$

$$\frac{8750}{8750}{р\ }^{3} + {\frac{1225}{8750}\ р}^{2} + \frac{35}{8750}\ р\ + \frac{0, 5C_{1}}{8750} = 0\ \$$

$a_{3} = \ 1;$ $a_{2} = \frac{1225}{8750}$ $a_{1} = \frac{35}{8750}$ ; $a_{0} = \frac{0, 5C_{1}}{8750}$

Вышнеград жүйесі өлшеміне сәйкес, егер шарттар орындалса, тұрақты:

$\mathbf{Х\ > \ 0}$ $\mathbf{Y > \ 0}$ $\mathbf{\ Х\ Y > 1}$

$Х\ = \frac{a_{2}}{\sqrt[3] {a_{0}}}\ \ \ \ \ \ \ Y\ = \ \frac{a_{1}}{\sqrt[3] {a_{0}^{2}}}\ \ \ \ \ \ \frac{a_{1}a_{2}}{a_{0}} > 1\ \ \ \ \$

$$\left\lbrack \left( \frac{35}{8750} \bullet \frac{1225}{8750} \right) /\frac{0, 5\ С1}{\ 8750} \right\rbrack\ \mathbf{> \ 1}$$

$C_{1} < \ 9, 8$ кезінде жүйе тұрақты болып табылады

2. Гурвиц критерийі бойынша АРЖ орнықтылығын тексеру

Өлшеміне сәйкес Гурвицтың сипаттамалық теңдеуінде барлық коэффициенттерінің бірдей белгісі болуы қажет және жеткілікті, ал Δ _n-1 анықтағышы және оның барлық диагональды минорлары оң болар еді:

a _n > 0 a _{n -1} > 0 … a ₁ > 0 a ₀ > 0

Δ _n-1 > 0 Δ _n-2 > 0 … Δ ₂ > 0 Δ ₁ > 0

Δ _n-1 = 0 жүйенің орнықтылық шегі

Жүйенің сипаттамалық теңдеуі:

$a_{3}\ {р\ }^{3} + \ a_{2}р^{2}\ + \ a_{1}р\ + \ a_{0} = 0\ \$ $n = 3$

$$8750{р\ }^{3} + {1225р}^{2} + 35р\ + 0, 5C_{1} = 0\$$

$$\mathrm{\Delta}_{3} = \left \begin{matrix} a_{2} & a_{0} & 0 \\ a_{3} & a_{1} & 0 \\ 0 & a_{2} & a_{0} \end{matrix} \right = \left \begin{matrix} 1225 & 0, 5C_{1} & 0 \\ 8750 & 35 & 0 \\ 0 & 1225 & 0, 5C_{1} \end{matrix} \right$$

Гурвица критерийіне сәйкес, Δ _n-1 анықтағышы және оның барлық диагональды минорлары оң болып табылады:

$\mathrm{\Delta}_{1} = a_{2} > 0$ $\mathrm{\Delta}_{1} = a_{2} = \ 1225 > 0$ $\Delta_{2} > 0\ \ \ \ \ \ \$

Δ _{n-1 =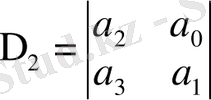} = a ₂ × a ₁ - a ₃ × a ₀ > 0

$\Delta_{2} = a_{2} \bullet a_{2} - a_{2} \bullet a_{2} = 1225 \bullet 35 - 8750 \bullet 0, 5C_{1} > 0$

$$C_{1} < \frac{42875}{\ \ 4375} < 9, 8\$$

$C_{1} < 9, 8$ кезінде жүйе Гурвиц критерийіне сәйкес тұрақты болып табылады.

3. Михайлов критерийі бойынша АРЖ орнықтылығын тексеру

Михайловтың критериі келесідей:

АБЖ тұрақтылығы үшін Михайлов годографының жиілік 0-ден +∞ ге дейін өзгергенде, өзінің қозғалысын оң заттық жартылай осьтен бастап, оң бағытта (сағат тіліне қарсы) айнала отырып, және еш жерде нульге қарамай, кешенді жазықтықта N квадранттардың тізбектерінен өтіп, 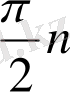бұрышқа бұрылып, n - сипаттамалық теңдеудің тәртібі болуы қажет және жеткілікті.

Жүйенің сипаттамалық теңдеуі:

$a_{3}\ {р\ }^{3} + a_{2}р^{2} + a_{1}р + a_{0} = 0\ \$ $n = 3$

$$8750{р\ }^{3} + {1225р}^{2} + 35р\ + 0, 5C_{1} = 0\$$

$$p \rightarrow \ i\omega$$

$a_{3}\ {(i\omega) \ }^{3} + a_{2}{(i\omega) }^{2} + a_{1}(i\omega) + \ a_{0} = 0\ \$ $n = 3$

$$8750{(i\omega) }^{3} + {1225(i\omega) }^{2} + 35(i\omega) + 0, 5C_{1} = 0\$$

M(ω) : $a_{0}-\ a_{2}\omega^{2} = 0, 5C_{1} - 1225\omega^{2} = 0$

N(ω) : $a_{1}\omega -a_{3}\omega^{3} = \omega\left( a_{1} - \ a_{3}\omega^{2} \right) = \omega\left( 35 - 8750\omega^{2} \right) = 0$

$C_{1} < 9, 8$ тексеру үшін кез келген мәнді орнатамыз

0-ден +∞ ге дейінгі ω жиілік мәнін анықтаймыз

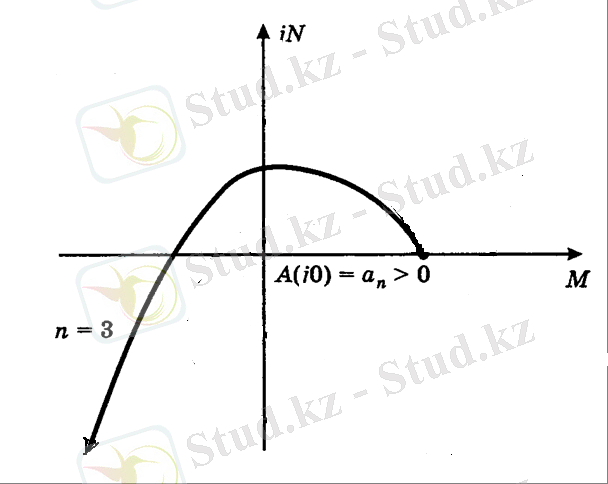
4. Найквист критерийі бойынша АРЖ орнықтылығын тексеру

Найквистің критериі тұйықталған W ( i ω) жүйесінің АФХ бойынша тұйықталған САУ орнықтылығын бағалауға мүмкіндік береді. Егер жиіліктің -∞ < ω < +∞, АФХ өзгеруі кезінде W ( i ω) комплексті жазықтықта ажыратылған жүйенің ( -1, i 0) координаттары бар нүктені қамтымаса, жабық күйінде тұрақты болады.

$${W(p) }_{САУ} = {\ W(p) }_{рег}*\ {W(p) }_{об}$$

$${W(p) }_{об} = {\ W(p) }_{1}*\ {W(p) }_{2}*\ {W(p) }_{3}$$

$$W_{р}(p) = \ - \ C_{1}$$

$${W(p) }_{об}\ = \frac{К_{1}}{T_{1}P + 1}*\frac{К_{2}}{T_{2}P + 1}*\frac{1}{T_{3}P}*( - \ C_{1})$$

$${W(p) }_{САУ} = \frac{К_{1}К_{2}( - \ C_{1}) }{T_{1}{T_{2}T_{3}P}^{3} + (T_{1}T_{3} + T_{2}T_{3}{) P}^{2} + T_{3}P}$$

$$p \rightarrow \ i\omega$$

$$W(iw) \ = \frac{- a_{0}}{- a_{3}iw^{3} - a_{2}w^{2} + a_{1}iw}$$

... жалғасы

Сызықты жүйенің моделі

Автоматты басқару теориясы

Автоматты басқарудың оптимальды жүйелері

Пропорционал-интегралдық (С0, С1) реттегіштің баптау параметрлерінің жазықтығында тұйық автоматты реттеу жүйесінің орнықтылық аймағын тұрғызу

Автоматты басқару жүйесін жобалау

Ылғалды ауаның негізгі параметрлері

Конвейер қондырғысының сипаттамасы

Тұрақты тоқтың двигатель валының айналу жилігінің автоматты реттеу жүйесінің (арж) анализімен тиімделуі

ТЕХНИКАЛЫҚ ЖҮЙЕЛЕРДІ АВТОМАТТАНДЫРУ

Автоматты реттеуіштер

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс