Пропорционал-интегралдық (С0, С1) реттегіштің баптау параметрлерінің жазықтығында тұйық автоматты реттеу жүйесінің орнықтылық аймағын тұрғызу

Ғ. Даукеев атындағы «АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»

КОММЕРЦИЯЛЫҚ ЕМЕС АКЦИОНЕРЛІК ҚОҒАМ

ӨНЕРКӘСІПТІК ЖЫЛУ ТЕХНОЛОГИЯ КАФЕДРАСЫ

№3 ЕСЕПТЕУ-ГРАФИКАЛЫҚ ЖҰМЫСЫ

Пән: «Жылутехнологиясындағы жылутехнологиялық процестерді АБТ және АБЖ

Тақырыбы: Пропорционал-интегралдық (С ₀ , С ₁ ) реттегіштің баптау параметрлерінің жазықтығында тұйық автоматты реттеу жүйесінің орнықтылық аймағын тұрғызу.

Мамандық: 5В071700 - Жылуэнергетика

Топ: ТЭ(ПТЭ) к-17-2

Сынақ кітапшасы: № 171175

Орындаған: Арман Айнур

Қабылдаған: доц. Джаманкулова Н. О

«» 2020ж.

(бағасы) (қолы)

Алматы 2020

Кіріспе

Автоматтандырылған басқару жүйесі (АБЖ) - белгіленген мақсатқа сәйкес, күрделі үдерісті (нысанды) тиімді басқаруды қамтамасыз ететін математикалық әдістердің, техникалық құралдардың (ЭЕМ, байланыс құралдары, ақпаратты бейнелеу құрылғылары және т. б. ) және ұйымдастыру кешендерінің жиынтығы. АБЖ негізден және қызметтік бөліктен тұрады. Оның негізіне ақпараттық, техникалық және математикалық жасақтама кіреді. Қызметтік бөлікке басқарудың нақты функцияларын автоматтан-дыратын, өзара байланысты бағдарламалардың жиынтығын жатқызамыз. АБЖ маңызды міндеті - еңбек өнімділігін арттыру және басқару үдерістерін жоспарлау мен реттеу әдістерін жетілдіру негізінде нысанды (өндірістік, әкімшілік және т. б. ) басқару тиімділігін жоғарылату.

2. 4. 2 Реттеу жүйесінің орнықтылық қорын және тездігін өтпелі сипаттамасы бойынша анықтау әдісін түсіндіріңіз.

Кел келген автоматты реттеу жүйелердің маңызды қасиеттерінің бірі оның орнықтылығы болып табылады. Автоматты реттеу жүйесі жұмысқа қабілеттілігін сақтау үшін жүйе орнықты болуы қажет. Сондықтан орнықтылықты талдау басқару теориясының негізгі тапсырмаларының бірі болып табылады.

Егер автоматты реттеу жүйесі сыртқы күштер әсереткеннен кейін озінің бастапқы (тең) күйіне қайтып келсе орнықты жүйе болады. Егер жүйеге сыртқы күштер әсер еткеннен соң, өзінің күйіне қайта келмесе, онда жүйе орнықсыз болады.

Кез келген автоматты реттеу жүйесі орнықты болу керек. Бұл барлық реттеу жүйелеріне негізгі талап болады.

Жүйелерді үш типке бөледі:

а) орнықты жүйелер -сыртқы әсерлерді алып тастаған соң өзінің бастапқы күйіне қайта келетін жүйе;

б) нейтралды жүйелер (бейтарап) -сыртқы әсерлерді алып тастаған соң өзінің бастапқы күйінен басқа тепе-теңдік жағдайына оралады;

в) орнықсыз жүйелер -сыртқы әсерлерді алып тастаған соң өзінің бастапқы күйінен келмейтін жүйе.

Тепе-теңдік орнықтылығын байқау үшін тереңдікте жатқан шарды алуға болады. Орнықты күйінен шарды ауытқыту кезінде ол тура сол орнына (үйкеліс күші болмағанда) немесе орнықтылықтың кейбір соңғы аймағына (үйкеліс күші болғанда) келуге ұмтылады. Осындай шардың күйіорнықты (1сурет) болады. A ₀ -нүктесіне сәйкес келетін тепе-теңдіктің ауытқымайтын жағдайында және A ₂ -нүктесіне сәйкес келетін тепе-теңдіктен ауытқитын жағдайдағы түсінікті енгізейік. Сыртқы күш әсер ету тоқтаған соң шар A ₀ немесе A ₁ нүктелеріне келеді. Орнықтылық шарты: егертепе-теңдіктіңқарсы әсер күйінен тепе-теңдіктіңқарсы әсерсіз күй қамтыған кейбір аймақтарына өтсе, орнықты болады.

1 сурет-Жүйенің орнықтылығын анықтау

Жалпы жағдайда, сызықты емес жүйені қарастыра отыра, орнықтылықтың «аз», «көп», «толық»ұғымдары енеді.

Жүйе «аз» орнықты болады, егер орнықтылықаймақтың болуынан ғана құрылса, бірақ қандай да бір оның шегін анықтамайды.

Жүйе «көп»орнықты, егер орнықтылық аймағының шегі анықталса, яғни бастапқы ауытқу аймағы анықталады. Сондай-ақ жүйе бастапқы күйіне келеді және нақты бастапқы ауытқулар осы аймаққа сәйкес келетіні анықталады.

Жүйе «толық»орнықты, егер жүйе кез келген бастапқы ауытқулар кезінде қайта басқапқы күйіне келсе.

Орнықтылық шарттарын алу үшін дифференциал теңдеулерді пайдалану қолайлы.

Автоматты басқарудың сызықты жүйесі жалпы жағдайда тұрақты коэффициентті сызықты дифференциал теңдеулермен анықталады:

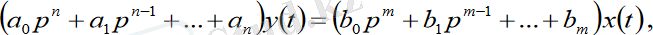
Мұндағы a ₀ , a ₁ , …a _n және b ₀ , b ₁ , …b _m -тұрақты коэффициенттер.

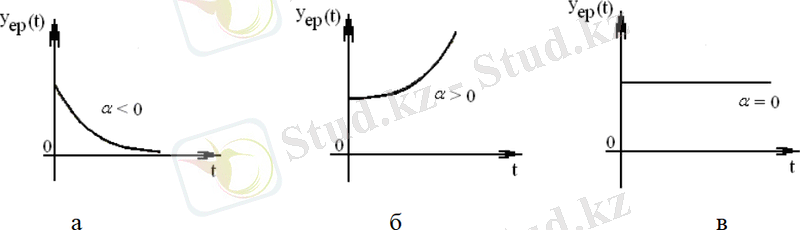
2 сурет-Нақты түбір кезіндегі сипаттамалық теңдеудің еркін құраушылар түрі

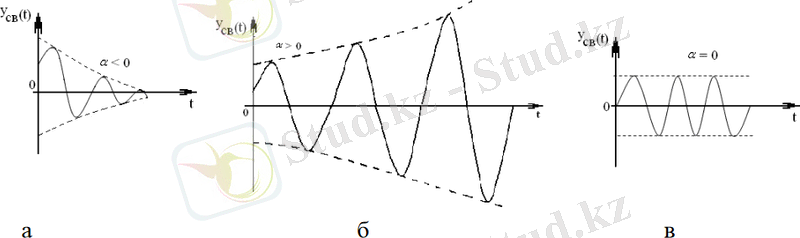
3 сурет - Сипаттамалық теңдеудің комплексті-түйіндес кезіндегі еркін құраушылардың түрі

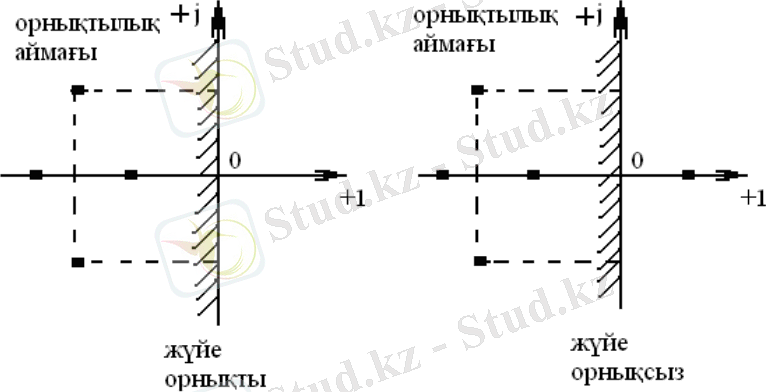
4 сурет-Комплексті жазықтықта сипаттамалық теңдеулер түбірлерінің орналасуы

2. 4. 7 Вышнеградский диаграммасын реттеу жүйесінің орнықтылық қорын және тездігін зерттеу үшін қолдану әдісін түсіндіру.

Вышнеградский Диаграммасы

3-ші ретті жүйелердің орнықтылығын талдау үшін, сондай-ақ құру ережелері 1876 жылы тұжырымдалған Жоғарыградтық диаграмма қолданылуы мүмкін. Бұл Диаграмма бойынша қарастырылып отырған жүйенің орнықтылығы туралы ғана емес, сонымен қатар сипаттамалық теңдеудің тамырының түрін, демек, өтпелі процестің сипатын анықтауға болады.

3-ретті жүйенің сипаттамалық теңдеуін қарастырайық:

а ₀ р ³ + а ₁ р ² + а ₂ р + а ₃ = 0

Д

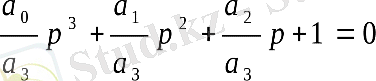
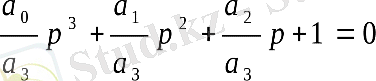
Бұл теңдеуді қалыпты түрге келтіру үшін, оның екі бөлігін а3 бөлеміз

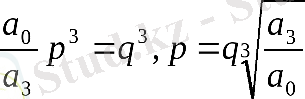
Сонда бастапқы теңдеу көрініс алады: q ³ + Xq ² + Yq + 1 = 0

және белгілеулерді енгіземіз:

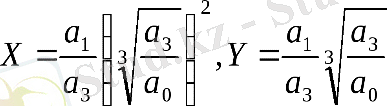
Диаграммада (сурет. 33) координаттарда (Х, Y), сызықтармен сипаттамалық теңдеу түбірлерінің әртүрлі комбинацияларына сәйкес келетін аймақтар бөлінген.

Орнықтылық шегі XY = 1 қисығын анықтайды. Шекаралық қисықтың төменгі жағында және сол жағында орналасқан IV облыста оң заттай бөлігі бар кешенді тамырлардың жұбы бар.

С нүктесінде, мұнда Х =Y = 3, сипаттамалық нормаланған теңдеу (q + 1) 3 = 0 түрін қабылдайды. Демек, бұл нүктеде барлық үш түбір тең: q1 = q2 = q3 = -1

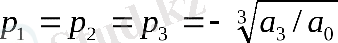
Жалпы жағдайда тұрақтылық аймағында екі нұсқа болуы мүмкін:

1) барлық үш түбірлі;

2) бір түбір заттай және екі кешенді.

I және II облыстарда бір заттай түбірі және екі комплексті бар, өтпелі процесс суретте көрсетілген формаларға сәйкес болады. 34 а, б.

I облыстары экспонентті тез өшеді, және өтпелі процесс негізінен тербеліс құраушысымен анықталатын болады. Бұл тербеліс процестері аймағы болады. II облыста, керісінше, тербелмелі құрамдауыш тез өшеді. Бұл монотонды процестер аймағы болады.

№ 3 есеп

Пропорционал-интегралдық (С ₀ , С ₁ ) реттегіштің баптау параметр-лерінің жазықтығында 3-суретте келтірілген тұйық автоматты реттеу жүйе-сінің орнықтылық аймағын тұрғызыңыз.

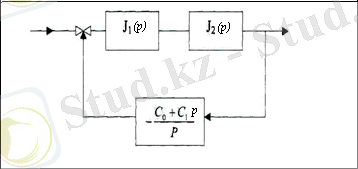
3 сурет

1. K(p) об× K(p) р=1 K(p) об×K(p) р- 1=0 (1)
2. K1(P) =0, 510p+1K_{1}(P) = \frac{0, 5}{10p + 1}

$K_{2}(P) = \frac{0, 5}{10p}$

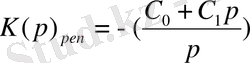
Объект пен реттегіштің мәндерін қойамыз:

$\frac{0, 5}{15p} \bullet \frac{0, 5}{20p} \bullet \left( \frac{- C_{0} - C_{1}p}{p} \right) - 1 = 0$

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс