Параллелепипед, призмалар мен пирамидалардың көлемі және бүйір бетінің теоремалары мен дәлелдері


Дененің көлемі. Параллелепипедтің, призманың көлемі.
Призма деп әр түрлі жазықтықтарда жататын және параллель көшіргенде бір-біріне дәл келіп беттесетін екі көпбұрыштан және көпбұрыштардың сәйкес нүктелерін қосатын барлық кесінділерден тұратын кеңістіктегі денені айтамыз.
Т е о р е м а: Тік призманың бүйір бетінің ауданы табанының периметрін призманың биіктігіне көбейткенге тең.
Т е о р е м а: Кез келген призманың көлемі табан ауданы мен биіктігінің көбейтіндісіне тең болады.
Д ә л е л д е у і. Алдымен үшбұрышты призманы қарастырамыз. Оны параллелепипедке дейін толықтырамыз. О нүктесі параллелепипедтің симметрия центрі болып табылады. Сондықтан толықтырылған призма бастапқы призмамен О нүктесіне қарағанда симметриялы, ендеше, көлемі бастапқы призманың көлеміне тең болады. Сонымен, салынған параллелепипедтің көлемі берілген призманың екі еселенген көбейтіндісіне тең.
Параллелепипедтің көлемі табан ауданын биіктігіне көбейткенге тең. Оның табан ауданы АВС үшбұрышының екі еселенген ауданына тең, ал биіктігі бастапқы призманың биіктігіне тең. Бұдан бастапқы призманың көлемі табан ауданын биіктігіне көбейткенге тең болады деген қорытынды шығарамыз.
Енді еркімізше алынған призманы қарастырайық. Оның табанын үшбұрыштарға бөліктейміз. АВС - осы үшбұрыштардың бірі болсын. АВС үшбұрыштың еркімізше алынған Х нүктесінен бүйір қырларға параллель түзу жүргізейік. а х - осы түзудің призмаға тиісті кесіндісі болсын. Х нүктесі АВС үшбұрышты сызып шыққанда, а х кесінділері үшбұрышты призманы толықтырады. Әрбір АВС үшбұрыш үшін осындай пизманы сала отырып, біз берілген призманы үшбұрышты призмаларға бөліктейміз. Осы призмалардың барлығының биіктігі бірдей, ол бастапқы призманың биіктігіне тең.
Берілген призманың көлемі оны құрайтын үшбұрышты призмалардың көлемдерінің қосындысына тең. Дәлелденген бойынша үшбұрышты призманың көлемі табан ауданын биіктігіне көбейткенге тең болып шығады:
V = S 1 H + S 2 H +… +S n H = (S 1 + S 2 +…+S n ) H,
мұндағы S 1 , S 2 , …, S n - призманың табаны бөлінген үшбұрыштардың аудандары, ал Н - призманың биіктігі. Үшбұрыштар аудандарының қосындысы берілген призма табанының ауданына тең. Сондықтан
V = SH.
Пирамидананың, қиық пирамидананың көлемі
Дұрыс пирамида. Егер пирамиданың табаны дұрыс көпбұрыш болса, ол дұрыс пирамида деп, ал пирамиданың төбесін табан центрімен қосатын кесінді оның биіктігі деп аталады.
Т е о р е м а. Дұрыс пирамиданың бүйір бетінің ауданы табаны периметрінің апофемасына көбейтіндісінің жартысына тең.
Қиық пирамида. Еркімізше РА 1 А 2 . . . А n пирамидасын алып, оның α табан жазықтығына параллель және бүйір қырларын В 1 , В 2 , . . . , В n нүктелерінде қиятын β қиюшы жазықтығын жүргізейік.
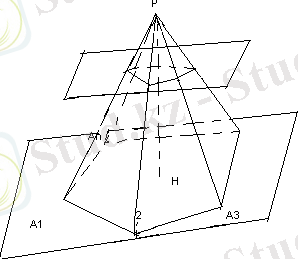
Т е о р е м а. Дұрыс қиық пирамиданың бүйір бетінің ауданы табандарының периметрлері қосындысының жартысы мен апофемасының көбейтіндісіне тең.
Т е о р е м а. Пирамиданың көлемі табанының ауданы мен биіктігінің үштен бір көбейтіндісіне тең.
Д ә л е л д е у і. Теореманы әуелі үшбұрышты пирамида үшін, одан кейін кез келген пирамида үшін дәлелдейміз.
1. Табанының ауданы S, биіктігі h, ал көлемі V болатын ОАВС үшбұрышты пирамиданы қарастырамыз. Ох осін жүргізіп, пирамиданы Ох осіне перпендикуляр жазықтықпен, демек, табан, жазықтығына параллель жазықтықпен қиғандағы А 1 В 1 С 1 қимасын қарастырайық.
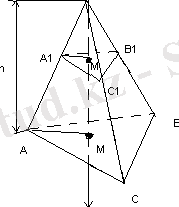
Бұл жазықтықтың Ох осімен қиылысу М
1
нүктесінің абсциссасын х деп, ал қимасының ауданын S(x) арқылы белгілейік. S(x) функциясын S, һ және х арқылы өрнектейміз. А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас. Шынында да, А
1
В
1
׀׀
АВ, сондықтан ΔОАВ ~ ΔОА
1
В
1
. Олай болса,
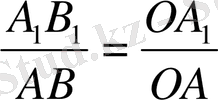 . Тікбұрышты ОА
1
М
1
мен ОАМ үшбұрыштары да ұқсас. Сондықтан
. Тікбұрышты ОА
1
М
1
мен ОАМ үшбұрыштары да ұқсас. Сондықтан
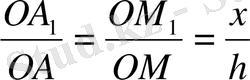 . Сонымен:
. Сонымен:
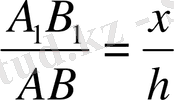 . Осы сияқты
. Осы сияқты
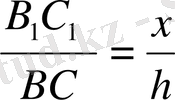 және
және
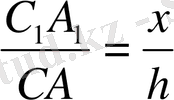 дәлелденеді. Сонымен, А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас,
дәлелденеді. Сонымен, А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас,
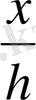 ұқсастық коэффициенті. Олай болса,
ұқсастық коэффициенті. Олай болса,
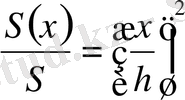 , бұдан S(x) =
, бұдан S(x) =
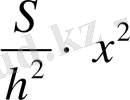 . a = 0, b = h болғанда дененің көлемін есептеудің негізгі формуласын пайдалансақ,
. a = 0, b = h болғанда дененің көлемін есептеудің негізгі формуласын пайдалансақ,
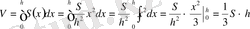 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz