Параллелепипедтің қасиеттері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Параллелепипед.

Егер призманың табаны параллелограмм болса, онда ол параллелепипед деп аталады. Параллелепипедтің барлық жақтары - параллелограмдар.

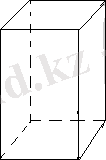
8, а - суретте - көлбеу параллелепипед, ал 8, б - суретте тік параллелепипед кескінделген.

Параллелепипедтің ортақ төбелері болмайтын жақтары қарама-қарсы жатқан жақтары деп аталады.

Теорема 2. Параллелепипедтің қарама - қарсы жатқан жақтары параллель және тең болады.

Параллелепипедтің центрлік симметриясы.

Теорема 3 . Параллелепипедтің диагональдары бір нүктеде қиылысады және қиылысу нүктесінде қақ бөлінеді.

3-ші теоремадан параллелепипедтің диагональдарының қиылысу нүктесі оның симметрия центрі болып табылатындығы шығады.

Тік бұрышты параллелепипед.

Табаны тік төртбұрыш болатын тік параллелепипед тік бұрышты параллелепипед деп аталады. Тік бұрышты параллелепипедтың барлық жақтары- тік төртбұрыштар. Барлық қырлары тең болатын тік бұрышты параллелепипед куб деп аталады. Тік бұрышты параллелепипедтің параллель емес қырларының ұзындықтары оның сызықтық өлшемдері деп аталады. Тік бұрышты параллелепипедтің сызықтық үш өлшемі бар.

Теорема 4. Тік бұрышты параллелепипедтің кез келген диагоналының квадраты оның сызықтық үш өлшемінің квадратының қосындысына тең болады.

Тік бұрышты параллелепипедтің симметриясы.

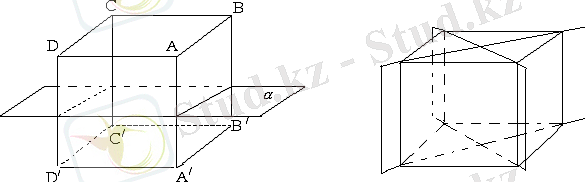Тік бұрышты параллелепипедтің, барлық параллелепипедтер сияқты, ол - диагональдарының қиылысу нүктесі. Сондай - ақ оның симметрия центрі арқылы жақтарына параллель өтетін үш симметрия жазықтығы бар. 9- суретте осындай жазықтықтардың біреулері көрсетілген. Ол параллелепипедтің параллель төрт қырының симметриялы нүктелері болып табылады.

Егер параллелепипедтің барлық сызықтық өлшердері әр түрлі болса, онда оның аталғанынан өзге симметрия жазықтықтары болмайды.

Егер параллелепипедтің екі сызықтық өлшемі тең болса, онда оны тағы екі симметрия жазықтығы бар деген сөз. Бұл 10-суретте көрсетілген диагональдың қималар жазықтығы.

Егер параллелепипедтің барлық қырлары тең, яғни ол куб болса, онда оның кез келген диагональдық қимасы симметрия жазықтығы болып табылады. Сонымен кубтың тоғыз симметрия жазықтығы бар.

Призма.

Призма деп әр түрлі жақтарда жататын және паралелль көшіргенде бір -біріне дәл келіп беттесетін екі көпбұрыштан және осы көпбұшыштың сәйкес нүктелерін қосатын барлық кесінділерден тұратын көпжақты атайды (3-сурет) . Көпбұрыштар - призманың табандары , ал сәйкес төбелерді қосатын кесінділер призманың бүйір қырлары деп аталады.

Параллель көшіру дегеніміз қозғалыс, олай болса , призманың табандары тең болады.

Параллель көшіргенде жазықтық паралелль жазықтыққа (немесе өзіне - өзі) ауысады, олай болса, призманың табандары параллель жазықтықтарда жатады. Параллель көшіргенде нүктелер параллель (немесе дәл беттесетін) түзулердің бойымен бірдей қашықтыққа жылжитындықтан, призманың бүйір қырлары параллель және тең болады.

Призманың беті табандары мен бүйір бетінен құралады. Бүйір беті параллелограмдар болып келеді. Осы параллелограмның әрқайсысының екі қабырғасы - табандарының сәйкес қабырғалары, ал қалған екеуі көршілес бүйір қырлары болып табылады.

Призманың биіктігі деп оның табандарының арақашықтығын айтады. Призманың бір жағына тиісті емес екі нүктесін қосатын кесіндіні призманың диагоналы деп аталады.

Егер призманың табаны п - бұрышы болса, онда оны п - бұрышты призма деп аталады.

Біз алғашқы уақытта тек табандары д±рыс көпбұрыш болып келген призмаларды қарастырамыз. Мұндай призмалар дөњес көпжақ болып табылады.

3-суретте бес бұрышты призма көрсетілген. Оның табандары А ₁ А ₂ . . . А ₅ , 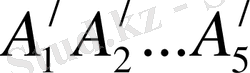бесбұрыштары ХХ ^/ - табандарының сәйкес нүктелерін қосатын кесінді. Призманың бүйір қырлары - 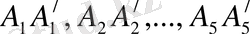. Призманың бүйір жақтары - 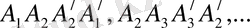параллелограмдары.

Призманы кескіндеу және оның қимасын салу.

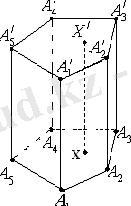
Параллель проекциялаудың ережесіне сәйкес призманың кескінін төмендегідей етіп саламыз. Ең алдымен табандарының бірі Р- ны салады (4- сурет) . Ол қандай да бір жазық көпбұрыш. Сонан соң Р көпбұрышының төбелерінен ұзындықтары бірдей паралелль кесінділер түрінде призманың бүйір қырлары жүргізіледі. Осы кесінділердің ұштары өзара қосылса да, призманың екінші табанын шығарып алады. Көрінбейтін қырларды үзік сызықтармен жүргізеді.

Призманың бүйір қырларына паралелль жазықтықтармен қиғанда шығатын қималар параллелограмдар болып табылады. Бұл қималар бір жаққа тиісті емес екі бүйір қыры арқылы өтетін жазықтықтармен қиғанда шығады (5- сурет) .

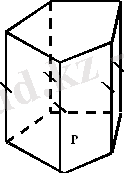
Іс жүзінде атап айтқанда есеп шығарғанда, көбінесе, призманың бір табанының жазықтығында берілген g түзуі арқылы өтетін жазықтықпен қиғанда пайда болатын призма қимасын салуға тура келеді. Мұндай түзуді қиюшы жазықтықтың табан жазықтығындағы ізі деп аталады. Призманың қимасын салу үшін қиюшы жазықтықтың призма жақтарымен қиылысатын кесінділерін салу жеткілікті. Призманың бетінде жатқан және қимаға тиісті қандай да бір А нүктесі белгілі болғанда осындай қиманы қалай салатынын көрсетейік. (6- сурет) .

Егер берілген А нүктесі призманың екінші табанына тиісті болса, онда оның қиюшы жазықтықпен қиылысуы g ізіне паралелль және берілген А нүктесін қамтитын ВС кесіндісі болады (6. а - сурет)

Егер А нүктесі призманың бүйір жағына тиісті болса, онда осы жақтың қиюшы жазықтықпен қиғандағы қимасын 6. б - суретте көрсетілгендей етіп салады.

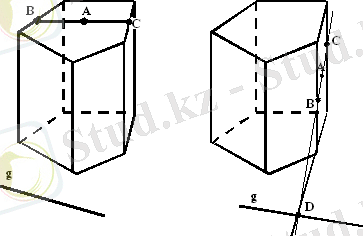
Атап айтсақ: ең алдымен жақтың жазықтығы мен алдын ала берілген g ізі қиылысатын D нүктесін салып алады. Содан соң А және D нүктелері арқылы түзу жүргізіледі. Қарастырып отырған жақтың бетінде жатқан АD түзуінің ВС кесіндісі - осы жақпен қиюшы жазықтықтың қиылысуы. Егер А нүктесін қамтитын жақ g ізіне параллель болса, онда қиюшы жазықтық бұл жақты А нүктесі арқылы өтетін және g түзуіне параллель ВС кесіндісінің бойымен қияды.

ВС кесіндісінің ұштары көршілес жақтарға да тиісті болады. Сондықтан жоғарыда аталған тәсілмен осы жақтардың өзіміздің қиюшы жазықтығымызбен қиылысуын салуға болады, т. с. с.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.