Пирамидалар және олардың қималары: анықтамалар, қиық пирамида және көлем мен бет аудандарының теоремалары


Пирамида.
Пирамида дегеніміз жазық көпбұрыштан - пирамиданың табанынан, табан жазықтығында жатпайтын нүктеден - пирамиданың төбесінен және пирамиданың төбесін табанының нүктелерімен қосатын барлық кесінділарден құралған көпжақ (1 -сурет) . Пирамиданың төбесін табанының төбелерімен қосатын кесінділер пирамиданың бүйір қырлары деп аталады.
Пирамиданың беті табаны мен бүйір жақтарынан тұрады. Әрбір бүйір жағы - үшбұрыш. Оның бір төбесі пирамиданың да төбесі, ал қарама - қарсы жатқан қабырғасы пирамида табанының қабырғасы болып табылады. Пирамиданың биіктігі деп пирамиданың төбесінен табан жазықтығына түсірілген перпендикулярды атайды.
Егер пирамиданың табаны n - бұрыш болса, онда ол n - бұрышты пирамида деп аталады. Үш бұрышты пирамида тетраэдра деп те аталады.
1 - суретте кескінделген пирамиданың табаны - А
1
А
2
. . . А
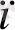 n көпбұрыш, призманың төбесі - S, бүйір ќырлары - SA
1
, SA
2
, …, SA
n
, бүйір жақтары -
n көпбұрыш, призманың төбесі - S, бүйір ќырлары - SA
1
, SA
2
, …, SA
n
, бүйір жақтары -
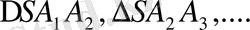
Біз алдағы уақытта табандары дұрыс көпбұрыш болып келген пирамидаларды ғана қарастырамыз. Онда пирамидалар дөңес көпжақтар болып табылады.
 Пирамидаларды және оның жазық қималарын салу.
Пирамидаларды және оның жазық қималарын салу.
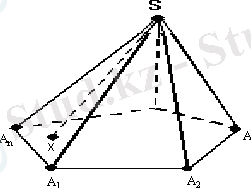
Параллель проекциялау ережесіне сәйкес пирамиданың кескінін төмендегідей салады. Ең алдымен табаны салынады. Бұл қандай да бір жазық көпбұрыш. Содан соң пирамиданың төбесін белгілейді де. Оны бүйір қыры арқылы табанының төбесімен қосады, 2- сурет бес бұрышты пирамиданың кескіні көрсетілген.
Пирамиданы төбесі арқылы өтетін жазықтықтармен қиғанда қималар үшбұрыштар болып келеді (3 - сурет) . Дербес жағдайда, диагональдық қималар үшбұрыштар болады. Бұл - пирамиданың көршілес емес екі бүйір қыры арқылы өтетін жазықтықтармен қиғанда шығатын қималар (4 - сурет) .
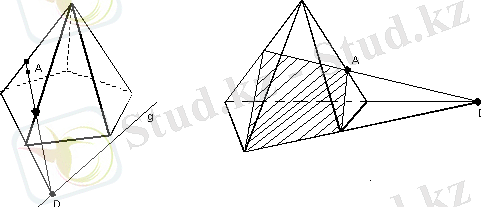
Жазықтықтың пирамиданың табан жазықтығындағы g ізі берілген жағдайда пирамиданың осы жазықтықпен қиғанда шығатын қимасын призманың қимасын салғандай етіп саламыз. Пирамиданың жазықтықпен қиғандаға қимасын салу үшін, оның бүйір жақтарын қиюшы жазықтықпен қиылысуын салу жеткілікті.
Егер g ізге паралелль емес жақтың қимағы тиісті қандай да бір А нүктесі белгілі болса, онда қиюшы жазықтықтың g ізінің осы жақ жазықтығымен қиылысуын - 5-суреттегі D нүктесін салады. D нүктесін А нүктесімен түзу арқылы қосады. Сонда осы түзудің жаққа тиісті кесіндісі осы жақ пен қиюшы жазықтықтың қиылысуы болып шығады. Егер А нүктесі g ізіне паралелль жақта жатса, онда қиюшы жазықтық бұл жақты g түзуіне параллель кесіндінің бойымен қиып өтеді. Көршілес бүйір жаққа ауысып, оның қиюшы жазықтықпен қиылысуын салады және т. с. с. Нәтижесінде пирамиданың қажет болып отырған қимасы
 шығады.
шығады.
6-суретте төртбұрышты пирамиданың табан қабырғасымен оның бүйір қырларының бірінде жатқан А нүктесі арқылы өтетін жазықтықпен қиғанда қимасы салып көрсетілген.
Пирамиданың барлық жақтары, яғни табаны мен бүйір жақтарының аудандарының қосындысы оның толық бетінің ауданы деп, оның бүйір жақтарының аудандарының қосындысы пирамиданың бүйір бетінің ауданы деп аталады.
S т. б. = S б. б. + S таб. болатыны айқын.
Қиық пирамида .
Теорема 6. Пирамиданы қиып өтетін табанына параллель жазықтық одан ұқсас пирамида қиып өтеді.
Дєлел. Айталық, S - пирамиданың төбесі, А - табанының төбесі және А
/
- қиюшы жазықтықтың AS бүйір қырымен қиылысу нүктесі болсын (7 - сурет) . Пирамиданың S төбесіне қатысты коэффициенті
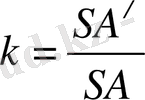 болатын гомотетия түрлендіруіне түсірейік. Бұл гомотетияда табан жазықтығы А
/
нүктесі арқылы өтетін оған параллель жазықтыққа, яғни қиюшы жазықтыққа, олай болса, бүкіл пирамида осы жазықтық қиып түсетін бөлікке ауысады. Гомотетия дегеніміз ұқсас түрлендіру болғандықтан, пирамидадан қиып түсетін бөлік берілген пирамидаға ұқсас пирамида болып табылады. Теорема дәлелденді.
болатын гомотетия түрлендіруіне түсірейік. Бұл гомотетияда табан жазықтығы А
/
нүктесі арқылы өтетін оған параллель жазықтыққа, яғни қиюшы жазықтыққа, олай болса, бүкіл пирамида осы жазықтық қиып түсетін бөлікке ауысады. Гомотетия дегеніміз ұқсас түрлендіру болғандықтан, пирамидадан қиып түсетін бөлік берілген пирамидаға ұқсас пирамида болып табылады. Теорема дәлелденді.
 Бұл теорема бойынша пирамиданың табан жазықтығына параллель және оның бүйір қырларын қиып өтетін жазықтық одан ұқсас пирамила қиып түсіреді. Ал, оның екінші бөлігі көпжақ болып шығады, ол қиық пиармида деп аталады (8-сурет) . Қиық пирамиданың параллель жазықтықтарда жататын жақтары табандары деп аталады; қалған жақтары бүйір жақтары деп аталады. Қиық пирамиданың табандары - ұқсас (дәлірек айтқанда, гомотетиялы) көпбұрыштар, бүйір жақтары трапециялар болып келеді
Бұл теорема бойынша пирамиданың табан жазықтығына параллель және оның бүйір қырларын қиып өтетін жазықтық одан ұқсас пирамила қиып түсіреді. Ал, оның екінші бөлігі көпжақ болып шығады, ол қиық пиармида деп аталады (8-сурет) . Қиық пирамиданың параллель жазықтықтарда жататын жақтары табандары деп аталады; қалған жақтары бүйір жақтары деп аталады. Қиық пирамиданың табандары - ұқсас (дәлірек айтқанда, гомотетиялы) көпбұрыштар, бүйір жақтары трапециялар болып келеді
Қиық пирамиданың бүйір жақтары аудандарының қосындысы қиық пирамиданың бүйір бетінің ауданы деп аталады.
Теорема 7 . Дұрыс қиық пирамиданың бүйір бетінің ауданы табандарының периметрлері қосындысының жартысы мен апофемасының көбейтіндісіне тең.
Бұл теорема дұрыс пирамиданың бүйір бетінің ауданы туралы теорема сияқты дәлелденеді.
Енді пирамиданың көлемін қарастырайық.
Теорема 8. Пирамиданың көлемі табанының ауданы мен биіктігінің үштен бір көбейтіндісіне тең.
Дәлел. Теореманы әуелі үшбұрышты пирамида үшін, одан кейін кез келген пирамида үшін дәлелдейміз.
1. Табанының ауданы S, биіктігі h, ал көлемі V болатын ОАВС үшбұрышты пирамиданы қарастырамыз. Ох осін жүргізіп, пирамиданы Ох осіне перпендикуляр жазықтықпен, демек, табан, жазықтығына параллель жазықтықпен қиғандағы А 1 В 1 С 1 қимасын қарастырайық.
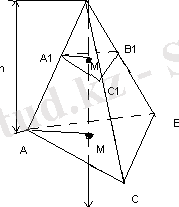 Бұл жазықтықтың Ох осімен қиылысу М
1
нүктесінің абсциссасын х деп, ал қимасының ауданын S(x) арқылы белгілейік. S(x) функциясын S, һ және х арқылы өрнектейміз. А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас. Шынында да, А
1
В
1
׀׀
АВ, сондықтан ΔОАВ ~ ΔОА
1
В
1
. Олай болса,
Бұл жазықтықтың Ох осімен қиылысу М
1
нүктесінің абсциссасын х деп, ал қимасының ауданын S(x) арқылы белгілейік. S(x) функциясын S, һ және х арқылы өрнектейміз. А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас. Шынында да, А
1
В
1
׀׀
АВ, сондықтан ΔОАВ ~ ΔОА
1
В
1
. Олай болса,
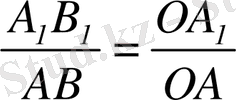 . Тікбұрышты ОА
1
М
1
мен ОАМ үшбұрыштары да ұқсас. Сондықтан
. Тікбұрышты ОА
1
М
1
мен ОАМ үшбұрыштары да ұқсас. Сондықтан
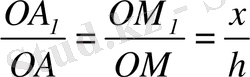 . Сонымен:
. Сонымен:
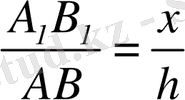 . Осы сияқты
. Осы сияқты
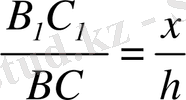 және
және
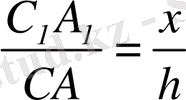 дәлелденеді. Сонымен, А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас,
дәлелденеді. Сонымен, А
1
В
1
С
1
мен АВС үшбұрыштары ұқсас,
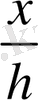 ұқсастық коэффициенті. Олай болса,
ұқсастық коэффициенті. Олай болса,
 , бұдан
, бұдан
S(x) =
 . a = 0, b = h болғанда дененің көлемін есептеудің негізгі формуласын пайдалансақ,
. a = 0, b = h болғанда дененің көлемін есептеудің негізгі формуласын пайдалансақ,
 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz