Вариациялық қатарлар мен олардың статистикалық сипаттамалары: интервалдық талдау және кенорын сынақтарына қолдану


1 ВАРИАЦИЯЛЫҚ ҚАТАРЛАР ЖӘНЕ ОЛАРДЫҢ СТАТИСТИКАЛЫҚ СИПАТТАМАЛАРЫ
1. 1 Вариациялық қатарлар және олардың элементтері
Статистикалық деректер деп сапалық белгілерге ие, бақылау объектілері туралы сандық мәліметтер аталады. (Мысалы, пайдалы компоненттің болуына сынап көру деректері, шоғырдың қуаттылығы туралы, участкі бойынша кенді қазу көлемдері туралы мәліметтер) . Сапалық ортақтыққа ие біртекті бірліктерден тұратын мұндай деректердің жиынтығы статистикалық жиынтық немесе статистикалық ұжым деп аталады.
Статистикалық жиынтықты құрайтын көрсеткіштер шамасы бойынша өзгереді (вариацияланады) . Сондықтан олардың мәндері варианттар (х 1 , х 2 , …х n ) деп аталады, ал барлық жиынтығы- вариациялық қатар .
Жиынтықтың құрамына кіретін жеке бірліктер, оның элементтері немесе ұжымның мүшелері деп аталады, барлық элементтердің саны жиынтықтың көлемі (n) деп аталады.
Әрбір вариант неше рет байқалғанын көрсететін сандар жиіліктер деп аталады және m 1 , m 2 , …, m n арқылы белгіленеді.
Варианттарды өсуші немесе кемуші тәртіпте орналастырып және әрбір варианттың жиілігін көрсетіп, тәртіпке келтірілген вариациялық қатар немесе белгіні бөлуді аламыз.
Вариациялық қатарды интервалды қатар түрінде берген ыңғайлы, онда жиіліктер жеке мәндерге емес, интервалдардың (кластардың) ортасына жатады.
Интервалдың оңтайлы шамасы Стерджесстің формуласымен анықталады.
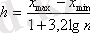 (І. І)
(І. І)
Интервалды вариациялық қатарда әрбір интервалда интервалдардың жоғарғы және төменгі шекарасын айырады. Әрбір интервалға сандық мәндері интервалдың төменгі шекарасынан үлкен және жоғары шекарадан аз немесе тең варианттарды қосады.
Интервалдың жиіліктерін жиынтықтың жалпы көлеміне бөлуден дербестер интервалдардың жиіліктері деп аталады.
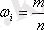 (І. 2)
(І. 2)
Мысал. Полиметалл кеніште 10 забойдан 100 сынама алынған. Сынамалар бойынша металл құрамына химиялық талдаулардың нәтижелері 1. 1. кестеде берілген. Сынау деректерін тәртіпке келтірілген және интервалды вариациялық қатарлар түрінде келтіру талап етіледі.
1. 1 кесте
Кенжар
№
Мет. мазмұны С, %
(х)
кенжар
№
С, %
(х)
кенжар
№
С, %
(х)
кенжар
№
С, %
(х)
кенжар
№
С, %
(х)
1-ші кенжар кенкенкенкенжаркенжар
1
2
3
4
5
6
7
8
9
10
0, 5
0, 55
0, 4
0, 6
0, 4
0, 4
0, 4
0, 4
0, 4
0, 4
3-ші кенжар
1
2
3
4
5
6
7
8
9
30
0, 95
1, 4
1, 8
0, 9
0, 8
0, 5
0, 4
0, 4
0, 4
0, 4
5-ші кенжар
1
2
3
4
5
6
7
8
9
50
0, 85
0, 7
0, 6
0, 6
0, 6
0, 6
0, 6
0, 55
0, 4
0, 5
7-ші кенжар
1
2
3
4
5
6
7
8
9
70
0, 6
0, 6
0, 6
0, 45
0, 6
0, 8
0, 9
0, 9
0, 4
0, 6
9-ші кенжар
1
2
3
4
5
6
7
8
9
90
0, 9
0, 8
0, 6
0, 2
0, 35
0, 7
1, 0
1, 0
0, 4
0, 8
2-ші кенжар
1
2
3
4
5
6
7
8
9
20
0, 75
1, 1
1, 15
0, 8
0, 55
0, 55
0, 4
0, 4
0, 4
0, 4
4-ші кенжар
1
2
3
4
5
6
7
8
9
40
1, 0
1, 2
1, 2
1, 1
0, 85
0, 6
0, 4
0, 4
0, 4
0, 45
6-ші кенжар
1
2
3
4
5
6
7
8
9
60
0, 6
0, 6
0, 55
0, 5
0, 5
0, 7
0, 8
0, 75
0, 6
0, 6
8-ші кенжар
1
2
3
4
5
6
7
8
9
80
0, 6
0, 6
0, 6
0, 4
0, 5
0, 8
1, 0
1, 0
0, 8
0, 65
10-ші кенжар
1
2
3
4
5
6
7
8
9
100
1, 0
0, 65
0, 4
0, 2
0, 4
0, 9
1, 2
1, 1
1, 0
0, 8
Шешім
1 Жиіліктерін көрсетіп, варианттарды өсуші тәртіпте орналастырып, тәртіпке келтірілген вариациялық қатарды құрастырамыз (1. 2. кесте) .
1. 2. Кесте
 варианты
варианты
 жиілігі
жиілігі
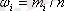
жиілігі
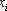 варианты
варианты
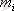 жиілігі
жиілігі
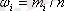
жиілігі
2 (1. 1) формуламен интервалдың оңтайлы шамасын анықтап, интервалды вариациялық қатарды құрастырамыз (1. 3. кесте) .
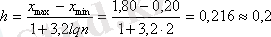
Бірінші интервалдың басына (х mіn -һ/2) тең шаманы қабылдау ұсынылады. Онда, егер а і і-ші интервалдың басы болса, онда
а 1 = х mіn -һ/2; a 2 =a 1 +h; a 3 =a 2 +h және т. б. Интервалдарды құру тәртіп бойынша интервалдың басы х mах тең немесе үлкен болғанша жалғаса береді.
1. 2 Үлестірім қатарының орта статистикалық сипаттамалары
Орта шамалар бақылаудың барлық қатарының өкілдері болады, өйткені оның маңында белгінің байқалатын мәндері шоғырланады. Сапалық бір текті бақылаулар үшін ғана орта мәндерді есептеудің мәні бар. Орта мәндердің белгі тәрізді өлшемділігі бар. Математикалық статистикада орта шамалардың бірнеше түрін айырады; орта арифметикалық, орта геометриялық, орта гармониялық, орта квадратты және т. б.
1. 3 Кесте
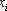 интервал орта мәні
интервал орта мәні
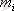 жиілігі
жиілігі
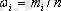
жиілігі
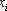 интервал орта мәні
интервал орта мәні
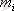 жиілігі
жиілігі
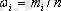
жиілігі
Ортаны есептеу кезінде қандай мақсатты алға қоятындығын білу керек.
Анықтаушы
деген атқа ие болған бұл қасиет ортаның түрін анықтайды. Орта арифметикалықты анықтайтын қасиет былай тұжырымдалады; егер олардың әрбіреуін орта арифметикалықпен ауыстырса, бақылау соммасы өзгермей қалу керек, яғни
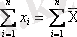 . Осыдан бақылау деректері бойынша орта арифметикалықты есептеу үшін келесі формуланы аламыз.
. Осыдан бақылау деректері бойынша орта арифметикалықты есептеу үшін келесі формуланы аламыз.
(І. 3)
Егер бақылаулар бойынша вариациялық қатар құрылса, онда арифметикалық мына формуламен есептелінді
(І. 4)
Мұнда х 1 , х 2 , …х n - белгі мәнінің жеке бақылаулары;
-бақылаулардың жалпы саны (жиынтық көлем) ;
m 1 , m 2 , …, m n - белгінің сәйкес мәндері үшін бақылаулар жиілігі
Бұл жағдайда ол өлшенген деп аталады.
Практикалық есептерді шешу кезінде ауыстыруда әрбір бақылауда бақылау дәрежелерінің g-x соммасы өзгермей қалатын х
g
ортаны есептеу қажеттілігі пайда болуы мүмкін, яғни
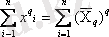
мұнда g- оң немесе теріс сан.
х g орта g- тәртіптің дәрежелік ортасы деп аталады. Осы анықтаушы қасиеттен шыға отырып, бақылау деректері бойынша х g есептеу үшін формула аламыз
(І. 5)
Егер вариациялық қатар болса, g- тәртіптің дәрежелік ортасы өлшенген деп аталады және мына формуламен есептеледі
(І. 6)
Бұл формуладан бірінші тәртіптің дәрежелік ортасы орта арифметикалығы екендігі шығады, яғни Дәрежелік орта минус х -1 бірінші тәртіптің орта гармониялық деп аталады және мына формуламен есептелінеді.
(І. 7)
Екінші тәртіптің дәрежелік ортасы деп орта квадратты деп аталады.
(І. 8)
Х геом орта геометриялық деп х 1 , х 2 , …х n бақылау көбейтіндісінен n дәрежелі түбір аталады.
, (І. 9)
мұнда П- көбейтінді белгісі.
Ортаны қолдану кезінде орта арифметикалықтың мына қасиеттерін ескеру керек:
- орта арифметикалықтан сәйкес жиіліктірге варианттардың ауытқуы көбейтіндісінің соммасы нөлге тең.
(І. 10)
- тұрақты шаманың орта арифметикалығы осы тұрақтыға тең.
- егер барлық варианттарды бір санға азайтса (ұлғайтса), онда арифметикалық сол санға азаяды (ұлғаяды) .
(І. 11)
- егер барлық варианттарды бір санға бір рет азайтса (ұлғайтса), онда орта аривметикалық сонша есе азаяды (ұлғаяды) .
,
(І. 12)
Ортаның қасиеттерін орта арифметикалықты есептеудің оңай тәсілі үшін қолданады, мұнда орта арифметикалықты есептеуді бастапқы вариант
 бойынша емес, бірнеше санға с азайтып есептейді, содан соң
бойынша емес, бірнеше санға с азайтып есептейді, содан соң
 бірнеше санға бөлінген, яғни
бірнеше санға бөлінген, яғни
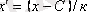 . Өзгертілген қатар үшін орта арифметикалықты
. Өзгертілген қатар үшін орта арифметикалықты
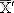 біле отырып, бастапқы қатар үшін орта арифметикалықты есептеу оңай;
біле отырып, бастапқы қатар үшін орта арифметикалықты есептеу оңай;
(І. 13)
Шынында, орта арифметикалықтың төртінші және үшінші қасиетін назарға ала отырып, аламыз
:
Осыдан шығады,
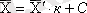
Орта шамалармен қатар вариациялық қатардың суреттеме сипаттамалары ретінде медиана мен мода қолданылады.
Варианттардың тақ саны кезінде медиананы мына формуламен анықтайды:
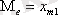 ,
,
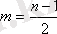 (І. 14)
(І. 14)
варианттардың жұп саны кезінде
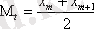 ,
,
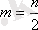 (І. 15)
(І. 15)
Егер вариациялық қатар, интервалды түрде болса, медиананы анықтау кезінде медиана бар интервалды табады, бұл үшін жинақталған жиіліктің нақты вариантты қолданылады. Жинақталған жиілігін осы варианттың жиілігімен берілгеннің алдында болатын варианттардың барлық жиіліктерін қосумен алады. Қосуды өспелі және кемімелі тәртіппен алуға болады.
Медианалы интервал жинақталған жиілік жиынтықтың барлық көлемінің жартысынан асатын болады.
Интервалдардың ішәндегі тығыздықтың тұрақтылығы кезінде медиананың мәнін мына формуламен анықтайды:
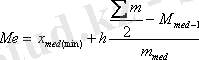 (1. 16)
(1. 16)
мұнда x med(mіn) - медианалы интервалдың төменгі шекарасы;
h - интервалдың шамасы:
M med-1 - медиананың алдында болатын, интервалдың жинақталған жиілігі;
m med - медианалы интервалдың жиілігі.
Мода деп үлестірімнің ең көп тығыздығына сай келетін, ең жиі кездесетін вариант аталады.
Дискретті вариациялық қатарда модаға ең көп жиіліктегі вариант сәйкес келеді. Сондықтан дискретті үлестірімнің модасын табу қандай да бір есептеуді қажет етпейді.
Интервалды вариациялық қатарда модальды интервалды ең көп жиілік (интервалдар тең болғанда) немесе ең көп тығыздық бойынша (интервалдар тең болмағанда) анықтайды.
Моданы мына формуламен есептейді:
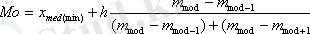 (1. 17)
(1. 17)
мұнда x mod(mіn) - модальды интервалдың төменгі шекарасы:
m mod - модальды интервалдың жиілігі.
Медиана мен моданы үлестірім қатарының симметриялығын жалпы бағалау үшін қолданады. Симметриялы вариациялық қатарлардың ерекшелігі үш орта статистикалық сипаттамалардың теңдігі болып табылады.
Вариация көрсеткіштері . Орта мәндер вариациялық қатарды бір санмен сипаттай отрырып, белгінің байқалатын мәндерінің өзгеруін, вариациясын бейнелейді. Вариацияның қарапайым көрсеткіші ең көп және ең аз варианттар арасындағы айырымға тең вариациялық құлаш (R В ) болып табылады, яғни
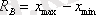 (І. 18)
(І. 18)
Вариациялық құлаш-вариацияның тым жуық көрсеткіші. Орта мәндер маңындағы бақылауларды тарату шаралары үлкен қызығушылық тудырады.
Варианттардың орта арифметикалықтан ауытқуы, яғни
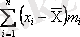 , орта арифметикалықтың жанында варияцияны сипаттай алмайды.
, орта арифметикалықтың жанында варияцияны сипаттай алмайды.
Орта арифметикалықтың бірінші қасиеттің күшіне қарай бұл сомма нөлге тең. Сондықтан айырымдарда
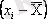 олардың абсолютті шамалары немесе олардың квадраттары алынады. Осыған сәйкес вариацияның әртүрлі көрсеткіштерін алады.
олардың абсолютті шамалары немесе олардың квадраттары алынады. Осыған сәйкес вариацияның әртүрлі көрсеткіштерін алады.
Орта линиялық (сызықтық) ауытқу d деп варианттардың орта арифметикалықтан ауытқуларының абсолютті шамаларының орта арифметикалығы аталады;
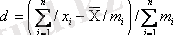 (І. 19)
(І. 19)
Дисперсия δ 2 орта арифметикалықтан варианттар ауытқу квадраттарының орта арифметикалық квадраттары аталады:
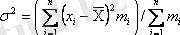 (І. 20)
(І. 20)
Таралу (шашырау) шарасы белгінің мәндері сияқты бірліктерде беріледі, сондықтан дисперсия орнына вариация көрсеткіші ретінде көбінесе дисперсиядан квадраттың түбірі қолдаенылады. Дисперсиядан квадраттың түбірінің арифметикалық мәндері орта квадратты ауытқу немесе стандарт деп аталады:
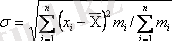 (І. 21)
(І. 21)
Дисперсия орта арифметикалық жанында белгі мәндерін тарату (шашырату) көрсеткіші ретінде артық көрінеді, өйткені ол минимальдық мәнге ие. Басқа сөзбен айтқанда, дисперсия х ерекше, кез келген тұрақты шамадан варианттардың ауытқулар квадраттарының орта арифметикалығынан аз, яғни
, егер
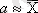
Дисперсия қасиеттері.
1 Тұрақты шаманың дисперсиясы нөлге тең.
2 Егер барлық варианттарды бір санға С азайтса (ұлғайтса), онда дисперсия өзгермейді:
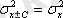 (І. 22)
(І. 22)
3 Егер барлық варианттарды К есе азайтса (ұлғайтса), 4 орташа арифметикалықтың қасиетіне сәйкес өзгертілген вариациялық қатар үшін орта х/к тең, сәйкесінше, оның дисперсиясы
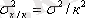 ,
,
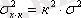 (І. 23)
(І. 23)
4 Егер бақылаулар қатары К бақылау топтарынан қосылса, онда барлық қатардың (δ 2 ) дисперсиясы ішкі топ және топ арасындағы дисперсияның соммасына тең, яғни
мұнда
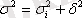 , яғни
, яғни
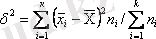 , (І. 24)
, (І. 24)
егер бір қатар бақылауларды К топтарға бөлсе, топ аралық дисперсия (δ 2 ) деп бақылаулардың барлық қатарының ортасынан (х) топтық ортаның (х) ауытқулар квадраттарының орта арифметикалығы аталады, мұнда салмақтар топтардың көлемдері (n і ) болады, ал топтық дисперсиялардың немесе ішкі топтық дисперсияның (δ 2 і ) ортасы деп топтық дисперсиялардың орта арифметикалығы (δ 2 і ) аталады, салмақтар топтардың көлемдері болады (n і ) ;
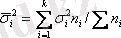 . (І. 25)
. (І. 25)
Есептеулерде көбінесе келесі теореманы қолданады; Дисперсия варианттар квадраттарының орта арифметикалығы мен орта арифметикалық квадрат арасындағы айырмаға тең, яғни
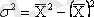 , (І. 26)
, (І. 26)
мұнда
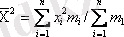 .
.
Инженерлік есептеулерде қолайсыз есептеулерді болдырмау үшін дисперсияны бастапқы варианттар х бойынша емес, бірнеше санға азайтылған С, одан соң К кейбір санға бөлінгенмен есептейді, яғни варианттар үшін
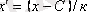 .
.
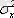 біле отырып (өзгертілген қатар үшін дисперсия), бастапқы қатар үшін δ
2
дисперсиясые есептеу оңай;
біле отырып (өзгертілген қатар үшін дисперсия), бастапқы қатар үшін δ
2
дисперсиясые есептеу оңай;
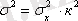 (І. 27)
(І. 27)
Шынында, дисперсияның үшінші және екінші қасиетін назарға ала отырып, аламыз
.
Бұдан шығады
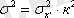
(1. 27) формуланы көбінесе басқа түрде жазады.
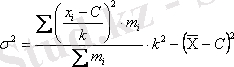 . (І. 28)
. (І. 28)
Одан әрі есептерді шешу кезінде орта арифметикалық пен дисперсияның көрсетілген қасиеттерін пайдаланатын боламыз.
Белгінің варияция дәрежесінің сипаттамасы үшін салыстырмалы көрсеткіш- вариация коэффициентін қолданады;
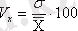 (І. 29)
(І. 29)
Вариация коэффициентін есептеп шығару сенімділігін бағалау V х . Оның қатесі салыстыру жолымен жүргізіледі:
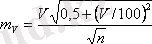 . (І. 30)
. (І. 30)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz