Логарифмдер: анықтама, негізгі қасиеттер және қолданбалы есептер


Логарифмдер. Олардың қасиеттері
Дәрежелерді оқығанда пайда болатын негізгі есептерді қарастырайық.
1.
 мен
мен
 нақты сандары берілген.
нақты сандары берілген.
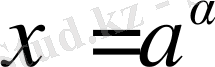 болатындай нақты
х
санын табу керек. Бұл нақты санды дәрежеге шығару болып табылады. Бұл есептің кез-келген
болатындай нақты
х
санын табу керек. Бұл нақты санды дәрежеге шығару болып табылады. Бұл есептің кез-келген
 оң саны мен кез-келген
оң саны мен кез-келген
 нақты саны үшін шешімі бар. Егер
нақты саны үшін шешімі бар. Егер
 және
және
 болса, онда
х
= 0.
болса, онда
х
= 0.
 <0 болғандағы есепті мұнда қарастырмаймыз.
<0 болғандағы есепті мұнда қарастырмаймыз.
2. b саны мен α нақты сандары берілген.
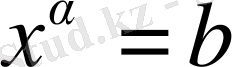 болатындай
х
нақты санын табу керек. Егер b- кез-келген оң сан, ал α- нольден ерекше нақты сан болса, бұл есеп жаңағы есепке келтіріледі, онда жауабы
болатындай
х
нақты санын табу керек. Егер b- кез-келген оң сан, ал α- нольден ерекше нақты сан болса, бұл есеп жаңағы есепке келтіріледі, онда жауабы
 болады. Расында,
болады. Расында,
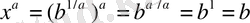 . Егер
. Егер
 және
және
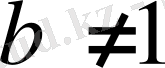 болса, онда есептің шешімі жоқ.
болса, онда есептің шешімі жоқ.
 жағдайын қарастырмаймыз.
жағдайын қарастырмаймыз.
3.
 мен b нақты сандары берілген.
мен b нақты сандары берілген.
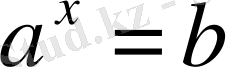 болатындай
х
нақты санын табу керек. Бұл есепті тек оң нақты
болатындай
х
нақты санын табу керек. Бұл есепті тек оң нақты
 мен b сандары үшін ғана қарастырамыз. Егер
a
=1 және
мен b сандары үшін ғана қарастырамыз. Егер
a
=1 және
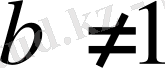 болса, онда есептің шешімі жоқ.
болса, онда есептің шешімі жоқ.
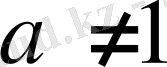 жағдайын қарастырайық.
жағдайын қарастырайық.
1-теорема.
a>0, (
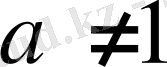 ) және b>0 болатындай кез келген a мен b нақты сандарының пары үшін
) және b>0 болатындай кез келген a мен b нақты сандарының пары үшін
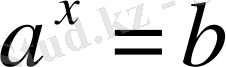 теңдігі орындалатындай нақты х саны бар болады. Және ол жалғыз ғана болады.
теңдігі орындалатындай нақты х саны бар болады. Және ол жалғыз ғана болады.
Осындай х санының бар болуын мұнда дәлелдемейміз. Ол жалғыз ғана болатынын дәлелдейік.
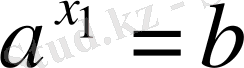 және
және
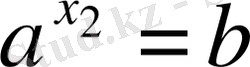 болатындай х
1
және х
2
нақты сандары бар деп ұйғарайық. Теңсіздіктердің транзитивтік қасиеті бойынша
болатындай х
1
және х
2
нақты сандары бар деп ұйғарайық. Теңсіздіктердің транзитивтік қасиеті бойынша
 . 6-тұжырым негізінде х
1
= х
2
дәлелдемегіміз де осы еді.
. 6-тұжырым негізінде х
1
= х
2
дәлелдемегіміз де осы еді.
Анықтама.
Егер
a
>0, (
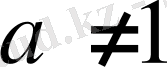 ) және
b
>0 болса, онда нақты
α
саны
b
санының
a
негізі бойынша логарифмі деп аталады да, егер
) және
b
>0 болса, онда нақты
α
саны
b
санының
a
негізі бойынша логарифмі деп аталады да, егер
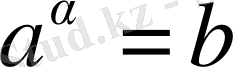 болса,
болса,
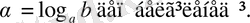
Логарифмнің анықтамасын 1-теореманы дәлелдегеннен кейін беруге болатынын ескертейік, өйткені
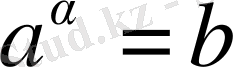 болатындай
α
саны бар ма, ол жалғыз ба, оған дейін айқын емес еді. Логарифм тек 1-ге тең емес оң негіз бойынша оң сан үшін анықталатынын тағы да атап өтейік, яғни кез келген
а
≤0,
а
=1 және
b
≤0 үшін логарифм ұғымының мағынасы жоқ. Мысалы, (-8) санының (-2) негізі бойынша логарифмі 3 саны деген тұжырымның мағынасы болмайды.
болатындай
α
саны бар ма, ол жалғыз ба, оған дейін айқын емес еді. Логарифм тек 1-ге тең емес оң негіз бойынша оң сан үшін анықталатынын тағы да атап өтейік, яғни кез келген
а
≤0,
а
=1 және
b
≤0 үшін логарифм ұғымының мағынасы жоқ. Мысалы, (-8) санының (-2) негізі бойынша логарифмі 3 саны деген тұжырымның мағынасы болмайды.
Сөйтіп,
log
a
b
логарифмінің анықтамасында әрқашан
a
>0, (
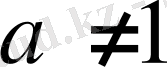 ) ,
b
>0. Логарифмнің анықтамасынан негізгі тепе-теңдік
) ,
b
>0. Логарифмнің анықтамасынан негізгі тепе-теңдік
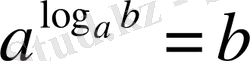
шығады. Логарифм анықтамасымен пайдаланып,
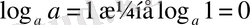 екенін аламыз. Логарифмнің жалғыз ғана болатынын пайдалансақ, егер
екенін аламыз. Логарифмнің жалғыз ғана болатынын пайдалансақ, егер
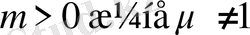 болса, онда әрқашан
болса, онда әрқашан
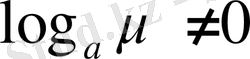 .
.
Логарифмдердің негізгі қасиеттерін қарастыруға көшейік.
M, N, a, b, α және β сандары үшін M>0, N>0, a>0, b>0, a≠1 b≠1. α мен β кез келген нақты сандар (b≠0) болсын. Онда:
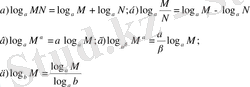
(бірнегізді логарифмнен екінші негізді логарифмге көшу ережесі) ;
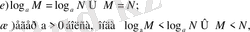
З) егер 0<0<1 болса, онда
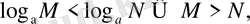
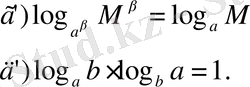
Осы қасиеттерді дәлелдейік.
а)
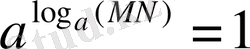 өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
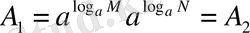 оң санның дәрежесінің қасиеті бойынша
оң санның дәрежесінің қасиеті бойынша
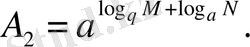 Сонымен
Сонымен
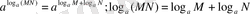 теңдігін аламыз. б) қасиеті де осы сияқты дәлелденеді.
теңдігін аламыз. б) қасиеті де осы сияқты дәлелденеді.
в)
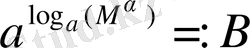 өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
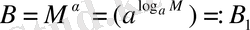 , оң санның дәрежесінің қасиеті бойынша
, оң санның дәрежесінің қасиеті бойынша
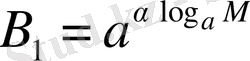 . Сөйтіп,
. Сөйтіп,
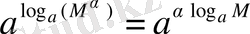 . Дәрежелердің қасиеттерінің 6-тұжырымын қолданып,
. Дәрежелердің қасиеттерінің 6-тұжырымын қолданып,
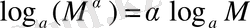 екенін аламыз.
екенін аламыз.
г)
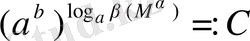 өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
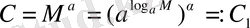 , оң санның дәрежесінің қасиеті бойынша
, оң санның дәрежесінің қасиеті бойынша
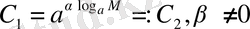 болғандықтан
болғандықтан
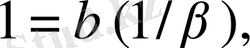 сондықтан
сондықтан
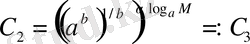 , оң санның дәрежесінің қасиеті бойынша
, оң санның дәрежесінің қасиеті бойынша
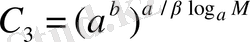 . Сөйтіп,
. Сөйтіп,
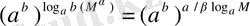 . Соңғы теңдікке дәрежелер қасиеттерінің 6-тұжырымын қолданып,
. Соңғы теңдікке дәрежелер қасиеттерінің 6-тұжырымын қолданып,
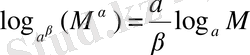 теңдігін аламыз.
теңдігін аламыз.
д)
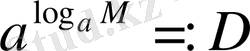 өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
өрнегін қарастырайық: негізгі логарифмдік тепе-теңдік бойынша
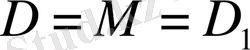 негізгі логарифмдік тепе-теңдік бойынша
негізгі логарифмдік тепе-теңдік бойынша
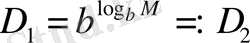 негізгі логарифмдік тепе-теңдік бойынша
негізгі логарифмдік тепе-теңдік бойынша
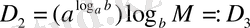 оң санның дәрежесінің қасиеті бойынша
оң санның дәрежесінің қасиеті бойынша
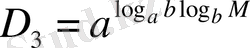 . Сөйтіп,
. Сөйтіп,
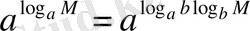 . Соңғы теңдікке дәрежелер қасиеттерінің 6-тұжырымын қолданып,
. Соңғы теңдікке дәрежелер қасиеттерінің 6-тұжырымын қолданып,
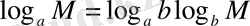 екенін аламыз. Теңдіктердің қасиеті бойынша осы теңдіктің екі жағын
екенін аламыз. Теңдіктердің қасиеті бойынша осы теңдіктің екі жағын
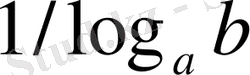 санына (өйткені
санына (өйткені
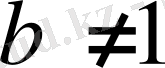 болса, онда
болса, онда
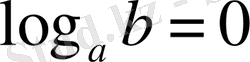 ) көбейтеміз, сонда
) көбейтеміз, сонда
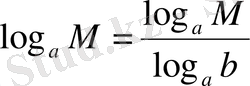
теңдігінің дұрыстығы шығады.
е)
Негізгі логарифмдік тепе-теңдік бойынша
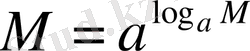 және
және
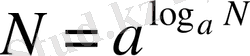 , демек,
, демек,
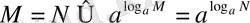 (1)
(1)
Дәрежелер қасиеттерінің 6-тұжырымы бойынша
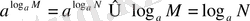 (2)
(2)
(1) мен (2) -ден
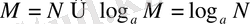 екені шығады.
екені шығады.
ж)
Негізгі логарифмдік тепе-теңдік бойынша
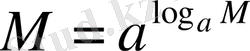 және
және
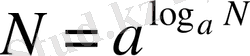 , демек,
, демек,
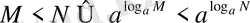 (3)
(3)
Дәрежелер қасиеттерінің 4-тұжырымы негізінде алатынымыз:
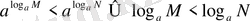 (4)
(4)
(3) пен (4) -тен
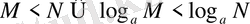 екені шығады. (3) қасиеті де осы сияқты дәлелденеді.
екені шығады. (3) қасиеті де осы сияқты дәлелденеді.
ж) мен з) қасиеттерін сөзбен былайша айта аламыз:
негізі бірден үлкен болғанда екі оң санның кішісіне үлкен логарифм және үлкен логарифмге кіші сан сәйкес келеді.
Негізі 10 болатын логарифмдер ондық логарифмдер деп аталады да
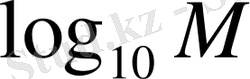 белгілеуінің орнына көбінесе
белгілеуінің орнына көбінесе
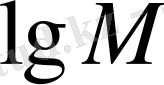 белгілеуі қолданылады. Негізі
е
(
е
- иррационал сан, оның жуық мәні 2, 71828 . . . ) болатын логарифмдер натурал логарифмдер деп аталады да
белгілеуі қолданылады. Негізі
е
(
е
- иррационал сан, оның жуық мәні 2, 71828 . . . ) болатын логарифмдер натурал логарифмдер деп аталады да
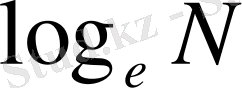 белгілеуі орнына көбінесе
белгілеуі орнына көбінесе
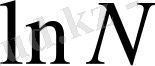 белгілеуі қолданылады.
белгілеуі қолданылады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz