Дифференциалдық теңдеулер: бірінші ретті әдістер және екінші ретті тұрақты коэффициентті сызықтық теңдеулер


VII тарау
Дифференциалдық теңдеулер.
- 27 Дифференциалдық теңдеу ұғымы.
1. Дифференциалдық теңдеуге келтірілетін есептер
Анықтама. Құрамында тәуелсіз айнымалы х, ізделінді
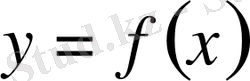 функциясы және оның туындылары болатын теңдеу дифференциалдық теңдеу деп аталады.
функциясы және оның туындылары болатын теңдеу дифференциалдық теңдеу деп аталады.
Есеп. ХОУ жазықтығында О (0; 0) нүктесі арқылы өтіп, кез келген нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті сол нүктенің екі еселенген абциссасына тең болатын қисықтың теңдеуін табу керек.
Шешуі: Ізделінді функция
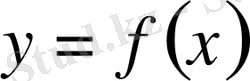 болсын. Есептің шарты бойынша
болсын. Есептің шарты бойынша
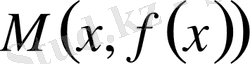 нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті
k
=2х болады. Ал, туындының геометриялық мағынасынан
нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті
k
=2х болады. Ал, туындының геометриялық мағынасынан
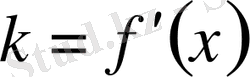 екені белгілі. Сонда
екені белгілі. Сонда
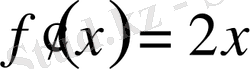 немесе
немесе
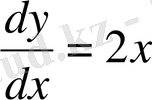 (1)
(1)
болады.
Бұл (1) теңдеу дифференциалдық теңдеу, өйткені оның құрамында ізделінді функцияның туындысы бар. Оны
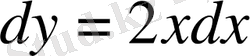 түрінде жазамыз. Бұдан ізделінді функция 2х-тің алғашқы функциясы болады.
түрінде жазамыз. Бұдан ізделінді функция 2х-тің алғашқы функциясы болады.
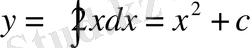 ,
,
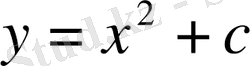 (2)
(2)
(2) теңдеуден (1) дифференциалдық теңдеудің шексіз көп шешімі бар екенін көреміз, яғни (1) теңдеуді шексіз көп қисық - парабола қанағаттандырады (1-сызба) .
Осы қисықтардың ішінен өзімізге қажеттісін таңдап алу үшін есептің шартындағы ізделінді қисық
О
(0; 0) нүктесі арқылы өтеді деген шартты пайдаланамыз. Осы нүктенің координаталары (2) теңдеуді қанағаттандыруы тиіс. Сонда 0 = 0 +
c
, яғни
с
= 0 болады. Сонымен, ізделінді қисықтың теңдеуі
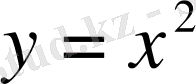 Equation. 3 .
Equation. 3 .
Егер ізділінді функция бір айнымалының функциясы болса, онда оны қарапайым дифференциалдық теңдеу деп атайды.
Оның жалпы түрі
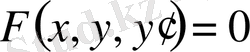 (3)
(3)
болады.
Дифференциалдық теңдеуге енетін функцияның туындысының ең жоғарғы реті дифференциалдық теңдеудің реті деп аталады.
n-ші ретті дифференциалдық теңдеудің жалпы түрі мынандай:
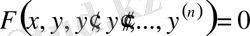 (4)
(4)
Дербес жағдайда теңдеудің құрамына х, у және n-нен төменгі туындылар кірмеуі мүмкін. Мысалы,
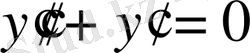 Equation. 3 .
Equation. 3 .
(4) теңдікті қанағаттандыратын
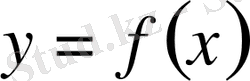 функциясы дифференциалдық теңдеудің
шешімі
деп аталады.
функциясы дифференциалдық теңдеудің
шешімі
деп аталады.
Мысалдар.
- функциясытеңдеуінің шешімі болатынын көрсету керек.
Шешуі:
 -ті табайық:
-ті табайық:
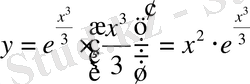 .
.
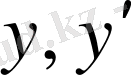 мәндерін берілген теңдеуге қоямыз. Сонда
мәндерін берілген теңдеуге қоямыз. Сонда
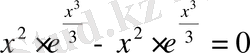 , бұдан
, бұдан
 шықты. Демек,
шықты. Демек,
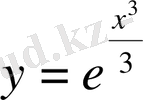 функциясы берілген дифференциалдық теңдеуді қанағаттандырды, яғни оның шешімі болады.
функциясы берілген дифференциалдық теңдеуді қанағаттандырды, яғни оның шешімі болады.
- теңдеуінің шешімі болатынын көрсету керек.
Шешуі:
2. Бірінші ретті дифференциалдық теңдеу, оның жалпы шешімі және алғашқы шарттары.
Бірінші ретті дифференциалдық теңдеудің жалпы түрі
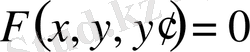 немесе
немесе
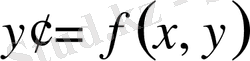 (5)
(5)
болады.
Дифференциалдық теңдеуді шешкенде оның шешіміне
С
тұрақтысы енеді. Мұндай шешімдер дифференциалдық теңдеудің
жалпы шешімі
деп аталады. Ол
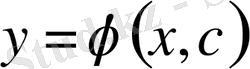 түрінде болады.
түрінде болады.
Берілген дифференциалдық теңдеуді шешу немесе интегралдау - оның жалпы шешімін табу болады. Дифференциалдық теңдеудің жалпы шешімінен С - тұрақтысының белгілі бір мәніндегі шешімін дифференциалдық теңдеудің дербес шешімі деп аталады.
 болғандықтан у функциясы у
0
мәнін қабылдаса, бұл шартты дифференциалдық теңдеудің
алғашқы шарты
деп аталады. Алғашқы шарт арқылы дифференциалдық теңдеудің жалпы шешімінен дербес шешімін табуға болады. Шынында да,
болғандықтан у функциясы у
0
мәнін қабылдаса, бұл шартты дифференциалдық теңдеудің
алғашқы шарты
деп аталады. Алғашқы шарт арқылы дифференциалдық теңдеудің жалпы шешімінен дербес шешімін табуға болады. Шынында да,
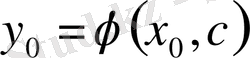 теңдеуінен
С
-ның белгілі бір
С
=
С
0
мәнін тауып, жалпы шешімге қойсақ, дербес шешім
теңдеуінен
С
-ның белгілі бір
С
=
С
0
мәнін тауып, жалпы шешімге қойсақ, дербес шешім
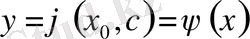 болады.
болады.
3. Айнымалыларын бөлектеуге болатын дифференциалдық теңдеу.
Бірінші ретті дифференциалдық теңдеуді мына түрде жазайық:
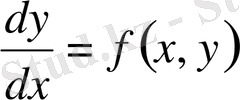 немесе
немесе
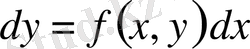 .
.
Бұл теңдеуді жалпы түрде мынандай формада қарастыруға болады:
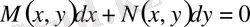 (6)
(6)
Мұндағы х , у айнымалыларының біреуін екіншісінің функциясы деп есептеуге болады.
 және
және
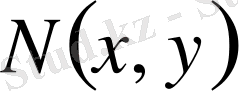 функциялары мынандай функциялардың көбейтіндісі болсын:
функциялары мынандай функциялардың көбейтіндісі болсын:
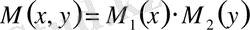
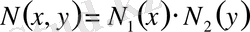 .
.
Бұл көбейткіштердің әрқайсысы бір ғана айнымалыға тәуелді. Сонда (6) теңдеу
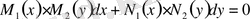 (7)
(7)
түрінде жазылады. (7) теңдіктің екі жағын да
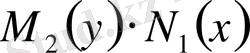 көбейтіндісіне мүшелеп бөлеміз (бұл көбейтіндіні нольге тең емес деп ұйғарамыз) . Сонда
көбейтіндісіне мүшелеп бөлеміз (бұл көбейтіндіні нольге тең емес деп ұйғарамыз) . Сонда
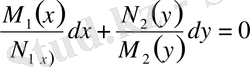 (8)
(8)
(8) теңдеудегі dx -тің алдындағы көбейткіш тек қана x айнымалысының, ал dy -тің алдындағы көбейткіш тек қана у айнымалысының функциясы. Сондықтан (8) теңдеу айнымалылары бөлектенген , ал (7) теңдеу айнымалылары бөлектенетін дифференциалдық теңдеу деп аталады.
Бұл теңдеудің жалпы шешімі мына түрде табылады:
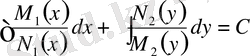 (9)
(9)
Мысалдар.
- теңдеуінің жалпы шешімін табу керек.
Шешуі: Берілген теңдеу айнымалылары бөлектенетін теңдеу.
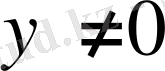 деп ұйғарып, теңдіктің екі жағын да у-ке бөліп,
dx
-ке көбейтейік. Сонда
деп ұйғарып, теңдіктің екі жағын да у-ке бөліп,
dx
-ке көбейтейік. Сонда
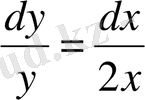 - айнымалылары бөлектенген теңдеу алынады. (9) формула бойынша теңдеудің екі жағын да интегралдасақ,
- айнымалылары бөлектенген теңдеу алынады. (9) формула бойынша теңдеудің екі жағын да интегралдасақ,
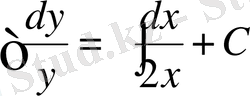 . Бұдан
. Бұдан
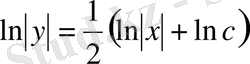 ,
,
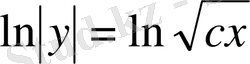 , яғни
, яғни
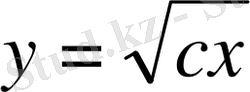 .
.
- теңдеуін интегралдау керек.
Шешуі: Дифференциалдық теңдеуді интегралдау - оның шешімін табу деген сөз.
Теңдеудің екі жағын да
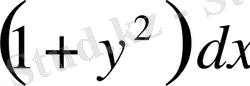 -ке көбейтіп, айнымалылары бөлектенген теңдеу аламыз:
-ке көбейтіп, айнымалылары бөлектенген теңдеу аламыз:
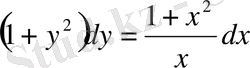 немесе
немесе
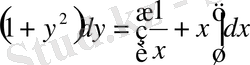 .
.
Осы теңдеуді интегралдау арқылы берілген теңдеудің жалпы шешімін табамыз:
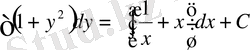 ,
,
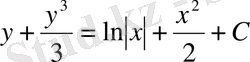 .
.
Бұдан
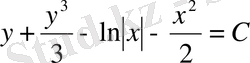 .
.
- теңдеуін шешу керек.
Шешуі: Бұл айнымалылары бөлектенетін теңдеу. Теңдеуді
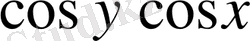 -қа бөліп (
-қа бөліп (
 деп есептейміз), мына теңдеуді аламыз;
деп есептейміз), мына теңдеуді аламыз;
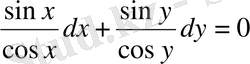
Бұдан
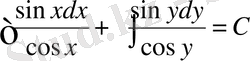 ;
;
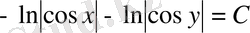 немесе
немесе
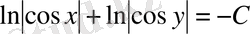 .
.
Бұл теңдеуді потенцирлеп, берілген дифференциалдық теңдеудің жалпы шешімін аламыз.
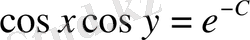 , мұндағы
, мұндағы
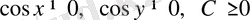 .
.
4. Бірінші ретті біртектес дифференциалдық теңдеу.
Анықтама
. Егер
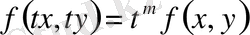 теңдігі орындалса, онда
теңдігі орындалса, онда
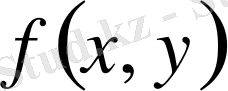 функциясы
m
өлшемді біртектес функция
деп атайды.
функциясы
m
өлшемді біртектес функция
деп атайды.
Мысал.
- функциясы үш өлшемді біртектес функция. Себебі, хжәнеуаргументтерінt-ға көбейтсек,
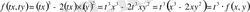
- - ноль өлшемді біртектес функция екенін көрсетейік.
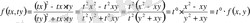
Егер
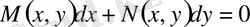 (1)
(1)
теңдеуіндегі
 және
және
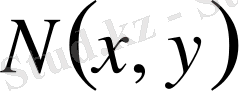 функциялары бірдей өлшемді біртектес функция болса, олда бұл теңдеу сол
өлшемді біртектес дифференциалдық теңдеу
деп аталады.
функциялары бірдей өлшемді біртектес функция болса, олда бұл теңдеу сол
өлшемді біртектес дифференциалдық теңдеу
деп аталады.
(1) теңдеуге
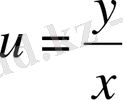 ауыстыруын қолданып, оны айнымалылары бөлектенетін теңдеуге оңай келтіруге болатынын көрсетуге болады. Мұндағы u функциясы
х
-ке тәуелді ізделінді функция. Сонда бұл ауыстырудан
ауыстыруын қолданып, оны айнымалылары бөлектенетін теңдеуге оңай келтіруге болатынын көрсетуге болады. Мұндағы u функциясы
х
-ке тәуелді ізделінді функция. Сонда бұл ауыстырудан
 , ал
, ал
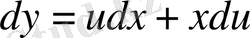 болады.
болады.
Кейбір есептерде
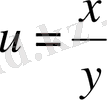 аустыруын жасау қолайлы болады.
аустыруын жасау қолайлы болады.
Мысалдар.
- теңдеуін шешу керек.
Шешуі
.
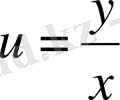 ауыстыруын жасайық.
ауыстыруын жасайық.
Сонда
 ,
,
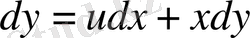 . Бұдан берілген теңдеу
. Бұдан берілген теңдеу
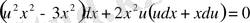
түріне келеді. Ұқсас мүшелерін біріктірсек,
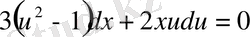
болады. Бұл айнымалылары бөлектенетін теңдеу. Теңдеудің екі жағын да
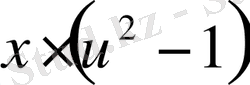 -ге бөлсек,
-ге бөлсек,
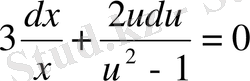 теңдеуін аламыз. Бұдан
теңдеуін аламыз. Бұдан
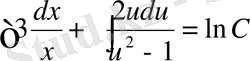 ,
,
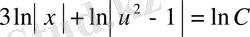 .
.
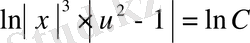 потенцирлесек,
потенцирлесек,
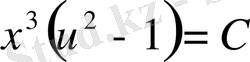 болады. Енді
болады. Енді
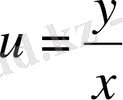 ауыстыруын
u
-дың орына қойсақ,
ауыстыруын
u
-дың орына қойсақ,
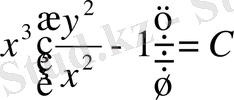 немесе
немесе
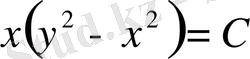 болады.
болады.
2.
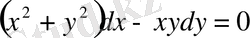 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі:
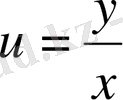 болсын, бұдан
болсын, бұдан
 ,
,
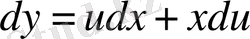 . Бұл өрнектерді берілген теңдеуге қойсақ,
. Бұл өрнектерді берілген теңдеуге қойсақ,
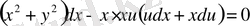 ;
;
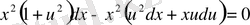 .
.
 деп ұйғарып, теңдеуді
деп ұйғарып, теңдеуді
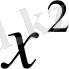 -ке бөлсек,
-ке бөлсек,
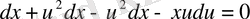 ,
,

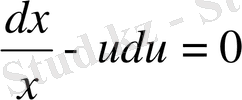 ,
,
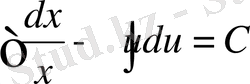
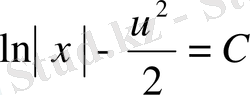 немесе
немесе
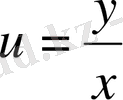 болғандықтан,
болғандықтан,
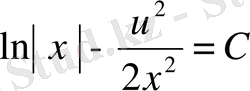 .
.
Бұл берілген теңдеудің жалпы шешімі. Оны мына түрде де жазуға болады:
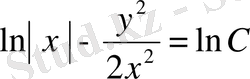 ;
;
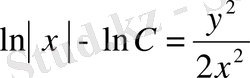 ;
;
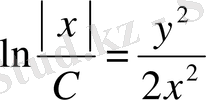 , бұдан
, бұдан
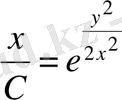 ,
,
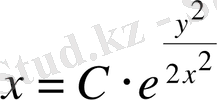 .
.
5. Бірінші ретті сызықтық дифференциалдық теңдеу.
Анықтама . Егер теңдеу ізделінді функция мен оның туындысына қатысты бірінші дәрежелі болса, онда оны бірінші ретті сызықтық дифференциалдық теңдеу деп атайды.
Анықтама бойынша бірінші ретті сызықтық дифференциалдық теңдеу мына түрде болады:
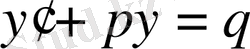 (1)
(1)
мұндағы
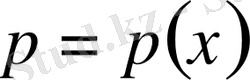 ,
,
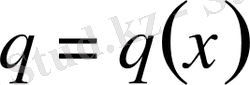 .
.
(1) теңдеуді шешу үшін
 ауыстыруын қолданамыз, мұндағы
ауыстыруын қолданамыз, мұндағы
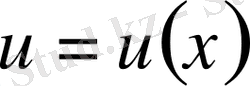 ,
,
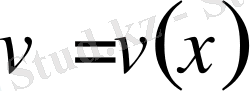 . Сонда,
. Сонда,
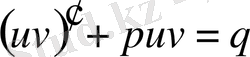 болады.
болады.
Бұдан
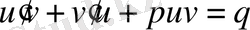 ;
;
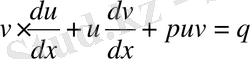 ;
;
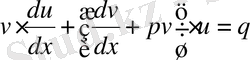 (2)
(2)
Еркімізше алынған
v
функциясы
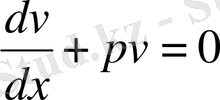 шартын қанағаттандырсын. Осы теңдеудің айнымалыларын бөлектеп шешсек,
шартын қанағаттандырсын. Осы теңдеудің айнымалыларын бөлектеп шешсек,
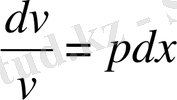 ,
,
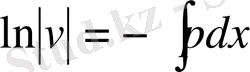 , бұдан
, бұдан
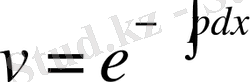 (3)
(3)
Сонда (2) теңдеуге (3) өрнекті қойсақ,
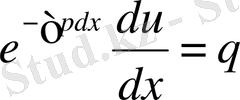 ;
;
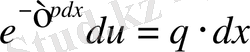 ;
;
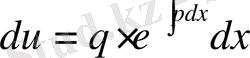 ;
;
бұдан
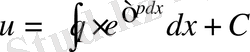 (4)
(4)
 болғандықтан (3) және (4) теңдіктердің пайдалансақ,
болғандықтан (3) және (4) теңдіктердің пайдалансақ,
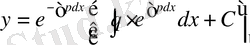 (5)
(5)
түрдегі жалпы шешімін аламыз.
Егер (1) теңдеудегі
 болса, онда оны
бірінші ретті біртектес сызықтық
дифференциалдық теңдеу деп атайды.
болса, онда оны
бірінші ретті біртектес сызықтық
дифференциалдық теңдеу деп атайды.
Мысалдар.
- теңдеуін шешу керек.
Шешуі: Мұндағы
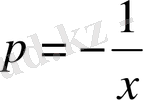 ,
,
 . Сонда (5) формуланы қолдансақ,
. Сонда (5) формуланы қолдансақ,
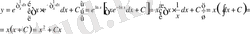
- теңдеуін шешу керек.
Шешуі:
 ,
,
 .
.
 ауыстыуын жасап,
ауыстыуын жасап,
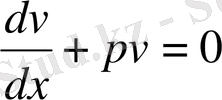 теңдеуін шешсек,
теңдеуін шешсек,
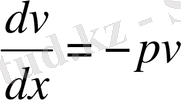 , яғни
, яғни
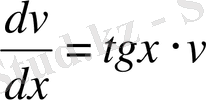
бұдан
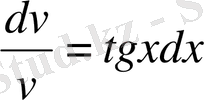 ,
,
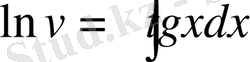 ,
,
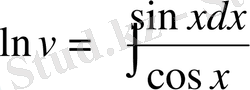 ,
,
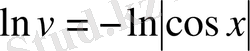 , бұдан
, бұдан
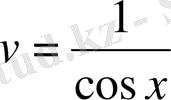 болады.
болады.
Сонда берілген теңдеу
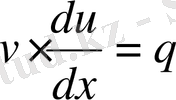 , яғни
, яғни
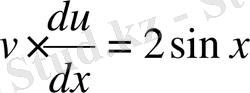 болады. Бұдан
болады. Бұдан
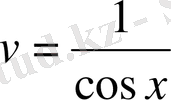 екенін ескерсек,
екенін ескерсек,
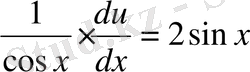 ,
,
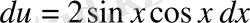 немесе
немесе
 ;
;
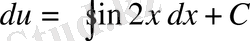 ;
;
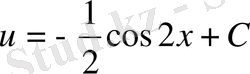 .
.
 болғандықтан, ізделінді функция
болғандықтан, ізделінді функция
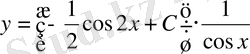 немесе
немесе
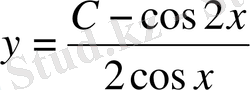 .
.
- теңдеуін шешу керек.
Шешуі:
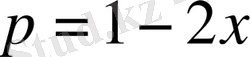 ,
,
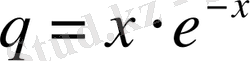 .
.
 ауыстыруын қолданып,
ауыстыруын қолданып,
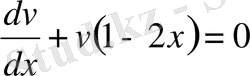 және
және
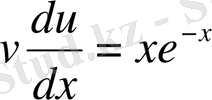 теңдеулерінен
u
,
v
мәндерін табамыз.
теңдеулерінен
u
,
v
мәндерін табамыз.
Бірінші теңдеуді шешейік.
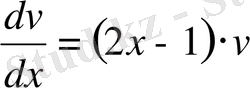 ,
,
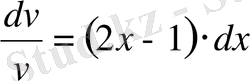
бұдан
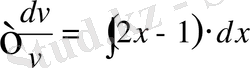 ,
,
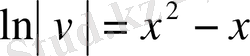 ,
,
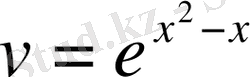 .
.
v -ның табылған мәнін екінші теңдеуге қойсақ,
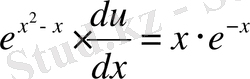 .
.
Бұдан
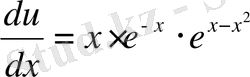 ;
;
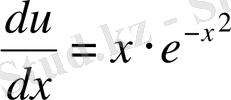 ;
;
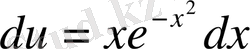 ;
;
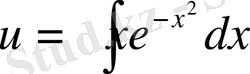 ;
;
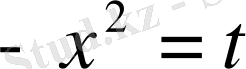 ауыстыруын жасасақ,
ауыстыруын жасасақ,
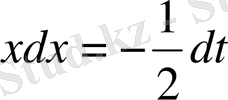 .
.
Сонда
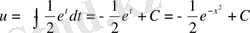 . Сонымен
. Сонымен
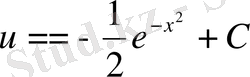 .
.
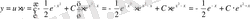 , яғни теңдеудің жалпы шешімі
, яғни теңдеудің жалпы шешімі
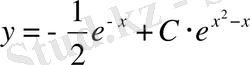 болды.
болды.
- 28 Екінші ретті дифференциалдық теңдеулер.
1. Бірінші ретті теңдеуге келтірілетін екінші ретті дифференциалдық теңдеулер.
1°
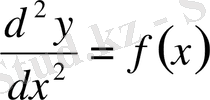 түріндегі екінші ретті дифференциалдық теңдеуді шешу үшін оның ретін төмендетіп, былайша шешеміз:
түріндегі екінші ретті дифференциалдық теңдеуді шешу үшін оның ретін төмендетіп, былайша шешеміз:
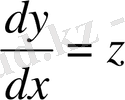 болсын, сонда
болсын, сонда
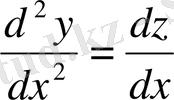 болады да
болады да
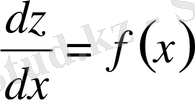 түріндегі бірінші ретті дифференциалдық теңдеу аламыз. Бұдан
түріндегі бірінші ретті дифференциалдық теңдеу аламыз. Бұдан
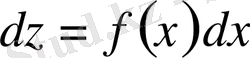 . Бұл теңдеудің екі жағын да интегралдасақ,
. Бұл теңдеудің екі жағын да интегралдасақ,
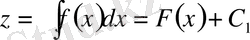 болады.
болады.
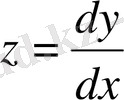 деген белгілеуге көшсек,
деген белгілеуге көшсек,
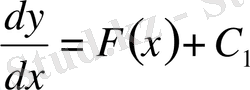 түріндегі бірінші ретті дифференциалдық теңдеу аламыз. Бұдан
түріндегі бірінші ретті дифференциалдық теңдеу аламыз. Бұдан
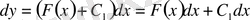 .
.
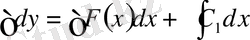 ;
;
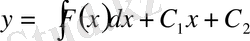 берілген теңдеудің жалпы шешімі болады.
берілген теңдеудің жалпы шешімі болады.
Мысал.
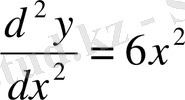 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі.
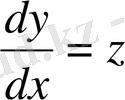 деп белгілейік, сонда
деп белгілейік, сонда
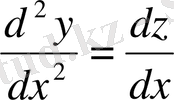 болады да,
болады да,
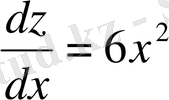 , бұдан
, бұдан
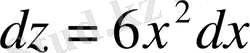 ;
;
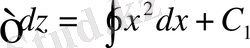 ;
;
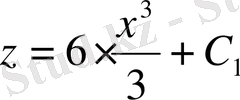 ;
;
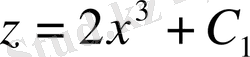 , немесе
, немесе
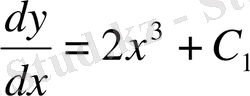 .
.
Осы теңдеуді интегралдасақ,
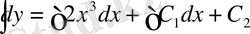
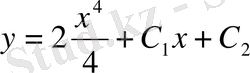 ;
;
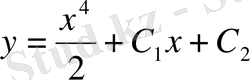 болады.
болады.
2°
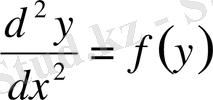 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі.
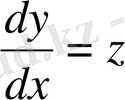 түріндегі белгілеуін енгіземіз. Сонда
түріндегі белгілеуін енгіземіз. Сонда
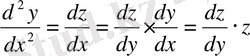 болады
болады
Сонымен
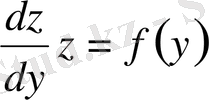 түріндегі айнымалылары бөлектенетін дифференциалдық теңдеу алдық. Бұдан,
түріндегі айнымалылары бөлектенетін дифференциалдық теңдеу алдық. Бұдан,
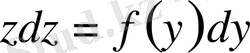 .
.
Осы теңдеуді интегралдап z-ті тапқаннан кейін, оны
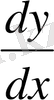 -пен ауыстырып,
х
пен
у
-ке қатысты айнымалыны бөлектеуге болатын теңдеу аламыз.
-пен ауыстырып,
х
пен
у
-ке қатысты айнымалыны бөлектеуге болатын теңдеу аламыз.
2. Тұрақты коэффициентті сызықтық біртектес екінші ретті дифференциалдық теңдеулер.
1° Анықтама бойынша екінші ретті сызықтық дифференциалдық теңдеудің жалпы түрі мынандай болады:
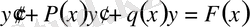 (1)
(1)
Егер
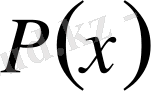 және
және
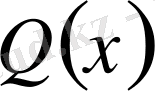 - тұрақты, ал
- тұрақты, ал
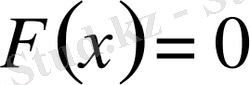 болса, онда екінші ретті сызықтық теңдеу
тұрақты коэффициентті бертектес теңдеу
деп аталады.
болса, онда екінші ретті сызықтық теңдеу
тұрақты коэффициентті бертектес теңдеу
деп аталады.
Сонымен тұрақты коэффициентті сызықтық біртектес екінші ретті дифференциалдық теңдеу
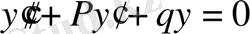 (2)
(2)
түрінде болады.
2° у 1 және у 2 функциялары (2) теңдеудің шешімдері болсын.
Анықтама
. Егер
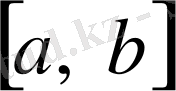 кесіндісінен алынған кез келген х үшін
кесіндісінен алынған кез келген х үшін
 теңдігі орындалатындай
теңдігі орындалатындай
 саны табылса, онда
у
1
және
у
2
шешімдері
саны табылса, онда
у
1
және
у
2
шешімдері
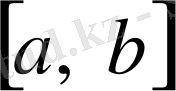 кесіндісінде сызықты тәуелді деп, ал егер осындай
кесіндісінде сызықты тәуелді деп, ал егер осындай
 саны табылмаса, онда
у
1
және
у
2
шешімдері сызықты тәуелсіз деп аталады, яғни
саны табылмаса, онда
у
1
және
у
2
шешімдері сызықты тәуелсіз деп аталады, яғни
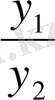 қатынасы
қатынасы
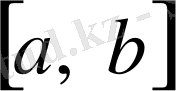 кесіндісінде тұрақты болмайды.
кесіндісінде тұрақты болмайды.
Теорема 1 . (2) теңдеудің у 1 шешімін С тұрақты санына көбейтсек, ол да осы теңдеудің шешімі болады.
Дәлелдеу
.
 -ді (2) теңдеуге қояйық.
-ді (2) теңдеуге қояйық.
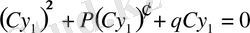 , бұдан
, бұдан
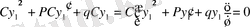 ,
,
себебі
у
1
берілген теңдеудің шешімі болғандықтан
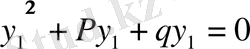 болады. Бұдан
болады. Бұдан
 -дің (2) теңдеудің шешімі болатындығын көрдік.
-дің (2) теңдеудің шешімі болатындығын көрдік.
Теорема 2. (2) теңдеудің у 1 және у 2 шешімдерінің қосындысы да (2) теңдеудің шешімі болады.
Дәлелдеу
.
 қосындысын (2) теңдеуге қояйық:
қосындысын (2) теңдеуге қояйық:
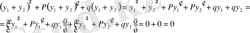
Демек
 берілген (2) теңдеудің шешімі болды.
берілген (2) теңдеудің шешімі болды.
Теорема 3 . Егер у 1 және у 2 функциялары (2) теңдеудің сызықтық тәуелсіз шешімдері, ал С 1 мен С 2 - кез келген тұрақты сандар болса, онда
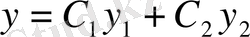
функциясы да (2) теңдеудің шешімі болады.
Бұл теоремадан сызықтық біртектес екінші ретті дифференциалдық теңдеудің жалпы шешімін оның кез келген екі сызықтық тәуелсіз дербес шешімі арқылы табуға болатынын көреміз.
 ауыстыруын жасау арқылы теңдеудің екі дербес шешімін табуға болады. Бұл жағдайда (2) теңдеу мына түрде болады:
ауыстыруын жасау арқылы теңдеудің екі дербес шешімін табуға болады. Бұл жағдайда (2) теңдеу мына түрде болады:
 ,
,
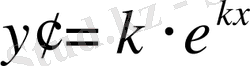 ,
,
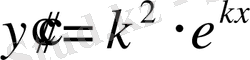 болғандықтан
болғандықтан
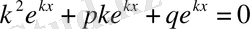 немесе
немесе
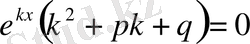 .
.
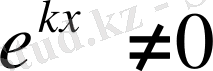 болғандықтан
болғандықтан
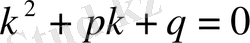 (3)
(3)
болады.
(3) теңдеу сызықтық біртектес теңдеудің характеристикалық (сипаттамалық) теңдеуі деп аталады.
Мынандай жағдайлар болуы мүмкін:
- (3) теңдеудің нақты сандар:Equation. 3 . Сонда, функциялары (2) теңдеудің сызықтық тәуелсіз шешімдері болады да, оның жалпы шешімі
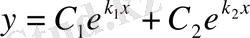 (4)
(4)
түрде болады.
- (3) теңдеудің түбірлері өз ара тең нақты сандар:. Бұл жағдайда бір дербес шешімдіал екіншісінтүрінде аламыз. у1жәнеу2шешімдері сызықты тәуелсіз, себебі. Сондықтан 3-теорема бойынша (2) теңдеудің жалпы шешімі
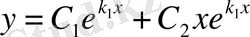 немесе
немесе
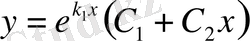 (5)
(5)
түрінде болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz