Евклид кеңістігінің теориясы: скаляр көбейтінді, норма, ортонормалданған базис және изоморфизм


Евклид кеңістігінің қасиеттері
Анықтама.
Нақты сызықты векторлық
R
кеңістіктің кез келген екі х, у
 R элементіне (векторына)
скаляр көбейтінді
деп аталатын
(х, у)
нақты саны сәйкес келсе және оған мына төмендегі аксиомалар орындалса:
R элементіне (векторына)
скаляр көбейтінді
деп аталатын
(х, у)
нақты саны сәйкес келсе және оған мына төмендегі аксиомалар орындалса:
1. (х, у) = (у, х),
2. (
х, у) =
(х, у),
- нақты сан,
3. (х + у, z) = (х, z) + (у, z ),
4. (х, х) > 0, егер х
0, (х, х) = 0, егер х = 0,
онда бұл кеңістікті нақты Евклид кеңістігі деп атайды.
Евклид кеңістігі кез келген шекті өлшемді немесе шексіз өлшемді болып бөлінеді.
Скаляр кебейтіндінің 1) - 3) аксиомаларын пайдаланып, оның мына төмендегі қасиеттерін дәлелдейік:
1. (х,
у) =
(х, у) .
2. (х, у + z) = (х, у) + (х, z) .
3. (

х
+
. . . +
) =
+ . . . +
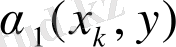
4.
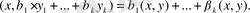
Шынында да,
1.
(х,
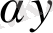 ) = (
) = (
 у, х) =
у, х) =
 (у, х) =
(у, х) =
 (х, у) .
(х, у) .
2. (х, у + z) = (у + z, х) = (у, х) + (z, х) = (х, у) + (х, z) .
3. (
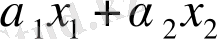 + . . . +
а
к
х
к
, у) =
+ . . . +
а
к
х
к
, у) =

4.
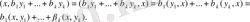
Мысалдар.
1.
[а, b]
сегментінде анықталған және үзіліссіз
х (t)
функциялар
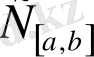 жиынын қарастыралық, яғни
х(t)
жиынын қарастыралық, яғни
х(t)
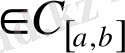 . Енді
х (t), у(t)
функциялары
. Енді
х (t), у(t)
функциялары
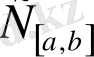 жиынының элементтері болсын:
х(t), у(t)
жиынының элементтері болсын:
х(t), у(t)
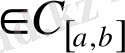 және олардың скаляр көбейтіндісі:
және олардың скаляр көбейтіндісі:
(х(t), у(t) ) =
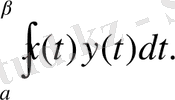
формуламен өрнектелсін.
анықталған скаляр көбейтіндіге жоғарыдағы төрт аксиома орындалады. Олай болса үзіліссіз функциялар
[а, b
] жиыны евклид кеңістік:
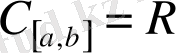 және ол шексіз өлшемді.
және ол шексіз өлшемді.
2. Нақты
п
сандар
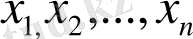 жиынын
жиынын
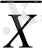 вектордың координаттары деп қарастыралық: x =
вектордың координаттары деп қарастыралық: x =

x =
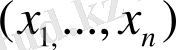 пен у=(у
пен у=(у
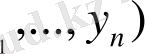 векторларды қосу, оларды
векторларды қосу, оларды
 нақты санға көбейту (х + у) =
нақты санға көбейту (х + у) =

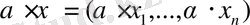
формуларымен анықтайық, ал олардың скаляр көбейтіндісін
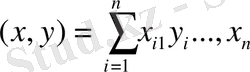 (2)
(2)
формуламен өрнектейік, (2) формуламен өрнектелген скаляр көбейтіндіге анықтамадағы төрт аксиома түгелімен орындалады. Олай болса, бұл векторлар жиыны n -өлшемді евклид кеңістік.
б) Евклид кеңістігінің нормасы және оның қасиеттері
Евклид R кеңістігінің анықтамасындағы 4-аксиома бойынша кез келген
х
 0 элементтің (вектордың) скаляр
(х, х)
көбейтіндісі нақты оң сан. Сондықтан, бұл скаляр
(х, х)
көбейтіндіден квадрат түбір былай табылады:
0 элементтің (вектордың) скаляр
(х, х)
көбейтіндісі нақты оң сан. Сондықтан, бұл скаляр
(х, х)
көбейтіндіден квадрат түбір былай табылады:
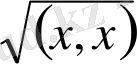
Анықтама.
Евклид
R
кеңістігінің
х
 0 элементіне сәйкес
келетін
(х, х)
скаляр көбейтіндінің квадрат түбірін
0 элементіне сәйкес
келетін
(х, х)
скаляр көбейтіндінің квадрат түбірін
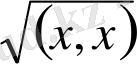 оның нормасы (немесе ұзындығы, модулі) деп атаймыз және оны
оның нормасы (немесе ұзындығы, модулі) деп атаймыз және оны
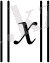 символымен белгілеп, мына төмендегі
символымен белгілеп, мына төмендегі
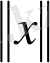 =
=
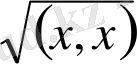 формуламен өрнектейміз.
формуламен өрнектейміз.
Теорема.
Евклид
R
кеңістігінің кез келген
х, у
 элементіне Коши
элементіне Коши
(х,
у)
2
 (
х, х
)
(у, у)
(3)
(
х, х
)
(у, у)
(3)
немесе
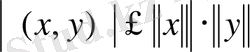
теңсіздігі орындалады.
Дәлелдеуі.
Егер
 нақты сан болса, онда
нақты сан болса, онда
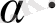 х-у
векторы үшін
х-у
векторы үшін
(
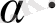 х - у,
х - у,
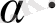 х - у)
х - у)
 0
0
теңсіздігі орындалады.
Бұдан
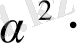 (х, х) -2
(х, х) -2
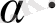 (х, у) + (у, у)
(х, у) + (у, у)
 0.
0.
 -байланысты бұл квадратты үшмүшеліктің теріс болмауы үшін оның дискриминанты оң болмауы:
-байланысты бұл квадратты үшмүшеліктің теріс болмауы үшін оның дискриминанты оң болмауы:
(х,
у)
2
- (х, х) (у, у)
 0.
0.
қажетті әрі жеткілікті. Осы теңсіздіктен (4. 3) теңсіздігі алынады. Теорема дәлелденді.
Теорема.
Евклид
R
кеңістігінің кез келген екі
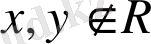 элементіне (векторына) :
элементіне (векторына) :
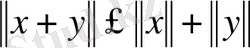 (4)
(4)
үшбұрыш теңсіздігі орындалады.
Дәлелдеуі. Норманың және скаляр көбейтіндінің анықтамасы бойынша:

(3) Коши теңсіздігін ескерсек, онда
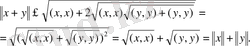
Теорема дәлелденді.
Ескерту.
. Егер
х, у
векторлары сызықты тәуелді болса:
х =
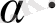 у,
онда (4. 3) теңсіздігі теңдікке айналады:
у,
онда (4. 3) теңсіздігі теңдікке айналады:
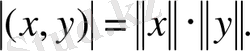
Шынында да,
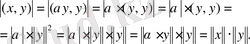
2. Егер
х, у
векторлары сызықты тәуелсіз болса:
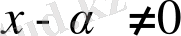 , онда (4. 4) теңсіздігі мына түрде жазылады:
, онда (4. 4) теңсіздігі мына түрде жазылады:
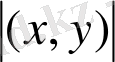 <
<
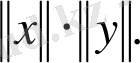
Шынында да,
х-
 у
у
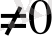 векторы үшін:
векторы үшін:
(х
-
 у, х -
у, х -
 у) >
0 немесе
(х, х) - 2
у) >
0 немесе
(х, х) - 2
 (х, у) +
(х, у) +
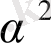 (у, у) >
0,
(у, у) >
0,
Бұдан
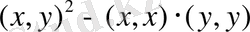 <0 немесе
<0 немесе
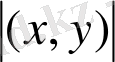 <
<

Ескерту. Егер х және у векторлары бағытталған кесінділер болса, онда (4. 4) үшбұрыш теңсіздігінен шығатын қорытынды: үшбұрыштың бір қабырғасының ұзындығы оның басқа екі қабырғасының ұзындықтарының қосындысынан кіші.
Нақты евклид кеңістігінде берілген екі
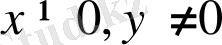 векторлардың арасындағы
векторлардың арасындағы
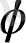 бұрышты
бұрышты
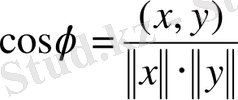 (4. 5)
(4. 5)
формуламен анықтауға болады.
Егер
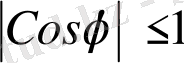 теңсіздігін ескерсек, онда (4. 5) формуладан Коши теңсіздігін аламыз.
теңсіздігін ескерсек, онда (4. 5) формуладан Коши теңсіздігін аламыз.
Теорема.
Егер берілген
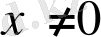 векторын кез келген нақты санға көбейтсек, онда
векторын кез келген нақты санға көбейтсек, онда
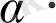 х
вектордың ұзындығы
х
вектордың ұзындығы
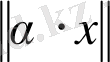 берілген
x
вектордың ұзындығы
берілген
x
вектордың ұзындығы
 мен
мен
 санының модулінің көбейтіндісіне тең:
санының модулінің көбейтіндісіне тең:
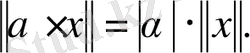
Дәлелд еуі. Нор ман ың анықт амасын ескерсек, онда
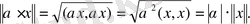 Теорема дәлелденді.
Теорема дәлелденді.
в) Ортонормалданған векторлар жүйесі және оның қасиеттері.
Анықтама. Егер евклид R кеңістігіндегі
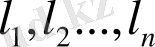 (4. 6)
(4. 6)
векторлар жүйесіне
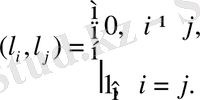
теңдіктері орындалса, онда (4. 6) векторларды ортонормалданған векторлар дейміз, егер (4. 7) теңдіктердің тек бірінші теңдіктері ғана орындалса, онда оны ортогоналды векторлар деп атаймыз.
Теорема.
Нөлдік вектор кез келген векторға ортогонал:
(х,
0) = 0,
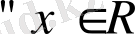 .
.
Дәлелдеуі
.
Кез келген
у
 векторға
(х, у)
= 0 теңдеуі орындалсын делік. Дәлелдеу керек
х=0
.
у
=
х
болғанда
(х, х) =0
. Бұдан
х
= 0. Теорема дәлелденді.
векторға
(х, у)
= 0 теңдеуі орындалсын делік. Дәлелдеу керек
х=0
.
у
=
х
болғанда
(х, х) =0
. Бұдан
х
= 0. Теорема дәлелденді.
Теорема (Пифагор) . Егер х, у векторлары ортогонал болса: (х, у) = 0, онда
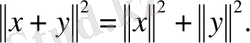
Дәлелдеуі
.
Егер
(х, у) =0
болса, онда (4. 5) формуладан соs
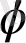 = 0, яғни
= 0, яғни
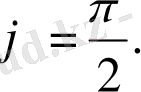 Ендеше
х, у
векторлары бір-біріне перпендикуляр:
х
Ендеше
х, у
векторлары бір-біріне перпендикуляр:
х
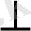 у.
Олай болса,
у.
Олай болса,
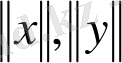 тік бұрышты үшбұрыштың катеттері,
тік бұрышты үшбұрыштың катеттері,
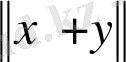 оның гипотенузасы ретінде қарастырылады. Норманың анықтамасы бойынша:
оның гипотенузасы ретінде қарастырылады. Норманың анықтамасы бойынша:
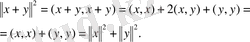
Теорема дәлелденді.
Теорема.
Ортонормалданған
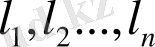 векторлар жүйесі сызықты тәуелсіз.
векторлар жүйесі сызықты тәуелсіз.
Дәлелдеуі . Берілген векторлардың сызықты тәуелсіз екенін дәлелдеу үшін
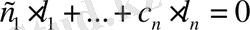 (4. 8)
(4. 8)
теңдеуді қарастырып, оның тек
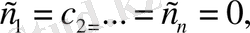 болғанда ғана орындалатынын дәлелдесек жеткілікті. Ол үшін (4. 8) теңдеудің екі жағында
l
болғанда ғана орындалатынын дәлелдесек жеткілікті. Ол үшін (4. 8) теңдеудің екі жағында
l
 векторына скаляр көбейтелік, яғни:
векторына скаляр көбейтелік, яғни:
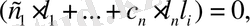
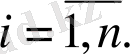
Осыдан
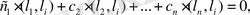
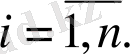
i
-дің біртіндеп 1, 2, . . . ,
n
мәндерін қабылдағанын және
 ортонормалданған векторлар екенін ескерсек, онда
ортонормалданған векторлар екенін ескерсек, онда
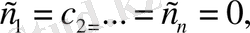 . Теорема дәлелденді.
. Теорема дәлелденді.
Теорема
.
Егер евклид
R
кеңістігіндегі

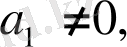
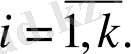 сызықты тәуелсіз векторлар жүйесі болса, онда оған сызықты тәуелді
сызықты тәуелсіз векторлар жүйесі болса, онда оған сызықты тәуелді
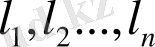 ортогоналды векторлар жүйесі мына төмендегі
ортогоналды векторлар жүйесі мына төмендегі
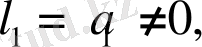
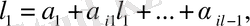
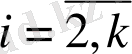 (4. 9)
(4. 9)
формулалармен өрнектеледі, мұндағы
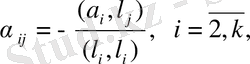
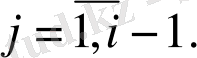 (4. 10)
(4. 10)
Дәлелдеуі.
Теореманы индукция әдісімен дәлелдейміз. Іздеп отырған
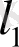 векторын берілген
векторын берілген
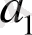 векторға тең деп аламыз:
векторға тең деп аламыз:
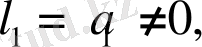 ал
ал
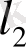 векторды
векторды
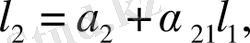 (4. 11)
(4. 11)
теңдеуінен анықтаймыз, мұндағы
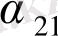 белгісіз тұрақты коэффициент. Егер
белгісіз тұрақты коэффициент. Егер
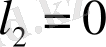 болса, онда
болса, онда
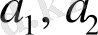 векторлары сызықты тәуелді, ал бұл теореманың шартына қарама қайшы, себебі
векторлары сызықты тәуелді, ал бұл теореманың шартына қарама қайшы, себебі
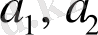 сызықты тәуелсіз. Сондықтан,
сызықты тәуелсіз. Сондықтан,
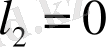 . Белгісіз
. Белгісіз
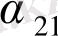 коэффициентті табу үшін (4. 11) тендікті
коэффициентті табу үшін (4. 11) тендікті
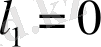 векторына скаляр көбейтеміз:
векторына скаляр көбейтеміз:
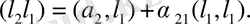
Іздеп отырған
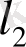 вектор белгілі
вектор белгілі
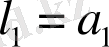 векторына ортогонал болу керек:
векторына ортогонал болу керек:
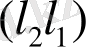 = 0. Онда
= 0. Онда
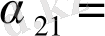
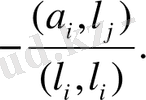
Сонымен, (4. 9), (4. 10) формулалардың i = 2, j=1 тең жағдайлары дәлелденді.
 ортогонал векторларын (4. 9) -дан, оның
ортогонал векторларын (4. 9) -дан, оның
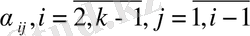 коэффициенттерін (4. 10) формуламен өрнектелетіндей етіп
коэффициенттерін (4. 10) формуламен өрнектелетіндей етіп
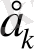
 векторын ізделік. Ол
е
к
векторды
векторын ізделік. Ол
е
к
векторды
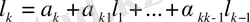 (4. 12)
(4. 12)
теңдігінсн анықтаймыз, мұндағы
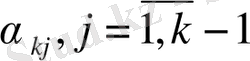 белгісіз тұрақты коэффициенттер. Егер
белгісіз тұрақты коэффициенттер. Егер
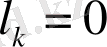 , онда
, онда
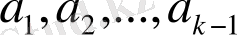 векторлары сызықты тәуелді, ал ол теореманың шартына қарама қайшы. Ендеше,
векторлары сызықты тәуелді, ал ол теореманың шартына қарама қайшы. Ендеше,
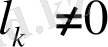 . Белгісіз
. Белгісіз
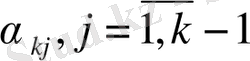 ,
тұрақты коэффициенттерді табу үшін, (4. 12) теңдеуді
,
тұрақты коэффициенттерді табу үшін, (4. 12) теңдеуді
 векторларына біртіндеп скаляр кебейтіп және
векторларына біртіндеп скаляр кебейтіп және
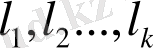 ортогонал векторлар екенін ескеріп, белгісіз
ортогонал векторлар екенін ескеріп, белгісіз
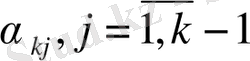 коэффициенттері (4. 10),
коэффициенттері (4. 10),
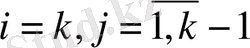 формулалардан анықталатынын дәлелдейміз. Теорема дәлелденді.
формулалардан анықталатынын дәлелдейміз. Теорема дәлелденді.
Жоғарыдағы теореманы дәлелдеу әдісін, яғни берілген сызықты тәуелсіз векторлар жүйесінен ортогоналды векторлар жүйесін құру әдісі, ортогонализациялау тәсілі деп аталады.
Теорема.
Егер евклид кеңістігіндегі
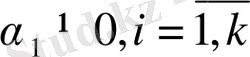 ортогоналды векторлар жүйесі болса, онда оған сызықты тәуелді
ортогоналды векторлар жүйесі болса, онда оған сызықты тәуелді
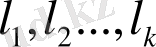 ортонормалданған векторлар жүйесін мына төмендегі
ортонормалданған векторлар жүйесін мына төмендегі
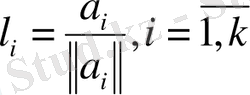 (4. 13) (4. 13)
(4. 13) (4. 13)
формулалармен өрнектеуге болады.
Дәлелдеуі
.
Теореманы дәлелдеу үшін (4. 13) формулалармен өрнектелген
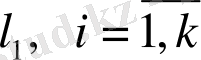 ортонормалданған векторлар жүйесі екенін дәлелдесек жеткілікті. Шынында да, егер
ортонормалданған векторлар жүйесі екенін дәлелдесек жеткілікті. Шынында да, егер
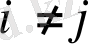 болса, онда:
болса, онда:
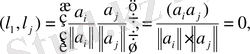
ал егер
i= j
болса, онда
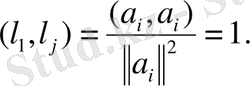
Теорема дәлелденді.
Теорема. Кез келген п ө лшемді евклид R кеңістігінде п вектордан құрылған ортонормалданған базис бар.
Дәлелдеуі.
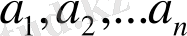 векторлар жүйесі евклид
R
кеңістігінің базисі болсын делік. Сондықтан, 4. 7-теорема бойынша
векторлар жүйесі евклид
R
кеңістігінің базисі болсын делік. Сондықтан, 4. 7-теорема бойынша
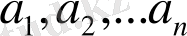 векторларына сызықты тәуелді
векторларына сызықты тәуелді
 ортогонал векторлар жүйесін құрамыз:
ортогонал векторлар жүйесін құрамыз:
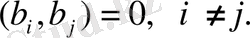 Енді 4. 8-теореманы пайдаланып,
Енді 4. 8-теореманы пайдаланып,
 векторларына сызықты тәуелді
векторларына сызықты тәуелді
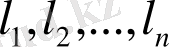 ,
ортонормалданған вектор жүйесін құрамыз, ал ол жүйе 4. 6-теорема бойынша сызықты тәуелсіз, яғни
,
ортонормалданған вектор жүйесін құрамыз, ал ол жүйе 4. 6-теорема бойынша сызықты тәуелсіз, яғни
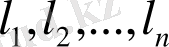 евклид
R
кеңістігінің ортонормалды базисі. Теорема дәлелденді.
евклид
R
кеңістігінің ортонормалды базисі. Теорема дәлелденді.
Мысал. [-1, 1] сегментте анықталған дәрежесі үштен аспайтын көпмүшеліктер кеңістігіндегі ортогонал базисті табалық.
Ортогонал базисті табу үшін
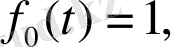
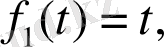
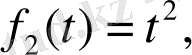
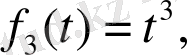 элементтерін базис ретінде қарастыралық. Енді 1,
элементтерін базис ретінде қарастыралық. Енді 1,
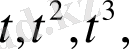 элементтеріне сызықты тәуелді
элементтеріне сызықты тәуелді
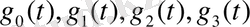 ортогонал базис ізделік. (4. 9) формула бойынша:
ортогонал базис ізделік. (4. 9) формула бойынша:
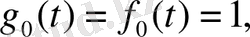
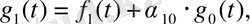
Мұндағы
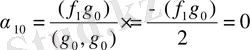 .
.
Сонымен,
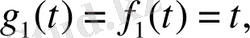
(. 9) формуладан
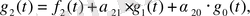
мұндағы
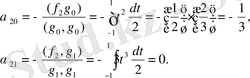
Сонымен,
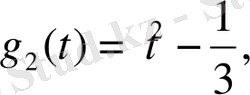
Ең соңында (4. 9) формуладан:
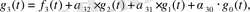
мұндағы
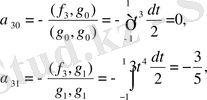
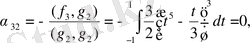
Сонымен,
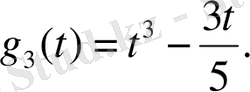
г) Ортонормалданған базисте координаттарымен өрнектелген екі вектордың скаляр көбейтіндісі
Теорема.
Евклид
R
п
кеңістігіндегі кез келген екі вектордың
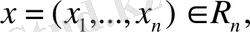
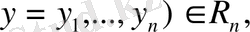 скаляр
көбейтіндісі
скаляр
көбейтіндісі
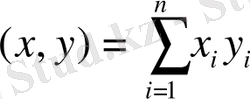 (1)
(1)
формуламен өрнектелу үшін, оның
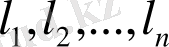 базисі ортонормалданған болуы қажетті әрі жеткілікті.
базисі ортонормалданған болуы қажетті әрі жеткілікті.
Қажеттілігі.
(4. 14) формула орындалсын деп,
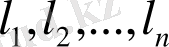 базис ортонормалданған болуын дәлелдейік.
х
пен
у
векторларын берілген базисте жіктелік:
базис ортонормалданған болуын дәлелдейік.
х
пен
у
векторларын берілген базисте жіктелік:
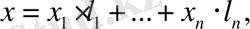
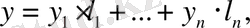
(4. 14) формуладан
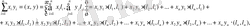 Соңғы теңдіктің орындалуы үшін евклид
Соңғы теңдіктің орындалуы үшін евклид
 кеңістіктің базисі ортонормалданған болуы жеткілікті:
кеңістіктің базисі ортонормалданған болуы жеткілікті:
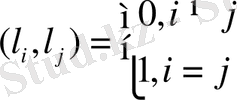
Жеткіліктігі.
Евклид
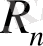 кеңістігінің
кеңістігінің
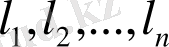 базисі ортонормалданған болсын деп ұйғарып, (1) формуланы дәлелделік. Ол үшін
х
пен
у
векторларыныд скаляр көбейтіндісін қарастырамыз:
базисі ортонормалданған болсын деп ұйғарып, (1) формуланы дәлелделік. Ол үшін
х
пен
у
векторларыныд скаляр көбейтіндісін қарастырамыз:
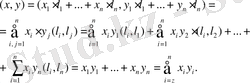
Теорема дәлелденді.
Теорема.
Евклид
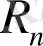 кеңістігіндегі
кеңістігіндегі
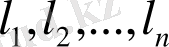 ортонормалданған базисте
ортонормалданған базисте
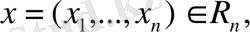 вектордың координаттары
вектордың координаттары
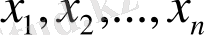 :
:
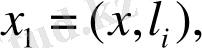
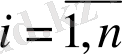 (4. 15)
(4. 15)
формуламен өрнектеледі.
Дәлелдеуі.
Берілген
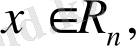 векторды
векторды
 базис бойынша жіктейік:
базис бойынша жіктейік:
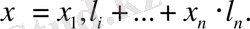
Осы жіктеудің екі жағында
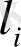 векторына скаляр көбейтсек және
векторына скаляр көбейтсек және
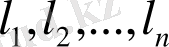 ортонормалданған векторлар жүйесі екенін ескерсек, онда
ортонормалданған векторлар жүйесі екенін ескерсек, онда
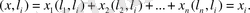
Теорема дәлелденді.
Анықтама.
Егер кез келген
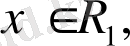 векторы кез келген
векторы кез келген
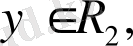 векторына ортогонал болса, яғни
(х, у) =
0, онда евклид
R
кеңістігінің екі ішкі
векторына ортогонал болса, яғни
(х, у) =
0, онда евклид
R
кеңістігінің екі ішкі
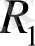 мен
мен
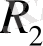 кеңістіктерін:
кеңістіктерін:
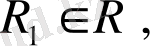
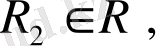 өзара ортогонал деп атаймыз, яғни
өзара ортогонал деп атаймыз, яғни
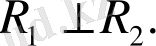
Теорема.
Евклид
R
кеңістігінің ішкі
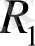 мен
мен
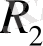 кеңістіктегі бір-бірімен ортогонал болу үшін, яғни
кеңістіктегі бір-бірімен ортогонал болу үшін, яғни
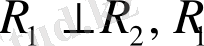 кеңістігінің барлық базистері
кеңістігінің барлық базистері
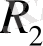 кеңістігінің барлық базистеріне ортогонал болуы қажетті әрі жеткілікті.
кеңістігінің барлық базистеріне ортогонал болуы қажетті әрі жеткілікті.
Қажеттілігі:
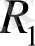 мен
мен
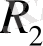 кеңістіктері өзара ортогонал болсын деп ұйғарайық, яғни
кеңістіктері өзара ортогонал болсын деп ұйғарайық, яғни
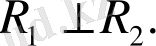 Онда анықтама бойынша
Онда анықтама бойынша
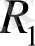 кеңістігінің барлық базистері
кеңістігінің барлық базистері
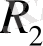 кеңістігінің барлық базистеріне ортогонал болады.
кеңістігінің барлық базистеріне ортогонал болады.
Жеткіліктілігі:
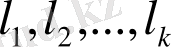 векторлар жүйесі
векторлар жүйесі
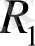 кеңістігінің базисі, ал
кеңістігінің базисі, ал
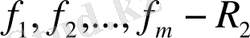 кеңістгінің базисі болсын және
кеңістгінің базисі болсын және
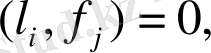
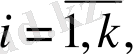
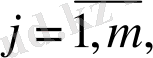 теңдіктері орындалсын деп есептелік. Енді кез келген
теңдіктері орындалсын деп есептелік. Енді кез келген
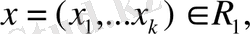
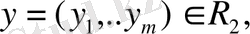 векторлардың сәйкес базистерде жіктеулерін
векторлардың сәйкес базистерде жіктеулерін
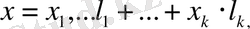
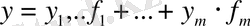
алып, олардың скаляр кебейтіндісін қарастыралық. Онда
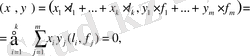
яғни кез келген
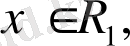
 векторлары ортогонал немесе
векторлары ортогонал немесе
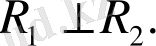 Теорема дәлелденді.
Теорема дәлелденді.
Теорема.
Егер евклид
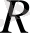 кеңістігінің екі ішкі
кеңістігінің екі ішкі
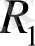 мен
мен
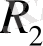 кеңістіктері өзара ортогонал болса:
кеңістіктері өзара ортогонал болса:
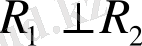 онда олардың қиылысуы нөл вектор болады:
онда олардың қиылысуы нөл вектор болады:
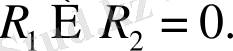
Дәлелдеуі.
Кез келген
х
вектор
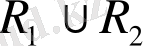 кеңістігінің элементі болсын деп ұйғаралық, яғни
кеңістігінің элементі болсын деп ұйғаралық, яғни
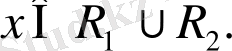 Онда
Онда
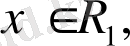
 және
(х, х)
= 0. Бұдан
х
= 0. Теорема дәлелденді.
және
(х, х)
= 0. Бұдан
х
= 0. Теорема дәлелденді.
Айталық, евклид
R
кеңістігінің кез келген ішкі
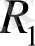 кеңістігі берілсін:
кеңістігі берілсін:
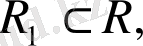 ал
ал
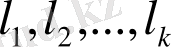 оның ортонормалданған базисі болсын делік. Енді ол базисті евклид
оның ортонормалданған базисі болсын делік. Енді ол базисті евклид
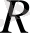 кеңістігінің ортонормалданған базисіне дейін толықтыралық, яғни
кеңістігінің ортонормалданған базисіне дейін толықтыралық, яғни
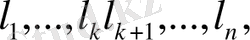 мұндағы
п - diт R, k
= dim
мұндағы
п - diт R, k
= dim
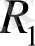 .
.
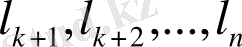 векторлар жүйесі евклид
R
кеңістігінің өлшемі (n - k) -ға тең ішкі
векторлар жүйесі евклид
R
кеңістігінің өлшемі (n - k) -ға тең ішкі
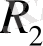 кеңістігін құрастырады, яғни
кеңістігін құрастырады, яғни
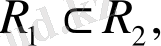
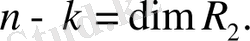
Теорема.
Егер кез келген
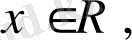 вектор ішкі
вектор ішкі
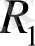 кеңістігінің кез келген векторына ортогонал болса:
кеңістігінің кез келген векторына ортогонал болса:
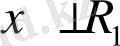 , онда
х
ішкі
, онда
х
ішкі
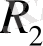 кеңістігінің векторы:
кеңістігінің векторы:
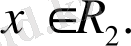
Дәлелдеуі.
Теореманың шарты бойынша
 және
және
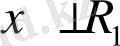 , яғни
, яғни
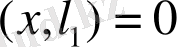 ,
,
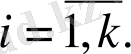
Енді
х
вектордың жіктелуінің екі жағында
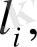
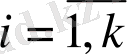 векторларына біртіндеп скаляр көбейтелік:
векторларына біртіндеп скаляр көбейтелік:
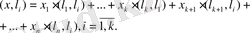
Егер
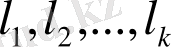 ортонормалданған векторлар және
ортонормалданған векторлар және
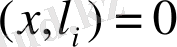 екенін ескерсек, онда
екенін ескерсек, онда
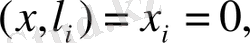
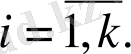
Демек, х вектордың жіктелуі мына түрде жазылады:
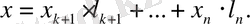
Бұдан,
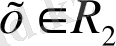 .
Теорема дәлелденді.
.
Теорема дәлелденді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz