Электрониканың физикалық негіздері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

Лекциялардың қысқаша конспектісі

Лекция - 1,2
Қатты денелердің зоналар теориясы

Қатты денелер атомдардан тұрады, яғни ядро мен электрондардан. Атомдардың ядросы кристалл торларды (решеткаларды) құрастырды. Бұл кристалл торларды құраушы атомдардың ядросы, бірінен кейін бірі тәртіпті орналасады. Егер бұндай кристалл торды электр өрісіне орналастыратын болсақ, олар кристалл торда орналасқан атомдардың ядролары зарядталғанына қарамастан деформацияланбайды, яғни өзінің бастапқы қалпын сақтайды. Себебі атомдардың ядроларын кристалл тордың түйінінде ұстап тұрған күштер, электр өрісінің әсер күшінен көп үлкен. Бірақ атомдардың ядросына, әлсіз байланыстығы электрондар, қатты дене ішінде қозғалыста болып электр тоғын туғызады. Бұл құбылыстарды түсіндіруде біраз қиыншылықтар туындайды. Себебі электрондар зарядқа ие және қозғалысы кезінде бір-бірімен әсерлеседі. Электрондар теріс зарядқа ие болуына байланысты олар бір-бірін тебеді. Сол себепті электрондардың қозғалысы оны қоршаған электрондардың қозғалысына байланысты болады. Мұндай жағдайда бір электронның қозғалысын есептеп қоймай, көп электронның қозғалысын есептеуге тура келеді. Сол себепті атом ядросының және электрондардың қатты денелердегі стационар күйін және энергетикалық спектрлерін анықтау үшін Шредингер теңдеуін шешуге тура келеді.
Шредингер теңдеуі: НФ=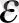Ф (1), мұнда Н - кристаллдың гамильтоны, Ф-гамильтонның меншікті толқын функциясы, 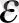-кристаллдың энергиясы.
Кристаллдың толқындық функциясының мәні барлық электрондардың координаталары ri және барлық атомдардың ядроларының координаталары Ri байланысты болады, яғни Ф=Ф(r1, r2, r3 ... .. rn, R1, R2, R3 ... ... Rn) (2)
Гамильтон операторы мына операторларды қарастырады: 1) электрондардың кинетикалық энергиясының операторы
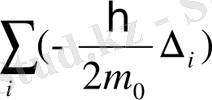, мұнда 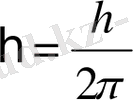Планк тұрақтысы. m0 - электронның массасы,
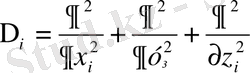- Лаплас операторы деп аталады, і - электрондар саны.
2) ядроның кинетикалық энергиясының операторы

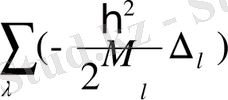, мұнда 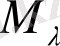-ядро масасы,
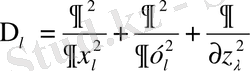
3) электрондардың жұптық әсерлесуінің потенциал энергиясы
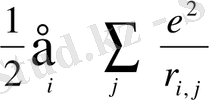, мұнда е- электрон з-ды, ri және rj - жұп электрондардың координаторлары, 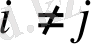тең болмайды.
4) ядролардың жұптық әсерлесуінің потенциал энергиясы
U0 (R1, R2, R3... Rn)
5) Электрондардың ядролармен әсерлесуінің потенциал энергиясы
U (r1, r2, ... ..rn, R1, R2 ... ...Rn ) Гамильтониканың жоғарыда көрсетілген құраушыларын есепке алатын болсақ Шредингер теңдеуі мына көрініске ие болады:

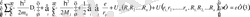
(3) теңдеудегі тәуелсіз өзгерушілердің саны 1 см3 кристаллдағы бөлшектер саны 1023 - бөлшектерге шамалас болады. Сол себепті осындай сандағы теңдеулерді шешу өте қиынға соғады. Бірақ көптеген жеңілдіктер беру арқылы бұл теңдеулерді жалпы түрде жуықтап шешуге болады. Бұл теңдеулерді дәл шешу әдісі жоқ, сол себепті бұл теңдеулерді бір электронды бөлшек үшін қолданады. Бір электронды бөлшекті қолдану әдісі қатты денелердң зоналар теориясына алып келеді. Зоналар теориясының негізінде адиабаталық жақындау принципі жатыр.
Кванттық механикалық жүйе ауыр ядро және жеңіл электрон бөлшектерге бөлінеді. Ядролар кристалл тордың түйінінде қозғалмайды, ал электрон тұрақты ядролар өрісінде қозғалыста болады деп қарастырылады. Осылайша зоналық теория бойынша электрон ядролардың сыртқы өрісінде қозғалыста болады деп, көп электрондық есептеулерді бір электрондық есептеуге алмастыруға болады. Егер қатты дене оқшауланған атомдардан тұрады деп қарастырсақ, олардың энергетикалық деңгейлері бір-біріне дәл келеді. (1-сурет). Ал атомдарды бір-біріне жақындататын болсақ, олардың арасындағы ара-қашықтық қатты денелерді құраушы атомдардың арасындағы арақашыққа жақындай бастағанда атомдардың энергетикалық деңгейлері ығысып ажырай бастайды және зоналарға бөлінеді де зоналық энергетикалық спектрлер пайда болады.
Е
0 r

1-сурет

Қатты денелерде зоналық энергетикалық спектрдің пайда болуы кванттық-механикалық эффект болып есептеледі.
Кристаллдарда (қатты денелерде) валенттік электрондар атомдармен әлсіз байланыста болады (ішкі электрондарға салыстырғанда). Сол себепті валентті электрондар бір атомнан екінш атомға өте алады. Сыртқы электрондардың энергетикалық мәні 1-суретте штрихталған энергетикалық мәндерге сәйкес келеді. Штрихталған энергетикалық мәндерді рұқсат етілген зоналар мәні деп атайды. Рұқсат етілген зоналардың мәні, рұқсат етілмеген энергетикалық зонамен ажыратылған болады. Рұқсат етілмеген зонада электрондар болмайды. Рұқсат етілген және рұқсат етілмеген зоналардың ені кристаллдардың өлшеміне байланысты болмайды. Рұқсат етілген зонаның ені валенттік электрондардың байланыс энергиясына тәуелді. Валенттік электрондардың ядромен байланыс энергиясы қанша кіші болса, рұқсат етілген зонаның ені сонша енді болады.

Лекция 3, 4
Металл, диэлектрик және жартылай өткізгіштердің зоналар теориясы

Қатты денелердің зоналар теориясы металлдардың (өткізгіштердің), диэлектриктердің (изоляторлардың) және жартылай өткізгіштердің болуын түсіндіріп береді. Қатты денелердің металл (өткізгіш), диэлектрик (изолятор) және жартылай өткізгіш болуы, зоналар теориясындағы рұқсат етілмеген (тыйым салнған) зонаның энергетикалық мәніне (еніне) байланысты болады.
Зонадағы энергетикалық деңгейлердің электрондармен толтырылуы, атомдық деңгейлердің электрондармен толтырылуына байланысты. Атомдардың энергетикалық зоналары валенттік зона деп аталады. Валенттік зоналар электрондармен барлық уақытта толық болады. Валенттік зонадан соң рұқсат етілмеген (тыйым салынған) зона орналасады. Рұқсат етілмеген зонадан соң рұқсат етілген, яғни өткізгіштік зона орналасады. Өткізгіштік зона электрондармен белгілі бір деңгейде толтырылған немесе бос болуы мүмкін. Зонаның электрондармен толу дәрежесіне байланысты тыйым салынған зонаның енінің көрінісі
1 суретте келтірілген.
а) б) в) г)
өткізгіштік зона
өткізгіштік зона
өткізгіштік зона
өткізгіштік зона
Белгілі бір дәрежеде толтырылған зона
Валенттік зона
Валенттікзона
Валенттік зона
өткізгіштік зона
өткізгіштік зона
өткізгіштік зона
өткізгіштік зона
Белгілі бір дәрежеде толтырылған зона
Валенттік зона
Валенттікзона
Валенттік зона
Металл (өткізгіш) Металл Жартылай өткізгіш Диэлектрик
1-сурет

1а - суретте валенттік зонаның ең жоғарғы деңгейі электрондармен белгілі бір дәрежеде толған, бірақ бос орындар бар. Сол себепті электрондар қандай да бір энергия алатын болса (жылулық немесе электр өрісі әсерінен)ол өткізгіштік зонаның бос жоғарғы деңгейіне өте алады. Нәтижеде еркін электрон болып электр өткізгіштікке қатыса алады. Мұндай жағдай металлдарда болады (1а-сурет). Қатты дене электр тоғын жақсы өткізеді, егер валенттік зона өткізгіштік зонамен қилысатын болса (1б-сурет). Кейбір қатты денелер электрондармен толық толған валенттік зонадан және еркін зонадан (өткізгіштік зонадан) тұрады. Бұл екі зона тыйым салынған зонамен ажыратылған болады.
Мұндай қатты денлер тыйым салынған зонаның энергетикалық мәніне байланысты диэлектрик (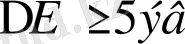) болады.
Егер тыйым салынған зонаның ені 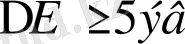үлкен болса онда валенттік зонадан өткізгіштік зонаға, денені қыздыру арқылы немесе электр өрісінің әсерімен электрондарды өткізгіштік зонаға өткізу мүмкін емес. Сол себепті диэлектриктерде өткізгіштік зонада еркін электрондар болмайды. Бұл дегеніміз диэлектрик электр тоғын өткізбейді. Ал жартылай өткізгіштерде тыйым салынған зонаның, энергетикалық мәні 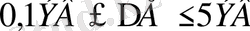болады. Сол себепті жартылай өткізгіштерді қыздыру немесе электр өрісін қою арқылы валенттік зонадан өткізгіштік зонаға электрондарды орын ауыстыру мүмкін. Олай болса жартылай өткізгіштер электр тогын өткізе алады.

Лекция -5, 6
Жартылай өткізгіштің электр өткізгіштігінің қарапайым теориясы

Жартылай өткізгіштің электр өткізгіштігінің қарапайым теориясын түсіну үшін донорлы жартылай өткізгіш аламыз, яғни заряд тасымалдаушылар электрондар. Электрондарды идеал бөлшектер деп қарастырамыз, яғни электрондардың өзінің меншікті көлемі жоқ және олар бір-бірімен әсерлеспейді.
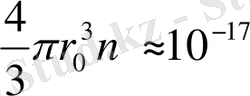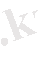
Классикалық теория бойынша электрон радиусы ro10-13cм, онда егер электрондардың концентрация n=1023cм-3 болғанда электрондардың көлемі болып заттың негізгі көлемінің 10-17 бөлігіне ие болады. Сол себепті бұл көлемді есепке алмасақ болады. Мысалы электрондардың концентрациясы 1 см3-та n-болсын, ал олардың дрейфтік қозғалысының жылдамдығы 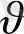-болсын. Онда электрондар тасымалдайтын тоқтың тығыздығы тең болады (1)
Электрондардың дрейф жылдамдығын анықтау үшін олардың соқтығысуының ықтималдығы dt- болсын. Олай болса n- бөлшектердің (электрондардың) dt- уақытта соқтығысу ықтималдығы тең болады n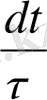. Онда берілген бағытта заряд тасымалдаушы бөлшектер dt - уақытта соқтығысып шашырауы нәтижесінде мынадай шамаға кемиді, яғни - 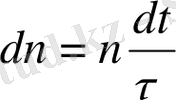(2).
(2) - теңдеуді шешетін болсақ, онда t- уақытта соқтығыспайтын электрондардың санын табамыз: 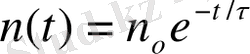(3), мұнда болады, 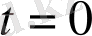болғанда. (3)- теңдеу көрсетеді белгілі бағытта қозғалыстағы электрондардың саны экспоненциалдық заң бойына тұрақты шама уақытымен кемитінін. Тұрақты шама -ды анықтау үшін біз х-осі өріс бағытымен бағыттас деп қарастырып t=0 болғанда барлық электрондар соқтығысады деп есептейміз, бұдан соң х-осі бағыты бойынша электрондар дейфті қозғалыста болып 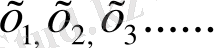аралықты басып өтсін, бұл кездегі уақыт 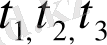... ... ... болсын. Онда барлық басып өткен арақашықтық тең болады: 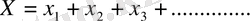болады.
Ал кеткен уақыт T= t1+t2+t3+ ... ... ... . болады.
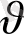
Дрейф жылдамдық электрондардың бағытталған қозғалысының жылдамдығы. Ол тең болады: 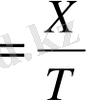(4).
Егер no-электрондардың еркін қозғалысының орташа уақыты 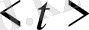- болса, онда 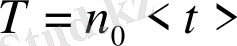болады (5).
Бір жағынан электрондардың біраз бөлігінің еркін қозғалысының орташа уақыты t-ға тең болады. Онда олардың саны 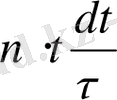-болады. Ал жалпы уақыт Т-ны 0 ден 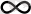дейін интегралдап табуға болады, яғни: 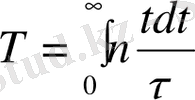(6).
(5), (6) және (3) теңдеулерді пайдаланып еркін қозғалыстың орташа уақыты былайша анықталады: 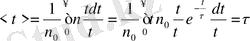(7). Олай болса еркін қозғалыстың орташа уақыты, яғни екі соқтығысуға кететін уақыттың орташасы. Электр өрісінің кернеулігі Е, m-массалы электронға үдеу береді, яғни 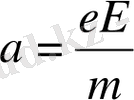(8). Электрон еркін қозғалу уақыты t-да мынадай жылдамдыққа ие болады: 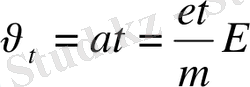(9)
Ал басып өткен аралық тең болады: 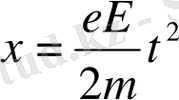(10). Барлық электрондардың басып өткен аралығының жиындысы тең болады.
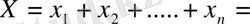
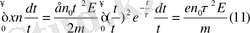Олай болса дрейф жылдамдық тең болады, яғни 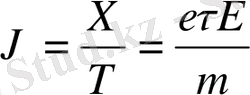(12). (12) теңдеу көрсетеді дрейф жылдамдықтық электр өрісінің кернеулігіне тура тәуелділігін, ал электронның массасына кері тәуелділігін. Дрейф жылдамдықты электр өрісінің кернеулігіне байланыстырушы шаманы зарядтардың қозғалғыштығы (подвижность) деп атайды. Зарядтардың қозғалғыштығын μ- деп белгілейміз. 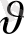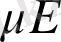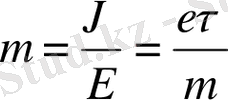Онда зарядтардың жылдамдығы тең болады: = (13), бұдан 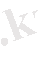(14). келіп шығады. Олай болса зарядтардың қозғалғыштығы бірлік электр өрісіндегі зарядтардың жылдамдығына тең екен. (14) және (1) теңдеулерді пайдаланып тоқ тығызды j 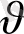=-en=en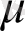E (15) екенін көреміз. 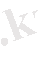Ом заңына сәйкес меншікті өткізгіштік тең: 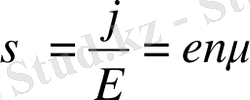(16). Онда (14) есепке алып меншікті өткізгіштік тең болады: 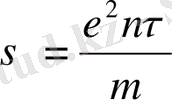(17). Егер 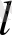= 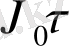екенін есепке алсақ онда (17) теңдеуді былайша жазуға болады. 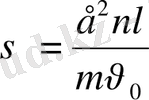(18), мұнда 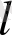- еркін жүру жолының орташа ұзындығы, 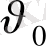- жылулық қозғалысының орташа жылдамдығы.
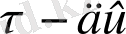анықтауда электронның толық жылдамдығын есепке алу керек. Себебі толық жылдамдық жылулық жылдамдық 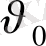және дрейфті жылдамдық 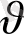- мен анықталады. Олай болса 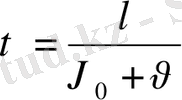(19) екені келіп шығады. Мұнда еркін қозғалыстағы уақыттың орташасы, яғни екі соқытығысудың орташа уақыты.

Лекция - 7,8
Меншікті жартылай өткізгіштің электр өткізгіштігі

Жартылай өткізгіштер табиғатта Менделеев жүйесінің ІV, V, VI химиялық элементтері ретінде кездеседі. Мысалы Si, Ge, As, Se, Te және олардың қоспалары ретінде. Жартылай өткізгіштер меншіктері қоспасыз және қоспалы жартылай өткізгіштер болып бөлінеді. Меншікті қоспасыз жартылай өткізгіштер болып химиялық таза жартылай өткізгіштер есептеледі. Олар Si, Ge, InSb, GaAs, Cd және басқалар. Ноль градус Кельвинде, егер басқа сыртқы әсерлер болмаса меншікті жартылай өткізгіш диэлектрик болады, яғни электр тогын өткізбейді. Ал егер меншікті жартылай өткізгіштің температурасын жоғарылататын болсақ валенттік зонаның жоғарғы деңгейінде орналасқан электрондар, өткізгіштік зонаның төменгі деңгейіне көшіп өтеді. (1-сурет).

ІІ өткізгіштік зона

тиым салынған

І валенттік зона

1- сурет

Осындай меншікті жартылай өткізгішке электр өрісін қойатын болсақ көшіп өткен
электрондар электр өрісіне қарсы қозғалысқа келеді, яғни электр тогы пайда болады. Осылайша өткізгіштік зона заряд тасымалдауға қатысады. Меншікті жартылай өткізгіштің өткізгіштік зонасында электрондардың заряд тасымалдауын электрондық өткізгіштік немесе n-типті өткізгіштік деп атайды. Жылулық әсері нәтижесінде валенттік зонадан өткізгіштік зонаға электронның көшіп өтуі нәтижесінде валенттік зонада бос орын пайда болады. Бұл бос орынды кемтік деп атайды. Электр өрісі әсері нәтижесінде бос орынға (кемтікке) көрші электрон өтеді. Осылайша кемтіктердің бағытталған қозғалысы пайда болады. Бұл бағытталған қозғалыс электрондардың қозғалыс бағытына қарама-қарсы болады. Бос орынның, яғни кемтіктің заряды электрон зарядына тең, ал таңбасы қарама-қарс. Меншікті жартылай өткізгіштің бағытталған кемтіктер қозғалысынан пайда болған өткізгіштігін, кемтіктік өткізгіштік немесе р-типті өткізгіштік деп атайды. Сонымен меншікті жартылай өткізгіште өткізгіштіктің екі механизмін көруге болады, яғни электронды және кемтікті.
Өткізгіштік зонадағы электрондрдың саны, валенттік зонадағы кемтіктердің санына тең болады, яғни ne=np (1), мұнда ne- электрондардың саны, np- кемтіктердің саны.
Жартылай өткізгіштердің өткізгштігі барлық уақытта қоздырылған өткізгіштік болады. Қоздырушы фактор болып температура, жоғары электр өрісі немесе сәулелендіру есептеледі.
Меншікті жартылай өткізгіштерде Ферми деңгейі тиым салынған зонаның ортасында орналасқан болады. (2-сурет).

өткізгіштік зона
Е2

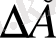
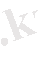
ЕF -------------------------- тиым салынған зона

Е1

валенттік зона
2- сурет
Валенттік зонаның жоғарғы деңгейінде орналасқан электронды, өткізгіштік зонаның төменгі деңгейіне өткізу үшін электронға қоздыру энергиясы жұмсалады. Ол қоздыру энергиясының мәні тиым салынған зонаның энергетикалық мәніне 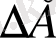-ге тең, не одан көп болуы керек. Жоғарыда айтылғандай электрон өткізгіштік зонаға өткен кезде валенттік зонада кемтік пайда болады. Сол себепті қоздыру энергиясы тең екі бөлікке бөлінуі керек. Олай болса меншікті жартылай өткізгіштің тиым салынған зонасының ортасында орналасқан Ферми деңгейінің энергиясы бір уақытта электронды және кемтікті қоздыруға керек энергия екен.
Жартылай өткізгіштердің өткізгіштік зонасындағы электрондардың концентрациясы мына теңдеумен анықталды:
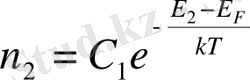(2), мұнда С1- тұрақты шама, ол температураға және электронның эффектив массасына байланысты болады. Е2- өткізгіштік зонаның төменгі деңгейіне тура келетін энергия, ЕF - Ферми деңгейінің энергиясы, Т-термодинамикалық температура. Валенттік зонадағы кемтіктердің концентрациясын мына теңдеумен анықтайды: 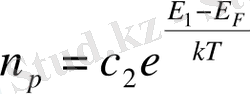(3), мұнда С2 - тұрақты шама, ол температураға және кемтіктің эффектив массасына байланысты болады. Е1- валенттік зонаның жоғарғы деңгейіне сай келетін энергия. Меншікті жартылай өткізгіштерде 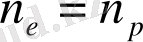болады. Онда 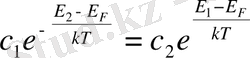(4), екені келіп шығады. Егер электрондар және кемтіктердің эффектив массасы mp=mn, болса, онда С1=C2 болып, бұдан
- (Е2-ЕF)=E1-EF болып, онда 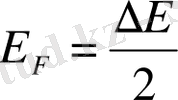келіп шығады. Бұл дегеніміз меншікті жартылай өткізгіштерде Ферми деңгейі шынында да тиым салынған зонаның ортасында жатады. Меншікті жартылай өткізгіштерде 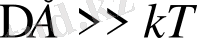болуына байланысты Ферми-Дирик теңдеуі Ni= 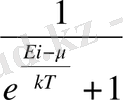(5), мұнда Еі - энергияның кванттық күйі, 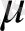-химиялық потенциал. Максвелл-Больцман теңдеуіне айналады N(E) 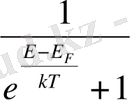(6) теңдеуге 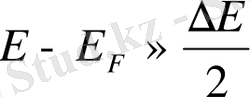мәнін қойсақ, онда Максвелл Больцман теңдеуі N(E) 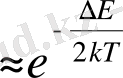(7) болады.
N(E)- өткізгіштік зонаға өткен электрондардың, сонымен бірге пайда болған кемтіктердің санына тәуелді болады. Сонымен меншікті - жартылай өткізгіштің меншікті өткізгіштігі тең болады: 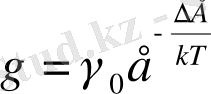(8),мұнда 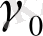тұрақты шама, ол жартылай өткізгішке байланысты.
Температураны арттырумен жартылай өткізгіштің өткізгіштігінің артуы тек жартылай өткізгіштерге тән қасиет. Мысалы металдарда температура артуымен оның өткізгіштігі кемиді. Жартылай өткізгіштердің температура артуымен өткізгіштігінің артуын зоналық теория бойынша былайша түсіндіруге болады, яғни температура артқанда валенттік зонадан өткізгіштік зонаға өткен электрондардың саны артып барады да, бұл электрондар заряд тасымалдауға қатысады, нәтижеде жартылай өткізгіштің өткізгіштігі артады.
Егер ln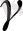-ның 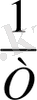байланысты графигін қарастыратын болсақ меншікті жартылай өткізгіштер үшін 1-суретте көрсетілгендей түзу сызық болады. Осы түзу сызықтың бұрышы арқылы 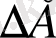-ні анықтауға болады. Түзу сызықтың ln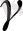-мен қилысатын жері ln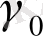- береді.
ln

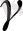
ln

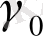
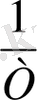
Жартылай өткізгіштерде электрондар мен кемтіктердің генерациясынан (пайда болуынан) басқа электрондар мен кемтіктердің рекомбинациясы (жойылуы) болуы мүмкін. Оның себебі болып кейбір электрондар өткізгіштік зонадан валенттік зонаға өзінен энергия шығаруы нәтижесінде қайтып түседі. Нәтижеде белгілі бір температурада валенттік зонадан өткізгіштік зонаға өткен электрондар мен өткізгштік зонадан валенттік зонаға қайтып түскен электрондр арасында тепе-теңдік орнайды. Бұл кездегі электрондар саны (7) теңдеумен анықталады.

Лекция - 9,10
Қоспалы жартылай өткізгіштердің электр өткізгіштігі

Жартылай өткізгіштердің электр өткізгіштігі қоспалар арқылы орындалатын болса, бұл өткізгіштікті қоспалы өткізгіштік деп, ал жартылай өткізгіштің өзін қоспалы жартылай өткізгіштік деп атайды. Қоспалы өткізгіштік жартылай өткізгіштерге ендірілген қоспалар арқылы немесе түрлі ақаулар арқылы жүзеге асырылады. Қоспа болып басқа элементтің атомы, ақау, бос түйіндер немесе түйіндер арасындағы атомдар есептеледі. Жартылай өткізгіште қоспа болатын болса, онда олар оның өткізгіштігін қатты өзгертіп жібереді. Мысалы кремнийге 0,001% бор атомын ендіретін болсақ, бұл қоспа кремнийдің өткізгіштігін 106 - есе арттырып жібереді.
Жартылай өткізгіштің қоспалы өткізгіштігін қарастыруды кремний (Si) және германий (Ge) арқылы қарастырайық. Бұларға негізгі атомның валенттілігінен бір валенттілікке айырмашылығы бар элемент ендірейік. Мысалы германийдің бір атомын, бес валенттік электроны бар мышьякпен (As) алмастырайық (1а сурет). Бұл кезде мышьяктің бір электроны байланыста болмай қалады. Бұл байланыста болмаған электрон өте оңай атомнан ажыралып еркін электрон болып қалады. Еркін электронның пайда болуы германийде коваленттік байланысты бұзбайды және бұл кезде кемтік пайда болмайды.

а)

б)

D
A

1-сурет 2-сурет

Зоналық теория бойынша жоғарыдағы процесстерді былайша қарастыруға болады (2б-сурет). Жартылай өткізгішке қоспа енгізетін болсақ ол, кристалл решетканың өрісін өзгертеді, нәтижеде тиым салыған зонада қоспа мышьяктың валенттік электрондарының энергетикалық деңгейі D-пайда болады. Бұл деңгей D-ны қоспаның донорлық энергетикалық деңгейі деп атайды. Сонымен негізгі атомның валенттік электронынан бір валенттік электронға артық қоспа жартылай өткізгішті n-типті жартылай өткізгішке айналдырып заряд тасымалдаушылар электрондар болады. Бұл кездгі өткізгіштікті электронды қоспалы өткізгіштік деп атайды, ол жартылай өткізгішті электронды жартылай өткізгіш деп атайды. Электронды қоспалы жартылай өткізгіштің электрон көзі болып, тиым салынған зонада пайда болған донорлық деңгей есептеледі.
Егер жартылай өткізгіш кремнийге (Si) үш валенттік электроны бар борды (В) ендіретін болсақ (2 а-сурет), негізгі атомдармен байланысқа кіру үшін бордың бір валенттік электроны жетіспейді, де бір байланыс бос қалады. Бұл бос қалған байланыс электронды көрші атомнан алуы мүмкін, онда көрші атомда электронның орнында бос орын яғни кемтік пайда болады. Бұл кемтікті оның көрші электроны толтыруы мүмкін, нәтижеде кемтіктің кристалл торда еркін орын ауыстыруын, яғни қозғалысын аламыз. Егер кемтіктің заряды электрон зарядына тең оң заряд екенін есепке алсақ, бұл кезде кемтік оң таңбалы заряд тасымалдаушы болады. Зоналық теория бойынша үш валентті қоспа бор кремнийдің решеткасының өрісін өзгертеді де тиым салынған зонаның төменгі бөлігінде акценторлық (А) энергетикалық деңгей туғызады. Бұл деңгейде электрон болмайды. Бұл акценторлық А-деңгейдің валенттік зонаға жақын орналасуына байланысты, төменгі температуралардың өзінде электрондар валенттік зонадан акценторлық деңгейге өте алады. Бірақ бұл электрондар заряд тасымалдауға қатыса алмайды. Себебі бұлар қоспа бор атомымен күшті байланыста болады. Заряд тасымалдаушылар болып валенттік зонадағы кемтіктер қызмет қылады. Бұл кемтіктер валенттік зонадағы электрондардың акценторлық деңгейге өтуінен пайда болған. Осылайша негізгі атомнан бір валенттік электроны кем қоспа жартылай өткізгіште кемтіктік өткізгіштік туғызады, бұл өткізгіштікті р-типті өткізгштік деп атайды. Кемтіктік өткізгіштікке ие жартылай өткізгішті, кемтікті жартылай өткізгіш деп атайды. Валенттік зонадан электрондарды тартып алатын энергетикалық деңгейлерді акценторлық энергетикалық деңгейлер деп атайды.
Меншікті жартылай өткізгіштерде өткізгіштік бір уақытта электрондармен және кемтіктермен заряд тасымалдау нәтижесінде болатын болса, ал қоспалы жартылай өткізгіштерде заряд тасымалдаушылар тек электрондар болады егер қоспа донор болса, ал қоспа акцентор болса заряд тасымалдаушлар тек кемтіктер болады. Донорлы қоспалы жартылй өткізгіш үшін негізгі заряд тасымалдаушылар электрондар, акценторлы қоспалы жартылай өткізгіш үшін негізгі заряд тасымалдаушылар кемтіктер. Кемтіктер донорлы қоспалы жртылай өткізгіш үшін негізгі болмаған заряд тасымалдаушыларға жатады, ал электрондар акценторлы қоспалы жартылай өткізгіш үшін негізгі болмаған заряд тасымалдаушыларға жатады.
Тиым салынған зонада қоспалардан пайда болған энергетикалық деңгейлер Ферми деңгейінің жағдайын өзгертеді.Есептеулер нәтижелері көрсетеді, Ферми деңгейі n- типті жартылай өткізгіштерде Т=О К температурада өткізгіштік зонамен донорлық деңгей ортасында жатады (3-сурет). Температураны жоғарылатқан сайын донорлық деңгейдегі электрондар өткізгіштік зонаға өте бастайды. Бұл электрондар заряд тасымалдауға қатысады. Бұндай жартылай өткізгішті n- типті жартылай өткізгіштер деп атайды. Ал р-типті жартылай өткізгіштерде Т=О К температурада Ферми деңгейі валенттік зонаның жоғарғы деңгейімен акценторлық деңгей ортасында жатады (4-сурет). Температураны жоғарылатқан сайын валенттік зонаның жоғарғы деңгейіндегі электрондар акценторлық деңгейге өте бастайды да, валенттік зонада кемтіктер артып барады. Нәтижеде бұндай жартылай өткізгіштерде заряд тасымалдаушылар кемтіктер болады, ал жартылай өткізгішті р-типті жартылай өткізгіш деп атайды.

өткізгіш. зона
өткізгіш. зона
Е Е өткізгіш. зона
өткізгіш. зона
.
-----------------------
-----------------------D
EF ----------------------- тиым салын.зона Е F -----------------------
тиым салынған зона
А
валенттік зона
валенттік зона
валенттік зона
валенттік зона
--------------------

О Т

3-сурет 4-сурет

Жартылай - өткізгіштердің өткізгіштігі, заряд тасымалдаушылардың концентрациясымен және қозғалыштығымен (подвижностью) анықталады. Жартылай өткізгіштің температурасын өзгерткенде заряд тасымалдаушылардың қозғалыштығы салыстырмалы аз өзгереді, ал заряд тасымалдаушылардың концентрациясы өте күшті экпоненциалдың заңмен өзгереді. Сол себепті қоспалы жартылай өткізгіштің өткізгіштігі негізінен заряд тасымалдаушылардың концентрациясына байланысты болады. 5-суретте -ның -ға байланысты өзгеру графигі келтірілген.

D меншікті
өткізгіштік

қоспалы
өткізгіштік
C B
A

5-сурет

Бұл графиктің АВ бөлігі қоспалы өткізгіштікті сипаттайды, ал оның температура артқанда артуы, заряд тасымалдаушылардың өткізгіштік зонада концентрациясының артуына байланысты. ВС бөлімі қоспалардағы заряд тасымалдаушылардың қалмағанын көрсетеді. СД-бөлігі жартылай өткізгіштің меншікті өткізгіштігін сипаттайды.

Лекция 11-12
Жартылай өткізгіштің фото өткізгіштігі

Жартылай өткізгіштің фото өткізгіштігі деп жартылай өткізгішке электромагниттік толқын (жарық сәулесі) түскенде оның электр өткізгіштігінің артып кетуін айтады. Бұл құбылыс негізгі материалдың қасиетіне және оған ендірілген қоспаның қасиетіне байланысты болады.
Фото өткізгіштік негізгі материалға байланысты болған кезде жартылай өткізгіш фотон энергиясын жұтуына байланысты болады. Егер жұтылған фотон энергиясы тыйым салынған зонаның энергетикалық мәні Һтең не одан көп болса (1а-сурет) онда электрон валенттік зонадан өткізгіштік зонаға көшіп өтеді, нәтижеде өткізгіштік зонада еркін электрондар, ал валенттік зонада еркін кемтіктер пайда болады. Бұл дегеніміз жартылай өткізгіште меншікті фото өткізгіштік құбылысы пайда болғанын көрсетеді.

а) б) в) өткізгіш зона
өткізгіш зона
өткізгіш зона
валенттік зона
валенттік зона
валенттік зона
өткізгіш зона
өткізгіш зона
өткізгіш зона
валенттік зона
валенттік зона
валенттік зона
1-сурет

Егер жартылай өткізгішке қоспа ендірілген болса, онда фото өткізгіштік болған кезде де пайда болады. Жартылай өткізгішке донорлық қоспа қосылған болса, онда фото өткізгіштік фотон энергиясы болғанда пайда болады (1 б-сурет), ал егер жартылай өткізгішке акценторлық қоспа қосылған болса онда жартылай өткізгіште фото өткізгіштік фотон энергиясы болғанда пайда болады (1 в- сурет). Егер жартылай өткізгіш n-типті болса жарық сәулесінің энергиясын қоспа энергетикалық деңгей жұтатын болса, онда донорлық деңгейден электрондар өткізгіштік зонаға өтеді (1 в- сурет). Жартылай өткізгіш p-типті болса электрондар валенттік зонадан акценторлық энергетикалық деңгейге өтеді (1 в-сурет). Нәтижеде қоспалы фото өткізгіштік құбылысы пайда болады. Осылайша: меншікті жартылай өткізгіш үшін (1), ал қоспалы жартылай өткізгіш үшін (2) болғанда жартылай өткізгіште фото өткізгіштік қозады. Мұнда - қоспа атомдарын қоздыруға керек фотон энергиясының мәні. (1)- теңдеуден фотоөткізгіштіктің қызыл шекарасын анықтау мүмкін.
Фото өткізгіштің қызыл шекарасы деп фото өткізгіштік пайда болатын максимал толқын ұзындықты немесе фото өткізгіштік пайда болатын минимал толқын жиілігін айтады, яғни , ал , онда бұдан меншікті жартылай өткізгіш үшін, ал қоспалы жартылай өткізгіш үшін болады. және - дің мәндерін есепке алсақ, онда меншікті жартылай өткізгіштер үшін фото өткізгіштіктің қызыл шекарасы спектрдің көзге көрінетін толқын ұзындықтарына тура келеді. Ал қоспалы жартылай өткізгіш үшін фото өткізгіштің қызыл шекарасы спектрдің көзге көрінбейтін инфрақызыл толқын ұзындықтарына тура келеді.
Сонымен жартылай өткізгіштің электр кедергісін (өткізгіштігін) жарық сәулесінің түсуімен (жарық толқынының түсуімен) өзгертуін фотоэлектрлік эффект немесе фоторезистивтік эффект деп атайды. Ал фотоэффект құбылысы нәтижесінде қосымша фотоөткізгіштіктің, пайда болуын фотоөткізгіштік деп атайды.
Фотоэффект құбылысы техниканың түрлі салаларында кеңнен қолданылады. Олар фото диодтар, фото кедергілер, фото винтильдер т.б.

Лекция -13,14
Сыртқы электр өрісіндегі жартылай өткізгіш

Түйісу құбылысының негізінде электр өрісінде, жартылай өткізгіште болатын физикалық процесстер жатыр. Бұл құбылысты түсіну үшін жартылай өткізгіштің сыртқы электр өрісінде болғанда пайда болатын қасиеттерін білу керек. Осы мақсатта біртекті электр өрісінде орналасқан электронды жартылай өткізгішті қарастырайық. (1-сурет). Жартылай өткізгіште электр өрісі болмаған кезде көлемдік заряд нөлге тең, ал электр өрісі болған кезде жартылай өткізгіште заряд тасымалдаушылар екіге ажыралады, нәтижеде онда көлемдік заряд пайда болады. Көлемдік заряд, тығыздығы ал электр өрісінің тығыздығы Е(r), болады. Заряд тасымалдаушылардың таралуы көлемдік зарядқа байланысты болады да, зарядтың таралуы жартылай өткізгіштің сыртқы бетінде өзгереді. Көлемдік заряд сыртқы электр өрісін жартылай өткізгіштің ішіне енуіне кедергі жасайды. Сол себепті сыртқы өріс жартылай өткізгіштің сыртқы бетіне әсер етеді.

+ -

1-сурет

Сыртқы электр өрісі 1-суретте көрсетілгендей қосылатын болса, онда жартылай өткізгіштің сыртқы бетінде электрондардың концентрациясы жоғары болады (2 а-сурет) және теріс көлемдік заряз пайда болады (2 б-сурет). Электрондардың артық концентрациясы, яғни көлемдік заряд сыртқы беттен ішке қарай ара-қашықтықты арттыратын болсақ кемиді. Теріс көлемдік заряд Е электр өрісін туғызады. Оның мәні сыртқы бетте максимал болады. (2 в-сурет). Бұл электр өрісі электрондардың потенциал энергиясын өзгертеді (2 г-сурет). Оның шамасы тең болады U(r)=-e, мұнда түйісу өрісінің электростатикалық потенциалы (2д-сурет).
а) б) в)
n
E
x

n0 Es

х x
д) е) г)
U
E Ec
------------------------------ F
x
Ev

x
2-сурет Us

n E

n0 х

x x Es

а) б) в)

U Е
Ес
Us x
---------------------F

x
г) д) е)

3- сурет

Нәтижеде электр өрісі зонаның төменге қарай иілуіне алып келеді (2е-сурет).
, (1)
Бұл кезде барлық энергетикалық деңгейлер иіледі, сонымен бірге қоспаның энергетикалық деңгейде иіледі.
Жартылай өткізгіш термодинамикалық тепе-теңдікте болуына байланысты, Ферми деңгейі тұрақты болады (2е-сурет). Сол себепті Ферми деңгейімен, рұқсат етілген зона арасындағы ара-қашықтық өзгереді. Бұл арақашықтық электр өрісі болмағанда тең болады:
және (2), ал электр өрісі болған кезде және (3).
Егер (2) және (3) теңдеулерді салыстыратын болсақ Ес және F арасындағы арақашықтық U(r)- кемитін болса, онда F және арасындағы арақашықтық дәл осындай шамаға артады.
Ал қойылған өрістің бағытын өзгертетін болсақ электронды жартылай өткізгіштің сыртқы бетіндегі электрондардың концентрациясы кем болады, ал кемтіктердің концентрациясы көп болады, жартылай өткізгіштің көлеміне салыстырғанда (3а-сурет). Ал көлемдік заряд (3б-сурет) және потенциал энергияның өзгерісі (3 г-сурет) таңбасы бойынша оң болады. Бұл жағдайда 3е - суретте көрсетілгендей сыртқы қабатында заряд тасымалдаушылардың таңбасы өзгереді, яғни электронды жартылай өткізгіш, кемтікті жартылай өткізгішке айналады. Бұндай жартылай өткізгіште сыртқы қабаттан белгілі бір қашықтықта өздік электр өткізгіштік қабат пайда болады, яғни і-қабат болады
(3 е-сурет) онда Ферми деңгейі тыйым салынған зонаның ортасында жатады. Бірақ бұл қабат жойылады егер электр өрісін алып тастайтын болсақ. Сонымен жартылай өткізгішті электр өрісіне ендіретін болсақ жартылай өткізгіштің сыртқы қабатында зоналардың энергиялық деңгейі иіледі және электрондар мен кемтіктердің концентрациясы өзгереді. Егер болса зона жоғары қарай иіледі және кемтіктердің концентрациясы артады (3е-сурет). Бұл жағдайда n-типті жартылай өткізгіштің сыртқы бетінде негізгі болмаған заряд тасымалдаушылармен қанығады, ал р-типті жартылай өткізгіштің сыртқы беті негізгі заряд тасымалдаушылармен қанығады.

Лекция 15-16
Шығу жұмысы

Электронды қатты денеден ажыратып шығару үшін энергия жұмсау керек. Бұл дегеніміз қатты дененің сыртқы бетінен электрон ажыралып шығу үшін энергетикалық барьер (тосын) бар дегенді білдіреді. Сол себепті электрон қатты денеден ажыралып шығу үшін осы барьерді (тосынды) жеңуі керек. Ол үшін электронның энергиясы осы барьер энергиясына тең немесе одан үлкен болуы керек. Барьердің кедергісін жеңіп шығатын электрондардың саны артады, егер қатты дененің температурасы артатын болса. Электрондардың заттардан ажыралып шығуы жылулық энергиясы есебінен болатын болса, бұндай құбылысты термоэлектрондық эмиссия құбылысы деп атайды.
Қоздырылмаған жартылай өткізгіштен термоэлектрондық эмиссия құбылысы есебінен пайда болған токтың тығыздығын анықтайық. Ол үшін жартылай өткізгіштен потенциал барьерді жеңіп шығатын электрондардың санын білу керек. Мысалы жартылай өткізгіштен вакуумға ажыралып шыққан электрон энергиясын Еа=Евум деп қабылдайық. Онда электронды өткізгіштік зонаның ең төменгі деңгейінен вакуумға шығару үшін керек энергия тең болады (1-сурет). =Ea-Ec (1), мұнда -өткізгіштік ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.