Сызықты емес теңдеулер жүйесін шешудің сандық әдістері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 102 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

ТҮРКІСТАН ОБЛЫСЫНЫҢ АДАМИ ӘЛЕУЕТТІ ДАМЫТУ БАСҚАРМАСЫ

Ғ. МҰРАТБАЕВ АТЫНДАҒЫ ЖЕТІСАЙ ГУМАНИТАРЛЫҚ-ТЕХНИКАЛЫҚ КОЛЛЕДЖІ

«Математика және физика » кафедрасы

«САНДЫҚ ӘДІСТЕР»

ӘДІСТЕМЕЛІК ЖИНАҚ

Дайындаған: Ұ. Т. Жакупова

Жетісай - 2020

Әдістемелік құрал

Ғ. Мұратбаев атындағы Жетісай гуманитарлық - техникалық колледжінің «Математика және физика » кафедрасында талқыланып, оқу - әдістемелік кеңесінде бекітілді.

№ хаттама

«___» 2020ж

Пікір жазған:

Ғ. Мұратбаев атындағы Жетісай гуманитарлық - техникалық колледжінің директоры педагогика ғылымының кандидаты: Баймаханова Л. А.

Дайындаған:

«Математика және физика » кафедрасының оқытушысы: Жакупова Ұ. Т.

Әдістемелік құрал орта кәсіптік білім беретін оқу орындарының жас мамандары мен студенттеріне арналған.

Алғы сөз

Студентті болашақ мамандығына даярлаудың негізгі міндеттерінің бірі - ұстаз еңбегінің алуан түрлі әрекетінің негізін құраушы практикалық білік пен дағдыларын қалыптастырумен байланысты.

Курстың мақсаты:

«Сандық әдістер» курсының мақсаты -қолданбалы есептерді шешудің жуықтау әдістері, математикалық модельдеу әдістері, кате көздері және нәтиже дәлдігінің әдістері жайындағы түсінікті студенттерге жүйелеңдірілген түрде қалыптастыру. Сондай-ақ таным үрдісінде пайда болатын математикалық есептерді ЭЕМ-ның көмегімең шешудің есептеу алгоритмдерін кұрып, қолдана білуге дайындау. Сонымең қатар, оны практикалық іс-әрекетінде математикалық модельдеудің көмегімен шынайы әлемнің заңдылықтарын пайдалана білу.

ІІәнді оқытудың міндеттері:

- Математикалық моделдеу рөлі және қолданбалы есептерді шешу барысындағы есептеу

Тәжірибесі жайындағы түсініктерін қалыптастыру;

есепті сандық шешу және зерттеу үшін математика пәні бойынша теориялық білімдерін қолдануды студенттерге үйрету;

- қолданбалы есептерді ЭЕМ-ны пайдаланып жуықтап шешу үшін сандық әдістерді пайдалана білу іскерлігін қалыптастыру:

- студенттерді қойылған есепті шешу барысында сандық шешудің тиімді тәмілдерін таңдауға, әр түрлі үрдістермен алынған есептің нәтижелерін салыстыруға үйрету;

- алынған сандық шешімдердің дұрыстағын және дәлдігін тексеру әдісі жайындағы болжамды, жинақтылықты және сандық шешімнің нақты алгоритмдерін қолданудағы қисындылықты негіздеу үшін шешімді алу жылдамдығын тексеру тәсілдерін қалыптастыру;

- есептеу алгоритмдерін математикалық пакәдебиеттер ортасында, не әмбебап программалаудың тілдерінің көмегімен орындай білу іскерлігін қалыптастыру.

Аталған пәнді ойдағыдай меңгеру үшін жоғары математиканың, информатиканың келесі бөлімдерінің базалық білімдерін меңгеру қажет:

- алгебра;

- математикалық таңдау:

- диффереңциалдық теңдеулер;

- ақпараттық технологиялар;

- программалау.

Шеттетілмейтін қателіктер - есептің бастапқы берілгендерінен, коэффициенттерінен, шарттарынан тәуелді қателіктер.

Тура тәсіл - есепті математикалық дәлелденген бір формулаға қою арқылы тікелей шығару.

Итерациялық тәсіл - есепті формула көмегімен бастапқы жуықтауды беру арқылы жуықтап, біртіндеп шығару

Сандық квадратура. Сандық интегралдауды сандық квадратура деп те атайды. Ал қолданылатын формулалар квадратуралық формулалар деп аталады.

Функция класы. К={g(x) }, мұндағы x - тәуелсіз айнымалы немесе бірнеше тәуелсіз айнымалылар жиыны х=(х ₁ , х ₂ , …, х _n ) әлдебір функция класы немесе жиыны берілсін. I=I[g(x) ] айнымалы шамасы g(x) функциясынан функционал (функциядан функция) деп айтады, егер әрбір g(x) ∈K функциясы үшін берілген ереже немесе заң бойынша I анықталған сан сәйкес қойылса.

Функционалдың анықталу облысы. Берілген функционал анықталған К={g(x) }

функциялар класы функционалдың анықталу облысы немесе функционалдың берілу облысы

деп аталады, ал функциялардың өздері мүмкін функциялар деп аталады.

Абсолют қателігі. Әдетте, 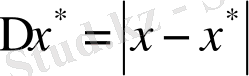шамасын х ^* жуық санының абсолют қателігі деп атйды. Қарасытырыл отырған санның х дәл мәні көбінесе белгісіз болады. Сондықтан 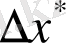қателігі анықтала бермейді. Бірақ оны жоғарыдан шектейтін шаманы әруақытта көрсетуге болады.

Шектік абсолют қателігі . Есептеу математикасында 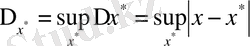шамасын х ^* жуық санының шектік абсолют қателігі деп атайды. Бұл анықтамадан 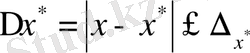екені анық. Демек, 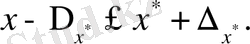Кейде мұны қысқаша 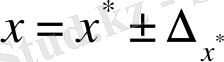деп те жазады.

Салыстырмалы қателігі. 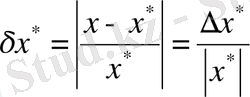шамасын х ^* жуық санының салыстырмалы қателігі деп атайды.

Трапеция әдісі. Егер n=1 болса квадратуралық формула трапеция әдісі деп аталады. Әдіс бойынша; интегралдық қисық пен ох өсі аралығындағы фигура ауданын табу үшін сол фигураны трапециямен толықтырып, ауданын табуға болады:

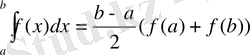
Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады.

Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы функцялары бар теңдеуді айтады.

Студенттерге нақты әдістемелік көмек көрсету мақсатында жазылған

бұл оқу құралы үш тараудан тұрады.
Бірінші тарауында дәрістердің қысқаша конспектісі. Екінші тарауында зертханалық жұмыстарды жүргізуге арналға әдістемелік нұсқаулар. Үшінші тарауында материалды меңгергендігін бағалауға арналған сұрақтар .

Оқу-әдістемелік құрал студенттердің сабаққа дайындалу мен оны
жоспарлау мәселесіне үлкен мән беріп, өзінің педагогикалық еңбегін ғылыми
негізде ұйымдастыруына біршама жеңілдік келтіреді деген сенімдеміз.

Сондайақ, оқу-әдістемелік құралдың қойылып отырған мәселеге қатысты өзіндік тың ойлармен, дәстүрлі емес көзқарастармен ерекшеленетіндігін ескерте кетуге тиіспіз.

Елінің ері емес, езіне айналады. Қазіргі заман - оң құбылыс заманы. Өзгеріс заманы. Ал сіз, келешек заман ұстазысың. Лайықты ел азаматына айналам десең

Сен де бір кірпіш дүниеге,

Кетігін тап та бар қалан, -

деген Абай атаңның сөзін Темірқазыққа санап, іске кіріс.

Сәт сапар, болашақ ұстаздары!

Педагогика ғылымының кандидаты: Баймаханова Л. А.

Мазмұны:

Алғы сөз . . 3

I тарау. Дәрістердің қысқаша конспектісі 5

ІІ тарау. Зертханалық жұмыстарды жүргізуге

арналған әдістемелік нұсқаулар …… . . . . . 66

ІІI тарау. Материалды меңгергендігін бағалауға арналған сұрақтар …. . 113

Қорытынды 114
Пайдаланылған әдебиет тізімі 115

ДӘРІСТЕРДІҢ ҚЫСҚАША КОНСПЕКТІСІ

1-Дәріс тақырыбы: Кіріспе.

Қолданбалы есептердің сандық шешімдерін табу кезеңдері.
Математикалық модель және есептеу эксперименті.
Есептеу математикасы. Сандық әдістерге қойылатын талаптар.
Сандық шешімдерді табу үрдісі кезіндегі қателіктер көзі.
Тиімді әдістер.
Аппроксимациялаулар (жуықтаулар)

Дәріс тезисі:

ХХ ғасырдың орта шенінде атом энергиясын игерудің күрделі жұмыстарына байланысты алғашқы электрондық машиналардың пайда болуы және оларды ары қарай жетілдіру ғылым мен техника саласында революциялық өзгерістер жасады. Ғылымда зерттеу жұмыстарының әдістері күрт өзгеріп, күрделі құбылыстарды зерттеу мен болжау мүмкіндіктері жаңа деңгейге көтерілді. Соның нәтижесінде ғасырлар бойы шешілмей келген ірі ғылыми-техникалық проблемалар өз шешулерін тапты. Ғарышта, атом энергиясын игерудегі жетістіктер электроника мен информатика саласындағы табыстармен тікелей байланысты. Бүгінгі есептеу техникасы күнделікті от басындағы тіршіліктен бастап ғарыштағы күрделі техникалық жүйелерді басқаруға дейін қолданылып жүр. Осы саладағы қол жеткен жетістіктер, бір жағынан математика ғылымының жедел дамуына байланысты болса, екінші жағынана, электрондық есептеуіш машиналар (ЭЕМ) математиканың дамуына өз әсерін тигізді. Мұның бір дәлелі - ЭЕМ-дер математикалық алгоритмдермен және бағдарламалармен жабдықталған.

Электрондық машиналар арқылы есептеу және ойлау жылдамдығы бірнеше миллион есе артып, ғылым мен техниканың күрделі есептерінің математикалық модельдерін жасауға мүмкіндік туды.

Тәжірибелік зор мәні бар есептерді электрондық есептеуіш машиналар арқылы шешу бірнеше сатыдан тұрады:

Бірінші саты - қарастырылып отырған құбылысты (процесті) сипаттайтын көп параметрлердің ішенен ең негізгілерін бөліп алып, оларды байланыстыратын заңдылықтарды пайдалану арқылы физикалық модельдер жасау.

Екінші саты - физикалық модельдерге сәйкес математикалық модельдер құру. Жоғарыда айтылған параметрлер арасындағы сандық қатынастарды математикалық формулалар арқылы жазу. Бұл қатыстар алгебралық, дифференцилдық немесе интегралдық теңдеулер арқылы берілуі мүмкін. Бұл күнде математика және электрондық есептеуіш машиналарын осындай модельдер негізінде пайдалану ғылымның химия, экономика, геология, биология сияқты салаларында кең өріс алып отыр. Математикалық модельдердің үлкен бір ерекшелігі - бір модельмен бірнеше құбылыстар сипатталуы мүмкін.

Үшінші саты - математикалық модельдердің дұрыс құрылғанына көз жеткізу. Мысалы, теңдеулердің шешімдерін табуға болатынын және оның физикалық мағынасы бар екендігін дәлделдеу.

Төртінші саты - математикалық модельдерді сипаттайтын теңдеулерді немесе басқа математикалық есептерді сандық шешудің дұрыс және тиімді әдістерін табу және оның алгоритмін құру.

Бесінші саты - алгоритмдердің бағдарламасын құрып, оны ЭЕМ арқылы есептеу.

Көп жағдайда есептерді математикалық әдістер арқылы ЭЕМ-де дәл шешу мүмкін болмайды. Себебі, біріншіден, ЭЕМ-ді пайдаланар алдында математикалық есептер шекті өлшемге келтіріледі. Шекті өлшемге келтіру, әдетте берілген есепті дискреттеу арқылы орындалады. Бұл жағдайда функцияның үзіліссіз аргументтері дискретті аргументтермен алмастырылады. Есеп дискреттелгеннен кейін оның есептеу алгоритмі құрылып, керекті математикалық және логикалық амалдардың ЭЕМ арқылы қай тәртіпте орындалатыны көрсетіледі.

Ғылым мен техникада көптеген есептер функциялар, алгебралық, дифференциалдық немесе интегралдық теңдеулер арқылы математика тілінде сипатталып жазылады. Мұндай есептер түрліше жолдармен шешіледі. Анализдік әдістер сондай жолдардың бірі болып табылады. Бірақ оларды пайдалану көп жағдайда мүмкін бола бермейді.

Кейінгі 30-40 жыл ішінде жылдам есептейтін электрондық есептеуіш машиналар кеңінен қолданылып келеді. Олардың кейбіреулері секундына жүздеген миллионға дейін арифметикалық амалдар орындайды. Сонымен бірге машиналарда есептеулерді жеңілдететін басқа да қосымша мүмкіншіліктер бар. Электрондық есептеуіш машиналардың пайда болуы есептеу математикасының қарқынды дамуына зор әсерін тигізді.

Есептеу кезінде анализдік әдістерді пайдалану қиындық келтірген немесе тіпті пайдалану мүмкін болмаған жағдайда есептеу математикасының сандық әдістері қолданылады. Ол әдістер бастапқы берілген есепті мағынасы бойынша соған жуық басқа есеппен алмастыру мүмкіндігіне негізделген. Ал соңғы есеп кейбір шарттарды қанағаттандыруы тиіс. Мәселен шешімнің бар болуы, орнықты, жинақты болуы және т. с. с. бұл есептің шешімі алғашқы есептің жуық шешімін беруі тиіс немесе оған белгілі бір дәлдікпен жинақталуы қажет.

Дәл және жуық шешімдердің айырымын жуықтау немесе әдіс қателігі деп атайды.

Есепте негізгі деректер, яғни ондағы коэффициенттер, бос мүшелер немесе қосымша шарттар жуық шамалармен берілуі мүмкін, соның нәтижесінде пайда болған қателіктерді жөнделмейтін (түзетілмейтін) қателіктер деп атайды.

ЭЕМ-де цифрлар саны шексіз көп сандармен арифметикалық амалдар қолданылмайды. Сондықтан ондай сандар ең алдымен цифрларының саны шектеулі жуық сандармен алмастырылады. Ол, әдетте, орта мектептен белгілі дөңгелектеу әдісі арқылы жүзеге асырылады. ЭЕМ-де дөңгелектеу амалы арифметикалық амалдар орындалған кездерде де жүргізіледі. Өйткені нәтижеде цифрларының саны шексіз көп сандар пайда болуы мүмкін. Осындай дөңгелектеулердің салдарынан пайда болған қателіктерді есептік қателіктер деп атайды. Олар есептің жуық шешімінің дәлдігіне тікелей әсерін тигізетіні анық.

Шамалардың жуық мәндері жуық сандармен беріледі. Сандық әдістер немесе есептеу әдістері пәндерінде алынған нәтижелердің барлығы жуық шешімдер деп аталады. Тура шешім мен жуық шешім айырмасы әдіс қателігі немесе дөңгелектеу қателігі деп аталады. Қателіктер 3 түрге бөлінеді:

Әдіс қателігі
Шеттетілмейтін қателік
Есептеу қателігі

Әдіс қателігі берілген есепті шешу үшін таңдалған сандық әдістен тәуелді болады. Осыған байланысты әр әдістің қателігін бағалау формуласы әр түрлі болады. Шеттетілмейтін қателіктер - есептің бастапқы берілгендерінен, коэффициенттерінен, шарттарынан тәуелді қателіктер. Есептеу қателігі жуық шешімдерді алу барысында қолданылатын математикалық есептеулер кезінде қолданылатын сандарды дөңгелектеуден тәуелді.

Қателіктер теориясындағы негізгі ұғымдар

Бұл қателіктердің өздері абсолютті және салыстырмалы ([3] қараңыз) болады.

Егер а саны - тура мән, а*саны оған белгілі жуықтау болса, онда жуықтаудың абсолютті қателігі деп- олардың айырымын, ал шектік абсолютті қателігі деп мына шартты қанағаттандыратын қателікті айтады:.
Жуықтаудың салыстырмалы қателігі деп келесі шартты қанағаттандыратын шартты айтады:немесе

6

Санның мәнді цифрлары деп оның жазылуындағы солдан бастағанда нөлден өзгеше барлық цифрларын айтады.
Мәнді цифрды дұрыс дейді, егер санның абсолютті қателігі осы цифрге сәйкес разряд бірлігінің жартысынан аспаса.

Арифметикалық операциялар нәтижелерінің қателіктері

Қосынды қателігі. F(x) =x=x1+x2+x3+…+xnқосындысы берілсін.

a) қосындының абсолютті қателігі: .

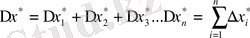Егер 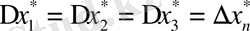болса, онда 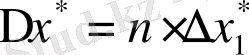, ал n>=10 болса, Чеботарев формуласы қолданылады: .

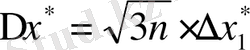b) қосындының салыстырмалы қателігі:

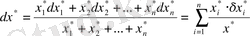. Мұндағы , , .

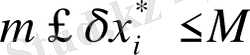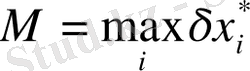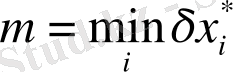2 Айырма қателіктері. X=x ₁ -x ₂ , x ₁ >x ₂ >0 болсын және азайғыш пен азайтқыштың жуық мәндері мен абсолютті қателіктері белгілі болсын.

a) айырманың абсолютті қателігі: .

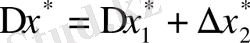b) айырманың салыстырмалы қателігі:

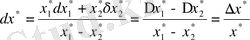3 Көбейтіндінің қателіктері. X=x ₁ *x ₂ *…*x _n көбейтіндісі берілсін. Көбейткіштердің жуық мәндері және абсолютті, салыстырмалы қателіктері белгілі болсын.

a) көбейтіндінің абсолютті қателігі: .

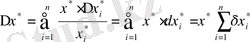b) көбетіндінің салыстырмалы қателігі: .

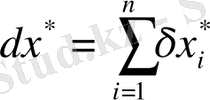4 Бөліндінің қателігі: 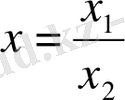бөліндісі берілсін. Алымы мен бөлімінің жуық мәндері, абсолютті, салыстырмалы қателіктері берілген болсын.

a) бөліндінің абсолютті қателігі: .

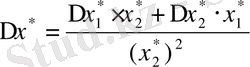b) бөліндінің салыстырмалы қателігі: .

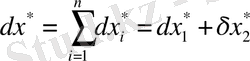1- мысал: Берілген х санының дұрыс цифрлар санын анықтау керек болсын.

; .

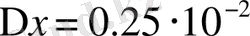Анықтама бойынша: 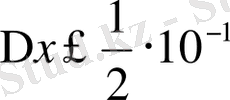шарты орындалса, 3 цифрын дұрыс цифр деуге болады. Шындығында 0, 0025<0, 05 екен, яғни 3 - дұрыс цифр. 9 цифрын тексерсек: 0, 0025<0, 005, яғни 9 цифры да дұрыс. Ал 4 пен 1 цифрлары үшін 0, 0025<0, 0005 және 0, 0025<0, 5

болғандықтан, олар күмәнді цифрлар болады. Қорыта айтқанда үтірден кейінгі 3 және 9 цифрларын жоғалтпау керек, яғни санды 0, 39 деп дөңгелектеуге болады, 0, 4 деп дөңгелектесек дөңгелектеу қателігі өсіп кетеді. Санның дұрыс цифрлар саны төртеу.

2-мысал: 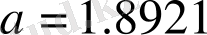; 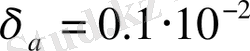берілген. Санның дұрыс цифрларын анықтау.

Анықтама бойынша: 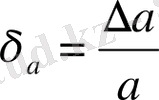, яғни 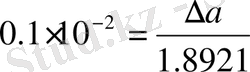. Одан шығатыны: 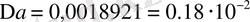. Енді санның цифрларын тексереміз:

8 цифры - дұрыс, өйткені: .

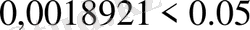9 цифры - күмәнді, өйткені: 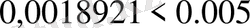. Дәл осылай 2 және 1 цифрларының да күмәнді екенін анықтауға болады. Сонда а санының 2 цифры дұрыс.

3-мысал: Х=2, 1514 санын 3 мәнді цифрға дейін дөңгелектеп, абсолютті және салыстырмалы қателіктерін табу.

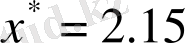болады. Сонда , .

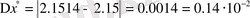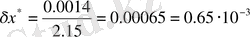4-мысал: 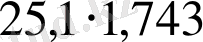көбейтіндісінің абсолютті және салыстырмалы қателіктерін анықтау.

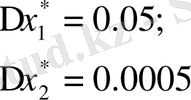екені белгілі. .

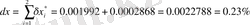2-ДӘРІС ТАҚЫРЫБЫ: Бейсызықты бір теңдеудің түбірін табу.

Түбірлерді бөлектеу. (аралықты екіге бөлу) әдісі.
Жай итерация әдісі.
Ньютон (жанамалар) әдісі.

Дәріс тезисі:

Сандық әдістердің бір бөлімі «бір өлшемді сызықты емес теңдеулер» болып табылады. Физикалық және басқа да құбылыстардың теңдеумен сипатталатыны белгілі. Сол теңдеуді классикалық математикалық формуламен шешу мүмкін емес жағдайлар бар. Бұл уақытта практикада сандық әдістерге жататын әдістермен шешілетінін дәлелдеу керек. Әрине ең алдымен құрылған теңдеудің қай аралықта анықталғандығын, үзіліссіздігін, түбірінің барлығын, оның жалғыздығын дәлелдейтін аргументтерді бақылау керек. Осы этаптан өткеннен кейін ғана есепті осы теңдеуге қолдануға келетін алгоритм көмегімен шығаруға болады.

Сызықты емес теңдеулер екі түрлі:

алгебралық
трансцендентті.

Алгебралық теңдеулер деп алгебралық көпмүшеліктерден тұратын теңдеулерді айтады. Олардың шешімдері көбіне нақты сан болады.

Трансцендентті теңдеу деп құрамында тригонометриялық немесе арнаулы функцялары бар теңдеуді айтады.

Сызықты емес теңдеуді сандық шешу екі тәсілден ([1] қараңыз) тұрады.

1. Тура тәсіл - есепті математикалық дәлелденген бір формулаға қою арқылы тікелей шығару.

2. Итерациялық тәсіл - есепті формула көмегімен бастапқы жуықтауды беру арқылы жуықтап, біртіндеп шығару.

Тура тәсілмен шығарылған есептер дәл мәнді береді. Ал итерациялық тәсілмен шешілген есептер есептің жуық мәнін береді . Мұның ішінде итерациялық әдістер сандық әдіске жатады.

Бір өлшемді сызықты емес теңдеуді шешудің келесі әдістері бар.

1. Кесіндіні қақ бөлу - дихотомия әдісі деп аталады.

2. Хорда әдісі.

3. Жанама әдісі немесе Ньютон әдісі

4. Қарапайым итерациялық әдіс немесе жәй итерация әдісі т. б.

Түбір жатқан аралықты анықтау әдісі

F(x) =0 (1. 1)

Бірөлшемді сызықты емес теңдеу берілген. Мұндағы F(x) функциясы [a, b] кесіндісінде анықталған және үзіліссіз болсын.

Теорема1. 1: [а, в] аралығында анықталған, үзіліссіз F(x) функциясының екі шеткі нүктелердегі мәндерінің таңбалары әр түрлі болса, яғни мына шарт орындалса f(a) *f(b) <0, онда осы аралықта (1. 1) -теңдеудің түбірі бар және жалғыз болады.

Практикада кейде теореманың орындалуын функцияның мәндер кестесін құру арқылы да анықтайды. Функцияның анықталу облысы бойынша а нүктесін беріп, ол нүктедегі функция мәнін анықтайды, сосын һ қадаммен келесі нүктеге жылжып, сол нүктедегі функция мәнін анықтайды, сол сияқты бірнеше нүктедегі функция мәндерін анықтап, таңбасын салыстырады. Егер көрші нүктелерде функция әр түрлі таңба қабылдаса, сол аралықта жалғыз түбірі жатыр деп айтады.

Кесіндіні қақ бөлу әдісі

(1. 1) - теңдеуді кесіндіні қақ бөлу әдісімен шешу алгаритмі келесі қадамнан тұрады.

(1. 1) -ші теңдеудің түбірі жатқан аралығын анықтау және осы аралықта түбірдің жалғыздығын тексеру. Яғни x осі бойында бірдей қашықтықта жатқан нүктелердегі функцияның мәндерін есептеміз, және егер екі шеткі нүктеде немесе екі көрші нүктеде функция мәндерінің таңбалары әр түрлі болса, онда сол аралықта түбір бар деп есептеу
Осы аралықты қаққа бөлу және ол нүктенің мәнін

X _орт =(X _n+1 +X _n ) \2. (1. 2)

формуласымен анықтау.

Xn+1-Xn<e шарты арқылы қарастырылып отырған аралықтан шығып кетпеуді бақылаймыз.
XОРТнүктесіндегі функция мәнін F(XОРТ) есептеу.
Егер оның таңбасы F(Xn) функциясының таңбасымен бірдей болса, Xnнүктесінің орнына XОРТнүктесін қарастырамыз.
Ал егер F(XОРТ) функциясының таңбасы F(Xn+1) функциясының таңбасымен бірдей болса, Xn+1нүктесінің орнына ХОРТнүктесін қарастырамыз.
Шыққан аралықтар [Xn,, Хорт] U [Xорт, Xn+1] белгіленеді. және алдыңғы шарттарға байланысты екі аралықтың біреуін тағы қаққа бөлу арқылы ізделінді нүктеге біртіндеп жақындаймыз. Яғни мына шарттар тексеріледі: F(Xn+1) *F(Xорт) <0 шарты орындалса [Xорт, Xn+1] аралығы қаққа бөлінеді де шыққан нүкте мәні, XОРТ2=XОРТ+ Xn+1/2 формуласымен есептеледі. F(Xn) *F(ХОРТ) <0 шарты орындалса [Xn, Xорт] аралығы қаққа бөлініп, табылған нүкте XОРТ2=XОРТ+ Xn/2 формуласымен есептеледі.
Осы процесті іздеп отырған х нүктесіне жеткенге дейін жалғастырып, XОРТ, XОРТ2, XОРТ3, …, XОРТNтізбегін құрамыз. Мына шарт орындалатын уақытта XОРТN- XОРТN-1<E іздеу процесін тоқтатамыз да XОРТNнүктесін (1. 1) -ші теңдеуді қанағаттандыратын х дәл түбірге жуық мән деп қабылдаймыз.

Жай итерация әдісі

Бұл әдісті қолдану үшін (1. 1) -ші теңдеудің сызықты мүшесі айшықталып мына түрге келтіру керек:

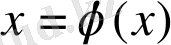(1. 3)

Сосын теңдеудің түбіріне кез келген Х ₀ бастапқы жуықтау беріп 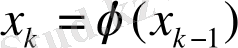k=1, 2, … формуласымен х ₁ , х ₂ , …, х _n нүктелер тізбегін құрамыз. Бұл тізбек x=z түбіріне жинақталуы керек. Егер limX _k =z болса, онда z нүктесі 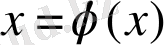теңдеуінің түбірі бола алады. Итерация әдісінің жинақтылық шарты 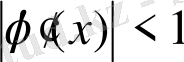және бастапқы жуықтау кез келген болады. Итерациялық процесс берілген дәлдікке жетуі үшін 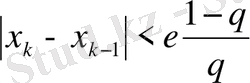шарты орындалуы керек.

Итерациялық тізбектің жинақтылығы теореманың ([1] қараңыз) шарттарымен де тексерілуі керек:

Теорема1. 2. :

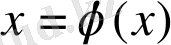теңдеуінің [a, b] аралығында жалғыз түбірі бар және келесі шарттар орындалсын:

1) 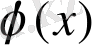функциясы [a, b] аралығында анықталған және дифференциалданады;

2) 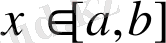үшін ;

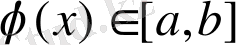3) барлық 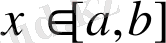үшін 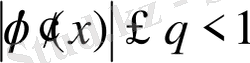болатындай q саны табылсын,

онда 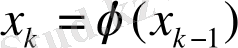, (k=1, 2, …) итерациялық тізбегі 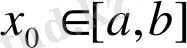кез келген бастапқы жуықтауда жинақталады.

Хорда әдісі

Бұл әдіс кесіндіні қаққа бөлу әдісіне қарағанда шешімге тез жинақталады.

Алгоритмі:

хn, xn+1аралығында f (x) және f (xn+1) функцияларының таңбасы бір біріне қарама-қарсы және түбірі бар болсын.
Осы екі шеткі нүктеден хорда жүргізіп, хорданың х осімен қиылысқан нүктесін мына формуламен анықтаймыз.

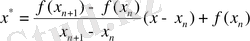(1. 4)