Математиканы оқыту теориясы мен әдістемесі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым министрлігі М.Мәметова атындағы Қызылорда педагогикалық жоғары колледжі
Физика-математика және ақпараттық жүйе бөлімі

Қорғауға жіберілді
ПЦК төрайымы:
___________ Г. Жұмағұлова
_____ ______________ 2023 ж

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Сызықтық функция және оның графигін оқыту әдістемесі
Пәні: Математиканы оқыту теориясы мен әдістемесі
Мамандығы: 0111000- Негізгі орта білім беру
Біліктілігі: 0111113- Ағылшынша білімі бар математика пәні мұғалімі
Тобы: М-Л-19

Орындаған: Алиев Әділет
Ғылыми жетекшісі: Сауяева Нұргүл

Бағасы: _________________

Қызылорда, 2023 жыл
М.Мәметова атындағы Қызылорда педагогикалық жоғары колледжі, 0111000 - Негізгі орта білім беру мамандығының Мл-19 оқу тобының студенті А.Әділеттің сызықтық функция және оның графигі тақырыбындағы курстық жұмысына

ПІКІР

Курстық жұмыс кіріспеден, екі тараудан, тәжірибелік бөлімнен, қорытындыдан тұрады. Кіріспеде жұмыстың мақсаты мен міндеттері, зерттелуі талданады.
Курстық жұмыстың бірінші сызықтық тәуелділік және онымен байланысты теңдеулер мен теңсіздіктердің теориялық негізі бөлімін зерттей алған.
Курстық жұмыстың теориялық бөлімінде сызықтық функция ұғымының әдіснамалық базасы анықталды
Дипломдық жұмыстың жетістіктері: Теориялық бөлімдегі мәліметтерді, тәжірбие жүзінде дұрыс әрі нақты қолдана білген.
Қорытынды: Ә.Алиевтің курстық жұмысы барлық талаптарға сай жазылған. Жұмысты қорытынды аттестациялау комиссиясына қорғауға ұсынып, ______________ деп бағалаймын

Пікір беруші: ... ... ... ... ... ... ... ... ... ... ... ... пән оқытушының аты-жөні,
күні жазылады.
(Мекеме мөрімен)

МАЗМҰНЫ
КІРІСПЕ____________________________ ______________________________4-5
I ТАРАУ. СЫЗЫҚТЫҚ ТӘУЕЛДІЛІК ЖӘНЕ ОНЫМЕН БАЙЛАНЫСТЫ ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІҢ ТЕОРИЯЛЫҚ НЕГІЗІ
1.1 Функция ұғымы және оны анықтаудың әртүрлі әдістері_______________6-11
1.2 Ұғымдарды енгізу әдістемесі: функциялары, аргументі, анықтау саласы_____________________________ _____________________________11-17
1.3 Сызықтық функция ұғымы және оның мәні,графигі__________________17-21
1.4 Сызықтық теңдеулер мен теңсіздіктер_______________________ _________21
II ТАРАУ. СЫЗЫҚТЫҚ ФУНКЦИЯ ЖӘНЕ ОНЫҢ ГРАФИГІНІҢ НЕГІЗІНДЕ МЕКТЕП ОҚУШЫЛАРЫН ОҚЫТУДЫҢ ӘДІСТЕМЕЛІК НЕГІЗДЕРІ
2.1 Функция X және онымен байланысты теңдеулер мен теңсіздіктерді оқыту әдістемесі_________________________ ______________________________22-23
2.2 Сызықтық теңсіздіктерді шешу жолдары__________________________23 -25
2.3 Сызықтық функция үшін кері функция, есептер шығару әдістемесі____25-26
Тәжірибелік бөлім______________________________ __________________27-29
ҚОРЫТЫНДЫ__________________________ ____________________________30
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ_____________________________ ___31

КІРІСПЕ

Зерттеудің өзектілігі: Мектептегі математика курстарындағы басты орынды оқушылардың математикалық қабілеттерін дамытуда тиімді тақырыптар алуы керек. Қарапайым математиканың бұл бөлімдері қазіргі кездегі математика ғылымының жағдайына қатты тәуелді емес. Дәл осы тақырыптардың бірі - "сызықтық функциялар"тақырыбы.
"Сызықтық функциялар" тақырыбын зерттеу бағдарламаға негізгі компонент ретінде енеді, ал қорытынды тестілеу кезінде В және С топтарының тапсырмаларына осы тақырыптағы мысалдар кіреді. Алайда, кері функцияларды зерттеу оқушылар үшін үлкен қиындықтар тудыратындығына күмәнданудың қажеті жоқ. Оқушылар тіпті қарапайым тапсырмаларды шеше алмайды, күрделілігі жоғары мысалдарды айтпағанда, көбінесе оларға бөртпе әрекеттер жасайды, шешімді ресми түрде "стандартқа сәйкес"орындайды. Мұғалім жақсы стратег болуы керек және балалардың ақыл-ойы үшін уақытында қиындықтар тудыруы керек. Бұл қиындық: балалардың білім шыңына жету жолындағы барлық кедергілерді жоя алмау, оларды жүйелі түрде құру, бұл балаларға мектеп бағдарламасын саналы түрде игеруге ғана емес, сонымен бірге олардың жеке басын қалыптастыру жолында тура жылжуға мүмкіндік береді.
Функциялардың мінез-құлқын зерттеу және олардың графиктерін құру математиканың маңызды бөлімі болып табылады. Графикалық техниканы еркін меңгеру көбінесе көптеген мәселелерді шешуге көмектеседі және жұп оларды шешудің жалғыз құралы болып табылады. Сонымен қатар, функциялардың графигін құру мүмкіндігі үлкен тәуелсіз қызығушылық тудырады.
Функция ұғымы адамдар өздерінің айналасындағы құбылыстардың өзара байланысты екенін тураш түсінген кезде пайда болады. Ежелгі Египет, Вавилон, Грециядан бері математиканың дамуы аз жолдан өтіп, өзгеріп, өзгерді.
Нақты әлем процестерін (физикалық, химиялық, биологиялық, экономикалық және басқалардың барлық түрлері) зерттеу кезінде біз оларды сипаттайтын, қарастырылатын процестер барысында өзгеретін шамалармен үнемі кездесіп отырамыз. Бұл ретте жиі өзгерту бір шамасын сопутствует және өзгерту екіншісіне немесе, тіпті, оның үстіне, өзгерту-бір шама болып табылады өзгерту себебі басқа. Қарастырылған шамалардың сандық сипаттамаларының өзара байланысты өзгерістері тиісті математикалық модельдерде олардың функционалды тәуелділігіне әкеледі. Сондықтан функция ұғымы математика мен оны қолданудағы маңызды ұғымдардың бірі болып табылады.
Мектеп курсы талдау принциптеріне қатысты ұғымдарды, тұжырымдар мен әдістерді мазмұнды ашумен, олардың практикалық маңыздылығын анықтаумен сипатталады. Талдау мәселелерін зерттеуде көрнекі ойлар кеңінен қолданылады: презентацияның қатаңдығы деңгейі талдау принциптерін зерттеудің жалпы бағытын ескере отырып анықталады және байланысты пәндерде зерттелетін материалды қолданудың қатаңдық деңгейіне сәйкес келеді
Зерттеу базасы: Ә.Мүсілімов атындағы 101 мектеп-лицейі
Зерттеу нысаны: 5 - 9 сынып оқушылары
Зерттеу пәні: Математиканы оқыту әдістемесі
Зерттеу мақсаты: сызықтық функциялар ұғымдарын қалыптастыру, сонымен қатар математиканы тереңдетіп оқытатын мектептер мен сыныптарда осы тақырыпты оқыту әдістемесін жасау.
Зерттеу міндеттері:
oo функция ұғымы және оны анықтаудың әртүрлі әдістерін талдау;
oo ұғымдарды енгізу әдістемесі: функциялары, аргументі, анықтау саласын айқындау;
oo сызықтық функция ұғымы және оның мәні,графигін анықтау;
oo сызықтық теңдеулер мен теңсіздіктер жүйесін қарау;
oo функция X және онымен байланысты теңдеулер мен теңсіздіктерді оқыту әдістемесін анықтау;
oo сызықтық теңсіздіктерді шешу жолдарын қарастыру;
oo сызықтық функция үшін кері функция, есептер шығару әдістемесін зерттеу;
Зерттеудің әдіс-тәсілдері: Түсіндіру, әңгімелесу, зерттеу, проблемалық, практикалық..
Курстық жұмыстың құрылымы: кіріспе, 3 тарау, қорытынды, пайдаланылған әдебиеттер тізімі. Әр тарау зерттелген материал негізінде жастуран қорытындымен аяқталады. Жұмыс зерттеуге негізделген қорытындымен аяқталады.

I ТАРАУ. СЫЗЫҚТЫҚ ТӘУЕЛДІЛІК ЖӘНЕ ОНЫМЕН БАЙЛАНЫСТЫ ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІҢ ТЕОРИЯЛЫҚ НЕГІЗІ

1.1 Функция ұғымы және оны анықтаудың әртүрлі әдістері

XVII ғасырдан бастап маңызды ұғымдардың бірі-функция ұғымы. Ол осы күнге дейін нақты әлемді білуде үлкен рөл атқарды.
Функционалды тәуелділік идеясы ежелгі дәуірден басталады, ол шамалар арасындағы турашқы математикалық түрде көрсетілген қатынастарда, сандарға қатысты турашқы ережелерде, белгілі бір фигуралардың ауданы мен көлемін табуға арнтуран турашқы формулаларда кездеседі.
4-5 мың жыл бұрын S шеңберінің ауданы үшін радиусы R формуласын тапқан Вавилон ғалымдары S=3r2 (шамамен шамамен), осылайша шеңбердің ауданы оның радиусының функциясы екенін саналы түрде емес, анықтады. Вавилондықтар қолданған квадраттар мен сандардың текшелері-бұл функцияның тапсырмалары.
Алайда, функция ұғымын нақты және саналы түрде қолдану және функционалды тәуелділікті жүйелі түрде зерттеу XVII ғасырда пайда болды.айнымалылар идеясының математикаға енуіне байланысты. Декарттың "геометриясында" және Ферма, Ньютон және Лейбництің еңбектерінде функция ұғымы интуитивті болды және геометриялық немесе механикалық көріністермен байланысты болды: қисық нүктелердің ординаттары - абсцисстен (х); жол және жылдамдық - уақыттан (t) және т.б. функциялар.
XVII ғасырдағы функция ұғымының нақты көрінісі әлі болған жоқ, Декарт турашқы осындай анықтамаға жол ашты, ол өзінің "геометриясында" теңдеулерді, сонымен қатар aлгебралық теңдеулерді қолдана отырып, дәл елестете алатын қисықтарды жүйелі түрде қарастырды. Бірте - бірте функция ұғымы аналитикалық өрнек-формула ұғымымен анықтала бастады.
Осы анықтамалардан көрініп тұрғандай, функция ұғымы іс жүзінде аналитикалық өрнекпен анықталды. XIX ғасырдағы жаратылыстану мен математиканың дамуындағы жаңа қадамдар функция ұғымын одан әрі жалпылауға себеп болды.
Бұл функцияны түсіну керек деген мәселеге француз математигі Жан Батист Джозеф Фурье (1768-1830) негізінен математикалық физикамен айналысқан. Ол 1807 және 1811 жылдары Париж Ғылым Академиясына ұсынған қатты денеде жылудың таралу теориясы бойынша еңбектерде Фурье әртүрлі аналитикалық өрнектермен әр түрлі бөлімдерде берілген функциялардың турашқы мысалдарын келтірді.
Фурье еңбектерінен кез-келген қисық қанша және қандай гетерогенді бөліктерге қарамастан, бірыңғай аналитикалық өрнек түрінде ұсынылуы мүмкін және аналитикалық өрнекте бейнеленген үзік қисықтар да бар екендігі анықталды. 1821 жылы жарық көрген" алгебралық талдау курсында " француз математигі Коши Фурье тұжырымдарын негіздеді. Осылайша, физика мен математиканың белгілі даму кезеңінде анықтау үшін тек аналитикалық аппаратпен шектелу өте қиын немесе тіпті мүмкін емес функцияларды қолдану керек екені белгілі болды.
1834 жылы " жолдардың жоғалуы туралы" еңбегінде Н. И. Лобачевский 1755 жылы жоғарыда аттуран Эйлер функциясының анықтамасын дамыта отырып, былай деп жазды: "жалпы ұғым х функциясынан әр Х үшін берілген және Х-мен бірге берілген санды атауды талап етеді.біртіндеп өзгереді. Функцияның мәнін аналитикалық өрнек немесе құрал барлық сандарды сынап көруге және олардың біреуін таңдауға мүмкіндік беретін шарт бере алады; немесе, сайып келгенде, тәуелділік болуы мүмкін және белгісіз болып қалуы мүмкін... Теорияның кең көзқарасы тәуелділіктің бар болуына тек бір-бірімен байланысты сандарды бір-бірімен бірге деректер ретінде қабылдауға мүмкіндік береді".
Лобачевскийден бұрын да функция тұжырымдамасына ұқсас көзқарасты чех математигі Б. Больцано айтқан. 1837 жылы неміс математигі П. Лежен-Дирихле функция ұғымының жалпы анықтамасын тұжырымдады:"х айнымалысының функциясы бар (A Pound x Pound b кесіндісінде), Егер х - ның әр мәні (осы кесіндіде) нақты анықттуран мәнге сәйкес келсе және бұл сәйкестік қалай анықттуранына бей-жай қарамайды-аналитикалық формула, график, кесте немесе тіпті жай сөздер".
Осылайша, XIX ғасырдың ортасында. пікірлердің ұзақ күресінен кейін функция ұғымы аналитикалық өрнектің байланысынан, математикалық формуланың автократиясынан босатылды. Функция ұғымының жаңа жалпы анықтамасындағы басты назар сәйкестік идеясына аударылады.
XIX ғасырдың екінші жартысында. жиын теориясын құрғаннан кейін функция ұғымына сәйкестік идеясынан басқа жиын идеясы да енгізілді. Осылайша, толық көлемде функция ұғымының жалпы анықтамасы келесідей тұжырымдалады: Егер А жиынының әр элементі В жиынының белгілі бір элементіне сәйкес келсе, онда А жиынында у = f (X) функциясы берілген немесе А жиыны в жиынында көрсетілген деп айтылады. бірінші жағдайда А жиынының элементтері аргумент мәндері деп аталады, ал В жиынының элементтері функцияның мәндері деп аталады; екінші жағдайда х-прототиптер, у-суреттер. Қазіргі мағынада Дирихле анықтамасында айтылған a Pound x Pound b кесіндісін толтырмайтын x мәндерінің жиынтығы үшін анықттуран функцияларды қарастырыңыз. Мысалы, функцияны көрсету жеткілікті-факториал y = n ! натурал сандар жиынында берілген. Функцияның жалпы тұжырымдамасы, әрине, тек шамалар мен сандарға ғана емес, сонымен қатар басқа математикалық нысандарға, мысалы, геометриялық фигураларға да қолданылады. Кез-келген геометриялық түрлендіруде (дисплейде) біз функциямен айналысамыз.
Дирихле функциясының жалпы анықтамасы XVIII және XIX ғасырдың бірінші жартысындағы физика мен математикадағы маңызды ашылулардың нәтижесінде ғасырлар бойы созылған пікірталастардан кейін пайда болды. Бірақ ХХ ғасырдың басынан бастап.бұл анықтама математиктердің бір бөлігі арасында күмән тудырды. Функцияға кеңірек қарауды қажет ететін құбылыстарға тап болған физиктердің сыны одан да маңызды болды. Функция ұғымын одан әрі кеңейту қажеттілігі 1930 жылы Кванттық механиканың негізін қалаушылардың бірі, ірі ағылшын физигі Пол Дирактың "кванттық механиканың негіздері" кітабы жарық көргеннен кейін өткір болды. Дирак дельта деп аталатын функцияны енгізді, ол функцияның классикалық анықтамасынан асып түседі. Осыған байланысты кеңестік математик Н. М.Гюнтер және басқа ғалымдар біздің ғасырдың 30-40-шы жылдары нүкте функциялары емес, құбылыстардың физикалық мәніне сәйкес келетін "аймақ функциялары" белгісіз жұмыстарды жариялады.
Жалпы туранда, жалпыланған функция ұғымын француз Лоран Шварц енгізген. 1936 жылы 28 жастағы кеңестік математик және механик Сергей Львович Соболев алдымен дельта функциясын қамтитын жалпыланған функцияның ерекше жағдайын қарастырды және құрылған теорияны Математикалық физиканың бірқатар мәселелерін шешуге қолданды. Жалпыланған функциялар теориясының дамуына Л.Шварцтың шәкірттері мен ізбасарлары - И. М. Гельфанд, Г. Е. Шилов және басқалар маңызды үлес қосты.
Функция ұғымының дамуының тарихи жолын бақылай отырып, сіз эволюция әлі аяқттуран жоқ және ешқашан аяқталмайды деген ойға еріксіз келесіз, өйткені математика эволюциясы толығымен аяқталмайды. Жаратылыстану және басқа ғылымдардың жаңа ашылымдары мен сұраулары функция ұғымының және басқа математикалық ұғымдардың жаңа кеңеюіне әкеледі. Математика - бұл аяқталмаған ғылым, ол мыңдаған жылдар бойы дамыды, біздің дәуірімізде дамып, болашақта дамиды.
Мектептегі математика курсының жетекшісі ретінде функционалды сызықты негіздеу қазіргі техниканың ең үлкен жетістіктерінің бірі болып табылады. Алайда, бұл ережені жүзеге асыру көптеген жолдармен жүзеге асырылуы мүмкін; жолдардың әртүрлілігі функция ұғымының өзіндік негізімен байланысты.
Осы әртүрлілік туралы түсінік қалыптастыру үшін біз осы тұжырымдаманың ең күрт ерекшеленетін екі әдістемелік түсіндірмесін салыстырамыз; біріншісін генетикалық, екіншісін логикалық деп атаймыз.
Функция ұғымының генетикалық түсіндірмесі XIX ғасырдың ортасына дейін функция ұғымына енген негізгі белгілердің дамуына және әдістемелік дамуына негізделген.осы түсіндіруде функционалды идеялар жүйесіне енетін ең маңызды ұғымдар айнымалы, айнымалы шамалардың функционалды тәуелділігі, формула (басқа айнымалылардың кейбір комбинациясы арқылы бір айнымалыны білдіретін), жазықтықтағы декарттық координаттар жүйесі.
Функция ұғымының генетикалық дамуы бірқатар артықшылықтарға ие. Ол функционалдық тәуелділік тұжырымдамасының "динамикалық" сипатын атап көрсетеді, табиғат құбылыстарын зерттеуге қатысты функция тұжырымдамасының модельдік аспектісі оңай анықталады. Мұндай түсіндіру алгебра курсының қтуран мазмұнымен табиғи түрде байланысты, өйткені онда қолданылатын функциялардың көпшілігі аналитикалық немесе кестелік түрде көрінеді.
Функция ұғымының генетикалық түсіндірмесінде шектеу ретінде қарастырылуы керек белгілер де бар. Өте маңызды шектеулердің бірі-бұл тәсілмен айнымалы әрдайым анық емес (немесе тіпті анық) сандық мәндердің үздіксіз қатарынан өтеді деп болжанады. Сондықтан тұжырымдама көбінесе бір сандық Аргументтің сандық функцияларымен ғана байланысты (сандық интервалдарда анықттуран). Тренингте сіз функционалды идеяларды қолдана және дамыта отырып, оның бастапқы сипаттамасынан тыс үнемі шығуыңыз керек.
Функция ұғымын логикалық түсіндіру функционалды идеяларды оқытуды алгебралық жүйе ұғымының шеңберіндегі функция ұғымын әдістемелік талдау негізінде құру керек деген ережеден туындайды. Бұл тәсілдегі Функция функционалдылық жағдайын қанағаттандыратын екі жиын арасындағы ерекше түрдің қатынасы ретінде әрекет етеді. Функция ұғымын зерттеудің бастапқы кезеңі оны қатынас тұжырымдамасынан шығару болып табылады.
Логикалық тәсілді жүзеге асыру функция ұғымын әр түрлі құралдарды қолдана отырып суреттеу қажеттілігін тудырады; мектеп математикасының тілі байытылады. Формулалар мен кестелерден басқа, олар көрсеткілермен функцияны тағайындау, жұптарды санау, тек сандық емес, сонымен қатар геометриялық материалды пайдалану үшін өз орнын табады; осы тәсілмен геометриялық түрлендіруді функция ретінде қарастыруға болады. Пайда болған тұжырымдаманың жалпылануы және математиканы оқытуда әртүрлі байланыстар орнату мүмкіндігі -- бұл түсіндірудің негізгі артықшылықтары.
Алайда, осы жолда дамыған жалпы тұжырымдама негізінен бір сандық аргументтің сандық функцияларымен, яғни генетикалық негізде әлдеқайда оңай қалыптасатын саламен байланысты болады.
Осылайша, егер генетикалық тәсіл жалпыланған ұғым ретінде функцияны қалыптастыру үшін жеткіліксіз болса, онда логикалық белгілі бір резервті анықтайды. Функцияны түсіндірудегі айырмашылықтар осы тұжырымдаманы енгізу кезінде айқын көрінеді. Функционалды сызықты одан әрі зерттеуде айырмашылықтар біртіндеп жойылады, өйткені ол алгебра курстарында зерттеліп, талдау басталды, бұл функция ұғымы емес, негізінен нақты көрсетілген функциялар мен функциялар сыныптары, олардың жаратылыстану және әлеуметтік өндіріс есептеріндегі әртүрлі қосымшалары.
Қазіргі мектептегі математика курсында ұзақ әдістемелік ізденістердің нәтижесінде функция ұғымына генетикалық көзқарас жетекші ретінде қабылданды. Сонымен қатар, логикалық тәсілден алуға болатын барлық құнды заттар ескеріледі. Осыған сүйене отырып, ұғымдар мен идеяларды, әдістер мен әдістерді функционалдық сызықтың бөлігі ретінде қалыптастыру кезінде оқыту жүйесі студенттердің назарын, біріншіден, функциямен байланысты анықттуран және нақты анықттуран идеяларға, екіншіден, олардың өзара әрекеттесуін орнатуға бағыттайтын етіп құрылады.оқу материалын орналастыру кезінде. Басқаша айтқанда, оқытуда функция ұғымының құрамдас бөліктері жүйесі бөлініп, олардың арасындағы байланыс орнатылуы керек. Бұл жүйеге келесі компоненттер кіреді:
- айнымалылардың функционалдық тәуелділігі туралы түсінік
-нақты процестер мен математикадағы шамалар;
- функция туралы түсінік сәйкестік ретінде;
- функция графиктерін құру және пайдалану, функцияларды зерттеу;
- әр түрлі анықттуран функциялардың мәндерін есептеу тәсілдермен.
Алгебраны оқыту процесінде барлық осы компоненттер функция тұжырымдамасына кез-келген тәсілмен қатысады, бірақ олардың біреуіне баса назар аударуға болады. Біз атап өткендей, функционалды компонент-бұл функция ұғымын енгізу мен зерттеудің негізі. Осы негізде анықтамамен жұмысты ұйымдастырған кезде функционалды тәуелділікті және оның графикалық көрінісін анықтаудың әртүрлі тәсілдерінде көрінетін басқа компоненттер енгізіледі.
Енді қолданбалы дағдыларды қалыптастыруға қатысты мысалда компоненттердің өзара әрекеттесуін қарастырыңыз.
Мысал 1. Аяздан олар бөлмеге мұз құмырасын салып, құмырадағы зат температурасының өзгеруін байқай бастады: мұз біртіндеп ериді, ол бүкіл еріген кезде судың температурасы бөлмедегі температураға тең болғанша көтеріле бастады. Суретте температураның уақытқа тәуелділік графигі көрсетілген.

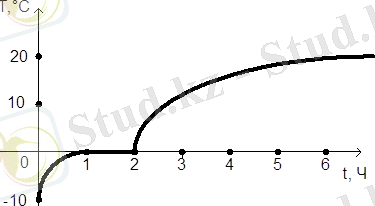
Сұрақтарға жауап беру: а) мұздың бастапқы температурасы қандай? б) мұздың температурасы қай уақытта 0 °С-қа дейін көтерілді? в) бөлмедегі температура қандай? г) функция анықттуран аймақты, оның өсу аралықтарын, ол тұрақты болатын аралықты көрсетіңіз.
Бұл мысалда есептеу компонентінен басқа барлық компоненттерді пайдалану қажет. Басынан бастап Процесс функционалды тәуелділік ретінде ұсынылған. Сұрақтарда осы тәуелділіктің сипатын нақтылау (сұрақ г)), процестің белгілі бір сәттеріндегі функция мен Аргументтің тиісті мәндерін анықтау қажет (сұрақтар А және в).
Функция ұғымы, оның қалыптасу жүйесінде осындай тапсырмалар болуы керек, бірден математика курсында белгілі бір математикалық модель ретінде әрекет етеді, бұл оны терең зерттеуге түрткі болады.

1.2 Ұғымдарды енгізу әдістемесі: функциялары, аргументі, анықтау саласы

Функция тұжырымдамасының өте үлкен көлеміне, кеңдігі мен күрделілігіне қарамастан, оның қарапайым нұсқасы мектептің орта сыныптарында берілген. Бұл ұғым алгебра мен талдау принциптерін зерттеуде негізгі ұғым бола отырып, одан әрі маңызды рөл атқарады. Орта мектептің 7-ші сыныбынан бастап функциялар мен функционалдық тәуелділіктердің қасиеттері біртіндеп зерттелуде. Функциялардың әртүрлі кластары қарастырылады: қарапайым сызықтық функциялар мен олардың графиктерінен бастап, содан кейін квадраттық функциялар, кері пропорционал функциялар және бөлшек-сызықтық функциялар. Жоғары сыныптарда функциялар, соңында экспоненциалды және логарифмдік функциялар енгізіледі. Барлық осы функциялар тек бір айнымалының функциялары ретінде қарастырылады, ал айнымалылардың өзі нақты сандар жиынынан аспайды.
Қазіргі уақытта педагогикалық ізденіс толқынында мектепте қолдануға арнтуран көптеген эксперименттік оқулықтар пайда бола бастады. Жақсы, түсінікті жазылған оқулықтармен қатар, тестілеу сылтауымен мектептерге оқу материалын, оның ішінде функцияларды зерттеуге қатысты тарауларды еркін түсіндіретін көптеген оқулықтар түсе бастады. Зерттелетін бөлімдерді ұстанудың логикалық тәртібі жиі бұзылады, графиктерді құру кезінде қателіктер жіберіледі, материал негізсіз жеңілдетілген, қарабайыр немесе керісінше, терминдер мен символизммен шамадан тыс жүктеледі.
Функция ұғымын енгізу-бұл тұжырымдаманың барлық компоненттері туралы олардың өзара байланысында және оның математикада және оның қосымшаларында атқаратын рөлі туралы идеяларды қалыптастырумен аяқталатын ұзақ процесс. Бұл процесс негізгі үш бағыт бойынша жүргізіледі:
- функция туралы қолда бар түсініктерді ретке келтіру, функционалдық сызыққа тән ұғымдар жүйесін өрістету (тапсырма тәсілдері және функциялардың жалпы қасиеттері, графикалық координаталық әдіс негізінде анықтау аймағын, мәндер аймағын, өсуді және т. б. түсіндіру);
- жеке функциялар мен олардың сыныптарын терең зерттеу;
- функция идеясын және функциямен кең іс-қимыл жүйесін қосу арқылы алгебраның қосымшалар аймағын кеңейту.
Осы бағыттардың біріншісі мектеп алгебрасының курсында басқаларға қарағанда ертерек көрінеді.
Осы бағытты жүзеге асыруда функция ұғымына кіретін маңызды идеяны -- дәлел мен функцияның белгілі бір мәніне сәйкестіктің бірегейлігін ассимиляциялауға маңызды орын беріледі. Бұл мәселені қарастыру үшін функцияны орнатудың әртүрлі тәсілдері қолданылады.
Көбінесе математикада және оның қосымшаларында функция тапсырмасы формула бойынша қолданылады. Барлық басқа әдістер бағынышты рөл атқарады. Сондықтан бірнеше осы әдістермен турашқы танысқаннан кейін оқытудың негізгі бағыты олардың өрнегінің стандартты алгебралық формасы бар функциялар мен сыныптарға бағытттуран. Алайда, тұжырымдаманы енгізген кезде функцияны тағайындаудың әртүрлі тәсілдерін салыстыру маңызды рөл атқарады. Біріншіден, бұл практикалық қажеттілікпен байланысты: кестелер де, графиктер де, әдетте, жазудың аналитикалық формасы бар функцияны белгілі бір жағдайларда ыңғайлы ұсынуға қызмет етеді. Екіншіден, бұл функция тұжырымдамасының барлық аспектілерін ассимиляциялау үшін маңызды. Формула функцияны тиісті көріністер мен операциялар жүйесіне қосу арқылы ғана білдіреді, және бұл жүйе функция тұжырымдамасының әртүрлі компоненттерін табиғи түрде әр түрлі құралдармен көрсетуге болатындығында.
Функция тапсырмасының аудармасын ұсынудың бір формасынан екіншісіне қолдану функция ұғымын енгізуде қажетті әдістемелік әдіс болып табылады.
Бұл техниканы жүзеге асыру осындай аударманың барлық жағдайларын ұсынатын тапсырмалар жүйесін қолданудан тұрады. Егер сіз функцияны ұсынудың негізгі тәсілдерімен -- формуламен, графикпен, кестемен шектелсеңіз, онда сіз жаттығулардың 6 түрін аласыз, оларда көрініс формасы өзгереді, ал 3 -- те ол сол күйінде қалады. Біз бірінші типтегі тапсырмаларға мысалдар келтіреміз -- көрініс формасын өзгерту:
а) у = 4х+1 функциясының графигін интервалда бейнелеу.
б) аргумент үшін бірнеше мән алып, есептеу арқылы сандар квадраттарының кестесі қаншалықты дәл екенін тексеріңіз: x=1,35; 2,44; 9,4; 7; 6,25.
в) суретте координаталық жазықтықтағы атмосфералық қысымды бақылау нәтижелерін білдіретін нүктелер көрсетілген.
Осы нүктелерді тегіс сызықпен жтурау арқылы 12=T=18 аралығындағы қысымның уақытқа тәуелділік графигін құрыңыз.
Біз осы тапсырмалармен жұмыс істеу әдістемесін функция тұжырымдамасымен турашқы танысу кезеңінде ғана қарастырамыз, басқа кезеңдерде ол мүлдем өзгеше болуы мүмкін. Қарастырылған кезеңде оқушылар сызықтық функция графигінің жалпы түрін әлі білмейді (а тапсырмасы). Сондықтан y=4X+1 функциясының графигін олар тек нүктелер бойынша құра алады. Мұғалім нүктелерде функцияның толық графигін құруға болмайтындығына назар аудара алады, егер ол шексіз жиынтықта анықталса, бірақ бұл нүктелер түзу сызықта орналасқандығы байқалады; бұл ескерту дұрыс екендігі белгілі болды. Осылайша, материалды әрі қарай зерттеумен байланыс орнатуға болады. Нүктелердегі функцияның графигін құру әдісі в) тапсырмасымен суреттелген; тапсырманың нақты мазмұнын қолдана отырып, мұғалім студенттер ұсынатын графиктердің нақты позициядан өзгеше болуы мүмкін екенін, бірақ іс жүзінде бұл әдісті жиі қолдану керек (интерполяция). б) тапсырмасында функционалды көріністердің сандық жүйемен -- дәл және жуық сандық мән ұғымдарымен байланысын атап өтуге болады. Графиктерді салу кезінде оларды салыстырумен үнемі айналысу керек, өйткені диаграммаға нүктелерді тек шектеулі дәлдікпен қолдануға болады.
Қазіргі уақытта мектептегі функция ұғымын зерттеуде екі негізгі тәсіл басым: индуктивті және дедуктивті. Тарихи тұрғыдан туранда, олар білім берудің мақсаттары мен міндеттеріне толық сәйкес келеді, сондықтан оларға математиканы, оның ішінде мектептердің орта сыныптарындағы функцияларды оқығанда артықшылық беріледі.
7-сыныпта функция ұғымын зерттеуге индуктивті тәсіл қалай жүзеге асырылады:
"Іс жүзінде біз әртүрлі шамалар арасындағы тәуелділіктерді жиі кездестіреміз. Мысалы, шеңбердің ауданы оның радиусына байланысты, металл жолақтың массасы оның көлеміне және металдың тығыздығына байланысты, тікбұрышты параллелепипедтің көлемі оның ұзындығына, еніне және биіктігіне байланысты.
Болашақта біз екі шаманың арасындағы байланысты зерттейтін боламыз.
Мысалдарды қарастырайық
Бұдан кейін мысалдар шақырылған көрнекі түрде көрсетуге ғана баяндтуран материал.
Мысал 2. Алаңның ауданы оның жағының ұзындығына байланысты. Шаршының жағы a см, ал ауданы S см2 болсын .
A айнымалысының әр мәні үшін S айнымалысының сәйкес мәнін табуға болады.
Сонымен,
Егер a = 3 болса, онда S = 32 = 9;
Егер a = 15 болса, онда S = 152 = 225;
Егер a = 0,4 болса, онда S = 0,42 = 0,16.
S айнымалысының а айнымалысына тәуелділігі формула арқылы өрнектеледі
S = a2
(a 0 есебінің мағынасы бойынша).
Содан кейін тәуелді және тәуелсіз айнымалылардың турашқы анықтамасы беріледі:
"Мәндері ерікті түрде таңдтуран a айнымалысы тәуелсіз айнымалы деп аталады, ал мәндері таңдтуран a мәндерімен анықталатын s айнымалысы тәуелді айнымалы деп аталады".
3. Суретте күн ішіндегі ауа температурасының графигі көрсетілген.

Осы графиктің көмегімен уақыттың әр сәті үшін t (сағатпен), онда 0 Pound t Pound 24, тиісті p температурасын (Цельсий градусында) табуға болады. Мысалы,
егер t = 6 болса, онда p = -2;
егер t ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.