Кері тригонометриялық функция

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

Ф-УЧ-51

Қазақстан Республикасының білім және ғылым министрлігі
Қарағанды Bolashaq жоғарғы колледжі

КУРСТЫҚ ЖҰМЫС
Пән: математиканы оқыту теориясы мен әдістемесі

Тақырыбы: 10-11 сыныптарда алгебра және анализ бастамаларын оқыту әдістемесі

Орындаған: Алдабаев Б.Ж.
Жетекші: Жақыпбаева Г.Е.

Тіркеу №__________
Бағасы ____________
Қол ______________

Қарағанды 2021
МАЗМҰНЫ
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
І. 10- сыныпта алгебра және анализ бастамаларын оқыту әдістемесі
1.1 Тригонометриялық функциялар, олардың қасиеттері және графиктері ... ..5
1.2 Кері тригонометриялық функция ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...11
1.3 Туындыны және оның қолданылуы ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ...13
ІІ. 11-сыныпта алгебра және анализ бастамаларын оқыту әдістемесі
2.1 Комплекс сандар ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..16
2.2 Көрсеткіштік және логарифмдік теңдеулер мен теңсіздіктер ... ... ... ... ... .20
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..27
Қолданылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 29

КІРІСПЕ
Қазіргі ғылым, оның іргетасы - математика заманымыздың аса мәдени құбылысы, жалпы өркениетіміздің бөлінбес маңызды бір бөлігі болып отыр.
Математиканы оқыту әдістемесі - математика пәнінің ерекшеліктеріне негізделген оқу - тәрбие жүйесі жайындағы ғылым. Бұл жүйені меңгеру математиканы оқыту мен математика пәні арқылы оқушыларды тәрбиелеу ісін ұйымдастыруға мүмкіндік береді.
Математиканы оқыту әдістемесі мұғалімнің оқу материалдарын беру, оқушылардың математикалық білімді саналы меңгеру және алған білімін практикада қолдану іскерліктерін шыңдау әдістері мен құралдарын тағайындайды.
Математиканы оқытудың негізгі мақсаттары жалпы білім беру, тәрбиелік және практикалық болып саналады.
Математиканы оқытудың жалпы білім беру мақсаты мұғалімге келесі талаптар қойылады: мектеп программасы анықтайтын математикалық білімнің, іскерлік пен машықтың барлық жүйесін оқушылардың терең және саналы меңгеруін қамтамасыз ету; математикалық тілді меңгеруге үйрету; оқушылардың нақтылы шындықты математикалық әдістермен меңгеруіне көмектесу.
Математиканы оқытудың тәрбиелік мақсаты: оқушылардың дүниеге ғылыми көзқарасын қалыптастыру, табиғатты ғылыми жағынан танудың негізгі заңдылықтарының математикадағы көрінісін бейнелеу; оқушыларға адамгершілік және эстетикалық тәрбие беру.
Математиканы оқытудың практикалық мақсаттары: оқушыларды алған теориялық білімдерін практикада қолдана білуге, практикалық есептерді шығаруға, сондай-ақ математиканы физикаға, химияға т.б. жаратылыстану пәндерінде қолдана білуге үйрету; математикалық құрал-жабдықтарды пайдалануға баулу; оқушылардың өздігінен білім алуына көмектесу [1].
Мектеп математика курсын оқытудың ең маңызды мақсаттарының бірі - алгебраның қолданбалы мүмкіндіктерін ашу. Математикалық технология немесе алгебралық мазмұнды есептерді шешу барысында оқушылар алгебра ұғымдар мен заңдылықтарды тереңірек түсініп, ұғынып, сонымен қатар кәсіби даярлықтың негіздерін меңгереді. Оқушылардың ойлау қабілеттерін дамытуда, оларды тәрбиелеуде, біліктері мен дағдыларының қалыптасуында, алгебраның практикамен байланысын көрсетуде есептің алатын орны өте зор. Оқушылардың дүниетанымына әр оқу пәні өз үлесін қосып отырады. Соның ішінде алгебраны оқыту барысында сабақтас пәндерден және нақтылы өмірден оқушыларға түсінікті түрде келтірген деректер ғылыми білімдердің пайда болу негізін, қоршаған ортаның табиғат құбылыстарының танымалы жеке пәндердің алгебралық ұғымдары мен абстрактілі жағдайларын оңай сезіне біледі.
Математика пəнінің, оның ішінде Алгебра және анализ бастамалары курсының жоғары сынып оқушыларының басым көпшілігі үшін айтарлықтай қиындықтар туғызатын. Осы қиыншылықтың түбіріне үңілсек, ол көпшілік жағдайда оқушылардың алгебралық формулаларды қабылдай алмауы сол формулаларды қолдана алмауы, есептің мәтінің түсінбеуі, логикалық ойлау қабілеттері дамымағаны болып келеді. Аталған факторлардың барлығы математика курсының басында оқушылардың алгебралық мәліметтерді дұрыс қабылдамауына алып келеді.
Алгебра және анализ бастамаларының есептерін шығару оқушының логикалық ойлау қабілетін арттырып, және сол қабілетті қолдана білуге де үйретеді. Алгебра және анализ бастамаларының есептерін шешуде жаңа компъютерлік технологияны (жаңа ақпараттық технология) қолдану оқушыларға жаңа ақпараттарды түсіндіруді жеңілдетеді және олармен жұмыс істеу дағдылары мен іскерліктерін дамытады.
Жұмыстың мақсаты: Алгебра және анализ бастамаларын оқыту әдістемесімен танысып, тәжірибеде қолдану.
Жұмыстың міндеттері:
* Алгебра және анализ бастамаларын жан-жақты зерттеп, элементтері мен формулаларын қолдануды үйрену;
* Алгебра және анализ бастамаларының есептерін шешкенде ыңғайлы әрі оңай жолын таңдап, есеп шығаруда қолдануға үйрету;
* Оқушылардың логикалық ойлау қабілетін, формулаларды қолдану дағдыларын, алгебралық (математикалық) білімдерін әдіс- тәсілдерді зерттеу.
* Алгебра және анализ бастамаларының есептерін шығару ерекшеліктерін талдау.
Зерттеу пәні: Математиканы оқыту әдістемесі.
Зерттеу әдістері: Курстық жұмысты жазу барысында жинақтау, салыстыру, сараптау, талдау, зерттеу әдістері пайдаланылады.
Жұмыстың құрылымы: жұмыс кіріспеден, екі тараудан, қортынды және қолданылған әдебиеттер тізімінен тұрады. Курстық жұмыс 29 беттен тұрады

І. 10 - сыныпта алгебра және анализ бастамаларын оқыту әдістемесі
1.1 Тригонометриялық функциялар, олардың қасиеттері және графиктері
Оқушылар 9 - сыныпта алгебра курсынан тригонометриялық функциялардың анықтамаларын, формулаларын және кейбір қасиеттерін оқыды. Осы мағлұматтарды ескеріп және график салудың алгоритмін қолдана отырып, тригонометриялық функциялардың графиктерін салуды үйренеді [2].
Сабақты түсіндіру барысында көрнекіліктерді кеңінен қолданған дұрыс. Ол үшін алдын ала дайындалған мынандай көрнекілікті қолдануға болады.
Функция y=sinx
1. Dsinx=(-infinity;+infinity)
2. sinx=-sinx - тақ функция sinx+2kPI=sinx, k∈Z - периодты функция
3. Ox өсімен x=kPI, k∈Z нүктелерінде, ал Oy өсімен O(0;0) нүктесінде қиылысады.
4. x∈2kPI;2k+1PI--sinx0;
x∈2k-1PI;2kPI--sinx0;
5. x∈-PI2+2kPI;PI2+2kPI - функция өспелі;
x∈-PI2+2kPI;3PI2+2kPI - функция кемімелі;
6. x1=PI2+2kPI, k∈Z - max нүктелері, sinx1=1;
x2=PI2+2kPI, k∈Z - min нүктелері, sinx2=1;

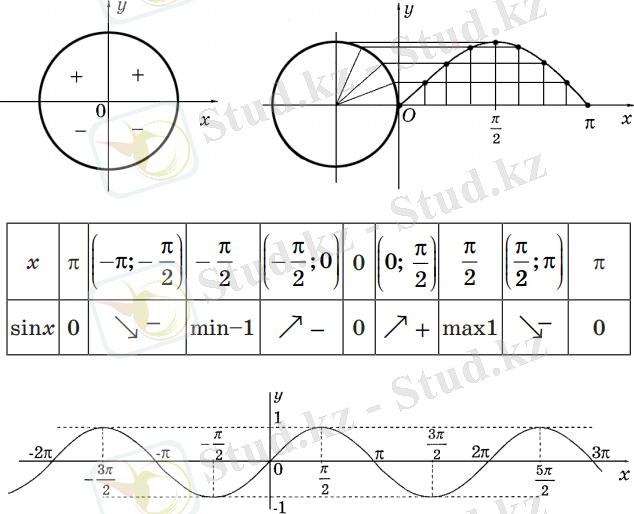
Осындай көрнекіліктерді оқушыларға басқада тригонометриялық функциялары үшін да жасауды тапсыру керек. Бұл көрнекіліктердің барлығы да әр оқушының қысқаша конспектісінде болғанын қадағалау қажет.
Енді әрбір тригонометриялық функцияның графигін салуға тоқталайық.
I. y=sinx функциясын қарастырайық.
y=sinx функциясының графигін салу үшін алдымен оның 0;2PI кесіндісіне тиісті бөлігін саламыз. Ол үшін абсцисса осінде абсциссасы 2PI(PI=3,14) болатын нүктені белгілейміз және синустың анықтамасын қолданамыз. Оу осінің сол жағына центрі Ох осінде жататын бірлік шеңбер саламыз және ордината осіне (0; -1) және (0; 1) нүктелерін белгілейміз. Бірлік шеңбер мен 0;2PI кесіндісін тең 16 бөлікке бөлеміз

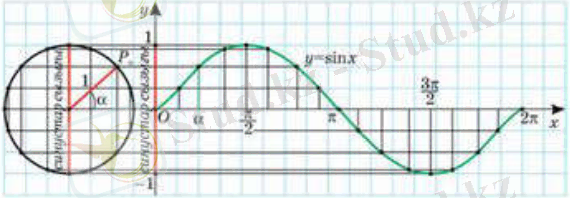
Бірілік шеңберде Pα нүктесін белгілейміз және осы нүкте арқылы абсцисса осіне параллель түзу жүргіземіз. Осы түзу мен x=α түзуінің қиылысу нүктесі y=sinx функциясы графигінің нүктесі болып табылады. Нүктенің ординатасы Pα нүктесінің ординатасымен бірдей, анықтама бойынша sinx-Pα нүктесінің ординатасы.
y=sinx функциясының графигін барлық сан түзуінде салу үшін оның 0;2PI кесіндісінде салынған бөлігін Ох осі бойымен 2PIn-ге (мұндағы n - бүтін сан) параллель жылжытамыз.
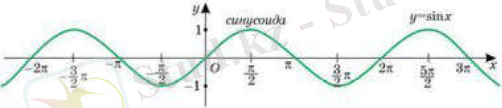
y=sinx функциясының графигі синусоида деп аталады.

y=sinx функциясының қасиеттері:
1) Анықталу облысы - (-infinity;+infinity) сан аралығы,яғни x∈R .
2) мәндер жиыны [-1; 1] кесіндісі, яғни y∈ [-1; 1].
3) y=sinx функциясы шектелген: sinx 1.
4) y=sinx функциясы периодты, оның ең кіші периоды 2PI sin (x + 2PIn) = sin x, мұндағы n - бүтін сан.
5) y=sinx функциясы тақ функция: sin (-x) = - sin x. Оның графигі координаталар басына қарағанда симметриялы.
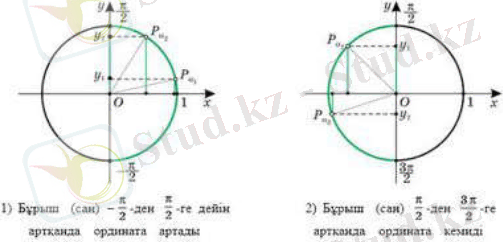
6) y=sinx функциясы 2PIn;n+2PIn аралығында оң мәндерді және PI+2PIn;2PI+2PIn, мұндағы n - бүтін сан, аралығында теріс мәндерді қабылдайды.
7) y=sinx функциясы -PI2+2PIn; PI2+2PIn аралығында өседі және PI2+2PIn; 3PI2+2PIn аралығында кемиді, мұндағы n - бүтін сан.
Қарастырылған қасиетті бірлік шеңбердің көмегімен көрсетуге болады.

8) y=sinx функциясының экстремумдары: xmin=-PI2+2PIn, xmax=PI2+2PIn функцияның ең үлкен және ең кіші мәндері: yең үлкен=1, yең кіші=-1.
Мысал: y=sinx+2 функциясының графигін салайық.
Шешуі. Алдымен y=sinx функциясының графигін саламыз. Ол үшін A, B, C, D, O, E, F, K, L, M, N нүктелерін белгілейміз және оларды қисық сызықпен қосамыз. Одан кейін әрбір нүктені ордината (Oy) осі бойымен жоғары 2 бірлікке жылжытамыз. Сонда A1, B1, C1, D1, O1, E1, F1, K1, L1, M1, N1, нүктелерін аламыз және оларды қисық сызықпен қосамыз.

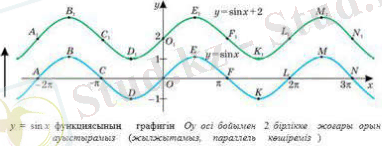
y=sinx функциясының графигін Oy осі бойымен 2 бірлікке жоғары орын ауыстырамыз (жылжытамыз параллель көшіреміз)
y=Afkx+b түріндегі функцияның периодтылығы. Егер y=fx функциясы периодты және периодты Т - ға тең болса, онда y=Afkx+b, мұндағы A, k, b- нақты сандар және k!=0, функциясы да периодты болады және оның периодты Tk - ға тең болады.
Мысалы2:y=sin3x функциясының периодты 2PI3 - ға, y=sinx2 функциясының периоды 4PI-ге тең.
II. y=cosx функциясын
y=cosx функциясының графигін салу үшін cosx=sin⁡(x+PI2) келтіру формуласы қолданамыз. Сондықтан y=cosx функциясының графигі y=sinx функциясының графигін Ox осі бойымен солға қарай PI2 бірлікке параллель көшіру арқылы алынады.

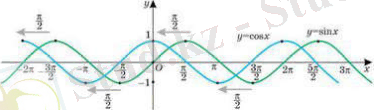
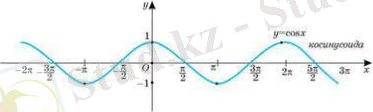
y=cosx функциясының графигі косинусоида деп аталады.
y=cosx функциясының қасиеттері:
1) Анықталу облысы - (-infinity;+infinity) сан аралығы,яғни x∈R .
2) мәндер жиыны [-1; 1] кесіндісі, яғни y∈ [-1; 1].
3) y=cosx функциясы шектелген: cosx 1.
4) y=cosx функциясы периодты, оның ең кіші периоды 2PI-ге тең cos (x + 2PIn) = cosx, мұндағы n - бүтін сан.
5) y=cosx функциясы жұп функция: cos (-x) = cos x. Оның графигі ордината осіне қарағанда симметриялы.
6) y=cosx функциясы -PI2+2PIn; PI2+2PIn аралығында оң мәндерді және PI2+2PIn; 3PI2+2PIn, мұндағы n - бүтін сан, аралығында теріс мәндерді қабылдайды.
7) y=sinx функциясы 2PIn;n+2PIn аралығында өседі және PI+2PIn;2PI+2PIn, аралығында кемиді, мұндағы n - бүтін сан.
Қарастырылған қасиетті бірлік шеңбердің көмегімен көрсетуге болады.

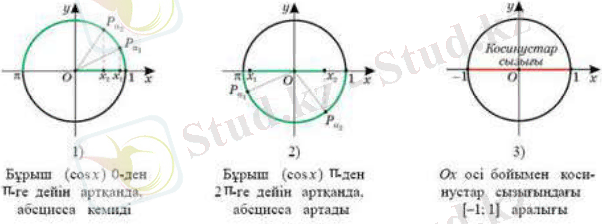
Косинустар сызығы дегеніміз - Ox осінің -1;1 кесіндісі
8. y=cosx функциясының экстремумдары: xmin=-PI+2PIn, xmax=2PIn функцияның ең үлкен және ең кіші мәндері: yең үлкен=1, yең кіші=-1.
Мысал: -PI;PI кесіндісіне y=cos2x функциясының графигін салайық.
Шешуі. Алдымен y=cosx функциясының графигін -2PI;2PI кесіндісіне саламыз. Ол үшін T, A, B, C, M, K, P, H, D нүктелерін белгілейміз және оларды қисық сызықпен қосамыз. Одан кейін әрбір нүктені абсцисса осі бойымен 2 есе сығамыз. Сонда ординаталары T, A, B, C, M, K, P, H, D нүктелерінің ординаталарымен бірдей, абсциссалары 2 есе кем T1, A1, B1, C1, M1, K1, P1, H1, D1 нүктелерін қисық сызықпен қосып, көрсетілген аралықта берілген функцияның графигін аламыз.

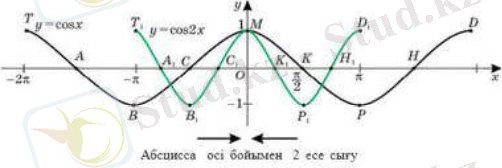
Графиктен y=cos2x функциясының периоды PI-ге тең екенін көреміз.
y=tgx, y=ctgx функцияларының графиктері және қасиеттері.
ІІІ. y=tgx функциясы
Бірлік шеңберге Р0 нүктесі арқылы l жанамасын жүргіземіз (13.1- сурет)

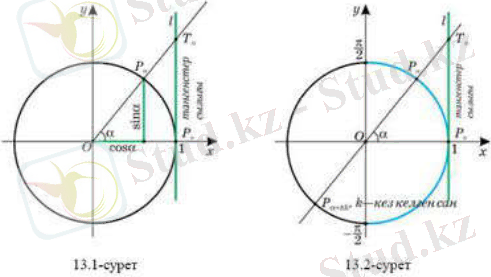
α саны cosα!=0 орындалатындай кез келген сан болсын. Онда Р0 cosα;sinα нүктесі ордината осіне тиісті емес, сондықтан OPα түзуі l жанамасын абсциссасы 1-ге тең болатын Тα нүктесінде қияды.
Осы нүктенің ординатасын табайық. Анықтама бойынша tgα=sinαcosα=TαP01, онда TαP0=tgα. Сонымен OPα және l түзулерінің қиылысу нүктелерінің ординаталары tgα-ға тең.
l түзуін тангестер сызығы деп атайды (13.2- сурет)
y=tgx функциясы периодты және периодты PI-ге тең. y=tgx функциясының графигін салу үшін алдымен оның -PI2;PI2 аралығына тиісті бөлігін саламыз. Ол үшін абсцисса осінде абсциссасы -PI2 және PI2 (PI≈3,14) болатын нүктелерді белгілейміз және тангенстер осін қолданамыз. Oy осінің сол жағынан центрі Ox осінде жататын бірлік шеңбер сызамыз. Бірлік шеңбер мен -PI2;PI2 кесіндісін тең 8 бөлікке бөлеміз.

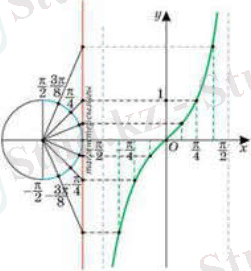
-3PI8;-PI4;-PI8;0;PI8;PI4;3PI8 бұрыштарына сәйкес нүктелерді бірлік шеңберде белгілейміз. Осы бұрыштар үшін y=tgx функциясының мәндерін тангенстер сызығы арқылы табамыз. Ол үшін координаталар басы және әрбір белгіленген нүкте арқылы тангенстер осіне дейін түзу жүргіземіз. Тангенстер осімен қиылысу нүктесі y=tgx функциясы графигінің нүктесінің ординатасы болып табылады.
y=tgx функциясы графигін барлық сан түзуінде салу үшін оның -PI2;PI2 кесіндісінде салынған бөлігін Ox осі бойымен PIn-ге параллель жылжытамыз.

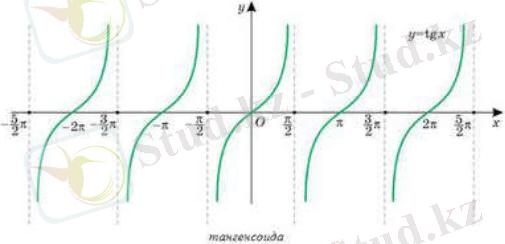
y=tgx функциясының графигін тангенсоида деп аталады.
y=tgx функциясының қасиеттері:
1) Анықталу облысы - PI2+PIn сандарынан басқа α-ның барлық мәндері.
2) мәндер жиыны [-infinity; infinity] сан аралығы, яғни y∈ [-infinity;infinity].
3) y=tgx функциясы шектелмеген.
4) y=tgx функциясы периодты, оның периоды PI-ге тең tg(x+2PIn)=tgx, мұндағы n - бүтін сан.
5) y=tgx функциясы тақ функция: tg-x=-tgx. Оның графигі координаталар басына қарағанда симметриялы.
6) y=tgx функциясы PIn;PI2+2PIn аралығында оң мәндерді және -PI2+2PIn;PIn, мұндағы n - бүтін сан, аралығында теріс мәндерді қабылдайды.
7) y=tgx функциясы -PI2+PIn; PI2+PIn аралығында өседі
8) y=tgx функциясының экстремумдары мен ең үлкен және ең кіші мәндері болмайды.
IV. y=ctgx функциясы
y=ctgx функциясының графигін салу үшін y=ctgx=-tg(x+PI2) келтіру формуласын қолданамыз. Сондықтан y=ctgx функциясының графигін Ox осі бойымен солға қарай PI2 бірлікке параллель көшіру және Ox осіне қарағанда симметрияны қолдану арқылы алынады.

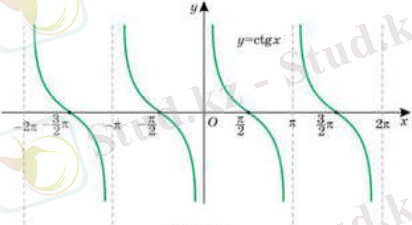
y=ctgx функциясының қасиеттері:
1) Анықталу облысы PIn сандарынан басқа α-ның барлық мәндері.
2) мәндер жиыны [-infinity; infinity] сан аралығы, яғни y∈ [-infinity;infinity].
3) y=ctgx функциясы шектелмеген.
4) y=ctgx функциясы периодты, оның периоды PI-ге тең ctg(x+2PIn)=tgx, мұндағы n - бүтін сан.
5) y=ctgx функциясы тақ функция: tg-x=-tgx. Оның графигі координаталар басына қарағанда симметриялы.
6) y=ctgx функциясы PIn;PI2+2PIn аралығында оң мәндерді және PI2+2PIn;PI+PIn, мұндағы n - бүтін сан, аралығында теріс мәндерді қабылдайды.
7) y=ctgx функциясы PIn; PI+PIn аралығында кемиді
8) y=ctgx функциясының экстремумдары мен ең үлкен және ең кіші мәндері болмайды.
Мысал: (0; PI) интервалында y=2ctgx функциясының графигін салайық.
Шешуі. Алдымен y=ctgx функциясының графигін (0; PI) интервалына саламыз. Ол үшін А, В, С нүктелерін белгілейміз және оларды қисық сызықпен қосамыз. Одан кейні ордината осі (Оу) бойымен 2 есе созамыз.
Енді абсциссалары А, В, С нүктелерінің абсциссаларымен бірдей, ординаталары 2 есе артық А1, В1 ,С1 нүктелерін аламыз және оларды қисық сызықпен қосамыз. Сонда көрсетілген аралықта берілген функцияның графигі шығады [3].

1.2 Кері тригонометриялық функция
Сабақтың кіріспе бөлігінде оқушылармен бірге кері функциялар жөніндегі жалпы мәліметтерді пысықтап, еске түсіріп алу керек. Оқушыларға әрбір тригонометриялық функцияның бірсарындылық аралықтарын көрсетуді ұсыну қажет. Осындай дайындық жұмыстарынан соң тақырыпты түсіндіру қиындыққа соқпайды.
Бұл тақырып материалдары математиканы тереңдетіп оқытатын сыныптар үшін арналған және кері тригонометриялық теңдеулер ұлттық бірыңғай тестілеу тапсырмаларында қарапайым теңдеулер түрінде ғана кездеседі. Сондықтан ең алдымен оқушылардың А тобы есептерін толық меңгерулеріне басты көңіл аудару қажет. Ал бұл есептер саны жеткіліксіз болып жатса, онда оқушының жеке нұсқасындағы а, b, c және d сандарын пайдаланып, қосымша мынадай есептерді қарастыруға болады.
y=arcsinx функциясының
Анықтама. y=sinx, x∈-PI2;PI2 функциясына кері функцияны арксинус функциясы деп атап, y=arcsinx,x∈-1;1 арқылы белгілейді.

y=arcsinx функциясының қасиеттері:

- Анықталу облысы: x∈-1;1
- Өзгеру жиыны: y∈-PI2;PI2
- Функция тақ, периодты емес, шектелген
- Графигі Ох және Оу осьтерін координаталар бас нүктесінде қияды
- Функция анықталу облысында бірсарынды өспелі

y=arccosx функциясының
Анықтама. y=cosx, x∈0;PI функциясына кері функцияны арксинус функциясы деп атап, y=arccosx,x∈-1;1 арқылы белгілейді
y=arccosx функциясының қасиеттері

- Анықталу облысы: x∈-1;1
- Өзгеру жиыны: y=0;PI
- Функция тақ емес, жұп та емес; периодты емес; шектелген.
- Графигі Ох осін х=1 нүктесінде және Оу осін y=PI2 нүктесінде қияды
- Функция анықталу облысы бірсарынды кемімелі.

y=arctgx функциясы
y=tgx функциясы -PI2;PI2 интервалында анықталған, бірсарынды өспелі және R жиынындағы өзінің барлық мәндерін қабылдайды. Демек -PI2;PI2 интервалындa y=tgx функциясына кері функция y=arctgx болады. y=arctgx функциясы x∈R жиынында анықталған, -PI2;PI2 интервалында өзгеретін бірсарынды өспелі функция.
Енді y=arctg функциясының қасиеттерін келтірейік:
1) функцияның анықталу облысы - барлық нақты сандар жиыны, x∈R;
2) мәндер жиыны -PI2; PI2 интервалы;
3) функция тақ, кез келген x үшін arctg-x=-arctgx;
4) функция бір сарынды өспелі.

Кез келген x үшін x=tg(arctgx) тепе-теңдігі орындалады, мұндағы x үшін -PI2arctgxPI2
y=arcctgx функциясы
y=ctgx функциясына кері функцияны анықтайық:
y=ctgx функциясы 0;PI интервалында анықталған, бірсарынды кемімелі және сол аралықта R жиынындағы өзінің барлық мәндерін қабылдайды. Осы интервалда y=ctgx функциясына y=arcctgx функциясы кері функция болып табылады. Онда y=arcctgx функциясы x∈R жиынында анықталған, 0;PI интервалында өзгеретін бірсарынды кемімелі функция

y=arcctgx функциясының қасиеттері.

1) анықталу облысы - барлық нақты сандар жиыны, x∈R
2) мәндер жиыны -0;PI аралығы;
3) функция жұп та тақ та емес;
4) функция бірсарынды кемімелі.

Кез келген x үшін x=ctgarcctgx, 0arcctg yPI, arcctg-x=PI-arcctg x тепе-теңдігі орындалады [3]
1.3 Туынды оның қолдануы
Математикада ең маңызды ұғымдардың бірі - функция туындысы ұғымы болып табылады. Туындылар және олардың функциялары математикалық анализ курсының ең негізгі бөлімі болып табылады.
Туынды ұғымы бастапқыда шек түрінде анықталады. Бұл жерде оқушыларға Шек терминін кезінде Ньютон еңгізгенін, оның lim белгіленуі - латынның limes (меже, шекара) деген сөзінің қысқарған түрі екенін түсіндіріп, айта кету керек.
Бірінші сабақта туынды ұғымын еңгізбес бұрын келесі есептерді қарастырған жөн. Олар: химиялық реакцияның жылдамдығы, токтың лездік күші, денелердің лездік жылдамдығын табу, дененің жылуы, қисыққа жанама жүргізу т.с.с. солардың кейбіреулеріне тоқталайық. Функция туындысы түсінігін лездік жылдамдықты анықтау мен жанама жөніндегі есептерді шешуден бастайды.
Бұл тақырып, функцияның нүктедегі шегі мен үздіксіздігіне ұқсас, оқушылардың жете ұғынуына қиын соғатын тақырыптардың бірі [4].
Анықтама. Функцияның анықталу облысынан алынған екі аргументтің айырымының мәні функция аргументінің өсімшесі деп аталады.
Аргумент өсімшесінің белгіленуі: ∆x Жазылуы: x2-x1=∆x.
Анықтама. Мәндер жиынынан алынған функцияның екі мәнінің айырымы функцияның өсімшесі деп аталады.
Функция өсімшесінің белгіленуі: ∆у Жазылуы: ∆у=f(x2)-f(x1).
Анықтама. Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесінің нөлге ұмтылғандағы шегі бар болса, ол шек функцияның туындысы деп аталады.
f'x=lim∆x--0∆y∆x=lim∆x--0fx+∆x-f( x)∆x
Анықтама. Шектелген туындысы бар функция нүктеде дифференциалданатын функция деп аталады.
Анықтама. Функцияның туындысы табу амалын дифференциалдау деп айтады.
Туындыны табу ережелері
Теорема. Екі функцияның қосындысының (айырымының) туындысы туындылардың қосындысына (айырымына) тең:
(f(x)+-g(x))'=f'(x)+-g'(x)
Айырымды алгебралық қосындымен алмастыруға болады, демек берілген формуланы былай жазуға болады.
(u+v)'=u'+v'
Дәлелдеу. (u+v)'=lim∆x--0∆(u+v)∆x=lim∆x--0∆ u+∆v∆x=u'+v'
Дәлелденген формула қосылғыштар саны екіден артық болған жағдайда ақиқат.
Мысал1. gx=x+x2-3 функциясының туындысы табайық.
Шешуі: y=gx функциясы дифференциалданатын үш функцияның қосындысын береді. Сондықтан g'x=(x+x2-3)'=(x)'+(x2)'+-3'=1+2x+0 =1+2x
Теорема. Екі функцияның көбейтіндісінің туындысы
(fx*g(x))'=f'x*g'x+f'x*g'x формуласымен анықтайды.
Қысқаша формула (uv)'=u'v+uv' түрінде жазылады
Дәлелдеу. (uv)'=lim∆x--0∆(uv)∆x=lim∆x--0u(x 0+∆x)v(x0+∆x)-uv∆x= ux0+∆x=u+∆uvx0+∆x=v+∆v=lim∆x--0(u+ ∆u)(v+∆v)-uv∆x=lim∆x--0∆uv+(∆v)u-( ∆u)(∆v)∆x=u'v+v'u+u'lim∆x--00∆v=u' v+v'u
Мысал2. fx=5x
Шешуі. y=fx функциясы 5 санынан (тұрақтыдан) және дифференциалданатынын y=1x функциясының көбейтіндісінен тұрады. Сондықтан f'x=(5x)'=(5*1x)'=5*(1x)'+1x*5'=5*( 1x)'+1x*0=5*-1x2=-5x2;
Теорема. Дифференциалданатын y=fx және y=gx, мұндағы gx!=0, функциялары қатынасының туындысы (fxgx)'=f'x*gx-fx*g'(x)g2(x) формуласымен табылады.
Қысқаша жазылуы: (uv)'=u'v-uv'v2(v!=0)
Дәлелдеу. (uv)'=lim∆x--0∆uv∆x=∆uv=u+∆uv+∆v-u v=lim∆x--0∆uv-∆vu∆xuv+∆v=lim∆x--0 ∆u∆x*1v+∆v-lim∆x--0∆v∆x*uvv+∆v=u'v -v'uv2=u'v-v'uv2
Тригонометриялық функциялардың туындысы

yx=sinx
(sinx)'=cosx
yx=cosx
(cosx)'=-sinx

yx=tgx
(tgx)'=1cos2x
yx=ctgx
(ctgx)'=-1sin2x

Екінші туынды және оның физикалық мағынасы
Анықтама. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.