Дифференциалдық геометрия: қисықтар мен беттер теориясы бойынша есептер жинағы (оқу құралы)


ҚОСТАНАЙ МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ
Жаратылыстану-математика факультеті
Физика-математикалық және жалпы техникалық пәндер кафедрасы
Асқанбаева Ғ. Б.
Дифференциалдық геометриядан
есептер жинағы
Оқу құралы
Қостанай
2016
ӘОЖ 514. 7(075. 8)
КБЖ 22. 151 я73
А 88
Құрастырушы:
Асқанбаева Ғ. Б. - физика-математикалық және жалпы техникалық пәндер кафедрасының аға оқытушысы
Сын пікір берушілер:
Ысмағұл Р. С. - ф-м. ғ. кандидаты (А. Байтұрсынов атындағы ҚМУ, информатика және математика кафедрасының доценті)
Калжанов М. У. - ф-м. ғ. кандидаты (ҚМПИ, информатика және компьютерлік технологиялар кафедрасының доценті)
Асқанбаева Ғ. Б.
Дифференциалдық геометриядан есептер жинағы: оқу құралы / Ғ. Б. Асқанбаева. - Қостанай, 2016. - 99 б.
ISBN 978-601-7839-51-2
Оқу құралында дифференциалдық геометрияның қисықтар және беттер теориясы қарастырылған. Пәннің әрбір тарауы үшін қысқаша теориялық мәліметтермен қоса, есептер және олардың шешу жолдары көрсетілген. Студенттерге өз білімдерін тексеру үшін тест тапсырмалары, өздік тапсырмалар ұсынылған.
Оқу құралы 5В010900-Математика мамандығы бойынша оқитын студенттерге арналған.
ӘОЖ 514. 7(075. 8)
КБЖ 22. 151 я73
Қостанай мемлекеттік педагогикалық институтының
ғылыми кеңесінің шешімімен баспаға ұсынылады
ISBN 978-601-7839-51-2
© Асқанбаева Ғ. Б., 2016
МАЗМҰНЫ
ӨЗІН-ӨЗІ ТЕКСЕРУГЕ АРНАЛҒАН ТЕСТ ТАПСЫРМАЛАРЫ . . .
ТЕСТ ТАПСЫРМАЛАРЫНЫҢ ЖАУАПТАРЫ . . .
67
84
КІРІСПЕ
Дифференциалдық геометрия - геометрияның геометриялық бейнелерді математикалық талдау тәсілімен зерттейтін бөлімі. Дифференциалдық геометрияда алдымен қисықтар мен беттердің шектеусіз аз үйірлерінің қасиеттері айқындалады, содан кейін қисық пен беттің тұтас тұлғасындағы ерекшеліктері анықталады. Дифференциалдық геометрия математикалық талдаумен тығыз байланысты және онымен қатар дамып келді. Математикалық талдаудың кейбір түсініктері геометрияға байланысты шыққан. Мысалы, туынды түсінігі жанама түсінігінен, интеграл түсінігі аудан және көлем түсініктеріне байланысты шыққан. Дифференциалдық геометрияның шығу кезеңі ХҮІІ ғасыр деп есептелінеді және де оның шығу тарихы Л. Эйлер, Г. Монж есімдерімен байланысты. 1759 жылы «Анализдың геометрияға қосымшасы» атты Г. Монждың беттер теориясы бойынша шығармасы шықты.
1827 жылы К. Гаусс «Қисықтар мен беттер туралы жалпы зерттеулер» атты еңбегін жарыққа шығарды. Бұл еңбегінде ол беттер теориясының негізін салып берді. Осы кезеңнен бастап, дифференциалдық геометрия математикалық талдаудың қосымша саласы емес, жеке ғылым болып дами бастады.
Ал 1826 жылы Н. И. Лобачевскийдің евклидті емес геометрияны ашуы, бүкіл геометрияның дамуынада үлкен роль атқарды.
Дифференциалдық геометрияның зерттеу аппараты ретінде дифференциалдық есептеулер қолданылады. Геометриялық объектілер ретінде қисықтар мен беттер қарастырылады. Осы объектілерді ақырсыз кішкене бөліктерде зерттеу қисықты түзу, беттің бөлігін жазықтық ретінде қарастыруға мүмкіндік береді.
Аталған оқу құралында дифференциалдық геометрияның негізгі бөлімдері бойынша, атап айтқанда қисықтар және беттер теориясы бойынша үш жүзден артық жаттығулар мен есептер келтірілген. Әр параграфтың басында қысқаша теориялық мәліметтер беріліп, есептердің шығару жолдары көрсетілген. Студенттерге өз білімдерін тексеру үшін тест тапсырмалары, өздік тапсырмалар ұсынылған. Тест тапсырмалары жауаптармен қамтамасыз етілген.
Әдістемелік құралдың соңында әрбір есепке жауаптар берілген. Қиындығы жоғары есептердің шешу жолдары, ал кейбір есептерді шешу үшін нұсқаулар келтірілген.
«Дифференциалдық геометриядан есептер жинағын » осы пәнді игеруге арналған оқу құралы ретінде қолдануға болады. Оқу құралы 5В010900- Математика мамандығы бойынша оқитын студенттерге арналған.
I ҚИСЫҚТАР ТЕОРИЯСЫ
1. 1 Скаляр аргументке тәуелді вектор-функция
Анықтама:
a < t < b аралық берілсін. Егер tє(a, b) әрбір мәніне
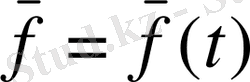 векторының анықталған мәні сәйкестендірілсе, онда осы аралықта скаляр аргументке тәуелді вектор-функция берілді дейміз.
векторының анықталған мәні сәйкестендірілсе, онда осы аралықта скаляр аргументке тәуелді вектор-функция берілді дейміз.

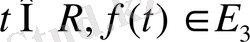
Вектор-функция үшін үзіліссіздік ұғымы скаляр-функция сияқты енгізіледі.
Анықтама:
Егер
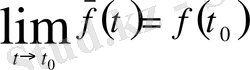 орындалса, онда
орындалса, онда
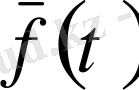 вектор-функция
вектор-функция
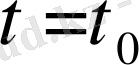 нүктесінде үзіліссіз деп аталады.
нүктесінде үзіліссіз деп аталады.
Анықтама:
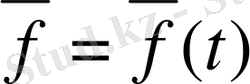 вектор-функцияның туындысы деп
вектор-функцияның туындысы деп
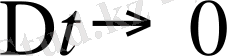 ұмтылғандағы
ұмтылғандағы
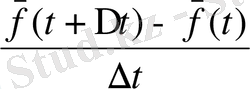 қатынасының шегі аталады.
қатынасының шегі аталады.
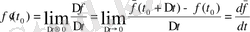 .
.
Вектор функцияны дифференциалдау ережелері
1 теорема: Вектор-функциялардың қосындысының туындысы олардың туындылардың қосындысына тең.
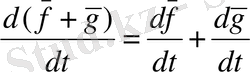 (1)
(1)
2 теорема: Вектордың скалярға көбейтіндісі, векторладың скалярлы және векторлық көбейтіндісі скалярлық анализдің ережесі бойынша дифференциалданады.
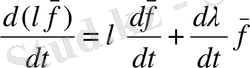 (2)
(2)
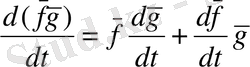 (3)
(3)
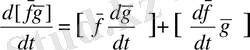 (4)
(4)
(3) формуладан скаляр квадратты дифференциалдау ережесі шығады.
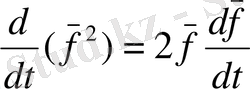
3 теорема: Векторлардың аралас көбейтіндісі келесі ереже бойынша дифференциалданады.
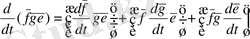 (5)
(5)
4 теорема: Тұрақты вектордың туындысы нөлге тең.
Вектор-функцияның туындысының координаталарын табу
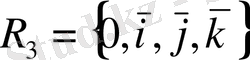 ортонормаланған базис берілсін.
ортонормаланған базис берілсін.
 вектор-функция.
вектор-функция.
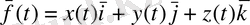
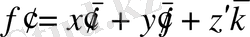
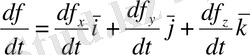
Координатаның туындысы дифференциалданатын вектор-функцияның сәйкес координаталарының туындысына тең.
Мысалдар:
а)
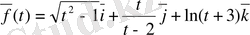 вектор функция үшін скаляр функцияларды анықтау керек және оның анықталу облысын көрсету керек.
вектор функция үшін скаляр функцияларды анықтау керек және оның анықталу облысын көрсету керек.
Шешуі: Вектор-функция координаталық түрде берілген, сондықтан скаляр функцияларды көрсетуге болады:
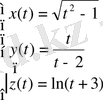
Вектор функцияның анықталу облысын табу үшін, x(t), y(t), z(t) функцияларының әрқайсысының анықталу облысын тауып, теңсіздіктер жүйесін щешу керек.
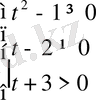 ,
,
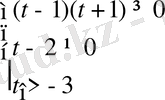
Әрбір теңсіздікті шешіп, координаталық түзуде аралықтардың қиылысуын табамыз

Жауабы:
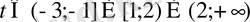 .
.
ә) Келесі вектор-функциялар берілген:
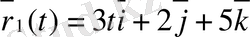 ,
,
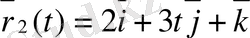 . Осы функциялардың скаляр көбейтінділерінің туындысын табу керек.
. Осы функциялардың скаляр көбейтінділерінің туындысын табу керек.
Шешуі: Екі вектор-функцияның скаляр көбейтіндісінің туындысын табу үшін, вектор-функцияны дифференциалдау ережесін қолданамыз:
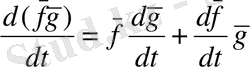
Осы формулаға берілген вектор-функцияларды қойып, келесі теңдікті аламыз:
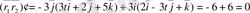 .
.
Жауабы:
 .
.
Өз бетімен шығаруға арналған есептер
№1-2 Келесі вектор функциялар үшін скаляр функцияларды анықтау керек және оның анықтау облысын көрсету керек.
№1

№2
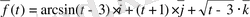
№3-7. Келесі вектор-функциялардың туындыларын табу керек.
№ 3
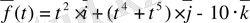
№ 4
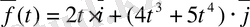
№ 5
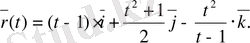
№ 6
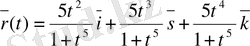
№ 7
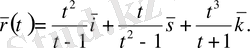
№8
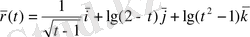 . Вектор-функцияның туындысын және анықталу облысын табу керек.
. Вектор-функцияның туындысын және анықталу облысын табу керек.
№9
 . Вектор-функцияның туындысын және анықталу облысын табу керек.
. Вектор-функцияның туындысын және анықталу облысын табу керек.
№10
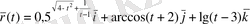 . Вектор-функцияның туындысын және анықталу облысын табу керек.
. Вектор-функцияның туындысын және анықталу облысын табу керек.
№11
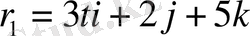 және
және
 вектор-функциялардың скаляр көбейтіндісінің туындысын табу керек.
вектор-функциялардың скаляр көбейтіндісінің туындысын табу керек.
№12
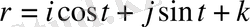 және
және
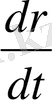 векторларының бір-біріне перпендикуляр екенін дәлелдеу керек.
векторларының бір-біріне перпендикуляр екенін дәлелдеу керек.
№13
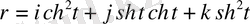 вектор-функциясының туындысын табу керек.
вектор-функциясының туындысын табу керек.
№14
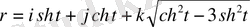 . Табу керек:
. Табу керек:

№15
 . Табу керек:
. Табу керек:
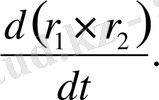
1. 2 Қисықтың әртүрлі берілу тәсілдері
Е
3
кеңістігіндегі қозғалушы М нүктесінің t
 I уақыт кезендегі орны координаталар басы О нүктесіне қарағанда ОМ=r(t) радиус-векторымен бір мәнді анықталады.
I уақыт кезендегі орны координаталар басы О нүктесіне қарағанда ОМ=r(t) радиус-векторымен бір мәнді анықталады.
I -сандық аралық (сегмент, интервал, жартылай интервал)
Қозғалыс кезінде r(t) радиус векторының бағыты да, шамасы да өзгереді.
Демек, t айнымалысы I аралығында өзгергенде r(t) радиус-векторы t скаляр аргументінің вектор функциясы болады.
(i, j, k) базисында әрбір t кезеніңде М нүктесінің координаталары x(t), y(t), z(t) болғандықтан
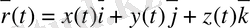 ) (1) арқылы анықталады.
) (1) арқылы анықталады.
(1) теңдігі - М нүктесінің (0, i, j, k) базисындағы қозғалыс заңы деп аталады.
Кеңістіктегі нүктелердің геометриялық орнын осы нүктенің траекториясы деп атайды. t
 I аралығында өзгергенде М нүктесі Е
3
кеңістігіндегі кейбір L-траекториясын сызады.
I аралығында өзгергенде М нүктесі Е
3
кеңістігіндегі кейбір L-траекториясын сызады.
Анықтама: Егер (1) векторлық теңдік t скаляр аргументті I аралығын М нүктесінің траекториясына гомеоморфты (өзара бір мәнді) бейнелесе, онда М нүктесінің траекториясын элементар қисық деп атайды.
Анықтама: Егер бейнелеу қайтымды, үзіліссіз және кері бейнелеу де үзіліссіз болса, онда f бейнелеу гомеоморфты деп аталады.
Е 3 кеңістігіндегі түзү, кесінді және сәуле қарапайым сызықтар деп аталады.
Анықтама: Осы сызықтардың кез келген біреуіне гомеморфты Е 3 кеңістігіне тиісті F фигурасы элементар қисық деп аталады.
Кесіндіге гомеоморфты фигура доға болады.
Ұштары Ажәне В нүктелері болатын жарты шеңбер немесе жарты эллипс АВ кесіндісіне гомеоморфты, яғни элементар қисық.
Енді элементар L қисығының О хуz координаталар жүйесіндегі теңдеуін анықтайық.
Тік бұрышты координаталар жүйесіндегі әрбір t
 Iсанына координаталары x(t), y(t), z(t) функциялары болатын М (х, у, z) нүктесі сәйкес келеді.
Iсанына координаталары x(t), y(t), z(t) функциялары болатын М (х, у, z) нүктесі сәйкес келеді.
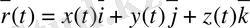 (2)
(2)
(2) - L сызығының векторлық теңдеуі.
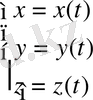 (3)
(3)
(3) теңдеуі кеңістіктік қисықтың параметрлік теңдеуі.
Анықтама: Саны шектеулі немесе саналымды жиын болатын элементар сызықтармен жабуға мүмкін болатын Е 3 кеңістігіне тиісті Ф фигурасы қисық деп аталады.
Анықтама: Егер х(t), y(t), z(t) функцияларының I аралығында к- ретке дейін үзіліссіз туындылары бар және бүкіл I аралығында
 болса, онда L қисығы к-класты тегіс қисық деп аталады.
болса, онда L қисығы к-класты тегіс қисық деп аталады.
Мысал: Параметр ретінде координаталар бас нүктесін және қисықтың кез келген нүктесі арқылы өтетін түзудің бұрыштық коэффициентін алып,
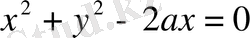 шеңберінің параметрлік теңдеуін құру керек.
шеңберінің параметрлік теңдеуін құру керек.
Шешуі: (сурет1. Шеңбердің параметрлік теңдеуін құру)
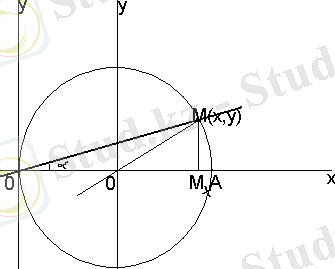
Сурет 1. Шеңбердің параметрлік теңдеуін құру.
 шеңбердің кез келген нүктесі болсын.
шеңбердің кез келген нүктесі болсын.
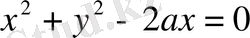 шеңберінің теңдеуін канондық түрге келтіреміз
шеңберінің теңдеуін канондық түрге келтіреміз
 .
.
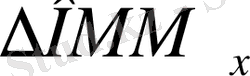 және
және
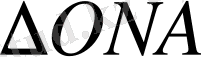 үшбұрыштары ұқсас. Ендеше осы үшбұрыштардың ұқсастық қатынастарын құрамыз:
үшбұрыштары ұқсас. Ендеше осы үшбұрыштардың ұқсастық қатынастарын құрамыз:
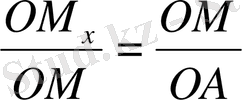 немесе
немесе
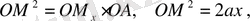 мұндағы
мұндағы

 үшбұрышынан:
үшбұрышынан:
 табамыз. Табылған теңдіктерді салыстырып, келесі теңдікті аламыз:
табамыз. Табылған теңдіктерді салыстырып, келесі теңдікті аламыз:

өйткені
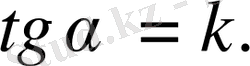
 шығатыны:
шығатыны:
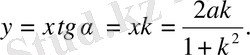
 шеңбердің параметрлік теңдеуі келесі түрде болады:
шеңбердің параметрлік теңдеуі келесі түрде болады:

Жауабы:
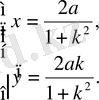
Өз бетімен шығаруға арналған есептер
№16 Жазықтықта берілген F
1
және F
2
(
 ) нүктелеріне дейінгі арақашықтықтардың көбейтіндісі
) нүктелеріне дейінгі арақашықтықтардың көбейтіндісі
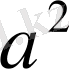 тұрақты шама болатындай барлық нүктелер жиынынан тұратын жазық фигураның теңдеуін құру керек (Кассини қисығы) .
тұрақты шама болатындай барлық нүктелер жиынынан тұратын жазық фигураның теңдеуін құру керек (Кассини қисығы) .
№17 Ұзындығы 2а-ға тең, диаметрі ОА болатын шеңбер берілген. А нүктесі арқылы шеңберге жанама жүргізілген. О нүктесі арқылы ОС сәулесі жүргізіліп, сол сәуленің бойында АВ жанама мен шеңбер арасында тұйықталған ВС кесіндісіне тең ОМ кесіндісі салынған. ОС сәулесін О нүктесі арқылы айналдырылған кезде М нүктесі Диоклес циссоидасы деп аталатын траектория сызады. Осы траекторияның теңдеуін құру керек.
№18 М нүктесі ОN түзуінің бойымен О нүктесін бірқалыпты айнала қозғалады. М нүктесінің траекториясының теңдеуін жазу керек (Архимед спиралі) .
№19 Ұзындығы 2а тұрақты шама болатын АВ кесіндісі өзінің ұштары арқылы
 тікбұрышты координаталар жүйесінің осьтерінің бойымен жылжиды. Координаталар бас нүктесінен АВ түзуіне ОМ перпендикуляр жүргізілген. Осындай М нүктелері арқылы құрылған фигураны жазу керек (төртжапырақты раушан гүл) .
тікбұрышты координаталар жүйесінің осьтерінің бойымен жылжиды. Координаталар бас нүктесінен АВ түзуіне ОМ перпендикуляр жүргізілген. Осындай М нүктелері арқылы құрылған фигураны жазу керек (төртжапырақты раушан гүл) .
№20 Радиусы а-ға тең щеңбердің қандай-да бір О нүктесі арқылы сәуле айналады. Осы сәуленің бойында А нүктесінің екі жағына да шеңбермен қиылысқанға дейін ұзындықтары 2b-ға тең АМ 1 және АМ 2 кесінділері салынады. Осы М 1 және М 2 нүктелері арқылы сызылған фигураның теңдеуін құру керек (Паскаль улиткасы, дербес жағдайда a=b болса, кардиоида) .
№21 Ұзындығы а-ға тең АВ кесіндісі өзінің ұштары арқылы тік бұрышты координаталар жүйесінің осьтері бойымен жылжиды. АС және ВС түзулері координаталар осьтеріне параллель және С нүктесінде қиылысады. С нүктесінен АВ түзуіне СМ перпендикуляр жүргізілген. Осындай М нүктелерінен тұратын траекторияның теңдеуін жазу керек (астроида) .
№22 Радиусы а-ға тең дөңгелек түзу бойымен жылжиды. Дөңгелектің центрінен d ара қашықтықта орналасқан және дөңгелекпен қатаң түрде байланған М нүктесінің траекториясының теңдеуін құру керек (мұндағы d=a болса -циклоида, d<a болса -қысқартылған циклоида, d>a болса - ұзартылған циклоида) .
1. 3 Қисыққа жүргізілген жанама және нормаль
Анықтама: Қиюшы түзудің шектік жағдайы қисыққа жүргізілген жанама деп аталады
Анықтама: Қ
исықтың M(t) нүктесі және оған шексіз жақын
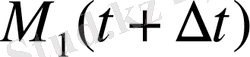 нүктелері арқылы өтетін қиюшының
нүктелері арқылы өтетін қиюшының
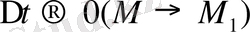 шектік жағдайы берілген нүктедегі
қисықтың жанамасы
деп аталады.
шектік жағдайы берілген нүктедегі
қисықтың жанамасы
деп аталады.
Теорема:
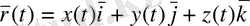 векторлық теңдеуімен берілген, Lтегіс қисықтың әрбір M нүктесінде осы M нүктесі және бағыттаушы
векторлық теңдеуімен берілген, Lтегіс қисықтың әрбір M нүктесінде осы M нүктесі және бағыттаушы
 векторымен анықталған T жанамасы бар болады
векторымен анықталған T жанамасы бар болады
Анықтама: Жазық қисықтың нормалі деп сол жазықтықта жататын, жанамаға перпендикуляр және жанасу нүктесі арқылы өтетін түзуді атайды.
Қисықтың әр түрлі берілу тәсілдеріндегі жанама мен нормальдың теңдеулері
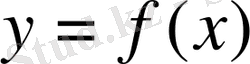
Айқын түрде
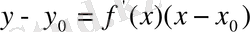
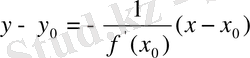
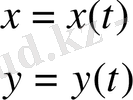
Параметрлік түрде

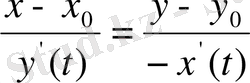
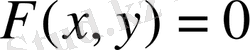
Айқын емес түрде
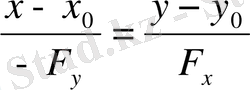
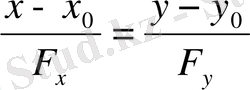
Мысалдар:
а)
 қисығына
А
(
қисығына
А
(
 ) және
В
(
) және
В
(
 ) нүктелерінде жүргізілген жанама және нормальдың теңдеулерін құру керек.
) нүктелерінде жүргізілген жанама және нормальдың теңдеулерін құру керек.
Шешуі: Қисық айқын түрде берілген, сондықтан есепті шешу үшін келесві формулаларды қолданамыз:
 - жанаманың теңдеуі,
- жанаманың теңдеуі,
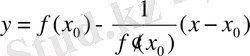 - нормальдың теңдеуі.
- нормальдың теңдеуі.
1)
А
(
 ) нүктесіндегі жанама мен нормальдың теңдеуін табамыз.
) нүктесіндегі жанама мен нормальдың теңдеуін табамыз.
 ;
;
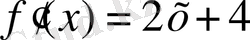 ,
,
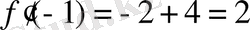 .
.
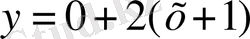 ,
,
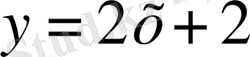 ;
;
 -
А
(
-
А
(
 ) нүктесіндегі жанаманың теңдеуі.
) нүктесіндегі жанаманың теңдеуі.
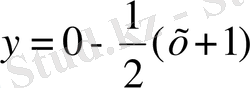 ;
;
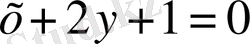 -
А
(
-
А
(
 ) нүктесіндегі нормальдың теңдеуі.
) нүктесіндегі нормальдың теңдеуі.
2)
В
(
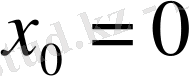 ) нүктесіндегі жанама мен нормальдың теңдеуін табамыз.
) нүктесіндегі жанама мен нормальдың теңдеуін табамыз.
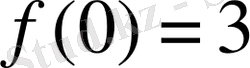 ;
;
 ;
;
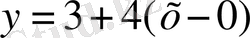 ,
,
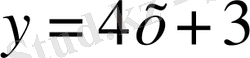 ,
,
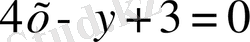 -
В
(
-
В
(
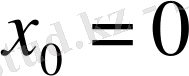 ) нүктесіндегі жанаманың теңдеуі.
) нүктесіндегі жанаманың теңдеуі.
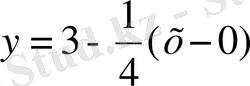 ;
;
 -
В
(
-
В
(
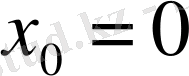 ) нүктесіндегі нормальдың теңдеуі.
) нүктесіндегі нормальдың теңдеуі.
Жауабы:
А
(
 ) нүктесіндегі
) нүктесіндегі
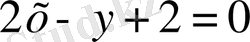 жанаманың теңдеуі,
жанаманың теңдеуі,
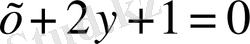 нормальдың теңдеуі;
В
(
нормальдың теңдеуі;
В
(
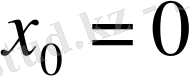 ) нүктесіндегі
) нүктесіндегі
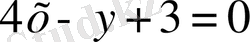 жанаманың теңдеуі,
жанаманың теңдеуі,
 нормальдың теңдеуі.
нормальдың теңдеуі.
ә)
 ,
,
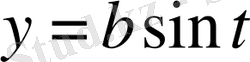 жүргізілген жанама және нормальдың теңдеулерін құру керек.
жүргізілген жанама және нормальдың теңдеулерін құру керек.
Шешуі : Қисық параметрлік түрде берілген, сондықтан жанама мен нормальдың теңдеулерін құру үшін келесі формулаларды қолданамыз:
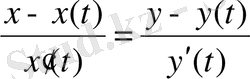 - жанаманың теңдеуі,
- жанаманың теңдеуі,
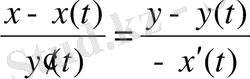 - нормальдың теңдеуі.
- нормальдың теңдеуі.
 ,
,
 .
.
Табылған мәндерді бірінші формулаға қойып, жанаманың теңдеуін аламыз:
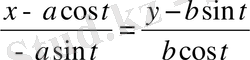 ;
;
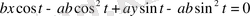 ;
;
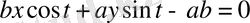 - жанаманың теңдеуі
.
- жанаманың теңдеуі
.
Табылған мәндерді екінші формулаға қойып, нормальдың теңдеуін аламыз:
 ;
;
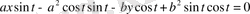 ;
;
 - нормальдың теңдеуі
.
- нормальдың теңдеуі
.
Жауабы:
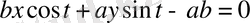 - жанаманың теңдеуі,
- жанаманың теңдеуі,
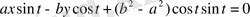 - нормальдың теңдеуі.
- нормальдың теңдеуі.
б)
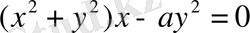 қисығына
А
(
қисығына
А
(
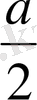 ,
,
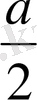 ) жүргізілген жанама және нормальдың теңдеулерін құру керек.
) жүргізілген жанама және нормальдың теңдеулерін құру керек.
Шешуі: Қисық айқын емес түрде берілген, сондықтан жанама мен нормальдың теңдеулерін құру үшін келесі формулаларды қолданамыз:
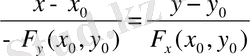 - жанаманың теңдеуі;
- жанаманың теңдеуі;
 - нормальдың теңдеуі.
- нормальдың теңдеуі.
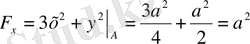 ;
;
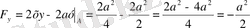 .
.
Табылған мәндерді бірінші формулаға қойып, жанаманың теңдеуін аламыз:
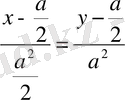 ;
;
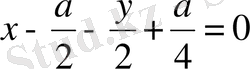 ;
;
 - жанаманың теңдеуі
.
- жанаманың теңдеуі
.
Табылған мәндерді екінші формулаға қойып, нормальдың теңдеуін аламыз:
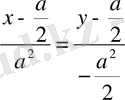 ;
;
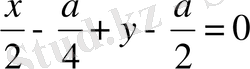 ;
;
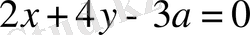 - нормальдың теңдеуі.
- нормальдың теңдеуі.
Жауабы:
Жанама
 , нормаль
, нормаль
 .
.
в)
 параболаға қай нүктеде жүргізілген жанама
Ох
осімен 45° бұрыш жасайды?
параболаға қай нүктеде жүргізілген жанама
Ох
осімен 45° бұрыш жасайды?
Шешуі:
Аналитикалық геометрии курсынан
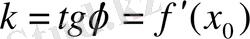 екені белгілі.
екені белгілі.
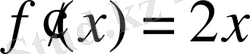

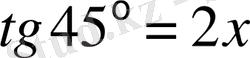 ;
;
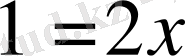 табамыз;
табамыз;
Осыдан
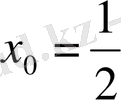 ,
,
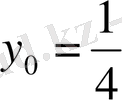 екендігі шығады.
екендігі шығады.
Жауабы:
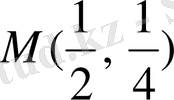 .
.
г)
Келесі қисықтардың қиылысу нүктелерін және олардың арасындағы бұрышын табу керек:
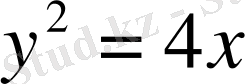 ,
,
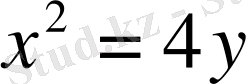 .
.
Шешуі: Алдымен берілген қисықтар үшін қиылысу нүтелерін табамыз. Ол үшін келесі теңдеулер жүйесін шешеміз:
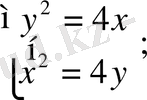
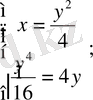
 ;
;

 .
.
Енді қисықтар арасындағы бұрышты табамыз:
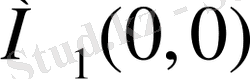 қиылысу нүктесі.
қиылысу нүктесі.
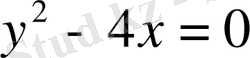 .
.
Қисық айқын емес түрде берілген, сондықтан жанаманың теңдеуін табу үшін келесі формуланы қолданамыз:
 ;
;
 ;
;
 .
.
Табылған мәндерді формулаға қоямыз:
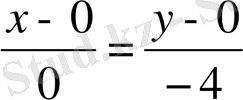 ;
;
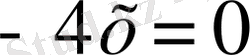 ;
;
 - бірінші қисық үшін жанаманың теңдеуі.
- бірінші қисық үшін жанаманың теңдеуі.
Енді екінші қисық үшін жанаманың теңдеуін табамыз:
 .
.
 ;
;
 .
.
Жанаманы табу үшін, табылған мәндерді формулаға қоямыз:
 ;
;
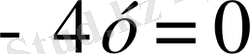 ;
;
 - екінші қисық үшін жанаманың теңдеуі.
- екінші қисық үшін жанаманың теңдеуі.
 және
және
 түзулері арасындағы бұрыш
түзулері арасындағы бұрыш
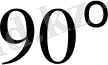 .
.
Енді екінші қиылысу нүктесіндегі қисықтар арасындағы бұрышты табамыз:
 .
.
 .
.
 ;
;
 ;
;
 - бірінші қисық үшін жанаманың теңдеуі.
- бірінші қисық үшін жанаманың теңдеуі.
Енді екінші қисық үшін жанаманың теңдеуін табамыз:
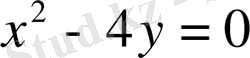 .
.
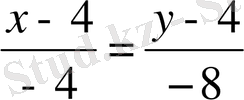 ;
;
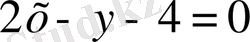 - екінші қисық үшін жанаманың теңдеуі.
- екінші қисық үшін жанаманың теңдеуі.
Екі қисық арасындағы бұрышты табу үшін, олардың жанамалары арасындағы бұрышты тапсақ, жеткілікті. Ол үшін келесі формуланы қолданамыз:
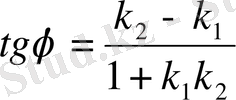 .
.
Жанамалардың бұрыштық коэффициенттерін табамыз:
 ,
,
 ,
,
 ;
;
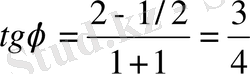 ;
;
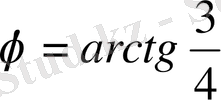
Жауабы:
 ,
,
 ;
;
 ,
,
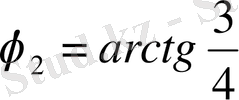 .
.
Өз бетімен шығаруға арналған есептер
№23-39 Келесі қисықтарға жүргізілген жанама және нормальдың тендеулерін құру керек:
№23
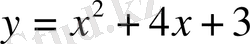 қисығына абсциссалары-1, 0, 1 нүктелерде.
қисығына абсциссалары-1, 0, 1 нүктелерде.
№24
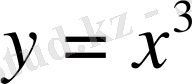 қисығына абсциссалары 0 және 1 нүктелерінде.
қисығына абсциссалары 0 және 1 нүктелерінде.
№25
 қисығына абсциссалары 0,
қисығына абсциссалары 0,
 ,
,
 нүктелерінде.
нүктелерінде.
№26
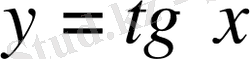 қисығына абсциссалары 0,
қисығына абсциссалары 0,
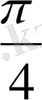 нүктелерінде.
нүктелерінде.
№27
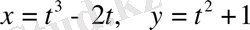 қисығына А(t=1) нүктесінде.
қисығына А(t=1) нүктесінде.
№28
 қисығына кез келген нүктеде.
қисығына кез келген нүктеде.
№29
 қисығына кез келген нүктеде.
қисығына кез келген нүктеде.
№30
 қисығына кез келген нүктеде.
қисығына кез келген нүктеде.
№31
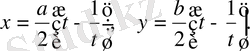 қисығына кез келген нүктеде.
қисығына кез келген нүктеде.
№32
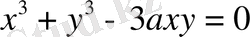 қисығына А(3а/2, 3а/2) нүктесінде.
қисығына А(3а/2, 3а/2) нүктесінде.
№33
 қисығына А(а/2, а/2) нүктесінде.
қисығына А(а/2, а/2) нүктесінде.
№34
 қисығына кез келген нүктеде
қисығына кез келген нүктеде
№35
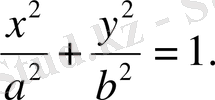
№36
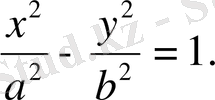
№37
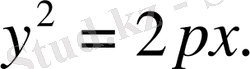
№38
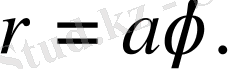
№39
 қисығына, А нүктесінде, мұндағы
қисығына, А нүктесінде, мұндағы
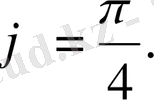
№40 Қай нүктеде
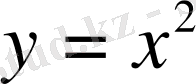 параболасына жүргізілген жанама Оx осімен 45
0
бұрыш жасайды?
параболасына жүргізілген жанама Оx осімен 45
0
бұрыш жасайды?
№41
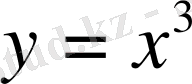 сызығына қандай да бір нүктеде жүргізілген жанама Ox осімен
сызығына қандай да бір нүктеде жүргізілген жанама Ox осімен
 -ке тең бұрыш жасауы мүмкін бе?
-ке тең бұрыш жасауы мүмкін бе?
№42
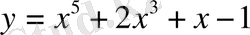 сызығына кез келген нүктеде жүргізілген жанаманың Ox осімен жасайтын көлбеулік бұрышы
сызығына кез келген нүктеде жүргізілген жанаманың Ox осімен жасайтын көлбеулік бұрышы
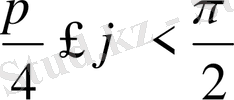 аралықта болатынын көрсету керек.
аралықта болатынын көрсету керек.
№43
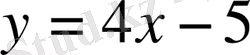 түзуіне параллель болатын,
түзуіне параллель болатын,
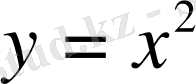 параболаға жүргізілген жанаманың теңдеуін табу керек.
параболаға жүргізілген жанаманың теңдеуін табу керек.
№44
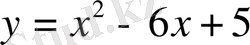 параболасына қай нүктеде жүргізілген жанама
параболасына қай нүктеде жүргізілген жанама
 түзуіне параллель болады?
түзуіне параллель болады?
№45
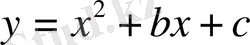 парабола теңдеуіндегі b және c тұрақтыларын x=2 нүктесінде
парабола теңдеуіндегі b және c тұрақтыларын x=2 нүктесінде
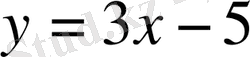 түзуге жанасатындай етіп таңдау керек.
түзуге жанасатындай етіп таңдау керек.
№46
 қисығының,
қисығының,
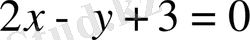 түзуіне параллель болатын жанамасын табу керек.
түзуіне параллель болатын жанамасын табу керек.
№47
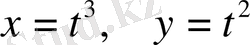 қисығына жүргізілген,
қисығына жүргізілген,
 нүктесі арқылы өтетін жанаманың теңдеуін табу керек.
нүктесі арқылы өтетін жанаманың теңдеуін табу керек.
№48-51 Келесі қисықтардың қиылысу нүктелерін және олардың арасындағы бұрыштарын табу керек:
№48

№49

№50
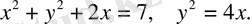
№51

№52-54 Келесі қисықтардың тік бұрыш жасап қиылысатынын дәлелдеу керек:
№52

№53
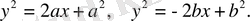
№54

1. 4 Ерекше нүктелер
Жазық қисықтың айқын емес түрде берілген теңдеуін қарастырайық.
F(x, y) = 0 - айқын емес түрде берілген қисықтың теңдеуі (1)
 қисықтың жанамасының теңдеуі (2)
қисықтың жанамасының теңдеуі (2)
(2) теңдігінің (
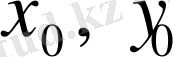 ) нүктесінде
) нүктесінде
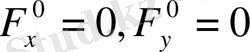 болса, бұл нүктеде (1) қисығының жанамасы анықталмайды. Осы нүкте айқын емес түрде берілген қисықтың ерекше нүктесі деп аталады.
болса, бұл нүктеде (1) қисығының жанамасы анықталмайды. Осы нүкте айқын емес түрде берілген қисықтың ерекше нүктесі деп аталады.
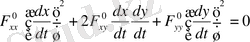 (3)
(3)
Егер (3) теңдігінің барлық коэффиценттері бір мезгілде нөлге тең болса, жанаманың бағыттаушы векторының координаталарының қатынасын алуға болады. (3) теңдігінің екі жағын да
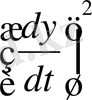 бөлеміз.
бөлеміз.
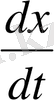 :
:
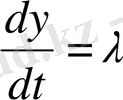 деп белгілейміз.
деп белгілейміз.
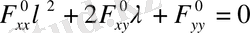 (4)
(4)
(4) - сипаттамалық теңдеу деп аталады.

δ - ның таңбасына қатысты квадрат теңдеудің шешімдерін қарастырамыз.
I δ > 0 (D < 0)
(4) теңдеуінің түбірлері жорамал сандар. Нақты түбірлері жоқ, яғни жанамалары жоқ. Бұл жағдайда ерекше нүкте оқшауланған деп аталады.
II δ < 0 (D > 0)
(4) теңдеуінің екі нақты және әр түрлі түбірлері бар. (
 ) нүктесінен қисықтың екі тармағы өтеді. Әрқайсысының жанамасының бағыты (3) арқылы анықталады. (
) нүктесінен қисықтың екі тармағы өтеді. Әрқайсысының жанамасының бағыты (3) арқылы анықталады. (
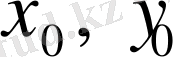 ) - буын немесе торапты нүкте деп аталады.
) - буын немесе торапты нүкте деп аталады.
III δ = 0 (D = 0)
(4) теңдеуінің бір - біріне тең екі түбірі бар. Бұл жерде бірнеше жағдайлар болуы мүмкін.
a) Оқшауланған нүкте.
б) I ретті қайту нүктесі. Қисық ерекше нүктеде ортақ жанамасы бар екі тармақтан тұрады. Бұл тармақтар осы нүктедегі жанаманың екі жағында, ал нормальдың бір жағында орналасқан.
в) II ретті қайту нүктесі. Бұл жағдайда қисықтың ерекше нүкте арқылы өтетін және ортақ жанамасы бар екі тармағы жанама мен нормальдың бір жағында орналасады.
г) Өзін - өзі жанайтын нүкте. Қисық ерекше нүктеде бірін - бірі жанайтын екі тармақтан тұрады.
д) Егер ерекше нүктеде
 болса, онда бұл нүкте арқылы қисықтың бірнеше тармақтары өтуі мүмкін.
болса, онда бұл нүкте арқылы қисықтың бірнеше тармақтары өтуі мүмкін.
Мысалдар:
а)
 қисығының ерекше нүктесін табу керек және ерекше нүктедегі жанаманың теңдеуін құру керек.
қисығының ерекше нүктесін табу керек және ерекше нүктедегі жанаманың теңдеуін құру керек.
Шешуі.
Берілген теңдеуді келесі түрде жазып аламыз
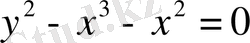 .
.
 және
және
 айнымалылары бойынша дербес бірінші туындыларын табамыз.
айнымалылары бойынша дербес бірінші туындыларын табамыз.
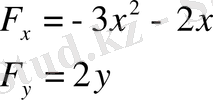 ,
,
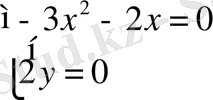 .
.
Осыдан
 , жүйенің екінші теңдеуін шешіп,
, жүйенің екінші теңдеуін шешіп,
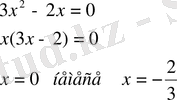 аламыз.
аламыз.
M 1 (-2/3; 0) - қисыққа тиісті емес.
Берілген қисық үшін
 ерекше нүктені таптық. Енді ерекше нүтенің түрін анықтау керек. Ол үшін
ерекше нүктені таптық. Енді ерекше нүтенің түрін анықтау керек. Ол үшін
 нүктесіндегі екінші дербес туындыларын табамыз .
нүктесіндегі екінші дербес туындыларын табамыз .
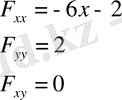
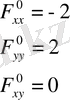 .
.
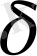 ның мәнін есептейміз,
ның мәнін есептейміз,
 ,
,
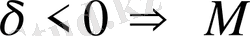 - ендеше торапты нүкте.
- ендеше торапты нүкте.
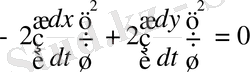 Келесі теңдеу бойынша жанамалардың бағытын анықтаймыз:
Келесі теңдеу бойынша жанамалардың бағытын анықтаймыз:
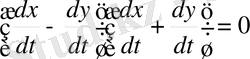

 x=y+C M нүктесінде 0=0+C C=0
x=y+C M нүктесінде 0=0+C C=0
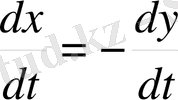 x =-y+C 0=0+C C=0
x =-y+C 0=0+C C=0
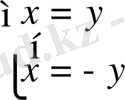 ерекше нүктедегі жанамалардың теңдеулері.
ерекше нүктедегі жанамалардың теңдеулері.
Жауабы : М(0, 0) - торапты нүкте.
ә)
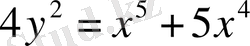 теңдеуімен берілген қисық үшін, ерекше нүктелерді табу керек.
теңдеуімен берілген қисық үшін, ерекше нүктелерді табу керек.
Шешуі.
Берілген теңдеуді келесі түрде жазып аламыз
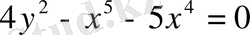 .
.
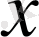 және
және
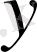 айнымалылары бойынша дербес бірінші туындыларын табамыз.
айнымалылары бойынша дербес бірінші туындыларын табамыз.
 .
.
Табылған өрнектерді жүйе түрінде жазып алып, оның шешімін табамыз.
 .
.
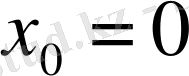
 нүктесі берілген қисық үшін ерекше нүкте болады (
нүктесі берілген қисық үшін ерекше нүкте болады (
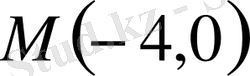 нүктесі қисыққа тиісті емес) . Ерекше нүктенің түрін анықтаймыз. Ол үшін
нүктесі қисыққа тиісті емес) . Ерекше нүктенің түрін анықтаймыз. Ол үшін
 нүктесіндегі екінші дербес туындыларын табамыз .
нүктесіндегі екінші дербес туындыларын табамыз .

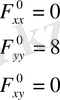 .
.
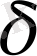 мәнін есептейміз.
мәнін есептейміз.
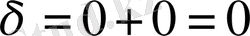 .
.
Бұл жерде бірнеше жағдайлар болуы мүмкін. Қисық ерекше нүктеде бірін - бірі жанайтын екі тармақтан тұрады. Ендеше М(0, 0) нүктесі өзін - өзі жанайтын нүкте.
Жауабы: М(0, 0) - өзін - өзі жанайтын нүкте.
б)
 (Никомед конхоидасы) қисығының ерекше нүктесін табу керек және ерекше нүктедегі жанаманың теңдеуін құру керек.
(Никомед конхоидасы) қисығының ерекше нүктесін табу керек және ерекше нүктедегі жанаманың теңдеуін құру керек.
Шешуі.
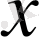 және
және
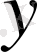 айнымалылары бойынша дербес бірінші туындыларын табамыз.
айнымалылары бойынша дербес бірінші туындыларын табамыз.

Табылған өрнектерді жүйе түрінде жазып алып, оның шешімін табамыз
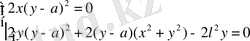 .
.
Бірінші теңдеуді шешіп,
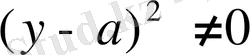 болғанда
болғанда
 екенін аламыз.
екенін аламыз.
Табылған шешімдерді бірінші теңдікке қойып, келесі өрнекті табамыз:
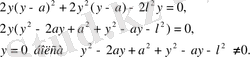
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz