Математика және күнтізбе

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Жангелдин ауданы, Милісай ауылы, « С. Мәуленов атындағы жалпы білім беретін мектебі» коммуналдық мемлекеттік мекемесі

Ғылыми жоба

Тақырыбы: Математика және күнтізбе

Бағыты: Экономикалық және әлеуметтік процестерді

математикалық модельдеу

Секция: математика

Оқушының аты жөні: Нағашыбай Ардақ

9 сынып оқушысы

Ғылыми жоба жетекшісі: Балдикова Анаргүл Бақытжанқызы

Математика пәнінің мұғалімі

Мазмұны

Кіріспе

Негізгі бөлім

1. 1. Күнтізбе және оның түрлері

2. Күнтізбедегі математикалық заңдылықтар

2. 1 Күнтізбедегі үшбұрыштар

2. 2 Күнтізбедегі төртбұрыштар

2. 3 Математикалық фокустар және күнтізбе

2. 4 Математикалық олимпиадалық есептер

Қорытынды

Пайдаланған әдебиеттер

$C:\Users\1\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20221101_215636.jpg$

Аннотация

"Математика және күнтізбе" тақырыбындағы математика бойынша зерттеу жобасында жұмыс жасау барысында автор кесте күнтізбелерінің ерекшеліктерін зерттей отырып, математика сабақтарын әртараптандыратын және сыныптан тыс жұмыстарда қолдануға болатын "күнтізбелер" тақырыбындағы көптеген тапсырмаларды зерттеуге болатындығы туралы гипотезаның шынайылығын дәлелдеу мақсатын қойды.

Математикадан ұсынылған "Математика және күнтізбе" жобасында автор күнтізбелер теориясын, күнтізбелердің түрлерін және олардың құрылу тарихын зерттеді, сонымен қатар күнтізбедегі үшбұрыштар мен төртбұрыштар сияқты математикалық заңдылықтарды қарастырды.

Математикадан " Математика және күнтізбе" тақырыбындағы осы зерттеу жұмысы жоба аясында күнтізбедегі математикалық трюктерді зерттеу бойынша практикалық зерттеу жүргізуге, сондай-ақ күнтізбені қолдана отырып математикадан олимпиадалық есептерді қарастыруға және шешуге мүмкіндік берді .

Аннотация

Работая над исследовательским проектом по математике на тему «Математика и календари», автор ставит своей целью доказать справедливость гипотезы о том, что, изучая особенности табличных календарей, можно изучить многие задачи по «календарям», которые разнообразят уроки математики и можно использовать во внеурочной деятельности.

В предложенном проекте «Математика и календарь» по математике автор изучил теорию календарей, виды календарей и историю их образования, а также такие математические законы, как треугольники и четырехугольники в календаре.

Данная научно-исследовательская работа по математике «Математика и календарь» позволила проекту провести практическое исследование по изучению математических трюков в календаре, а также рассмотреть и решить олимпийские задачи по математике с использованием календаря.

Annotation

Working on a research project in mathematics on the topic "Mathematics and Calendars", the author aims to prove the validity of the hypothesis that, by studying the features of tabular calendars, you can learn many tasks on "calendars" that diversify mathematics lessons and can be used in extracurricular activities .

In the proposed project "Mathematics and Calendar" in mathematics, the author studied the theory of calendars, the types of calendars and the history of their formation, as well as such mathematical laws as triangles and quadrangles in the calendar.

This research paper in mathematics "Math and Calendar" allowed the project to conduct a practical study on the study of mathematical tricks in the calendar, as well as to consider and solve Olympic problems in mathematics using the calendar.

Кіріспе

Біз күнтізбені қолдануға дағдыланғанбыз, тіпті біздің өмірімізде және бүкіл ойлауымызда уақыттың реттелген есебінің рөлі қаншалықты үлкен екенін білмейміз; бұл уақытта онсыз ешқандай мәдениеттің мүмкін еместігін көру қиын емес. (Н. И. Иделсон, кеңестік астроном-теоретик)

Біздің кез-келген адам аптаның қай күні, күні, айы, жылы екенін оңай айта алады. Әңгіме барысында біз уақыт тақырыбына әсер ететін бұрылыстарды жиі қолданамыз:" бір аптадан кейін", " бір жыл бұрын", " жаңа дәуірге дейін " және т. б. ? Қазіргі уақытта күнтізбенің не екенін білмейтін адам жоқ. Біз оның қызметтеріне күн сайын жүгінеміз. Күнтізбе бізге таныс және қажетті тақырыпқа айналды. Біз күнтізбені қолдануға дағдыланғанбыз, сондықтан біз қазіргі қоғамды уақыттың реттелген есебінсіз елестете алмаймыз.

Белгілі бір жолмен жүйеленген он екі сандық кесте ғалымдарға ғана емес, математиканы сүйетіндерге де қызықты. Сонымен, математикалық есептердің көптеген жинақтарында, әртүрлі математикалық жарыстардың, конкурстар мен олимпиадалардың есептерінде күнтізбеге байланысты есептер бар.

Осыған сүйене отырып, сұрақ туындайды: "күнтізбеде қандай ерекшеліктер мен заңдылықтар бар?».

Зерттеудің өзектілігі : Қабырға күнтізбесімен біз күн сайын кездесеміз. Бұл біз үшін таныс және қажет нәрсе. Біз геометрия сабағында мұғалім ұсынған мәселені шешкеннен кейін, "тікбұрышты үшбұрыштар" тақырыбын зерттеген кезде қабырға күнтізбесіне қызығушылық таныттық: "егер сіз 10, 20 сандарын және 30 жылдың 2019 қаңтарын қоссаңыз, сіз изоссельдер үшбұрышын аласыз.

Мұны дәлелдеңіз. Күнтізбе мен үшбұрыштар туралы міндет үшбұрыштардың теңдігі белгілері үшін стандартты емес міндет болды және көптеген студенттер арасында қызығушылық пен көптеген сұрақтар тудырды. Мұғалімнің кеңесі бойынша біз тапсырмаларды зерттеуді жалғастырып, туындаған сұрақтарға жауап бердік. Біздің зерттеуіміздің нәтижесі "Математика және күнтізбе " жобасы болды. Біз жауап алғымыз келетін сұрақтар:

Егер сіз кез-келген жылы 10, 20 және 30 Қаңтарда сандарды қоссаңыз, сіз изоссельдер үшбұрышына ие бола аласыз ба? Егер біз бір жылдың кез келген айының 10, 20 және 30 сандарын қоссақ, нәтиже қандай болады?

Егер біз кез-келген айда басқа сандарды қоссақ, изоссельдер үшбұрышы пайда бола ма? Зерттеу тақырыбын анықтау. Күнтізбе мен үшбұрыштар туралы есепті зерттей отырып, олар сұрақ қойды: математикалық әдебиетте "күнтізбелер"тақырыбында әлі де есептер бар ма? Интернет-ресурстардан күнтізбенің тарихы, күнтізбелердің түрлері туралы ғана білдік, бірақ бізге осы тақырып бойынша міндеттер ғана қажет болды.

Жетекші "Математика" газетімен жұмыс істеуге кеңес берді, онда олимпиадалардың, әртүрлі математикалық жарыстардың, конкурстардың және кейбір математикалық жинақтардың тапсырмалары жиі басылады. Мұндай тапсырмалар әртүрлі деңгейдегі олимпиадаларда жиі кездесетіні белгілі болды.

Мұндай мәселелерді шешу үшін күнтізбенің кейбір ерекшеліктерін білу керек. Мәселені тұжырымдау 1. Математика сабақтарында қабырға күнтізбесін қолдануға бола ма? Ол үшін математика әдебиетінде сабақтарда, олимпиадаларда және әртүрлі математикалық турнирлерде ұсынуға болатын "күнтізбелер" тақырыбындағы тапсырмалар бар-жоғын білу керек. Кесте күнтізбелерінің қандай ерекшеліктері бар?

Зерттеу гипотезасы :кесте күнтізбелерінің ерекшеліктерін зерттей отырып, математика сабақтарын безендіретін "күнтізбелер" тақырыбындағы көптеген мәселелерді зерттеуге болады және оларды сыныптан тыс жұмыстарда қолдануға болады: олимпиадалар, турнирлер, конкурстар, марафондар және т. б. жобаның мақсаты: гипотезаның шынайылығын дәлелдеу.

Осыған сүйене отырып, сұрақ туындайды: "күнтізбеде қандай ерекшеліктер мен заңдылықтар бар?».

Жұмыстың мақсаты : күнтізбедегі математикалық заңдылықтарды зерттеу және жүйелеу.

Міндеттері:

* "Күнтізбе"ұғымын сипаттайтын жаратылыстану және көркем әдебиетті оқып, талдаңыз. Әдебиетпен жұмыс істеуді үйрену. Интернеттен ақпарат табыңыз.

* Өз ой-өрісін кеңейту, жаңа білім мен дағдыларды алу.

* Математика әуесқойлары үшін" күнтізбе " ұғымы туралы ақпаратты қорытындылау және жүйелеу.

Зерттеу жұмысымды бастамас бұрын сауалнама жүргіздім. Сауалнама нәтижесі төмендегідей:

1) Күнтізбе өмірде қажет па?

а) Иә-85, % б) жоқ-15%

2) Күнтізбенің түрлерін білесіз ба?

а) иә-33%, жоқ-67%

3) Күнтізбе мен математиканың арасында байланыс бар ма?

а) иә-48%, жоқ -52%

4) Күнтізбеде математикалық заңдылықтарды кездестіруге бола ма?

а) иә- 35, жоқ-65%

5) Күнтізбе арқылы математикалық фокустардың сырын ашуға бола ма?

а) иә-42%, б) жоқ-58%

1. 1 Күнтізбе және оның түрлері

Күнтізбелердің түрлері

Күнтізбе-күн мен түннің өзгеруі, ай фазаларының өзгеруі, жыл мезгілдерінің өзгеруі сияқты табиғат құбылыстарының жиілігіне негізделген ұзақ уақыт аралықтарын санау жүйесі.

"Күнтізбе" сөзі латын calendae сөзінен шыққан - Ежелгі Римде әр айдың алғашқы күндері (күнтізбелер) осылай аталған. Өз кезегінде, бұл зат есім Калео - "жариялау", "шақыру"архаикалық етістігінен шыққан. Бұл Римде айдың басы әрқашан ерекше діни қызметкерлер салтанатты түрде жарияланғанына байланысты.

Содан кейін calendarium сөзі пайда болды, ол "қарыз кітабы"дегенді білдіреді. Ежелгі Римде борышкерлер айдың алғашқы күндерінде, яғни күнтізбелерде пайыздар төледі. Қазіргі мағынада күнтізбе-бұл аспан денелерінің көрінетін қозғалыстарының жиілігіне негізделген жылды ыңғайлы мерзімді уақыт аралықтарына бөлу тәсілі.

Күнтізбенің негізгі міндеттері-уақыт аралықтарын белгілеу және өзгерту. Егер жыл күннің бүтін санынан тұрса, сіз нақты күнтізбені жасай аласыз. Сондықтан нақты күнтізбені жасау мүмкін емес! Дәл және ыңғайлы күнтізбені жасауға тырысулар бар, сондықтан бірнеше күнтізбелер бар, мысалы,

* Ай күнтізбесі;

• Солнечный календарь;

* Күн-ай күнтізбесі;

* Джулиан күнтізбесі ("ескі стиль") ;

Григориан күнтізбесі ("жаңа стиль") және т. б.

Сонымен, ай күнтізбесі 29 немесе 30 күнге созылатын ай Айына негізделген. Күн жылының ұзақтығы ескерілмейді. Ай күнтізбесіндегі жылдың ұзындығы-354 күн. Көптеген мұсылман елдері ай күнтізбесін біздің уақытқа дейін қолданады.

Ауылшаруашылық жұмыстары мен әлеуметтік өмірді күнтізбеге сәйкестендіру үшін он үшінші ай мезгіл-мезгіл ай күнтізбесінің қысқа жылына қосыла бастады. Бұл жағдайда жиі шатасулар болды. Күн-ай күнтізбесі ежелгі Египетте құрылды.

Онда 12 күн 30 ай болды және жыл соңында тағы 5 күн қосылды. Кейінірек Эвергет 4 жылда бір рет 366-шы күнді қосуды ұсынды. Қазіргі уақытта бұл күнтізбе Эфиопияда қолданылады.

Сондай-ақ, "жаңа стиль" және "ескі стиль"күнтізбелері бар. Мұндай күнтізбелер-Григориан күнтізбесі және Джулиан күнтізбесі. Юлий Цезарь кейбір жылдарды 365 күн, басқаларын 366 күн деп санауға шешім қабылдады, оларды кезектестірді: үш қысқа, төртінші ұзақ.

Барлық тақ айларда 31 күн, тіпті 30 күн болды, ақпаннан басқа, 29 күн, ал 30-ы тек жаңа жыл болды. Мұндай күнтізбедегі жылдың ұзақтығы 365 күн және 6 сағат болды. Бұл күнтізбе Джулиан күнтізбесі деп аталды. Бірақ бұл күнтізбе астрономиялық жылдан 11 минут 14 секундқа асып түсті. 325 жылға қарай асып кету 3 күн болды. Содан кейін күнтізбенің жаңа реформасын құру туралы шешім қабылданды.

Реформаның бастамашысы Рим папасы Григорий 13 болды және оны итальяндық дәрігер, математик және астроном Алиозий Лилио жасаған. Мұндай күнтізбеде сандар 10 күнге жылжып, қарапайым және секіріс жылдарының ауысуын қалдырды. Егер жыл 2 нөлмен аяқталса және оның жүздеген саны 4-ке бөлінбесе, онда бұл жыл қарапайым емес, секіргіш емес. Бұл күнтізбе Григориан деп аталады.

Ресей, Еуропа, АҚШ тұрғындары және басқалары григориан күнтізбесін қолданады. Өзінің бүкіл тарихында "күнтізбе" сөзінің мағынасы бірнеше рет өзгерді. Бірақ кез-келген жаңа мағына уақыт ұғымымен және оны өлшеу проблемасымен байланысты болды.

Бір қызығы, әлемдегі алғашқы күнтізбе біздің заманымызға дейінгі үш мыңыншы жылы, Еуропада, әйгілі Stonehenge (Stonehenge) қаласында пайда болды, ол өзі күнтізбенің бір түрі. Бірақ сол күндері, әрине, уақыт мәселесі қазіргі әлемдегі сияқты өзекті емес еді. Содан кейін күнтізбе айналадағы шындықты білу әдісі, жердегі болмыстың заңдылықтарын түсінуге және түсінуге тырысу болды.

2 Күнтізбедегі математикалық заңдылықтар

2. 1 Күнтізбедегі үшбұрыштар

Есеп . Егер сіз 2019 жылдың күнтізбесінде 10, 20 және 30 қаңтар сандарын қоссаңыз, сіз изоссельдер үшбұрышын аласыз.

Шешімі.

Мәселені шешудің ыңғайлылығы үшін біз күнтізбені қолданамыз, онда сандарды қағазға жазамыз.

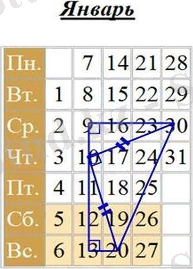
календарь календарь 2

Сонымен, бұл мәселені бекітуге қайта құруға болады: 2019 жылғы күнтізбеде 10, 20 және 30 қаңтар сандарын қосқанда, изоссельдер тікбұрышты үшбұрыш алынады.

Қорытынд ы. Күнтізбелердің келесі ерекшелігі бар: егер кез-келген жылдың күнтізбесінде 10, 20 және 30 қаңтарға сәйкес келетін сандарды қоссаңыз, онда сіз 10, 20 және 30 сандары бар жасушалардың орталықтары бір сызықта орналасқан жағдайларды қоспағанда, изоссельдер үшбұрышын аласыз.

2. 2 Күнтізбедегі төртбұрыштар

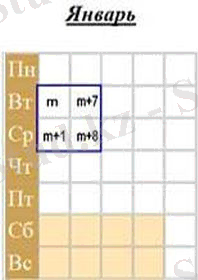
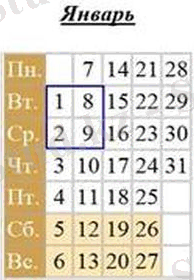
календарь 3 календарь 4

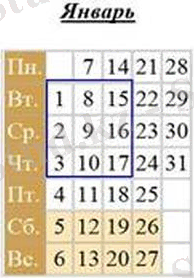
календарь 5

Кез-келген айда төрт саннан (2х2), тоғыз саннан (3х3) және Он алты саннан (4х4) тұратын квадраттарды бөлуге болатындығын ескеріңіз.

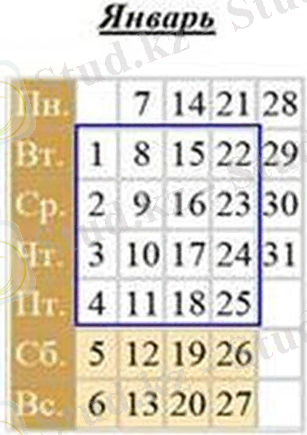
Сол сияқты, 2019 жылғы күнтізбені, қаңтар айын қарастырыңыз.

Мұндай квадраттардың қандай қасиеттері бар?

1) 2х2 шаршы

Есеп 1. Таңдалған квадраттың бір диагоналіндегі сандардың қосындысы басқа диагональдағы сандардың қосындысына тең.

Бірінші таңдалған ең кіші Сан m болсын, күнтізбедегі сандардың орналасуына сүйене отырып, басқа сандар m + 1, m + 7 және m + 8 болады.

Шаршының бір диагоналінің қосындысы: m +(m + 8) = 2M + 8.

Басқа диагональдың қосындысы: (m + 1) + (m + 7) = 2M + 8.

Осылайша, өрнектер тең, ал квадраттың бір диагоналіндегі сандар екінші диагональдағы сандардың қосындысына тең.

Есеп 2. Бөлінген квадраттағы төрт санның қосындысын табу үшін бір диагональдағы сандардың қосындысын екі есе көбейту жеткілікті.

Есеп алдыңғы дәлелден айқын көрінеді.

Мысал: 2(1 + 8) = 20.

2) 3х3 шаршы

Қасиет 1 . Күнтізбенің таңдалған квадратында тоғыз санның қосындысын табу үшін кіші санға 8 қосып, қосындыны 9-ға көбейту керек.

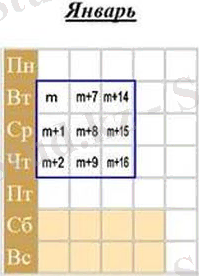
календарь 7

Бірінші таңдалған ең кіші Сан m болсын, күнтізбедегі сандардың орнына сүйене отырып, басқа сандар M + 1, m + 2, m + 7, m + 8, m + 9, m + 14, m + 15 және m + 16 болады.

Сандарды қосу арқылы біз 9M + 72 = 9(m + 8) аламыз.

Демек, сандардың сомасы осындай квадраттар таба, егер таңдап алады қатарына қосуы 8 сомасын көбейту 9.

Мысал: (1 + 8) 9 = 81.

Қасиет 2. Күнтізбенің таңдалған квадратында тоғыз санның қосындысын табу үшін үлкен саннан 8 санын алып тастап, айырмашылықты 9-ға көбейту керек.

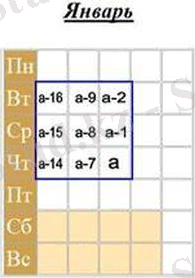
календарь 8

Соңғы бөлінген ең үлкен Сан күнтізбедегі сандардың орналасуына сүйене отырып, басқа сандар тең болсын, а - 1, а - 2, А - 7, а - 8, А - 9, а - 14, а - 15 және а - 16.

Сандарды қосу арқылы біз аламыз: 9а - 72 = 9(a-8) . Демек, сандардың сомасы осындай квадраттар таба, егер үлкен санын шегеруге 8 және айырымы-ге көбейту 9.

Мысал: (17 - 8) 9 = 81.

3) 4х4 шаршы

Қасиет 1. Күнтізбенің таңдалған квадратында он алты санның қосындысын табу үшін үлкен саннан 12 санын алып тастап, алынған айырмашылықты 16-ға көбейту керек.

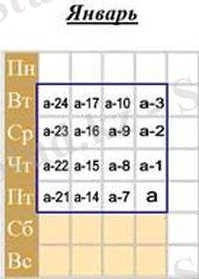
календарь 9

Соңғы бөлінген ең үлкен Сан күнтізбедегі сандардың жағдайына сүйене отырып, басқа сандар А - 1, а - 2, а - 3, А - 7, а - 8, А - 9, а - 10, а - 14, а - 15, а - 16, а - 17, а - 21, а - 22, а - 23 және а - 24 тең болсын.

Сандарды қосу арқылы біз аламыз: 16а - 192 = 16(a-12) . Сонымен, мұндай квадраттардың сандарының қосындысын үлкен саннан 12 алып тастап, айырмашылықты 16-ға көбейту арқылы табуға болады.

Мысал: (25 - 12) 16 = 208.

2. 3 Күнтізбедегі математика

Күнтізбені зерттеу барысында алынған заңдылықтар негізінде "жылдам есептеулердің"бірнеше трюктері жасалады.

Математикалық трюктер және күнтізбе

1. Фокус-болжау. Бұл фокуста сиқыршы өзінің дарынын көрсете алады және бірнеше сандарды тез қосуды біледі. Көрерменді кез-келген айда жұмыс үстеліндегі күнтізбеге 16 санның кез-келген квадратына айналдыруды сұраңыз.

Оған жылдам қарап, сіз параққа болжам жазып, оны конвертке салып, көрерменге сақтайсыз. Содан кейін көрерменнен осы күнтізбедегі кез-келген санды таңдап, оны шеңберге айналдырып, сол жолдағы және сол бағандағы барлық сандарды жаңа ғана дөңгелектелген санмен қиып алуды сұраңыз.

Екінші сан ретінде көрермен сызылмай қалған кез-келген санды айналдыра алады. Осыдан кейін ол үшінші санды кесіп тастауы керек, ал тиісті жолдар мен бағандар сызылады.

Финалда сіз конверттен парақты алуды тиімді түрде ұсынасыз және оған осы сандардың алдын-ала жазылғанына көз жеткізесіз.

Мұны істеу үшін сізге шаршының екі диагональды қарама-қарсы бұрыштарында орналасқан екі санды қосып, табылған соманы екі есе көбейту керек болды.

2. Қосындыны табу фокусы . Бұл фокуста сиқыршы күнтізбедегі дөңгелек шаршыға кіретін сандардың қосындысын тез болжай алады. Мұны істеу үшін көрерменді кез-келген айда қабырға күнтізбесінде 16 саннан тұратын шаршыға айналдыруды сұраңыз. Оған жылдам қарап, қажетті есептеулерді жасай отырып, осы шаршыға түскен барлық сандардың қосындысын атаңыз.

Мұны істеу үшін кез-келген диагоналдың қарама-қарсы ұштарында тұрған екі санның қосындысын квадраттың шеңберіне 8-ге көбейту керек болды.

3. Жұмулы көзбен есептеу . Бұл жолы біз күнтізбеге мүлдем қарамаймыз. Көрерменнен қабырға күнтізбесінде кез-келген айды таңдап, оған 9 саннан тұратын шаршыны дөңгелектеуін сұраңыз. Осы шаршыға түскен сандардың ең кішісін атаңыз. Бірнеше минуттан кейін осы 9 санның қосындысын атаңыз.

Мұны істеу үшін Сіз аталған санға 8 қосып, нәтижені 9-ға көбейтуіңіз керек.

2. 4. Математикалық олимпиадалық есептер

1. Бір айда 5 дүйсенбі және 5 бейсенбі болуы мүмкін бе? Негіздеңіз бар.

Жауабы: Егер ай 31 күн болса және ол дүйсенбіден басталса, онда ол 5 дүйсенбі, 5 сейсенбі және 5 сәрсенбі болуы мүмкін, бірақ аптаның қалған күндері төрт, өйткені 5+5+5+4+4+4+4=31. Жауап: мүмкін емес.

2. 2004 жылдың ақпан айында 5 жексенбі, барлығы 29 күн. Аптаның қай күні 2004 жылдың 23 ақпанына келеді?

Жауабы: Егер ақпан айында 29 күн және 5 жексенбі болса, онда бірінші қайта тірілу 1 ақпан болады. Осыдан 23 ақпан - дүйсенбі.

3. Бір айда үш жұма жұп сандарға түсті. Аптаның қай күні осы айдың 15-і болды?

Жауабы: Айдың жұп күндеріне келетін үш жұма тек 2, 16 және 30 болуы мүмкін. 15-ші күн бейсенбі болды.

4. Белгілі. 1 желтоқсан сәрсенбіге келеді. Аптаның қай күні келесі жылдың 1 қаңтарына келеді?

Жауабы: Сәрсенбі 1, 8, 15, 22 және 29 желтоқсан, бейсенбі 30, жұма 31. Жауап: келесі жылдың 1 қаңтары сенбі.

5. Кейбір айда үш жексенбі жұп сандарға түсті. Осы айдың 20 күні аптаның қай күні болды?

Жауабы: Тіпті жексенбі 2, 16, 28. Демек, осы айдың 20 күні - бейсенбі.

6. Бір жылда қайта тірілудің ең көп саны қандай болуы мүмкін? Жауабы: 53 жексенбі.

7. Жылына бес жексенбілік айдың ең көп саны қандай болуы мүмкін?

Жауабы: 5 ай. Қалыпты жыл жексенбіден, ал сенбі немесе жексенбіден басталуы керек.

8. Бір жылы бір айдың кейбір күндері жексенбі болған жоқ. Бұл сан қандай болуы мүмкін?

Жауабы: 31-ші сан және тек біреуі. Мысалы, 2007 жылы бірде-бір жексенбі 31 Сан болған жоқ.

9. Кейбір айда үш сенбі жұп сандарға түсті. Аптаның қай күні осы айдың 28-і болды?

Жауабы: Алғашқы" жұп " сенбі х(х - жұп сан) арқылы көрсетілген санға түссін. Келесі жұп сенбі екі аптадан кейін болады, яғни. (X+14) -ші, ал үшінші "жұп" сенбі - (x+28) -ші. Бірақ бір айда 31 күннен аспайды, сондықтан x+28≤ 31. Бұл теңсіздіктің бір жұп шешімі бар х=2. Содан кейін үшінші" жұп " сенбі 30-да, ал 28-де бейсенбі болды.

10. Бір айда үш жұма жұп сандарға түсті. Аптаның қай күні осы айдың 15-і болды?

11. Кейбір айда үш жексенбі жұп сандарға түсті. Осы айдың 20 күні аптаның қай күні болды?

12. 2010 жылдың бірінші және соңғы күні аптаның сол күні екенін дәлелдеңіз.

Жауабы: 2010 жыл кібісе емес 2. Қалыпты жыл 365=52x7+1 күнді, яғни 52 толық аптаны және бір күнді қамтиды. Сондықтан кез-келген қалыпты жыл аптаның сол күні басталып, аяқталады. 2010 үшін бұл жұма болады.

13. Кейбір айда дүйсенбі сейсенбіден гөрі көп, ал жексенбі сенбіден көп. Аптаның қай күні осы айдың 5-ші күні болды? Бұл ай желтоқсан болуы мүмкін бе?

Жауабы: 4 апта ішінде, 1-ден 28-ге дейін, аптаның әр күні дәл 4 рет кездеседі, сондықтан жағдай 29 - жексенбі, 30-дүйсенбі, ал 31 - ші күні осы айда болмайды. Демек, ай жексенбіден басталды, ал оның 5-ші күні бейсенбі болды. Бұл ай желтоқсан бола алмады: Желтоқсанда 31 күн.

14. Бір жыл қатарынан үш ай тек төрт жексенбіден тұрды. Осы айлардың бірі ақпан екенін дәлелдеңіз.

Жауабы: Егер ақпан көрсетілген "қатарынан үш айға" кірмесе, онда күндер саны - 91 немесе 92. Бірақ 91 = 7x13, 92=7x13+1, яғни бұл жағдайда үш айда 13 толық апта болады, яғни аптаның әр күні, соның ішінде жексенбі, 13 рет болады және шарт орындалмайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.