Өнімділік әдістерін салыстыру

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Кіріспе

Тақырыптың өзектілігі: Python - әр түрлі типтегі қосымшаларды жасауға арналған танымал жоғары деңгейлі бағдарламалау тілі. Python машиналық оқыту және жасанды интеллект зерттеу саласында кеңінен таралған. Python - жоғары дәрежелі кодтың оқылуын және әзірлеушінің өнімділігін арттыруға мақсатталған жалпы мақсаттағы бағдарламалау тілі. Python тілі аз синтаксисті талап етеді. Бірақ сол уақытта стандартты кітапханасы үлкен көлемді пайдалы функцияларды қамтиды.

Сызықты емес алгебралық және трансценденттік теңдеулер жүйесінің түбірлерін анықтау үшін тура әдістер емес, тек итерациялық әдістер ғана қолданылады. Көбінесе сызықты емес алгебралық және трансценденттік теңдеулер жүйесін шешу үшін Ньютон әдісі мен оның түрлендірулері және жартылай бөлу әдісі қолданылады.

Курстық жұмыстың мақсаты: Сызықтық емес теңдеулерді жартылай бөлу әдісімен және Ньютон әдісімен шешуге арналған бағдарлама жазу. Өнімділік әдістерін салыстыру.

Курстық жұмыстың міндеттері:

Ньютон (жанама) әдісімен шығару ;
жартылай бөлу әдісімен шығару;
Ньютон (жанама) әдісімен және жартылай бөлу әдісімен шығарылған есепті салыстыру;
қайсы тәсіл тиімді екенін анықтау.

1. Тапсырма қойылымы

1. 1 Сызықтық емес теңдеулер

Сызықтық емес теңдеулерді 2 классқа бөлуге болады - алгебралық және трансценденттік.

Алгебралық теңдеу деп - тек алгебралық функцияларды қамтитын

теңдеуді айтады (бүтін, рационалдық, иррационалдық) . Көпмүшелік жиі бүтін алгебралық функция болып келеді. Басқа функцияларды қамтитын теңдеу (тригонометриялық, көрсетімділік, логарифмдік және басқалары)

трансцендентті деп аталады.

Сызықтық емес теңдеулерді шешу әдістері екі топқа бөлінеді:

1. дәл әдістер;

2. итерационды әдістер.

Дәл әдістер түбірлерді кейбір соңғы қатынастар(формулалар) түрінде

жазуға мүмкіндік береді. Алгебраның мектеп курсынан тригонометриялық,

логарифмдік, көрсетімдік және жай алгебралық теңдеулерді шешудің мыныдай әдістері белгілі.

f (x) функциясын нөлге ауыстыратын кез-келген ξ мағынасын, яғни:

f (ξ) = 0 (1. 1)

(1. 1) теңдеудің түбірі немесе f (x) функциясының нөлі деп аталады.

f (x) = 0 теңдеуінің түбірін итерациондық әдісімен табу есебі 2 буыннан тұрады:

1- түбірлердің бөлінуі - түбірдің жуықтаудалған мәнін немесе оның құрамындағы кескіндерді іздеу;

2 - жуықтаудалған түбірлерді анықтау - оларды берілген нақтылықтың дәрежесіне жеткізу.

Түбірлерді бөлу процессі f (x) функциясын x = a және x = b облысының шекаралық нүктелерінде белгілерді орнатумен басталады.

Бір белгісізімен болған кез-келген теңдеу мынандай түрде жазылуы

мүмкін:

f (x) = 0, (1. 3)

мұндағы f (x) - полиномиальды немесе трансцендентті функция, кейбір шекті

немесе шексіз (а, b) интервалында анықталған.

f (x) функциясын нөлге айналдыратын кез-келген ξ мәні, яғни f (ξ) = 0, шешімі немесе теңдеудің түбірі деп, немесе у = f (x) функциясының нөлі деп аталады .

Теңдеулердің нақты түбірлерін шығару әдетте үш кезеңнен құралады:

1. (1. 3) теңдеуінің барлық түбірлері орналасқан облыстың шектерінің анықтамасы;

2. түбірлердің бөлінуі, яғни теңдеудің бір тек қана бір түбірі орналасқан [a _k , b _k ], аз уақыт аралығының орнату мүмкіндігі, мұндай теңдеулер шектелген деп аталады;

3. түбірлерді анықтау, яғни берілген анықтау дәрежесімен шешу. [a, b] кесіндісіне жататын (1. 3) теңдеуінің түбірін табу үшін, бұл кескінді қаққа бөлеміз. Егер $f\left( \frac{a + b}{2} \right) \$ = 0, онда $x$ = $\frac{a + b}{2}$ (1. 3) теңдеудің түбірі болып келеді. Егер $f$ ( $\frac{a + b}{2}$ ) = 0 -ге тең емес болса, онда f (x) функциясының соңында қарама-қарсы белгісі бар, [a, $\frac{a + b}{2}$ ] немесе [ $\frac{a + b}{2}, b$ ] жартысын таңдаймыз. Жаңа кескінді [a ₁ , b ₁ ] тағы да қаққа бөліп, осы іс-әрекеттерді қайталаймыз. Жартылай бөлу әдісі теңдеуді дөрекі табу үшін қолдануға қолайлы, әдіс қарапайым және сенімді, әрқашан келіседі. [1]

1. 2 Ньютон (жанамалар) әдісі

"Ньютон әдісі" атауы Исаак Ньютонның әдістің ерекше жағдайын сипаттауынан шыққан DE analysi per aequationes numero terminorum infinitas (1669 жылы жазылған, 1711 жылы Уильям Джонс жариялаған) және DE metodis fluxionum et serierum infinitarum (1671 жылы жазылған, аударылған және әдіс ретінде жарияланған шексіз Сан) . 1736 жылы Джон Колсон Флюксии) . Дегенмен, оның әдісі жоғарыдағы заманауи әдіспен айтарлықтай ерекшеленеді. Ньютон бұл әдісті тек көпмүшелерге қолданды, түбірді бастапқы бағалаудан бастап, қателерді түзету ретін шығарды. Ол әр түзетуді көпмүшені қалған қателік тұрғысынан қайта жазу үшін қолданды, содан кейін жоғары дәрежелі мүшелерді елемей, жаңа түзетуді шешті. Ол бұл әдісті туындылармен байланыстырмағаны және жалпы формуланы ұсынбағаны анық. Ньютон бұл әдісті сандық және алгебралық есептерге қолданды, соңғы жағдайда Тейлор қатарларын жасады.

Ньютон өз әдісін Виетаның ұқсас, бірақ дәл емес әдісінен алған болуы мүмкін. Виета әдісінің мәнін парсы математигі Шараф ад-Дин әл-Тусидің жұмысынан табуға болады, ал оның мұрагері Джамшид Әл-Каши N − ден тамырларды табу үшін x ^P -N = 0 шешу үшін Ньютон әдісінің формасын қолданды (Ypma 1995) . Квадрат түбірлерді есептеуге арналған Ньютон әдісінің ерекше жағдайы ежелгі заманнан бері белгілі және көбінесе вавилондық әдіс деп аталады.

Ньютон әдісін 17 ғасырдағы жапон математигі Секи Кова бір айнымалы теңдеулерді шешу үшін қолданды, дегенмен математикалық талдаумен байланыс болмады.

Ньютон әдісі алғаш рет 1685 жылы Джон Уоллистің тарихи және практикалық алгебра трактатында жарық көрді. [2] 1690 жылы Джозеф Рафсон analysis aequationum universalis кітабында жеңілдетілген сипаттаманы жариялады. [3] Рафсон бұл әдісті тек көпмүшелерге қолданды, бірақ ол бастапқы көпмүшеден әрбір келесі түзетуді алу арқылы Ньютонды қайта жазудың жалықтыратын процесінен аулақ болды. Бұл оған әр тапсырма үшін қайталанатын қайталанатын өрнекті шығаруға мүмкіндік берді. Ақырында, 1740 жылы Томас Симпсон Ньютон әдісін математикалық талдауды қолдана отырып, жалпы сызықтық емес теңдеулерді шешудің итеративті әдісі ретінде сипаттады, негізінен жоғарыда сипаттама берді. Сол басылымда Симпсон екі теңдеу жүйесіне жалпылау береді және Ньютон әдісін градиентті нөлге қою арқылы оңтайландыру есептерін шешу үшін қолдануға болатындығын атап өтеді.

Артур Кэйли 1879 жылы Ньютон-Фурьенің ойдан шығарылған тапсырмасында Ньютон әдісін 2-ден үлкен дәрежесі бар және күрделі бастапқы мәндері бар күрделі көпмүшелік тамырларға жалпылаудағы қиындықтарды бірінші болып байқады. Бұл рационалды функциялардың Итерация теориясын зерттеуге жол ашты. [2]

Ньютон (жанамалар) әдісінің негізі:

$\overline{x}$ -тің маңайындағы (1. 3) теңдеуінің түбірін іздеу үшін нүктені таңдап

аламыз және осы нүктенің маңайында Тейлор қатарына жіктейді:

$f\left( \overline{x} \right)$ = $f(x)$ + $f'\left( \overline{x} \right)$ ( $\overline{x} - x$ ) + …

Бұдан жуықтаудатылған теңдігі шығады

$f\left( \overline{x} \right) \approx f(x)$ + $f'\left( \overline{x} \right)$ ( $\overline{x} - x$ ) ,

$мұндағы\ f(x) = 0$ , мынаны шығаруға мүмкіндік береді

$\overline{x} \approx x - \frac{f(x) }{f'(x) }$ ,

келесі түрдегі итерациялық процесске әкеледі:

$x^{(n + 1) } = x^{(n) } - \frac{f\left( x^{(n) } \right) }{f'(x) }.$

[a; b] кесіндісінде $x_{0}$ туындылық нүктесін таңдаймыз- нөлдік жуықтау. Бұдан:

$x_{1} = x_{0} - \frac{f\left( x_{0} \right) }{f'\left( x_{1} \right) }$

табамыз, содан кейін

$x_{1} = x_{1} - \frac{f\left( x_{1} \right) }{f'\left( x_{1} \right) }$ .

Осылай теңдеудің түбірін табу процессі n х сандарын мына формуламен шығаруға келеді:

$x_{n} = x_{n - 1} - \frac{f\left( x_{n - 1} \right) }{f'\left( x_{n - 1} \right) }, \ n = 1, 2, 3\ldots$

Бұл процесс мына шарт орындалғанша: ${x}_{n} - x_{n - 1} < e$ .

жалғастырады. Мына шартта Ньютон әдісін жай итерациялар әдісінің нұсқасы ретінде қарастыруға болатыны анық:

$\varphi(x) = x - \frac{f(x) }{f'(x) }$ .

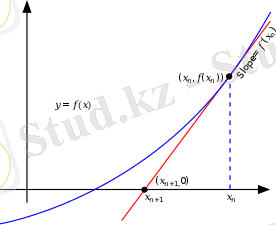
Illustration of Newton's method

1 - сурет.

1 сурет. $x_{n} + 1 - f$ функциясының $x$ түбірі үшін $x_{n}$ -ге қарағанда жақсы жуықтау (көк қисық) .

1. 3 Жартылай бөлу әдісі

Бұл әдіс үздіксіз функциялардың нөлдерін табуға бағытталған. Соңғы сұрыпталған массивті іздеу үшін екілік іздеу алгоритмі бөлімін қарау керек. Бастапқы диапазонда қолданылатын жартылай бөлу әдісінің бірнеше қадамдары [ $a_{1}, b_{1}$ ] . (Үлкен қызыл нүкте-бұл функцияның түбірі. )

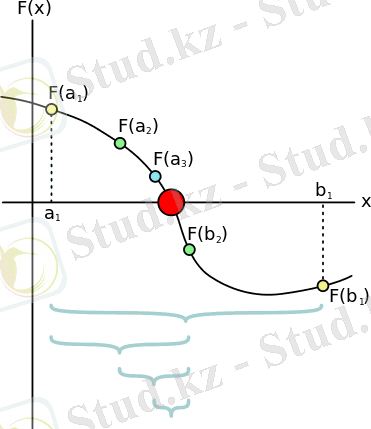
2 - сурет.

Математикада жартылай бөлу әдісі қарама-қарсы белгілері бар екі мән белгілі кез келген үздіксіз функцияға қолданылатын түбірді табу әдісі. Әдіс осы мәндермен анықталған интервалды бірнеше рет жартылай бөлуден, содан кейін функция белгіні өзгертетін ішкі интервалды таңдаудан тұрады, сондықтан түбір болуы керек. Бұл өте қарапайым және сенімді әдіс, бірақ ол салыстырмалы түрде баяу. Осыған байланысты, ол көбінесе шешімге дөрекі жақындау үшін қолданылады, содан кейін ол тезірек конвергентті әдістердің бастапқы нүктесі ретінде қолданылады. [8]

Көпмүшелер үшін түбірдің интервалда болуын тексерудің күрделі әдістері бар. Олар көпмүшенің барлық нақты тамырларын табудың тиімді алгоритмдеріне жартылай бөлу әдісін кеңейтуге мүмкіндік береді.

Әдіс нақты $x$ айнымалысы үшін $f(x) = 0$ теңдеуінің сандық шешімі үшін қолданылады, мұндағы $f$ - [ $a, b$ ] интервалында анықталған үздіксіз функция және $f(a)$ және $f(b)$ қарама-қарсы белгілері бар. Бұл жағдайда $a$ және $b$ түбірді жақшаға алады деп айтылады, өйткені аралық мәндер теоремасына сәйкес үздіксіз $F$ функциясы ( $a, b$ ) аралықта кем дегенде бір түбір болуы керек.

Әр қадамда әдіс интервалды осы нүктедегі $c = \frac{a + b}{2}$ интервалының ортаңғы нүктесін және $f(с) \$ функциясының мәнін есептеу арқылы екі бөлікке бөледі. Егер c түбір болса, онда процесс сәтті аяқталады және тоқтайды. Немесе және екі мүмкіндік бар: $f(a)$ және $f(с)$ қарама-қарсы белгілерге ие және түбірді жақшаға жабады немесе $f(с)$ және $f(b)$ қарама-қарсы белгілерге ие және түбірді жақшаға жабады. Осылайша, нөлдік $f$ бар интервалдың ені әр қадамда 50% - ға азаяды. Процесс интервал жеткілікті аз болғанша жалғасады.

Егер $f(с) =$ 0 болса, онда c-ның шешім ретінде қабылдануы мүмкін және процесс тоқтайды. Егер $f(a)$ және $f(с)$ қарама-қарсы белгілерге ие болса, онда әдіс с-ны $b$ үшін жаңа мән ретінде, ал егер $f(с)$ және $f(с)$ қарама-қарсы белгілерге ие болса, онда әдіс c-ны жаңа $a$ ретінде орнатады. екі жағдайда да жаңа $f(a)$ және $f(b)$ қарама-қарсы белгілерге ие, сондықтан әдіс осы кіші аралыққа қолданылады.

Егер $F(a, b)$ аралығындағы үздіксіз функция болса және $f(a)$ және $f(b)$ қарама-қарсы белгілерге ие болса, әдіс $f$ түбіріне жақындауға кепілдік беріледі. Абсолютті қателік әр қадамда екі есе азаяды, сондықтан әдіс сызықтық түрде жақындайды. Атап айтқанда, егер $c_{1} = \frac{a + b}{2}$ бастапқы интервалдың орташа нүктесі, ал $c_{n}\ \ n - нінші$ қадамдағы интервалдың орташа нүктесі, содан кейін $c_{n}\$ мен $с$ шешімі арасындағы айырмашылық шектеулі $\left c_{n} - c \right \leq \frac{b - a}{2^{n}}.$

Бұл әдісте түбірдің алғашқы жуықтауы ретінде $c_{0} = \frac{a + b}{2}$ нүктесі алынады. Пайда болған екі аралықтан [a, c ₀ ] және [b, c ₀ ], $F(a) \cdot F(b) < 0$ шарт бойынша тек түбір жатқан аралық алынады. Осы процедураны n рет қайталаймыз, яғни түбір жатқан аралықты 2 ⁿ рет кішірейтеміз. Интерацияны $\left F\left( c_{n} \right) \right < \varepsilon$ болғанша жүргіземіз, мұндағы ε -берілген өте аз шама болып табылады.

Жартылай бөлу әдісі үздіксіз функциялардың түбірлік теоремасына негізделген, ол кем дегенде бір түбірдің болуына кепілдік береді $\alpha$ функциялар $f$ аралықта $\ \lbrack a, b\rbrack$ егер $f(a)$ және $f(b)$ қарама-қарсы белгіге ие. Егер $\lbrack a, b\rbrack\ аралықта\ \ f$ функциясы да монотонды болса, яғни $f'(x) > 0$ барлық $x \in \lbrack a, b\rbrack$ үшін, содан кейін функцияның түбірі ерекше болады. Шешімнің бар екендігі анықталғаннан $a$ кейін алгоритм $x_{k}$ тізбегін түбір теоремасының гипотезасын қанағаттандыратын ені азаятын Интервалдардың орташа нүктелерінің тізбегі ретінде анықтайды. Аралығы белгілі түбірді нактылай табатын сандык әдістердің ең карапайым әдісі аралыкты жартылай бөлу әдісі. Әдістің мәні мынада: Бірінші кадам кезінде функция мәндері аралыктың басы мен соңында есептеледі. Содан кейін берілген аралыкты [a; b] екіге жартылай бөледі (х _і нүктесі) және осы нүктеде функция мәнін есептейді. Екіге бөлінген аралыктың кай жартысында функция мәні карама - карсы болса (таңбасы бойынша), осы аралыкты таңдаймыз (1 сурет) .

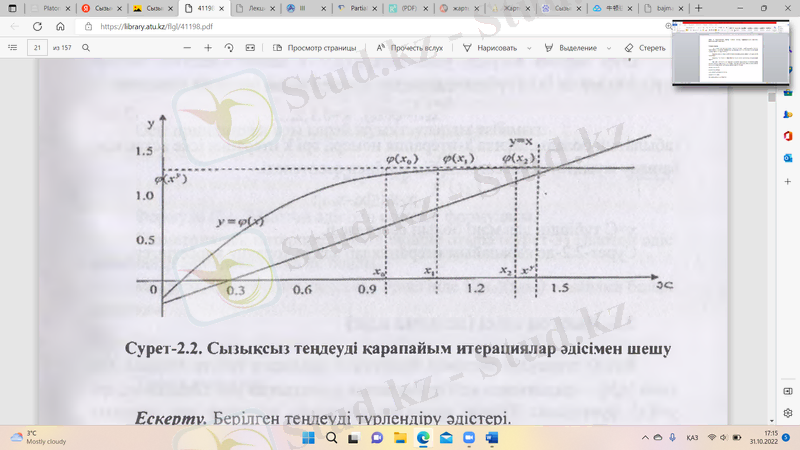
3 сурет. Сызықсыз теңдеуді қарапайым итерациялар әдісімен шешу

Алынған аралықты кайтадан екіге бөлген кезде, әрі осы нүктеде функция мәнін есептейді және аралық кайтадан таңдалады. Келесі аралықтың орта бір нүктесінде функция модулі кез-келген алдын ала берілген $\varepsilon$ санынан кіші болғанша, осы алгоритмді қайталап отырылады.

Жартылай белу тәсілінің алгоритмі келесі түрде кабылданады:

а _о =а, b _o =b, с _о =а _о =b _о

егер $F\left( a_{i} \right) \cdot F\left( b_{i} \right) f(x) = \left\{ \begin{array}{r} < 0, онда\ a_{i + 1} = a_{i} = b_{i + 1} = c_{i} = 0, \\ онда\ \ ac_{i + 1} = c_{i} > 0, \ \ \\ онда{\ \ a}_{i + 1} = c_{i}, b_{i} + 1 = b_{i} \end{array} \right. \$ (1. 4)

мұнда і=0, 1, 2, . . . , k.

Егер функция F(x) [a, b] аралығында үзіліссіз және аралық шектерінде әртүрлі таңбаларды кабылдайтын болған кезде, онда жартылай белу әдісі теңдеудің тура шешіміне х=С үйлеседі. [3]

Ньютон әдісі де, секант әдісі де қолданыстағы шешімнің табылуына кепілдік бере алмайды. Алайда, жартылай бөлу әдісі мұны жасай алады, егер бірнеше шешім болса, ол Ньютон әдісі мен секант әдісі сияқты олардың біреуін ғана табады. Жартылай бөлу әдісі басқа екі әдіске қарағанда баяу жұмыс істейді, сондықтан сенімділік жылдамдық шығындарымен бірге келеді.

Мысалы, $x^{2} - 9 = 0$ , $x \in \lbrack 0, 1000\rbrack$ жартылай бөлу әдісін қолдану арқылы шешу үшін келесідегідей пайымдайды. Бірінші негізгі идея: егер $f(x) = x^{2} - 9\$ интервалда үздіксіз болса және интервалдың соңғы нүктелері үшін функция мәндері ( $x_{L} = 0, x_{R} = 1000$ ) қарама-қарсы белгілерге ие болса, $f(x) \$ осін интервалда кем дегенде бір рет кесіп өтуі керек. Яғни, есеп шығарған кезде кем дегенде бір шешім бар екенін білуге болды.

Екінші негізгі идея интервалды екі тең бөлікке бөлуден туындайды, біреуі $x_{M} =$ 500 ортаңғы нүктесінің сол және оң жағында. $f\left( x_{M} \right)$ белгісін бағалау арқылы $x_{M}\$ -нің сол жағында немесе оң жағында шешім болуы керек екенін бірден білуге болады.

Егер $f\left( x_{M} \right)$ ≥0 болса, онда $f(x)$ функциясы $x_{L}$ мен $x_{M}$ арасындағы $x$ осін кем дегенде бір рет кесіп өтуі керек екені белгілі (бастапқы интервалмен бірдей аргументті қолдана отырып) . Сол сияқты, егер оның орнына $f\left( x_{M} \right)$ ≤0 болса, біз $f(x)$ функциясы $x_{M}$ мен $x_{R}$ арасындағы $x$ осін кем дегенде бір рет кесіп өтуі керек.

Қалай болғанда да, есеп шығарған кезде тек жарты аралықты жалғастыруға болады. Ерекшелігі, бұл $f\left( x_{M} \right)$ ≈0 болатын жағдай, бұл жағдайда шешім табылады. Бұл аралықты екі есе азайту шешім табылғанға дейін жалғасуы мүмкін. Бұл жағдайда" шешімі " $f\left( x_{M} \right)$ нөлге жақын болған кезде, дәлірек айтқанда: $f\left( x_{M} \right)$ < $\varepsilon$ , мұндағы $\varepsilon$ - пайдаланушы көрсеткен шағын сан. Сызылған стратегия ақылға қонымды болып көрінеді, сондықтан $F(x) = 0$ Жалпы алгебралық теңдеуін шеше алатын қайта қолданылатын функцияны жазу керек (bisection_method. py ) .

Жартылай бөлу әдісінде қажетті шарт: егер жартылай бөлу әдісінің бастапқы аралығы $a$ және $b$ -мен шектелсе және $n$ - қадамдағы шешім орташа мән ретінде қабылданса, онда есеп дұрыс болмайды.

2. Жобалау бөлімі

2. 1 Бағдарламаның сипаттамасы

Python бағдарламалау тілінде бағдарлама құрған кезде, әр процедураға мұқият болу керек, себебі егер есеп шығарған кезде әлде қандай қателік жіберіп дұрыс жазылмаса, онда есеп дұрыс шықпайда. Python-да әртүрлі математикалық операциялар бар. Математикалық операторлар көмегімен сызықтық емес теңдеулерді Ньютон әдісімен және жартылай бөлу әдісімен шығарады. Теңдеулерді шешудің сандық әдістері әлемінде жартылай бөлу әдісі өте сенімді, бірақ өте баяу.

Ньютон әдісін жартылай бөлу әдісімен сылыстырғанда Ньютон әдісі жылдам әрі жинақы жауап шығарып береді. Жартылай бөлу әдісінде конвергенция жылдамдығы сызықты, сондықтан ол баяу жұмыс жасайды. Ньютон әдісінде конвергенция жылдамдығы екінші ретті немесе квадраттық болып табылады, сол себепті де есеп шығарылған кезде жартылай бөлу әдісінен жылдам болады.

2. 2 Логикалық құрылымның сипаттамасы

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.