2-4 сынып оқушыларының бойы мен салмағы арасындағы корреляциялық байланыс


Абай облысы Жарма ауданы Жаңаөзен ауылы
«К. Шакенов атындағы орта мекатебі»
Зерттеу жұмысы
Тақырыбы:
Корреляция және корреляциялық байланыс
Орындаған: Байжуминоа Аружан
11-сынып оқушысы
Жетекшісі: Байгалиев Қайрат Сыдыкович
2022-2023 оқу жылы
«К. Шакенов атындағы орта мектебі»КММ 11-сынып оқушысы Байжуминова Аружанның «Корреляция және корреляциялық байланыс» атты зерттеу жұмысына
Пікір
Байжуминова Аружанның «Корреляция және корреляциялық байланыс» зерттеу жұмысы кіріспеден, үш тараудан, қорытындыдан және пайдаланылған әдебиеттерден тұрады. Оқушы ғылыми зерттеу жұмысының тақырыбын өз ынтасымен қалап, қызығушылықпен жасағаны байқалып тұр. Менің ойымша, оның бұл тақырыпты таңдап алуы қазіргі кезеңдегі осы тақырыптың маңыздылығы мен өзектілігі мен заманауилығына байланысты. Сондай-ақ ғылыми зерттеу жұмысы өз дәрежесінде жазылып, әрбір тарау мен бөлімдер мазмұны толығымен ашылған деп есептеймін. Оқушы іздене отырып, мектеп оқушыларының бойлары мен салмағын өлшеу, корреляциялық байланыс есептеу мәселесі бойынша өзіндік ой қорытқан.
Аружанның бұл зерттеу жұмысын жоғарыда көрсетілген негізге сүйене отырып, қорғауға жіберуді ұсынамын.
«К. Шакенов атындағы орта мектебі»КММ
математика пәні мұғалімі: Аманжолова Асия тиштыковна
Аңдатпа
Бұл жұмыста «корреляция» ұғымы, оны алғашқы ашқан ғалымдар туралы жазылған. Мектептің 2-ші және 4-ші сынып оқушыларының бойы мен салмағы туралы мәліметтер пайдаланып корреляциялық талдаулар жасалған.
Аннотация
В данной работе описывается понятие «корреляция» и учёные, впервые открывшие её. Корреляционный анализ проводился с использованием данных о росте и весе учащихся 2-х и 4-х классов школы.
Abstract
This work describes the concept of "correlation" and the scientists who first discovered it. Correlation analyzes were made using data on the height and weight of the 2nd and 4th grade students of the school.
Мазмұны
1. Кіріспе . . . 5-6
2. Негізгі бөлім . . . 7
2. 1. Корреляциялық байланыс түрлері . . . 7
2. 2. Ұлы математиктер . . . 8-9
2. 3. Корреляция коэффициентін есептеу . . . 9-14
3. Қорытынды. Корреляция жәнекорреляциялық байланыс . . . 15
4. Әдебиеттер тізімі, интернет ресурстары . . . 16
Кіріспе
Қазіргі кезде статистика ақпаратты алуға, өңдеуге және талдауға бағытталған білімнің ең маңызды саласы болып табылады. Жыл сайын енгізілетін ұғымдар осы ғылыммен байланысты адамдардың жұмысын айтарлықтай жеңілдетеді. Сіз оннан астам әртүрлі статистиканы атай аласыз: экономикалық, қаржылық, салықтық, демографиялық, медициналық, метеорологиялық және т. б.
Біз барлығымыз статистиканың қарапайым ұғымдарымен жақсы таныспыз: сандар қатарының режимі, орташа арифметикалық шама, таңдама және т. б. Жаңа ұғыммен танысайық.
Корреляция - зерттелетін құбылыстар арасында болатын статистикалық қатынасты көрсететін ұғым. Бұл жағдайда осы шамалардың біреуінің немесе бірнешеуінің өзгеруі басқа немесе басқа шамалардың жүйелі өзгеруіне әкеледі. Корреляция коэффициенті екі кездейсоқ шаманың корреляциясының математикалық өлшемі ретінде қызмет етеді.
Корреляция коэффициенті (r) - әр түрлі болуы мүмкін мән +1- ден -1- ге дейін. Толық оң корреляция кезінде бұл коэффициент + 1-ге тең, ал толық теріс корреляция кезінде - 1 болады. Корреляция коэффициентінің максималды мүмкін болатын абсолютті мәні r = 1, ал ең төменгісі r = 0.
Корреляция келесідей болуы мүмкін:
- r > 0, 7 кезінде күшті;
- 0, 5 < r < 0, 69 кезінде орташа;
- 0, 3 < r < 0, 49 кезінде орташа;
- 0, 2 < r < 0, 29 кезінде әлсіз;
- r< 0, 19 кезінде өте әлсіз.
- Жұмыс барысында мен тағы бір ұғымды қолданамын: корреляциялық талдау.
Корреляциялық талдау - екі немесе одан да көп айнымалылар арасындағы байланыстың күшін өлшейтін статистикалық деректерді өңдеу әдісі. Корреляциялық талдау регрессиялық талдаумен тығыз байланысты («корреляциялық-регрессиялық талдау» термині де жиі кездеседі, бұл жалпы статистикалық түсінік), оның көмегімен бірнеше регрессия теңдеуіне белгілі бір факторларды қосу қажеттілігін анықтайды, сонымен қатар бағалау сәйкестік байланыстары үшін алынған регрессия теңдеуі анықталған.
Регрессиялық талдау - X1, X2, …Xp бір немесе бірнеше тәуелсіз айнымалылардың Y тәуелді айнымалысына әсерін зерттеуге арналған статистикалық әдіс. Басқаша тәуелсіз айнымалылар регрессорлар немесе болжаушылар деп аталады, ал тәуелді айнымалылар критерийлер деп аталады.
Жұмыстың мақсаты: «корреляция» ұғымымен танысу. 2-ші және 4-ші сынып оқушыларының салмағы мен бойының корреляциясының мысалын көрсету.
Корреляция коэффициентін есептеу.
Тапсырмалар:
- Танымдық және ойын-сауық әдебиеттерін пайдалану;
- 2- және 4- сынып оқушыларының бойы мен салмағы туралы мәліметтер жинау;
- Корреляция коэффициентін есептеу үшін қажетті есептеулерді орындаңыз.
Гипотеза: 2-4-сынып оқушыларының бойы мен салмағының арасында корреляция бар деп есептеймін.
Зерттеу әдістері:
1. Оқу-сауықтыру әдебиеттерін талдау;
2. Корреляцияны есептеу үшін «корреляция» ұғымын қолдану;
3. 2 және 4 сынып оқушыларының бойы мен салмағы туралы мәліметтерді талдау.
2. 1. Корреляция байланыс түрлері.
Белгілі болғандай, бағыттары бойынша тура және кері корреляция бар.
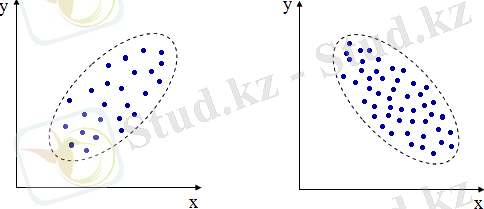
(тура «+») (кері «-»)
Тура, тәуелді айнымалы фактор атрибутының ұлғаюымен өскенде және кері, онда соңғысының өсуі функцияның төмендеуімен бірге жүреді. Мұндай қатынастарды сәйкесінше оң және теріс деп те атауға болады.
Күштілігі бойынша күшті және әлсіз байланыстар немесе олардың толық болмауы ерекшеленеді. Бұл формальды сипаттама нақты мәндермен көрсетіледі және нақты көрсеткіштер үшін қосылыс беріктігінің жалпы қабылданған критерийлеріне сәйкес түсіндіріледі.
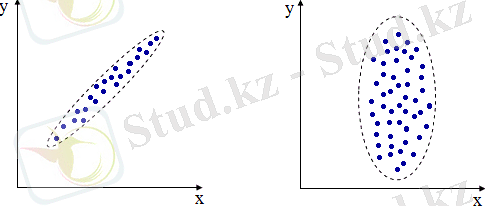
2. 2. Ұлы математиктер.
Қазіргі уақытта корреляция коэффициентін есептеудің әртүрлі әдістері бар. Ежелгі заманнан бері әртүрлі елдердің ғалымдары есептеудің ең оңай формуласын алуға тырысты. Мен формулаларын қолданатын математиктермен танысайық.
Карл Пирсон. (1857 ж. 27 наурыз - 1936 ж. 27 сәуір)
Карл Пирсон - ағылшын математигі, статистикі, биологы және философы; математикалық статистиканың негізін салушы, биометрияның негізін салушылардың бірі. 650-ден астам жарияланған ғылыми еңбектердің авторы. Орыс деректерінде оны кейде Чарльз Пирсон деп те атайды.
Математикалық статистика бойынша (400-ден астам еңбек) іргелі еңбектер жариялады. Корреляция теориясы, сәйкестік критерийлері, шешімдер қабылдау және параметрлерді бағалау алгоритмдері әзірленді. Мұндай кең таралған терминдер мен әдістер оның есімімен байланысты, мысалы:
Пирсон қисықтары
Пирсон үлестірімі
Пирсонның жарамдылық сынағы (хи-квадрат сынағы)
Пирсон корреляция коэффициенті және корреляциялық талдау
Дәрежелік корреляция
Көптік регрессия
Вариация коэффициенті
Қалыпты таралу және көптеген басқалар.
Пирсон өзінің жаңалықтарын қолданбалы салаларда, ең алдымен биология, медицинада қолдану үшін көп күш жұмсады. Бірқатар еңбектер философия мен ғылым тарихына қатысты. Қолданбалы математикалық статистика бойынша оның жұмысының көрнекті мұрагері Рональд Эйлмер Фишер болды.
Иоганн Бернулли-Пуассон.
(1667 ж. 27 шілде - 1748 ж. 01 қаңтар)
Иоганн 18 жасында (өнер) шебері болды, медицина оқуына ауысты, бірақ сонымен бірге математикаға қызығушылық танытты (медицинадан бас тартпаса да) . Ағасы Якобпен бірге ол Лейбництің дифференциалдық және интегралдық есептеу әдістері туралы алғашқы мақалаларын зерттеп, өзінің терең зерттеулерін бастады.
1691: Францияда болған кезде жаңа есептеулерді насихаттап, бірінші Париждік талдау мектебін құрады. Швейцарияға қайтып келгеннен кейін ол өзінің шәкірті Маркиз де Лопиталмен хат алысып, оған жаңа ілімнің екі бөлімнен тұратын мағыналы конспектісін қалдырды: шексіз аз есептеу және интегралдық есептеу.
Шексіз аз сандармен әрекеттердің тұжырымдамалық негізі ретінде Иоганн дәрістердің басында үш постулатты тұжырымдады (талдауды негіздеудің бірінші әрекеті) :
1) Шексіз аз мөлшерге азайтылған немесе ұлғайтылған мән азаймайды немесе өспейді.
2) Кез келген қисық сызық шексіз көп түзулерден тұрады, олардың өзі шексіз аз.
3) Екі ордината, абсциссалар айырымы және кез келген қисықтың шексіз аз бөлігінің арасына салынған фигура параллелограмм ретінде қарастырылады.
Кейінірек, өзінің оқулығын басып шығарған кезде, Лопитал біріншіден туындайтын 3-ші постулатты артық деп қабылдамады.
Сол 1691 жылы Acta Eruditorum-да Иоганнның алғашқы баспа жұмысы пайда болды: ол «тізбек сызығының» теңдеуін тапты (сол кезде көрсеткіштік функцияның болмауына байланысты құрылыс логарифмдік функция арқылы орындалды) . Сонымен қатар қисық сызықты егжей-тегжейлі зерттеуді Лейбниц пен Гюйгенс жүргізді.
2. 3. Корреляция коэффициентін есептеу.
Мен және 2 және 4 сынып оқушыларынан 15 баланың бойы мен салмағы туралы деректерді жинадым және алынған мәндерді 2 бағанға орналастырдым (x - 2 сынып оқушыларының бойы / салмағы, у - 4-сынып оқушыларының бойы / салмағы) және олардың квадраттары мен корреляция коэффициентін есептеуге қажетті көбейтінділерін таптым.


2-сынып оқушылары бойларының қосындысы 1911 см.
4-сынып оқушылары бойларының қосындысы 2206 см.
2-сынып оқушылары бойлары квадраттарының қосындысы 243689 см 2 .
4-сынып оқушылары бойлары квадраттарының қосындысы 324816 см 2 .
2-4-сынып оқушылары бойлары көбейтінділерінің қосындысы 281243 см 2 .
2-сынып оқушысының орташа бойы:
x = 1911 : 15 = 127, 5 см.
4-сынып оқушысының орташа бойы:
y = 2206 : 15 = 147, 1 см.
2 және 4 сынып оқушыларының бойлары көбейтіндісінің орташа мәні-
xy = 281243 : 15 = 18749, 5.
Сонымен қатар,
x*x = 243689 : 15 = 16246,
y*y = 324816 : 15 = 21654, 4.
Содан кейін стандартты ауытқуды есептедім:
Формула арқылы дисперсияны есептеу ыңғайлырақ:
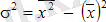
қарапайым түрлендірулер арқылы негізгіден алынады. Бұл жағдайда ауытқулардың орташа квадраты белгі мәндерінің квадраттарының орташа мәніне, орташа мәннің квадратын алып тастағанға тең болады.
Топталмаған деректер үшін:
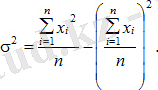
Топталған деректер үшін:
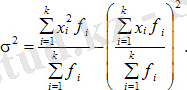
Дисперсия
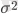 - ге тең.
- ге тең.
Функцияның дисперсиясы - опциялардың орташа мәнінен ауытқуының орташа квадраты, ол қарапайым және өлшенген дисперсиялар формулалары арқылы есептеледі.
Дисперсиялық қасиеттері:
атрибуттың барлық мәндері бірдей А тұрақты мәніне азайтылса немесе ұлғайтылса, дисперсия өзгермейді; егер мүмкіндіктің барлық мәндері бірдей есе азайса немесе көбейтілсе (k есе), онда дисперсия k2 есе азаяды немесе артады.
Есептеулер:
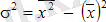
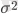 = 16256, 25 - 16246 = 10, 25
= 16256, 25 - 16246 = 10, 25
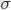 x = 3, 2
x = 3, 2
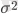 = 21654, 4 - 21638, 4 = 16/2=8
= 21654, 4 - 21638, 4 = 16/2=8
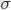 y = 2, 9
y = 2, 9
Содан кейін Бернулли-Пуассон формуласыr = (xy - x*y) /
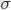 x
x
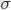 y арқылы корреляция коэффициентін есептедім.
y арқылы корреляция коэффициентін есептедім.
r = (18749, 5 - 127, 5*147, 1) /3, 2*2, 9 = -5, 75/9, 28 = -0, 6196
Осы жерден корреляция «кері» деген қорытынды жасауға болады, өйткені «-» белгісі бар және ол орташа.
Енді оқушылардың салмағын талдап көрейік.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz