Талдау мектеп оқулықтары және материалдар ҰБТ осы тақырып бойынша Арифметикалық және геометриялық прогрессиялар

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

КІРІСПЕ

«Сандар тізбегі» тақырыбы ежелгі дәуірде пайда болды және математика ғылымының дамуына үлес қосқан ғалымдардың есімдерімен байланысты әр түрлі тізбектерді зерттейді. Сандар тізбегіне байланысты көптеген мәселелер ежелгі уақытта пайда болған. «Сандар тізбегі» тақырыбы негізгі мектеп бағдарламасына енгізілген және базалық деңгейде, ең бастысы қарапайым сандық тізбектер - арифметикалық және геометриялық прогрессияны зерттеуге бағытталған. Алайда, нақты өмірде біз әртүрлі типтермен жиі кездесеміз тізбектер. Олардың көпшілігі әртүрлі ғылымдарда қолданылады. Мысалы, Фибоначчи сандары ежелгі тарихты хронологияда және кезеңдеуде, сәулет өнерінде, музыкада, биологияда, астрономияда, бағаны болжауда қолданылады, грек вазалары мен спираль тәрізді галактикалардың пішінін, күнбағыс пен ұлу үйінің құрылымын анықтайды. Н. Слоанның бүтін тізбектер туралы анықтамалық кітабында 2300 бүтін тізбектер жинақталған және тапсырыс берілген, бұл олардың қолдану аясы өте кең екендігін білдіреді.

Орта мектеп алгебра курсында «Арифметика және геометриялық прогрессиялар» тақырыбы бөлек оқылады, тек тоғызыншы сыныпта, мектеп бағдарламасының басқа бөлімдерімен аз ортақтықтары бар. Бірақ, бұған қарамастан, тек n-ші мүшенің формулаларын және бірінші n мүшесінің қосындыларын ғана емес, сонымен қатар арифметикалық және геометриялық прогрессиялардың қасиеттерін білу қажет есептер ҰБТ-да және жоғары оқу орнына түсу емтихандарында. Студенттің білімі жеткілікті жоғары деңгейде болуы үшін прогрессияны зерттеу кезінде оның танымдық белсенділігін белсендіру қажет. Геометриялық және арифметикалық прогрессиялар мектептің алгебра курсында ғана емес өмірде қолданыста маңызды рөл атқарады.

Өмірде қолдану аясы өте кең. Мысалы, химияда арифметикалық прогрессияда температура көтерілген сайын, химиялық реакциялардың жылдамдығы геометриялық прогрессияда өседі. Әдебиетте: « . . . Ол хореядан иамба бола алмады, өйткені біз ажырату үшін күрескен жоқпыз . . . ». Ямбия мен хореяның айырмашылығы өлеңнің екпінді буындарының әр түрлі орналасуында. Iambic - бұл 2, 4, 6, 8, жұп буындарына баса назар аударатын поэтикалық метр . . . Стресті буындардың сандары арифметикалық прогрессияны 2-ші мүшемен және 2-ші прогрессиямен айырмашылықты құрайды. Хорея - бұл поэтикалық метр өлеңнің тақ буындарына екпін беру. Стресті буындардың сандары арифметикалық прогрессияны құрайды 1, 3, 5, 7, . . . және т. б. ҰБТ тапсырмаларында математикадан сонымен қатар арифметикалық және геометриялық прогрессияларды қолдануға арналған, бірақ практикалық мазмұны бар тапсырмалар бар. Сондықтан, студент мектеп курсынан өзіне белгілі материалды қайталап, тіпті көптеген жаңа және қызықты нәрселерді білуі үшін бұл курстың толық сипаттамасын беру өте маңызды. Бұл қорытынды біліктілік жұмысы тақырыбының өзектілігі.

Зерттеу нысаны - тақырыпты ұсыну процесі.

Ақпараттық-коммуникациялық технологияларды қолдана отырып, мектептегі математика курс да «дәйектілік».

Нәрсе зерттеу: Мүмкіндіктер зерттеу арифметикалық ақпараттық-коммуникациялық технологиялар арқылы геометриялық прогрессия.

Қашан орындау жұмыс болды қолданылған келесісі зерттеу әдістері:

1. Таңдалған тақырыптың теориялық негіздерін зерттеу;

2. Талдау мектеп оқулықтары және материалдар ҰБТ осы тақырып бойынша «Арифметикалық және геометриялық прогрессиялар»;

3. Зерттеу тақырыбы бойынша тест тапсырмаларын өздігінен таңдау;

4. Дамуы әдістемелік ұсыныстар арқылы ақпараттық-коммуникациялық технологияларды қолданатын тақырып «Арифметикалық және геометриялық прогрессиялар».

Қорытынды біліктілік жұмысын аяқтау барысында оның құрылымы анықталды: мазмұны, теориялық және практикалық бөлігі, қорытынды, пайдаланылған әдебиеттер тізімі.

Кіріспеде өзектілік негізделеді, қорытынды жұмыстың мақсаты мен міндеттері қойылады, оларды шешу әдістері келтірілген.

Бірінші тарауда тақырып бойынша барлық теориялық материалдар бар

«Арифметикалық және геометриялық прогрессиялар». Негізгі ұғымдардың анықтамалары берілген, прогрессия мүшелерінің қасиеттері, арифметикалық және геометриялық прогрессияның алғашқы n-мүшелерінің қосындысы қарастырылған. Зерттеу тақырыбын ұсыну бойынша мектеп оқулықтарына талдау жасалды.

Екінші тарауда тақырып бойынша зерттеудің практикалық бағыты келтірілген.

Қорытындысында атқарылған жұмыстардың нәтижелері келтірілді.

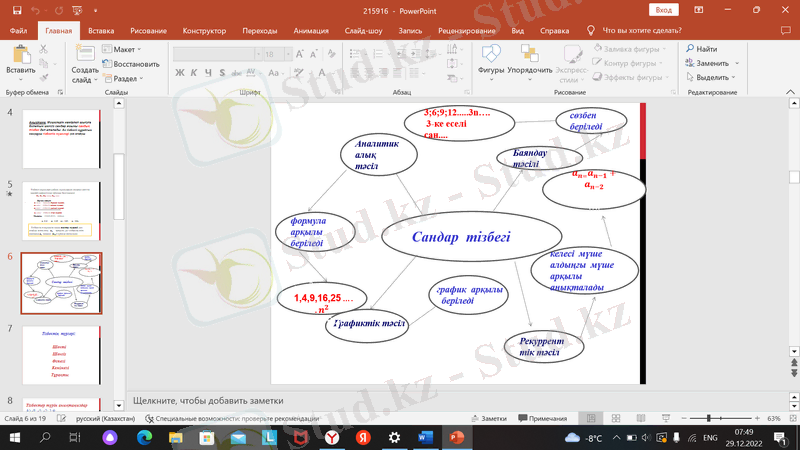
САНДЫҚ ТІЗБЕКТЕР ТУРАЛЫ АНЫҚТАМА

Анықтама . Мүшелерін нөмірлеп шығуға болатын шексіз сандар жиыны сандық тізбек деп аталады. Ал тізбекті құрайтын сандарды тізбектің мүшелері деп атайды.

Тізбекті мүшелері сәйкес мүшелердің индексі (реттік нөмірі) көрсетілген әріппен белгіленеді:

a ₁ , a ₂ , a ₃ , . . . , a _n , . . .

Берілген жазуда:

а ₁ саны - тізбектің бірінші мүшесі;

a ₂ саны - тізбектің екінші мүшесі;

a ₃ саны - тізбектің үшінші мүшесі;

a _n саны - тізбектің n-ші мүшесі;

Мысалы, 2; 4; 6; 8; 10; 12; . . . тізбекте

а ₁ =2; а ₅ =10; а ₁₂ =24; а _n =2n;

1. 2 МАТЕМАТИКА МЕКТЕБІНІҢ КУРСЫНДА ІЛІКТІЛІКТІ ЗЕРТТЕУДІҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

Тізбектегі шектеулі мүшелер болуы мүмкін екенін ескеріңіз. Бұл жағдайда оны ақырғы деп атайды. Шекті тізбектің мысалы ретінде екі таңбалы сандар тізбегін келтіруге болады: 10; он бір; 12;

13; . . . , 98; 99.

Кезектілікті көрсету үшін кез-келген санмен қатардың мүшесін табуға мүмкіндік беретін әдісті көрсету керек.

Жиі рет n санының функциясы ретінде оның n-ші мүшесін білдіретін формуланы қолдану арқылы берілген. Бұл формула тізбектің n-ші мүшесінің формуласы деп аталады. Мысалы, оң жұп сандар тізбегін аn = 2 n формуласы, ал тізбегі арқылы анықтауға болады

Нөмірі 1-ге тең тұрақты бөлшектер, формула бойынша . . .

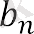1-мысал . . . Уn = формуласы бойынша реттілік берілсін n ^{2018-04-21 121 2} - 3 n.

Оның мүшелерінің алғашқы бесін есептейік.

1, 2, 3, 4, 5 натурал сандарын n орнына қойып, аламыз: y 1 = - 2,

y 2 = - 2, yz = 0, y 4 = 4, y 5 = 10.

2-мысал . . . Тізбектің бірінші мүшесі (аn) 3-ке тең болсын, ал әрбір келесі мүше алдыңғы квадратқа тең, яғни. a 1 = 3, және n + 1 =

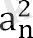
Аn + 1 = аn + 1 = формуласын қолдану 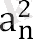тізбектің белгілі бірінші мүшесінен екіншісін есептеуге болады, содан кейін белгілі секундтан үшіншісін табуға болады және т. б. 3, 9, 81, 6561, . . . ретін аламыз . . .

4-ке бөлгенде 1: 1, 5, 9, 13, 17, 21, . . . Оның әрбір мүшесі, екіншісінен бастап, алдыңғы мүшеге 4 санын қосу арқылы алынады. Бұл реттілік арифметикалық прогрессияның мысалы болып табылады.

Арифметикалық прогрессия

Анықтама. Арифметика прогрессия деп аталады әр мүше, екіншісінен бастап, сол санға қосылған алдыңғы мүшеге тең болатын реттілік.

Егер кез-келген натурал n үшін келесі шарт орындалса, (an) тізбегі арифметикалық прогрессия болатындығын ескеру маңызды:

a т + 1 = аn + d, (1)

мұндағы d - бірнеше сан.

Арифметикалық прогрессияның анықтамасынан оның кез-келген мүшесінің екіншісінен бастап алдыңғы мүшесінің айырмашылығы d-ге тең болатындығы шығады, яғни. кез-келген натурал сан үшін келесі теңдік орын алады: аn + 1 - аn = d.

D саны арифметикалық прогрессияның айырымы деп аталады.

Арифметикалық прогрессияны орнату үшін оның бірінші мүшесі мен айырмашылығын көрсету жеткілікті.

Міне бірнеше мысал:

1-мысал . . . Егер a 1 = 1 және d = 1 болса, онда арифметикалық прогрессия аламыз: 1, 2, 3, 4, 5, . . . , олардың мүшелері қатарынан натурал сандар болады.

2-мысал . . . Егер a 1 = 1 және d = 2 болса, онда біз арифметикалық прогрессия аламыз: 1, 3, 5, 7, 9, . . . , бұл оң тақ сандар тізбегі.

3-мысал . . . Егер a 1 = - 2 және d = - 2 болса, онда берілген арифметикалық прогрессия:

- 2, - 4, 0, 8, 10, . . . - теріс жұп сандар тізбегі. Мысал 4. Егер a 1 = 7 және d = 0 болса, онда бізде арифметикалық прогрессия болады: 7,

7, 7, . , барлық мүшелері тең.

Бірінші мүшені және арифметикалық прогрессияның айырмашылығын біле отырып, оның кез-келген мүшесін екінші, үшінші, төртінші және тағы басқа мүшелерді бірінен соң бірін есептеу арқылы табуға болады. Бірақ прогрессияның үлкен санымен мүшесін табу үшін бұл әдіс қолданылады ыңғайсыз. Аз есептеу жұмысын қажет ететін әдісті табуға тырысамыз.

Арифметикалық прогрессияның анықтамасы бойынша a2 = a1 + d,

a3 = a2 + d = (a 1 + d) + d = a 1 + 2d, a4 = a3 + d = (a 1 + 2d) + d = a 1 + 3d, a5 = a4 + d = (a 1 +) 3d) + d = a 1 + 4d.

Дәл осылай a 6 = a 1 + 5 d, a 7 = a 1 + 6 d болатындығын анықтаймыз, ал жалпы ан табу үшін 1-ге (n - 1) d қосу керек, яғни.

ан= a 1 + d * (n- 1) (2)

Арифметикалық прогрессияның n-ші мүшесінің формуласын алдық. Мұны математикалық индукция әдісімен дәлелдейік.

N = 1 үшін бұл формула дұрыс: a 1 = a.
(2) формуласы n = k, k> 1 үшін ақиқат делік, яғни. ak = a 1

+ d (k - 1) .

Ak + 1 арифметикалық прогрессиясының анықтамасы бойынша Мұндағы k мүшесін өрнектің орнына ak + 1 = a 1 + d (k - 1) аламыз

+ d = a + dk, және бұл n = k + 1 үшін формула (2) .

Математикалық индукция принципінен (2) формуланың кез-келген натурал сан үшін ақиқат екендігі шығады.

Q. E. D.

Осы формуланы пайдаланып есептер шығаруға мысалдар келтірейік.

1-мысал . . . Рет (cn) - с 1 = 2, 3 және d = 0, 45 болатын арифметикалық прогрессия. Осы прогрессияның оныншы және жүзінші мүшелерін табайық.

Бізде: c 10 = 2, 3 + 0, 45 - 9 = 2, 3 + 4, 05 = 6, 35

100 = 2. 3 + 0. 45 - 99 = 2. 3 + 44. 55 = 46. 85 болғанда.

2-мысал . . . 71 саны арифметикалық прогрессияның мүшесі екенін анықтайық (xn) : - 10, - 5, 5, - 1, 3, 5, . . .

IN берілген арифметикалық прогрессия xn = - 10 және г. =

x 2 - x 1, d = -5, 5 - (- 10) = 4, 5. Прогрессияның n-ші мүшесінің формуласын жазайық

xn = - 10+ 4, 5 (n - 1), яғни. xn = 4, 5 n- 14, 5.

Нөмір 71 болып табылады мүшесі арифметикалық прогрессия (xn), егер а бар өрнектің мәні болатындай n nатурал саны (4, 5 n

он төрт, 5) 71-ге тең. 4, 5 n-14, 5 = 71 теңдеуін шешейік.

Аламыз: 4, 5 n = 85, 5, n = 19.

Бұл 71 саны осы арифметикалық прогрессияның мүшесі екенін білдіреді. Арифметикалық прогрессияның n-ші мүшесінің формуласы n + d (n- 1 ) =бірақ

басқаша жазуға болады: а _n = d _n + (а ₁ - d) .

Демек, кез-келген арифметикалық прогрессияны а _n = к _n + b формуласы арқылы беруге болатыны анық, мұндағы k және b бірнеше сандар.

Керісінше де дұрыс: форманың формуласымен берілген реттілік (аn)

Ан= kn + b, мұндағы k және b - кейбір сандар, арифметикалық прогрессия.

Шынында да, (аn) реттіліктің (n + 1) th және n-ші мүшелері арасындағы айырмашылықты табамыз:

ан ₊ _бір - аn = k (n + 1) + b- (kn + b) = kn + k + b- kn- b = k

Демек, кез-келген n үшін аn +1 = аn + k теңдігі ақиқат, ал анықтамасы бойынша (аn) тізбегі арифметикалық прогрессия болады. Бұл прогрессияның айырымы k-ге тең екенін ескеріңіз.

Арифметикалық прогрессияның қасиеттері.

Арифметикалық прогрессияның әрбір мүшесі, екіншісінен бастап, көршілес мүшелерінің арифметикалық ортасына тең, яғни. k> 2 үшін формула дұрыс болады

а _қ = . . . (3)

Шынында да, k ≥ 2 үшін бізде ak = ak - 1 + d және ak = ak +1 - d болады. Осы теңдіктердің мүшесін шарт бойынша қосқанда, 2аk = аk - 1 + аk +1 аламыз, қайдан (3) шығады.

Шекті арифметикалық прогрессияның 1, a 2, . . . , және n оның ұштарынан бірдей қашықтықта орналасқан мүшелердің қосындысы экстремалды мүшелердің қосындысына тең, яғни. k = 1, 2 үшін,

. . . , n дұрыс формула ақ+ аn - k +1 = а 1 + аn. (4)

Шынында да, ақырлы арифметикалық прогрессияда a 1, a 2, . . . , және ak және an - k +1 мүшелері ұштардан бірдей қашықтықта орналасқан. (2) формула бойынша аk = а 1 + d (k - 1) және аn - k +1 = а 1 + d (n - k) . Осы мүшелердің қосындысы ak + an - k +1 = 2 a 1 + d (n) -ке тең

1) және экстремалды мүшелердің қосындысына тең a 1 + an = 2 a + d (n - 1) .

Алғашқы жүз натурал санның қосындысын тапқыңыз келеді делік. Бұл мәселені сандарды тікелей қоспай-ақ қалай шешуге болатындығын көрсетейік.

Қажетті қосынды S-мен белгілеп, оны екі жағдайда жазайық, бірінші жағдайда терминдерді өсу ретімен, екіншісінде кему ретімен орналастырайық: S = 1 + 2 + 3 + . . . + 98 + 99 + 100,

S = 100 + 99 + 98 + . . . + 3 + 2 + 1.

Бірінен соң бірі орналасқан сандардың әр жұбы 101-ге дейін қосады.

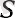Мұндай жұптардың саны 100.

Ұқсас пайымдаудың көмегімен кез-келген арифметикалық прогрессияның алғашқы мүшелерінің қосындысын табуға болады.

Сома мүшелері түпкілікті арифметикалық прогрессия теңэкстремалды мүшелердің жарты қосындысының терминдер санына көбейтіндісі, т. а. егер а

Sn= a1 + a2 + - + an-1 + an,

содан кейін Sn = . . .

Шынында да, егер Sn = a1 болса

+ a2 +… + an-1 + an, содан Sn = an + an-1 +… + a2 + a1.

Осы теңдіктердің мерзімін терминге қосып, 2 қасиетін пайдаланып, біз 2Sn аламыз

= (а1 + аn) + (а2 + аn-1) + . . . + (а1 + аn) = n (а1 + аn), қайдан (5) формула шығады.

Міне бірнеше мысал:

1-мысал . . . 1, 3, 5 арифметикалық прогрессияның алғашқы жиырма мүшесінің қосындысын табыңыз . . .

Бұл арифметикада а 1 = 1, d = 3, 5 - 1 = 2, 5 прогрессиялары. N-ші мүшесінің формуласы бойынша біз прогрессияның жиырмасыншы мүшесін табамыз:

a ₂₀ = 1 + 2, 5 • 19 = 48, 5

Енді алғашқы жиырма мүшенің қосындысын есептейік:

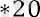
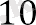S ₂₀ =

Егер арифметикалық прогрессияның бірінші мүшесі мен айырмасы берілген болса, онда басқа формада ұсынылған қосынды формуласын қолдану ыңғайлы екеніне назар аударыңыз. A1 + d (n - 1) өрнегінің орнына (5) формуласына (an) ауыстырыңыз аламыз:

Sn =, яғни Sn = (6)

Егер қарастырылып отырған мәселені шешу үшін (6) формуланы қолдансақ, онда есептеулер келесідей болады:

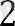
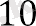S20 =

2-мысал . . . Аn = 5 n - 4 формуласымен берілген (аn) реттіліктің алғашқы отыз мүшесінің қосындысын табайық.

(Аn) реттілігі арифметикалық прогрессия болып табылады, өйткені ол аn = kn + b формуласымен берілген, мұндағы k = 5 және k = - 4.

Осы арифметикалық прогрессияның бірінші және отызыншы мүшелерін табайық: a1 = 5 * l - 4 = 1, a 2 = 5 * 30 - 4 = 146.

Енді (5) формуланы пайдаланып, S 30 есептейміз:

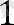
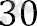
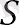
3-мысал . . . 1 + 2 + 3 +… + n қосындысын табыңыз, шарттар онда барлығы 1-ден n-ге дейінгі натурал сандар орналасқан.

Арифметикалық прогрессияға (5) формуланы қолдану; 2; 3; . . . , біз 1 + 2 + . . . + n = аламыз . . .

4 мысал . . . Барлық натурал сандардың алтыға бөлінетінін емес, қосындысын табайық 250-ден асады.

Табиғи сандар, еселіктер алты, форма арифметикалық прогрессия, оны формула бойынша беруге болады = 6 n. Табу,

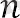
бұл прогрессияның қанша мүшесі 250-ден аспайды, біз 6n <250 теңсіздігін шешеміз. Аламыз . . .

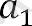
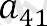
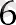
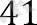
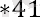Бұл дегеніміз, прогрессияның мүшелерінің саны, олардың қосындысын табу керек - 41. Бізде:

1. 5. Геометриялық прогрессия

Табиғи көрсеткіштері бар мүшелер дәрежесі 2 болатын тізбекті қарастырайық: 2; 22; 23; 24; . . . ;

Осы тізбектің әрбір мүшесі, екіншіден бастап, алдыңғы мүшені 2-ге көбейту арқылы алынады, бұл тізбек геометриялық прогрессияның мысалы болып табылады .

Анықтама. Геометриялық прогрессия деп аталадынөлдік емес сандар тізбегі, онда әр мүше, екіншісінен басталып, алдыңғы мүшеге бірдей санға көбейтіледі.

Басқаша айтқанда (bп) реттілігі геометриялық прогрессия болып табылады, егер кез келген табиғи n үшін келесі шарттар орындалса:

бн≠ 0 және bп + 1 = bn * q (1)

мұндағы q - бірнеше сан. Мысалы, (bn) 2 санының натурал қуатының кезектілігімен белгілейік, бұл жағдайда кез-келген натурал n үшін bп + 1 = bn * 2 теңдігі шын болады; мұнда q = 2.

Геометриялық прогрессияның анықтамасынан оның кез-келген мүшесінің, екіншісінен бастап, алдыңғы мүшесіне қатынасы q, яғни шығады. кезінде

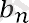кез келген табиғи n келесі теңдік шындыққа сәйкес келеді: q.

Q q бөлгіш деп аталады геометриялық прогрессия. Геометриялық прогрессияның бөлгіші нөлге тең емес екені анық.

Геометриялық прогрессияны орнату үшін оның бірінші мүшесін және бөлгішін көрсету жеткілікті.

Міне бірнеше мысал:

Мысал бір . . . Егер b 1 = бір және q = 0, 1, онда біз геометриялық прогрессия аламыз: 1, 0, 1, 0, 01, 0, 001, 0, 0001, . . .

2-мысал . . . B1 = шарттары -2 және q = 3 геометриялық прогрессия -2, -6, -13, -54, -162, . . . берілген.

Мысал 3 . . . Егер а б _бір = 4 және q = -3, содан кейін Бізде бар прогрессия: 4, -12. 36, -

103, 324, . . .

Мысал төрт . . . Егер а б _бір = 8 және q = бір, содан кейін алу геометриялық прогрессия 8, 8, 8, . . .

Геометриялық прогрессияның бірінші мүшесі мен бөлгішін біле отырып, сіз екінші, үшінші, сондай-ақ оның кез-келген мүшесін кезекпен таба аласыз:

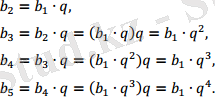
Дәл сол сияқты біз b6 = b1 * q5 болатынын анықтаймыз және Жалпы, (bn) табу үшін b1-ді qn-1-ге көбейту керек, яғни bn = b1 * qn-1. (2)

біз алды формула nth мүше геометриялық прогрессия.

Мұны математикалық индукция әдісімен дәлелдейік.

Формула (2) n = 1 үшін анық.
Ол $ n = k, k-1 $ үшін де дұрыс болсын, яғни. bk = bn • qk-1.
(1) -ден bk + 1 = b1qk, яғни (2) формула n = k үшін де дұрыс болатындығы шығады

+ 1.

Of принцип математикалық индукция келесі, не формула (2)

n [7] кез-келген натурал санына жарамды.

Q. E. D.

Осы формуланы пайдаланып есептер шығаруға мысалдар келтірейік. Мысал 1. Геометриялық прогрессияда b 1 = 0, 8 және q =. B10 табайық. Геометриялық прогрессияның n-ші мүшесінің формуласы бойынша

. . .

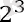
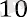
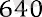
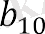2-мысал . . . B1 болса, геометриялық прогрессияның сегізінші мүшесін табыңыз (bn)

= 162 және b3 = 18.

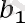
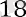
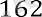Геометриялық прогрессияның бірінші және үшінші мүшелерін біле отырып, оның бөлгішін табуға болады. B3 = b1 * q2 болғандықтан q2 = болады . . .

Q2 = теңдеуін шешіп, q = болатынын анықтаймыз немесе q = . . .

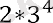Сонымен, есептің шартын қанағаттандыратын екі прогрессия бар.

3-мысал . . . Сұйылтылатын сорғының поршенінің әр қозғалысынан кейін

ыдыс ондағы ауаның 20% жойылады. Алғашқы қысым 750 мм сынап бағанасын құраса, алты поршендік қозғалыстан кейін ыдыстың ішіндегі ауа қысымын анықтайық. Өнер.

Поршеньнің әр қозғалысынан кейін ыдыстан 20% қол жетімді ауа шығарылатындықтан, 80% ауа қалады. Поршеньдің келесі қозғалысынан кейінгі ыдыстағы ауа қысымын білу үшін алдыңғы поршеньдік қозғалыстан кейінгі қысымды 0, 8-ге көбейту керек.

Бізде геометриялық прогрессия бар, оның бірінші мүшесі 760, ал азайтқышы 0, 8. Поршеньдік алты қозғалыстан кейін ыдыстағы ауа қысымын білдіретін (мм рт. ) Сан осы прогрессияның жетінші мүшесі болып табылады. Ол 750 * (0, 8) 6-ға тең.

Есептеулер жасағаннан кейін біз мынаны аламыз:

750 * (0, 8) 6 750 * 0, 26 200 (мм сынап бағанасы)

Геометриялық прогрессияның қасиеттері.

Геометриялық прогрессияның әрбір мүшесінің квадраты, екіншісінен бастап, көршілес мүшелердің көбейтіндісіне тең, яғни k ≥ 2 үшін дұрыс формула

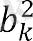(3)

Егер геометриялық прогрессияның барлық мүшелері оң болса, онда бұл қасиет келесідей тұжырымдалады: геометриялық прогрессияның әрбір мүшесі, екіншісінен бастап, көршілес мүшелерінің геометриялық ортасына тең, яғни.

. . .

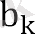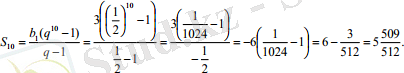Прогрессияның бірінші мүшесі мен бөлгіші белгілі болғандықтан, есепті шығару үшін (8) формуланы қолдану ыңғайлы. Біз алып жатырмыз:

2-мысал . . . 1 + x + . . . + xn - 1 (x ≠ 1) қосындысын табыңыз, оның мүшелері 1 геометриялық прогрессияның кезектес мүшелері; х; x 2, . . .

Прогрессияның бірінші мүшесі 1-ге тең, ал бөлгіш x-ге тең. Xn-1 n саны бар осы прогрессияның мүшесі болғандықтан, оның бірінші n мүшесінің қосындысын табу міндеті қойылды. (7) формуласын қолданайық:

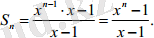
Сонымен, 1 + x +… + xn-1 =.

Соңғы теңдіктің сол және оң жақтарын х-1-ге көбейтіңіз. Xn-1 = (x-1) (1 + x +… + xn-1) сәйкестілігін аламыз.

Егер соңғы ондық бөлшекпен ұқсастығы бойынша 0. . . . шексіз ондық бөлшегін цифрларға кеңейтсек, онда біз шексіз мүшелер санымен қосынды аламыз: 0. 03 + 0. 003 + 0. 0003 + . . .

Осы қосындыдағы терминдер 0, 3 геометриялық прогрессияның мүшелері; 0, 03; 0, 003; 0. 0003; … Q = 0, 1-мен.

Геометриялық прогрессияның алғашқы n мүшесінің қосындысының

формуласы бойынша бізде:

Sn = . . .

Қашан n терминдер санының, (0, 1) n өрнектің шексіз өсуі

нөлге ерікті түрде жақын болады, демек, бүтін бөлшек нөлге шексіз жақындайды, демек, бүтін бөлшек шектеусіз нөлге ұмтылады.

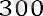Шынында да, егер n = 2 болса, онда ; егер n = 3, содан кейін

;

егер а n = 4, содан кейін, егер а n = 5, содан кейін

;

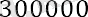сондықтан кезінде шектеусіз ұлғаюда n айырмашылық 3 санына ерікті түрде жақындайды немесе олар айтқандай,

санға ұмтылады.

Сонымен, геометриялық прогрессияның алғашқы n мүшесінің қосындысы 0, 3; 0, 03; 0, 003; 0. 0003; . . . n-нің шексіз ұлғаюына ұмтылады

сан . . . Бұл мәлімдеме 0, 3 + 0, 03 + 0, 003 + 0, 0003 + . . . = теңдік түрінде жазылған _{. . .}

Нөмір деп аталады шексіз геометриялық прогрессияның қосындысы 0, 3; 0, 03; 0, 003; 0. 0003; . . .

Қарастырайық Қазір ерікті геометриялық прогрессия b1;

b1q; b1q2; . . . , кезінде қандай q <1.

Прогрессияның алғашқы n мүшесінің қосындысының формуласын жазайық: 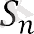Біз теңдіктің оң жағындағы өрнекті түрлендіреміз:

. . .

Ескертіп қой

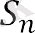
Егер q болатындығын дәлелдеуге болады <1, содан кейін n-нің шексіз өсуімен qn коэффициенті нөлге ұмтылады, сондықтан нөлге ұмтылады және көбейтінді

. . . Сондықтан n шексіз өсуімен S қосындысы санға ұмтылады . . .

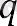Нөмір деп аталады сома шексіз геометриялық прогрессия (bn) бірге <1.

онда олар оны былай жазады: b1 + b1q + b1q2 + . . . =

Прогрессияның қосындысын (bn) S әрпімен белгілеп, формуласын аламыз

S = (9)

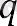Егер q > 1, онда Sn геометриялық прогрессиясының алғашқы n мүшесінің қосындысы n-нің шексіз өсуімен ешқандай санға бейім емес. Шексіз геометриялық прогрессияның қосындысы <1 ғана болады.

1-мысал . . . 12 шексіз геометриялық прогрессияның қосындысын табыңыз; -

төрт; ; . . .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.