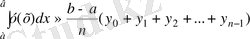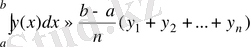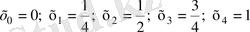Анықталған интегралда айнымалыны ауыстыру

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 34 бет
Таңдаулыға:

1 Интегралды есептеу әдістерінің теориялық негіздері

0.1 Интеграл ұғымы, анықтамасы және қасиеттері

Интеграл (латынша integer - бүтін) - математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан туындысы бойынша функцияны іздеуден, екінші жағынан - ауданды, көлемді және доға ұзындығын өлшеуден, күштің белгілі бір уақыт ішінде атқарған жұмысын табудан шықты. Осыған сәйкесті интеграл анықталмаған және анықталған интерал болып бөлінеді. Міне, осыларды есептеу интегралдық есептеудің міндеті болып табылады. Анықталған интегралды әр түрлі әдістермен шешуге болады.
Анықталмаған интеграл
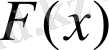және функциялары 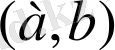сан аралығында анықталған және үзіліссіз функция болсын.
Анықтама. Егер 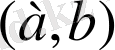аралығында дифференциалданатын 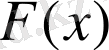функциясы
немесе (1)
(1) теңдіктерін барлық 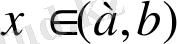үшін қанағаттандырса, онда осы аралықта үзіліссіз 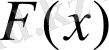функцияс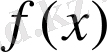ы функциясының алғашқы функциясы деп аталады.
Егер берілген f(x) функциясының алғашқы функциясы F(x) болса, онда бұдан басқа алғашқы функциялардың түрі 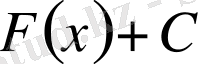болады.
Анықтама. 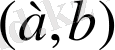аралығындағы 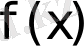функциясының барлық алғашқы функцияларының жиыны осы функцияның анықталмаған интегралы деп аталады.
Оны 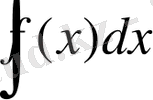таңбасымен белгілейді.
Алғашқы функциялардың бар болуы туралы негізгі теорема.
Теорема. Кез келген үзіліссіз функцияның шексіз көп алғашқы функциялары болады.
Егер 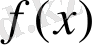функциясының алғашқы функцияларының бірі 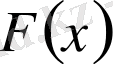болса, кез келген басқасын 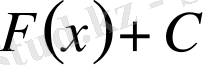(2) түрінде өрнектеуге болады:
, (2)
мұндағы анықталмаған интеграл таңбасы, 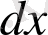- 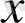айнымалысының дифференциалы, 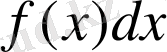- интеграл астындағы өрнек, ал 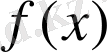- интеграл астындығы функция, 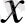- интегралдау айнымалы; С - тұрақты.
Берілген функцияның алғашқы функциясын табу интегралдау амалы деп аталады.
Теорема(анықталмаған интегралдың бар болу шарты). Егер 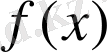функциясы үзіліссіз болса, онда оның анықталмаған интегралы бар болады.
Анықталмаған интегралдың қасиеттері. Анықталмаған интегралдың анықтамасынан келесі қасиеттер шығады:
1. Анықталмаған интегралдан алынған туынды интеграл астындағы функцияға, ал анықталмаған интегралдан алынған дифференциал интеграл астындағы өрнекке тең:
, ;
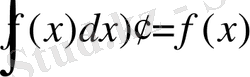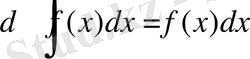2. Функция дифференциалынан алынған анықталмаған интеграл берілген функцияның өзі мен ерікті тұрақтының қосындысына тең:
;
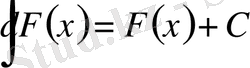3. Егер 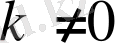- тұрақты сан болса, онда тұрақты көбейткішті интеграл таңбасының алдына шығаруға болады:
;
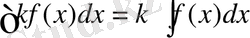4. Алгебралық қосындының анықталмаған интегралы жеке қосылғыштардан алынған интегралға тең:
;
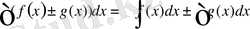5. Егер 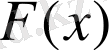функциясы 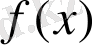функциясы үшін алғашқы функция, яғни 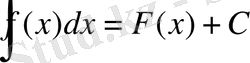, болса, онда
,
мұндағы және 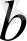- тұрақты сандар.

0.2 Интегралдаудың негізгі әдістері

Интегралдаудың негізгі әдістері бірнеше түрі бар, атап айтсақ тікелей интегралдау, айнымалыны алмастыру арқылы интегралдау, бөлiктеп интегралдау. Енді интегралдаудың әрбір әдісіне бекеше сипаттама бере кетейік.
Тікелей интегралдау әдiсi
Интеграл астындағы функцияны түрлендіріп, анықталмаған интегралдың қасиеттері мен интегралдар кестесін қолданып интегралдауды тікелей интегралдау әдісі деп атайды.
Айнымалыны ауыстыру әдісі
Интегралдағы х айнымалысының орнына жаңа t айнымалысын енгізіп, берілген 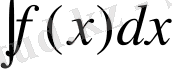интегралын тікелей интегралданатын кестелік интегралдардың біріне келтіруге болады. Бұл интегралдау әдісін айнымалыны ауыстыру әдісі деп атайды. Бұл әдістің негізі (3) күрделі функциялардың дифференциалдау формуласы болып табылады.
Теорема. Анықталмаған 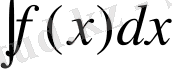интегралындағы х айнымалысының орнына 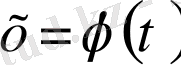формуласы бойынша жаңа t айнымалысын енгізсек, берілген анықталмаған интеграл үшін

(3)
теңдігі орындалады.
Есеп шығарғанда интегралдың жауабын бастапқы айнымалы арқылы жазу керек.
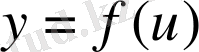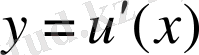Салдар. Айталық, және функциялары үзіліссіз болсын, онда (4) формула орындалады

. (4)

Дифференциал таңбасы астында кез келген функцияның алғашқы функциясына тұрақтыны қосып немесе алып пайдаланғаннан дифференциалдың мәні өзгермейді, яғни .
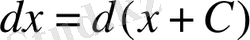Дифференциал мен интегралдың қасиеттерін пайдаланып интегралдауды дифференциал таңбасы астына енгізу әдісі деп атайды.
Бөліктеп интегралдау әдісі
Бөліктеп интегралдау әдісін қолданғанда интеграл астындағы өрнекті екі көбейткіштің көбейтіндісі түрінде қарастыру керек. Дифференциалдары үзіліссіз u=u(x) және v=v(x) функциялары берілсін.
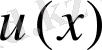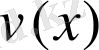Теорема. Егер және функциялары белгілі бір Х жиынында анықталған, дифференциалданатын және 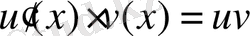функциясының осы аралықта алғашқы функциясы 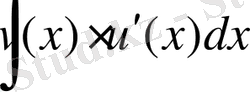интегралы болса, онда Х жиынында 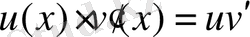функциясының да алғашқы функциясы 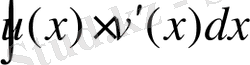интегралы бар болады, сонымен бірге 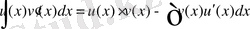немесе 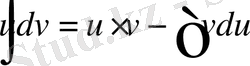(5)

(5)
теңдігі орындалады.
(5) - формула бөліктеп интегралдау формуласы деп аталады.
Көп жағдайда, бөліктеп интегралдау формуласын қолдану кезінде и(х)пен v'(x)dx=dv көбейтіндіcін дұрыс таңдау маңызды. Интеграл астындағы өрнек функциялардың көбейтінділерінен құралса, онда көбейткіштердің түріне қарап, үш топқа бөлуге болады.
Қарапайым рационал бөлшектерді интегралдау
Анықтама. 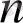- ші дәрежелі
,
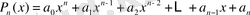Мұнда n - натурал сан, 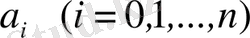- тұрақты коэффициенттер, алгебралық көпмүшені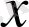аргументінен тәуелді бүтін рационал функция деп атайды.
Кез келген рационал функцияны екі көпмүшенің қатынасы түрінде жазуға болады (6) :
, (6)
мұнда 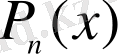- - 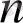ші дәрежелі, ал 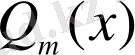- m - ші дәрежелі көпмүшеліктер. Егер бөлшектің алымында тұрған 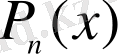көпмүшелігінің дәрежесі оның бөлімінде тұрған 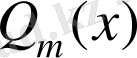көпмүшелігінің дәрежесінен кіші болса (яғни, мұндағы 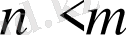), онда 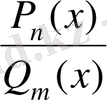бөлшекті дұрыс рационал бөлшек, ал, егер, керісінше, 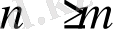болса, онда бөлшекті бұрыс рационал бөлшек деп атайды.
Кез келген 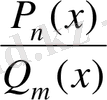бұрыс рационал бөлшекті алымын бөліміне бөлу арқылы оны көпмүшелік пен дұрыс рационал бөлшек қосындысы түрінде жазуға болады.
Рационал функцияларды интегралдау
Рационал функцияларды интегралдау мәселесі бізді дұрыс рационал бөлшекті интегралдауға әкеледі. Дұрыс рационал бөлшекті интегралдау үшін оны жәй бөлшектер қосындысына жіктеп алып, содан кейін интегралдаймыз.
Кейбір иррационал және тригонометриялық функцияларды интегралдау
Иррационал функцияларды интегралдау үшін айнымалыны ауыстыру әдісін қолданамыз.
1) түріндегі интеграл, мұндағы - аргументтері бойынша рационал функция және 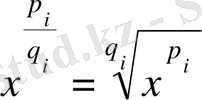түріндегі дәрежелік функциялар.
Берілген интегралда дәрежедегі 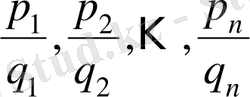бөлшектердің ең кіші ортақ бөлімін 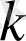арқылы белгілеп, 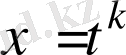, ауыстыруын қолданамыз. Соның нәтижесінде айнымалы бойынша жаңа рационал функцияның интегралын аламыз:

.
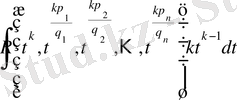2)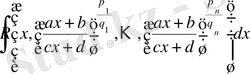түрдегі интеграл, мұндағы 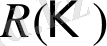- аргументтері бойынша рационал функция.
Берілген интегралды есептеу үшін ауыстыруын жасап, интегралды рационал функцияның интегралы түріне келтіреміз, мұндағ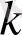ы саны 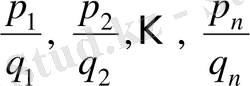бөлшектерінің ортақ бөлімі [4, 114].
Тригонометриялық өрнектерді интегралдау
1. 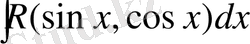түріндегі және функцияларынан тәуелді рационал функцияның интегралы.
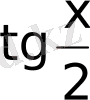
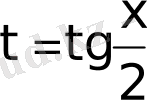Бұл түрде берілген интегралды есептеу үшін және функцияларын арқылы өрнектеп, ауыстыруын қолданып, интеграл астындағы өрнекті рационал бөлшекке келтіреміз, яғни мына формулаларды қолданамыз:

, ,
.

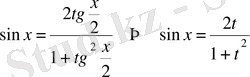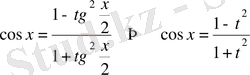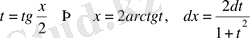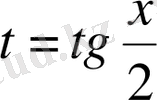-ауыстыруын әмбебап ауыстыру формуласыдепатайды.
Әмбебап ауыстыруды қолданғаннан кейін, берілген интеграл 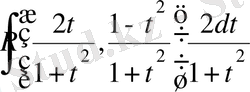рационал функцияның интегралы түрінде жазылады.
Көптеген жағдайларда тригонометриялық функцияның қасиеттерін ескеріп, басқа ауыстыруларды қолдану, бұл түрдегі интегралды есептеуді жеңілдетеді. Дербес жағдайларда ұтымды болатын тригонометриялық функцияларды интегралдау әдістерін қарастырайық.
а) Егер функциясы функциясына қатысты тақ болса, яғни 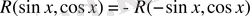теңдігі орындалса, онда 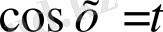ауыстыруын қолданамыз.
б) Егер 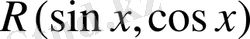функциясы 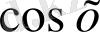функциясына қатысты тақ болса, яғни 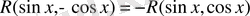теңдігі орындалса, онда 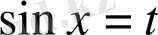ауыстыруын қолданамыз.
в) Егер 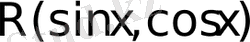функциясы және функциялары бойынша жұп болса, яғни 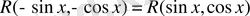теңдігі орындалса, онда 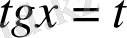ауыстыруын қолданамыз.
2. 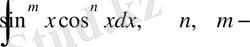бүтін нақты сандар 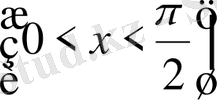түріндегі интегралдар.
а) Егер - жұп оң сандар болса, онда төмендегі формулаларды:

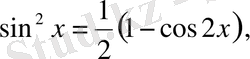
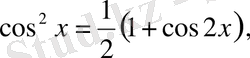
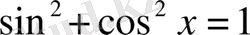
қолданып, интеграл астындағы функцияның дәрежесін төмендетіп, интегралдаймыз.
б) Егер 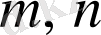- сандарының екеуі де тақ және ең болмағанда біреуі теріс болса, онда 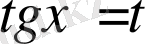немесе 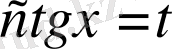ауыстыруларын қолданамыз.
в) Егер 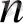- бүтін оң тақ сан болса, онда 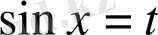ауыстыруын, ал егер - бүтін оң тақ сан болса, онда 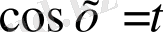ауыстыруын қолданамыз.
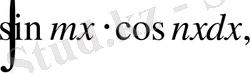
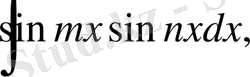
3. 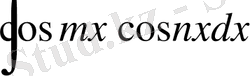түріндегі интегралдар.
Анықталған интегралда айнымалыны ауыстыру.
Теорема. Егер 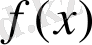функциясы 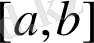кесіндісінде үзіліссіз, ал 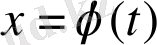функциясы 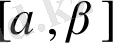кесіндісінде монотонды және үзіліссіз дифференциалданатын болса (мұндағы 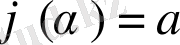, 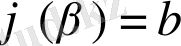), онда

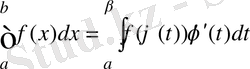
теңдігі орындалады. Бұл теңдік анықталған интегралда айнымалыны ауыстыру формуласы деп аталады.
Анықталған интегралды бөліктеп интегралдау.
Теорема. Егер u=u(x) және 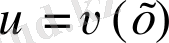функциялары 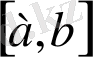кесіндісінде бірінші ретті туындыларымен бірге үзіліссіз болса, онда

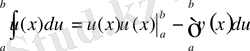
немесе
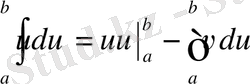
теңдігі орындалады. Бұл теңдік анықталған интегралды бөліктеп интегралдау формуласы деп аталады.
Тік бұрышты координаталардағы аудан
а) Егер 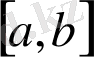кесіндісінде 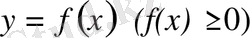болса, онда осы кесіндіде

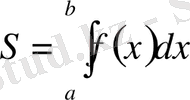
интегралы қисық сызықты трапецияның ауданын өрнектейді.
Ал, егер 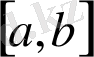кесіндісінде 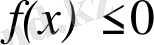болса, онда
.
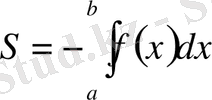б) Егер қисық сызықты трапеция төменнен және жоғарыдан сәйкес 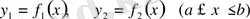функцияларының графиктерімен шектелген болса, онда ауданды мына формула бойынша есептейді:

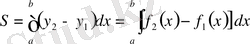
1.3 Күрделі интегралдарды жуықтап есептеу

Жуықтап интегралдау әдісі кез-келген үзіліссіз (функцияның анықталған интегралының жуық мәнін жеткілікті дәлдікпен табуға мүмкіндік береді. Кез-келген үзіліссіз функцияның алғашкы функциясы элементар функциялар арқылы өрнектеле бермейтіндігі осыдан. Анықталған интегралды жуықтап есептеу қажеттігі: интегралдың сол мәнін табу мүмкін емес немесе оны табу белгісіз жағдайларда да туады. Интегралдарды жуықтап есептеудің негізігі мәні ола интегралдың мәнін табу мүмкін емес немесе оны табу белгісіз жағдайда бөлшектей отырып нақты мәнге сәйкес нәтижені алу. Интегралды жуықтап есептеу әдісін түсіну үшін төмендегі есептерді қарастырамыз.
Есеп. Күрделі [a,b] кесіндісінде (a мен b-арқылы сандар) үзіліссіз f(x) = 0 функциясы берілсін (1-сурет). y=f(x) қисығы, Ох өсі және x=a мен x=b түзулерімен шенелген фигураның
y
0
x

y
0
x

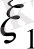
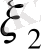
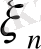
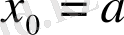
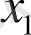
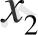
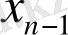
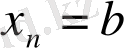
Cурет 1 y=f(x) қисығы.

1) S аудан ұғымын анықтау керек; 2) осы S ауданды табу керек.
Есептегі көрсетілген фигураны қисық сызықты трапеция дейді. Бұл есепті шығару үшін келесі амалды орындаймыз
а) 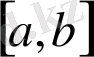кесіндіні кез-келген a=x0x1x2 ... .xn =b нүктелерімен n бөлікке бөлеміз.

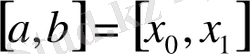
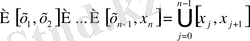және қисығының

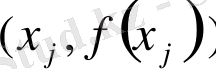
j=0,1,2 ... .,n нүктелерінің 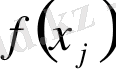ординаталарын тұрғызамыз;
б) әрбір 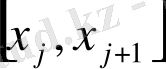бөлікше кесіндіден кез-келген нүктесін 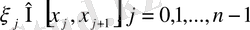аламыз және осы нүктелердегі 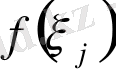функция мәндерін тауып, келесі қосындыны құрамыз
.
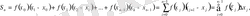
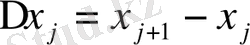Анықталған өрнек 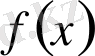функциясының 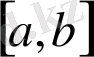кесіндідегі интегралдық қосындысы деп аталады. Оның әрбір 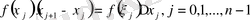қосылғышы - табаны 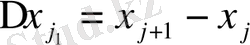, биіктігі 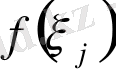болатын тік төрбұрыш ауданына тең, ал Snсаны қисықсызықты трапеция ауданын белгілі бір дәлдікпен жуықтайды: Sn ≈S . Бұл жуық теңдік дәлірек болуы үшін барлық 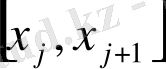, j=0,1,2 ... .,n-1 , бөлікше кесінділеді мейлінше ұсақтай түсу керек екені түсінікті;
в) ұзындығы ең үлкен бөлікше кесіндіні нөлге ұмтылдырамыз
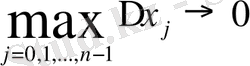
Егерде осыдан Sn шамасы кесіндісін бөлу тәсіліне және жәбір бөлікше кесінділерден алынған 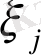нүктелерін таңдау тәсілдеріне тәуелсіз S нақты санына ұмтылса, онда S саны қисықсызықты трапецияның ауданы (12) деп аталады

(12)

Сонымен, І-есептің екі сұрағына да жауап алдық.
ІІ-есеп. Х өсіндегі 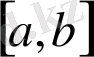кесіндісінде жатқан сызықтық біртексіз стержень (желі) берілсін. Оның массасының үлестіру тығыздығы ρ(x) - үзіліссіз функция болсын. Осы стерженнің массасын анықтау керек.
А)стерженді кез-келген a=x0x1...,xn =b нүктелермен n бөлікке бөліктейміз:;
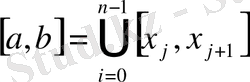Б) әрбір 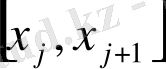бөліктен кез-келген 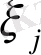нүктесін 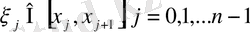алып, келесі интегралдық қосындысын құраймыз:
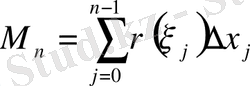
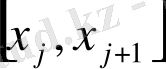Аралығында ρ(x) функцияның өзгеруі шамалы болғандықтан, стерженнің 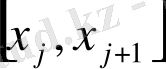кесіндісіне сәйкес келетін бөлігінің массасының жуық мәні 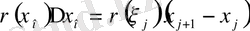тең болғандықтан, қосындысы Mn бүкіл стерженнің массасын жуықтайды;
В)стерженнің массасының дәл мәнін, ұзындығын ең үлкен бөлікше кесіндіні нөлге ұмтылдыра отырып, Mn интегралдық қосындының шегіне өту арқылы аламыз:

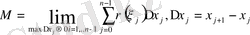
Осы сияқты f күшінің әсерінен дененің түзу сызықпен аралығындағы қозғалысының A жұмысын анықтауға болады:

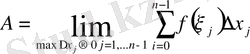
тағы да басқа көптеген физикалық есептерді осылай шешуге болады.
Бұл есептер бізді 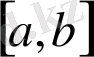кесіндісінде берілген, тегі әртүрлі функцияларға жасалатын бір ғана математиокалық амалға алып келіп отыр. Бұл амал-функцияны кесіндіде интегралдау деп, ал оның нәтижесі - функцияның кесіндідегі анықталған интегралы деп аталады.
Анықтама. 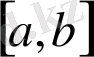kесіндісінде y=f(x) функциясы берілсін.
А) 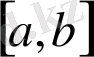кесіндісін кез-келген a=x0x1...,xn =b нүктелермен 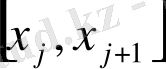, i=0,1...n-1, бөліктерге бөлеміз.
Б) әрбір 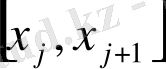бөліктен кез-келген 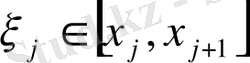нүктелерін алып, f функциясының R - бөліктеуіне сәйкес интегралдық қосынды деп аталатын
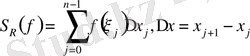
Қосындысын қарастырамыз;
В) 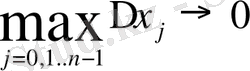ұмтылдырып интегралдық қосындының шегін аламыз.
Егер бұл шек бар болса, онда ол f функцияның 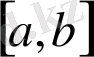кесіндісіндегі анықталған интегралы деп аталады да 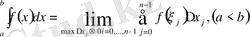түрінде беріленеді. Мұндағы a мен b сандары - анықталдған интегралдың сәкес төменгі және жоғарғы шегі деп аталады.
Функцияны интегралдаудың сандық әдістері анықталған интегралдың геометриялық берілуіне, яғни y=f(x) функция графигі абсцисса өсімен және x=a, x=b екі түзуімен шектелген қисық сызықты трапеция ауданына (13) негізделеді (2-сурет):

(13)
. x=a
x=b
y=f(x)
y
x
y0

y1
yn-1
yn
x=a
x=b
y=f(x)
y
x
y0

y1
yn-1
yn
Cурет 2 Қисық сызықты трапеция.
Жоғарыдағы қисық сызықты трапецияның ауданын есептеу үшін оларды бірнеше элементар ауданға (қисық сызықты трапеция, трапеция және тікбұрыш) бөлеміз.
Тік төртбұрыштардың және трапециялардың квадратуралық формулалары.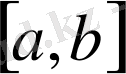кесіндісін ах0х1х2...хnb нүктелерімен әрқайсысының ұзындығы х болатын өзара тең n бөлікке бөлеміз (14). Онда

х. (14)

Ал х0,х1,...,хn нүктелеріне сәйкес келетін f(x) фунуциясының мәндерін сәйкес у0,у1,...,уn деп белгілейміз, яғни у0f(x0), y1=f(x1), ... , yn=f(xn) онда
=y0x+y1x+...+уn-1x. =y1x+y2x+...+уnx қосындылары (х) функциясының а,b кесіндісіндегі интегралдық қосынды болады да, олар интегралдардың жуық мәнін береді және (15) мен (16) теңдіктері тік төртбұрыштардың квадратуралық формулалары деп аталады.

, (15)

, (16)

Жуықтап есептеу нәтижесі дәлірек болуы үшін бөлікше аралықтар санын көбірек, яғни адымын кішірек етіп алу керек.
а,b кесіндісін бөліктеуді сол күйінде қалдырамыз, бірақ у=f(x) сызығының әрбір бөлікше аралыққа сәйкес келетін доғасын, осы доғалардың ұштарын қосатын хордалармен алмастырамыз. Басқаша айтқанда, берілген қисық сызықты трапецияның орнына n тік бұрышты трапецияларды аламыз. Мұндай фигура ауданы тік төртбұрыштардан құралған n баспалдақты фигура ауданына қарағанда ізделініп отырған ауданды дәлірек өрнектейтінін геометриялық тұрғыдан-ақ көруге болады (3,4-суреттер).

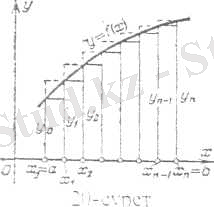
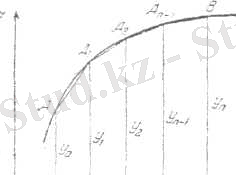
3-cурет қисық сызықты трапециялар 4-сурет n тік бұрышты трапециялар

Алынған әрбір тік төртбұрышты трапеция ауданы , i=0,1,...,n-1, болғандықтан

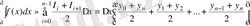
немесе. (17)

(17) жуық теңдік трапециялардың квадратуралық формуласы деп аталады.
Егер функция (х)Ах+В - сызықтық болса, онда (1)-(3) жуық теңдіктері дәл теңдікке айналады.
Егер функциясының (х)М1 теңсіздігін қанағаттандыратын құрақты - тегіс туындысы бар болса, онда (18) (19) тік төртбұрыштар формуласының қалдық мүшесі

, (18)

және трапециялар формуласының формуласының қалдық мүшесі

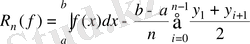
үшін

(19)

теңсіздігі орындалады.
Мұндағы константаларды азайта алмаймыз, олар дәл есептелген..
[а.Ь] кссіндісінде екінші туындысы шенелген функциялар класы үшін тік төртбүрыштар мен трапециялар формулаларының қалдық мүшелері

(20)

теңсіздігін қанағаттандырады, яғни мұнда (19)-(20) формулалар арқылы жуыктау реті болады.
Ал шенелген үшінші, төртінші т.с.с. жоғарғы туындылары бар функциялар класстары үшін (19)-(20) формулалардың жуықтау реті жақсармайды (артпайды), яғни жуықтау реті болып қала береді .
Бұл құбылыс (17)-(19) формулалардың бірінші дәрежелі көпмүшеліктер үшін дәл, ал дәрежесі бірден жоғары көпмүшеліктер үшін дәл еместігімен тығыз байланысты.
Енді (19) теңсіздіктің дәлелдеуін келтірейік.
Сонымен, f(x) функциясының құрақты-тегістуындысы [а,Ь] кесіндісінде (4) шартты қанағаттандырсын. Егер h=, , k=0,1,...,n-1 деп белгілесек, онда [a,b]=,
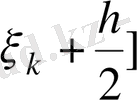
болады да

Осыған Лагранж теоремасын қолданып, (20) шарт бойынша

аламыз.
Симпсон формуласы. [а,b] кесіндісін саны жұп п = 2т өзара тең дербес бөліктерге бөлшектейміз. у(х)сызығының [хк,хк+2] к=0,1,...,п-2,аралығындағы доғасын Мк(хк,ук),Мк+1(хк+1,ук+1), Мк+2(хк+2,ук+2) үш нүкте аркылыөтетін осі Оу -ке параллель у=Ах2+Вх+С екінші дәрежелі парабола доғасымен алмастырамыз .
Мұндағы А,В,Скоэффициенттері параболаның берілген үш нүкте арқылы өту шартынан табылады. Осылай алынған параболалық трапециялардың аудандарының қосындысы интегралдың жуықмәнін береді.
Мысал. 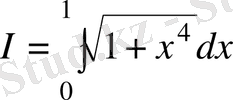интегралын жуықтап есептеукерек.
Бұл интеграл элементар функциялар арқылы алынбайды. Оны жуықтап есептейміз, ол үшін [0,1] кесіндісін өзара тең 10 бөлікке бөлеміз: х0=0,2,...,х9=0,9, х10=1.
Осы нүктелердегі (х) = 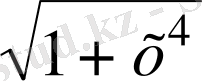функциясының мәнерін
(0) = 1, (0.1) = 1,00005, (0,2) = 1,00080, (0.3) = 1.00404,
(0.4) = 1,01272, (0,5) = 1,03078. (0,6) = 1,06283, (0,7) = 1,11360,
(0,8) = 1,18727,(0,9) = 1,28690, (1) = 1,1421
табамыз.
Трапециялардың квадратуралық формуласы бойынша ((17) формула)

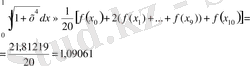
аламыз.
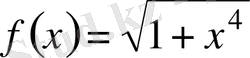функциясының [0,1] кесіндісінде кез келген үзіліссіз туындысы бар. Бірақ трапецния формуласының қателігін екінші үзіліссіз туындыға қарап анықтаймыз. Өйткені бұл формуланың қателігіне функциянын екіден үлкен үзіліссіз туындыларының бар болуының әсері
жоқ.Сонымен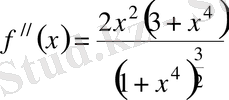және М2=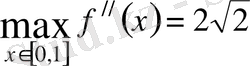. Демек, трапеция формуласының қалдық мүшесі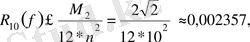яғни
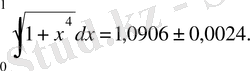
Тік бұрыштар, трапециялар және Симпсон формулаларын қолданып 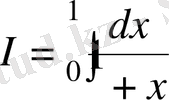интегралын жуықтап есептеп, шыққан нәтижелерді Ньютон - Лейбниц формуласы бойынша бірден табылатын дәл мәнімен салыстыру керек:

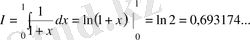
Шешу. 1) Әуелі интегралдың жуық мәнін ( тік бұрыштар формуласы

немесе

бойынша табайық.
[0,1] аралығын нүктелер х0=0; х1=0,1; х2=0,2; ...,х9=0,9, х10=1-лермен тең оң бөлікке бөліктейміз. Сонда
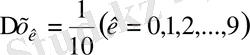. Функция 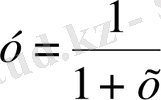-тің осы нүктелердегі мәндерін табамыз.
Бұл мәндерді сәйкесінше у0, у1, у2,..., у10 деп белгілейміз. Бұл ординаталарды үтірден кейінгі үш таңбасымен, әрі 0,0005-ке дейінгі дәлдікпен есептейміз, яғни: у0=1,000; у1=0,909; у2=0,833; у3=0,769; у4=0,714;
у5=0,667; у6=0,625; у7=0,588; у8=0,556; у9=0,526; у10=0,500. (29) және (30) формулаларды n10 болған жағдайында қолданып, мынаны табамыз:

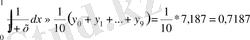
Немесе

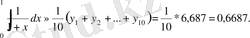
Мұнан бұл мәндердің дәл мәннен айырмасы 0,03 тең кем болатынын көреміз.
2) Сол интегралдың жуық мәнән трапециялар формуласы

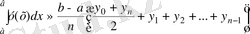бойынша табайық.

Бірінші жағдайдағыдай мұнда да 0,1 аралығын (*) нүктелерімен тең он бөлікке бөліктейміз де, сол нүктелерге сәйкес ординаталарды үтірден кейін төрт таңбасы бар бөлшектер түрінде табамыз. Олар: у0=1,0000; у1=0,9091;у2=0,8333; у3=0,7692; у4=0,7143; у5=0,6667; у6=0,6250; у7=0,5882; у8=0,5556; у9=0,5263; у10=0,5000. Сонда n10 болған жағдайда трапециялар формуласы мына нәтижені береді:

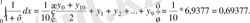
Мұнда тек үш таңба ғана дұрыс, ал алынған нәтиже дәл нәтижеден шамамен алғанда 0,0006-ға ғана айырылады. Мұнан шыққан нәтиже бұдан бұрынғы тікбұрыштар формуласы бойынша алынған нәтижеден анағұрлым жақсы екенін көреміз.
3) Енді сол интегралдың жуық мәнін Сипсонның

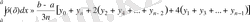
формуласы (мұндағы n жұп сан) бойынша табалық.
Бұл жағдайда 0,1 аралығын тең төрт бөлікке

нүктелерімен бөліктейміз. Оларға сәйкес ординаталарды үтірден кейін төрт таңбасы бар бөлшектер түрінде табамыз, яғни: у0=1,0000; у1=0,8000; у2=0,6667; у3=0,5714; у4=0,5000. Сонда n4 болғанда Симпсон формуласы мына нәтижені береді:

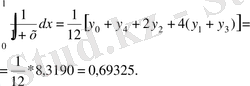
Бұдан үш таңбаның дұрыстығын және шыққан нәтиженің дәл нәтижеден айырмасы шамамен 0,0001 болатынын көреміз [14].

2 Интегралдарды жуықтап есептеудің әдістері

2.1 Тікбұрыштар әдісі

Тікбұрыштар әдісі қисық сызықтың көлемін білдіретін, олардың нәтижесі нақты бір интегралдың геометриялық мағынасын қолдануында негізделеді. Кейбір қосымша ұсыныстардан құралған, тікбұрыштардың формуласын интегралдық қосынды деуге болады.
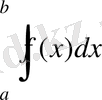интегралын шығару керек делік, интегралдаудың үзіндісін n бірдей бөліктерге бөліп және функция мағыналары интегралдың қосындысына кіретін, нүктелері алынған үзінділердің сол жақтарына жайғастырамыз. Егер n-ді үлкенірек деп есептесек, демек h=(b-a)n бөліктердің үзінділердің ұзындығы кішірек болады, интегралдық қосынды интегралдың мөлшерінен айырмашылығы болмау керек. Сонымен қатар мынадай (26) жуық теңдеулер аламыз:

(26 )

Мұнда теріс тікбұрыштардың формуласы деп аталады. Осы жерде бұрынғыдай у0,у1,у2, ... уn арқылы х0,х1,х2,...хn бөлулердің нүктелерінде y=f(x) функцияның мағыналары белгіленген. Тікбұрыштардың ұқсас формуласы былай да шығарылады: егер интегралдық қосындының функция мағыналарын теріс жақта емес, керісінше, бөлулердің оң жақтан алатын болсақ, сол кезде формула (27) болады:

(27)

Функция үшін, әр интегралдың қосындысы нақты интегралдың (26) және (27) формулалардың оң жақтарында көрсетілген. Жуықталған мағыналардың арасында қосылған (5-сурет).
y0
yn
x
y
0
a
b
y0
yn
x
y
0
a
b

Cурет 5 Геометриялық көркемдеуі.

Осы жерден әр түрлі қосындыға кіретін, көбеюші функцияны және қосылғандарды алу, пункттер және штрих түсірумен көрстілген.
Осыған орай тікбұрыштардың формулаларының қателіктері туралы көріністі, (26) және (27) формулалары бойынша алынған айырымның нәтижелерін қарастыра білуге болады.
Егер функция интегралдаудың үзіндісінде ақырғы түрде табылатын экстримумдардың санын иеленсе, интегралдаудың үзінділерін бірқалыптылық бөліктерін бөлуге болады. Осылайша тікбұраштар формулаларының қателіктеріне бағалады.

2.2 Трапеция әдісі

Тіктөртбұрыштардың формуласымен алынған арифметикалық ортасының жуығы қандай да мәнге тең, демек интеграл мағынасының түп мәніне тең болып шығады: қателік 0,05% -ке тең. (26) және (27) формулалары бойынша алынған, интегралдаудың жуықталған мағынасы ретінде орташа арифметикалықтың жуықтаын алуға тура келеді.
Байқасақ, бұл мағыналарды алдын ала шығарып қоюды еш мұхтаждығы жоқ. Өйткені бірден дайын формуламен пайдаланса болады. Шынымен де, (26) және (27) оң формулаларының арифметикалықтың ортасын алсақ, (28) формуланы аламыз:

(28)

бұл трапециялар формуласы.
(28) трапециялар формуласын былайша оңай алуға да болады, геометриялық мағынасынан шыға тура, a=x0x1x2...xn-1xn=b нүктелермен интегралдаудың үзіндісін n-бірдей бөлікке бөліп, бөлулердің барлық нүктелердің ординаталарды жүргіземіз және әр алынған қисық сызықтытыны түзу сызықтыға ауыстырамыз, төмендегі суретте көрсетілген. Әр трапецияның жақтары екі көрші ординаттар болып табылады. 6-суретте Ох сызбаның аймағы берілген, ұзындығы h=(b-a)n және хордасы қисық.
0
y
x
y0
x0
yn-1
xn-1
yn
xn
y1
x1
0
y
x
y0
x0
yn-1
xn-1
yn
xn
y1
x1
Cурет 6 Қисық трапеция.

Сол трапецияның көлемі (хі-1,хі) аймақтың үстінде орналасқан, трапецияға сай, мынаны табамыз.

(29)

1-ден n-ге дейін барлық і-ға (29) көрсетілімдерді қосу, өйткені шеттегіден басқа барлық ординаттар, (29) көрсетілімдердің түрінде екі мәрте қолданылады.
Трапециялық тәсілмен жасалатын сандық интегралдау
Электрондық есептеу машинасындағы сандық интегралдау тәсілдерді іске асыруды қажет ететін, нақты бір интегралдың мысалдарын келтірейік.
Мысалы, егерде f(x)-электростанцияға ауырлық болса, квт-уақытта (х-тәуліктің басынан есептелетін, уақыттың саны), тәуліктің ішінде электірлік энергиялық шығыны құрайтын (30) формула:

(30)
немесе басқа мысал:
t-уақытта алынған, дисконтталған кірістің көлемі (31) формулаға тең:
(31)
Мұндағы:
t-уақыт
і-пайыздың меншікті нормасы (пайыздар үздіксіз өсе береді) және трапециялық тәсілді қолданамыз.
Тәсілдің мәні: интегралдаудың арасы [a, b] n нүктелермен бірнешеге бөлінеді. (n+1) бірдей кішкентай бөліктерге.
(32) трапеция формуласының көрінісі:
(32)

f(x) - интегралдың астындағы функциясы;
a, b ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.