Мәтінді есептерді геометриялық әдістермен шешу

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ОҚУ-АҒАРТУ МИНИСТРЛІГІ ШЫҒЫС ҚАЗАҚСТАН ОБЛЫСЫ
ДАРЫНДЫ БАЛАЛАРҒА АРНАЛҒАН ЖАМБЫЛ АТЫНДАҒЫ ОБЛЫСТЫҚ МАМАНДАНДЫРЫЛҒАН
МЕКТЕП-ГИМНАЗИЯ-ИНТЕРНАТЫ

Бағыты: Экономикалық және әлеуметтік үрдістерді математикалық модельдеу
Секциясы: Математика
Тақырыбы: Мәтінді есептерді геометриялық әдістермен шешу

Орындаған: Солтанбеков Фархат 10 сынып оқушысы
Ғылыми жетекшісі: Аменова Ф.С. С.Аманжолов атындағы ШҚУ,
математика кафедрасының доценті, PhD докторы.
Пән жетекшісі: Мамыр Наурызбек Математика пәнінің мұғалімі.

Өскемен 2022 жыл

Мазмұны

Кіріспе ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙
3
Негізгі бөлім

І. Қозғалысқа берілген есептерді геометриялық жолмен шығару ∙∙∙∙∙
5
1.1 Қозғалыстың негізгі түрлеріне анықтама ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙
5
1.2 Қозғалысқа байланысты есептердің геометриялық модульдері ∙∙∙∙∙∙∙∙∙
6
II. Жұмысқа байланысты есептерді геометриялық
жолмен шығару ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙

11
2.1 Жұмысқа байланысты есептерге мысалдар арқылы
сипаттама жасау ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙

11
ІІІ. Концентрацияға, қоспаға берілген мәтіндік есептерді
геометриялық жолмен шығару∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

16
3.1 Концентрацияға берілген есептердің негізгі компаненттері ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
16
3.2 Қоспаға байланысты есептерді шығарудағы
геометриялық әдістер ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙

17
Қорытынды ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
20
Әдебиетттер тізімі ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
20

"Мәтіндік есептерді геометриялық әдіспен шығару"
ЭССЕ

Мәтіндік есептерді шешудің әртүрлі тәсілдері қарастырылады. Оқушыларды шығармашылыққа баулитын, математикалық білімді саналы түрде игеруге мүмкіндік беретін тәсілдер көбірек маңызға ие болуда.Шығармашылық ойлау қабілетінің және оқу материалын формальды емес игерудің бірден бір көрсеткіші ақпараттың берілуін геометриялық түрде қолдана білу болып табылады. Осы қолданысты білу, әсіресе, алгебралық (мәтіндік) есептерді шешуде маңызды орын алады, өйткені ол қиял мен ойлау қабілетін ұштастыруға мүмкіндік береді.

Берілген жобада қозғалысқа, жұмысқа және концентрацияға берілген мәтіндік есептерді геометриялық жолмен шығарылуына мысалдар келтірілген. Бұл мысалдарды шешуде геометриялық фигуралар мен графиктерді қолданған. Мәтіндік есептердің негізгі түрлерін ажыратып, оларға жеке сипаттама бердім. Қозғалысқа берілген есептерді талдау барысында тіктөртбұрыш қасиеттеріне сүйендім.

Ғылыми жобаны қорытындылай келсек, бұл ғылыми жобада жалпы үш бөлімді қарастырдық. Олар: қозғалысқа, жұмысқа және концентрацияға байланысты алгебралық мәтінді есептерді геометриялық жолмен шығару. Алгебралық мәтінді есептерді геометриялық әдіспен шешу есептің шартын көрнекі түрде бейнелеуге мүмкіндік береді. Кейде есептерді аналитикалық есептеулер жасамай-ақ, есептің схемалық моделін құрастыру арқылы да шешуге болады. Бұл оқушылардың ойлау қабілетін жақсартады. Кейбір оқушылар мәтінді есептерді тек қана алгебралық әдіспен шығара алады. Оның басқа жолдарын шығара білгеннің өзімізге пайдасы тиеді. Сондықтан да біз жобада оқушыларды алгебралық мәтінді есептерді геометриялық жолмен шығаруға үйретіп тұрмыз.

Аннотация
Мектеп математика курсында оқушылар әдетте мәтінді есептерді арифметикалық және алгебралық әдістермен шешуге дағдыланады. Алгебра курсында геометриялық әдіс әртүрлі есептердің қосымша моделін құруда немесе көрсетуде пайдаланғанымен, нақты түрде қарастырылмайды. Бұл ғылыми жобада алгебралық мәтінді есептерді геометриялық әдістермен шешу ұғымына анықтама беріліп, нақты мысалдармен оқушыларды мәтінді есептерді геометриялық әдіспен шешуге үйрету тәсілдері көрсетілген.
Тірек сөздер: алгебралық мәтінді есептер, геометриялық әдіс, геометриялық фигуралар, геометриялық қатынастар, графикалық әдіс, сызықтық функцияның графигі.

Annotation
Usually, in a school mathematics course, students develop skills in solving text problems in arithmetic and algebraic ways. In the course of algebra, the geometric method is used to construct or image additional models. The article defines the concept of "geometric method for solving algebraic problems." In this research project show the use of the geometric method for solving algebraic text problems.
Keywords: algebraic text problems, geometric method, geometric figures, geometric relationships, graphical method, graph of a linear function.

Кіріспе
Жобаның жалпы сипаттамасы. Бұл жобада біз негізгі мәтіндік есептерді геометриялық жолмен өрнектеп, шығар амыз. Мәтіндік есептерге анықтама береміз. Оның әрбір түріне сипаттама беріп, мысалдар қарастырамыз. Осы мысалдардың шартына сәйкес геометриялық моделін құрып, оны есеп шығаруда пайдаланамыз. Қазіргі таңда жаңартылған білім беру мазмұнында біздің тұлға ретінде дамуымызға база назар аударып отыр. Осыған орай, бізге мұғалімдер математикалық білім берген кезде алгебралық тәсілден бөлек жаңа тәсілдерді тиімді пайдалануымыз қажет. Жаңа тәсілдер біздің ой өрісімізді дамытуымызға, өз бетімізше жаңалықтар ашуымызға, о ларды дәлелдеуімізге, есептерді шығаруымызға және т.б. амалдарды үйреніп алуымызға бағытталған. Оқушыларды жаңашылдыққа үйретудің бірден-бір жолы - мәтінді есептерді шешумен тығыз байланысты. Математиканы оқытуда іс-әрекеттік тәсілдің мақсаттары: есепті шығару және есептің шешімін іздестіру амалын, оның әртүрлі әдістерін игеру. Осыған байланысты мұғалімдердің математика курсынан есептерді шешудің, оның ішінде мәтінді есептерді шешудің әртүрлі тәсілдерін меңгеруі тиіс деп білеміз [1]. Зерттеу өзектілігі. Мектеп жасында ғылар мәтіндік есептерді шешуде геометриялық әдістерді қолданбайды. Сол себептен, біз осы ғылыми жұмыста алгебралық мәтінді есептерді гео метриялық жолмен модельдеудің ерекш е әдістерін ұсынбақшымыз. Алгебралық мәтінді есептер шешуде геометриялық әдістерді қолдану математиканы оқып-тануда тұлғалық іс-әрекеттік тәсілдерді жүзеге асыруға мүмкіндіктер береді . Сонымен қоса, есептер шығаруда геометриялық әдістерді пайдалану балалардың шығармашылық ойлау қабілетін дамытуға ықпал етеді. Яғни, біздің шығармашылық ойлау дәрежеміздің көрсеткіштерінің бірі - берілген ақпаратты геометриялық біліміміз арқылы талдау жасап көрсете алуымыз. Әсіресе, алгебралық мәтінді есептерді шешуде балалардың геометриялық әдістерді пайдалануы олардың логикасы мен елестету
қабілетін терең байланыстырады.
Жобаның мақсаты мен міндеті. Бұл жұмыстың негізгі мақсаты-әр түрлі кейіпте берілген мәтіндік есептерді геометриялық моделін жасау арқылы шығару. Геометрияның негізгі компаненттерін (фигуралар, диаграммалар, сызбалар және т.б.) есеп шығарғанда дұрыс қолдана білу.
Осы мақсатқа жету үшін біз алдымызға бірталай міндеттерді қойдық:
-Мәтіндік есептер ұғымының не екенін анықтау;
-Мәтін есептердің түрлерін анықтап, оларға анықтама беру;
-Әрбір түрге мысалдар қарастырып, геометриялық модельденген шешімін
табу.
Зерттеу нысаны. Қозғалысқа, жұмысқа және концентрацияға берілген
есептер.
Зерттеу әдістері. Анықтау, есептеу, салыстыру, жинақтау, дәлелдеу, талқылау, жүйелеу.
Зерттеу жаңалығы. Бұл жобаның басты жаңалығы-алгебралық мәтіндік есептерді геометриялық жолмен өрнектеу. Математикадан бөлек физика және химия саласында кездесетін мәтіндік есептерді геометриялық фигуралармен немесе диаграммалар арқылы шығару.

Геометриялық әдіс Евклидтің (б.з.д. ІІІ ғ.) заманында пайда болып, тек геометрияда ғана емес алгебрада да пайдаланған. Ол кезде алгебралық есептерді шешудің ерекшелігі: есепті тек қана салулар мен геометриялық заңдылықтар арқылы шешу қарастырылған, аналитикалық тәсілдер қолданылмаған. Осыдан геометриялық алгебра дамыған [2].
Біз алгебралық мәтінді есептерді геометриялық әдіспен шешу деп геометриялық фигуралар (нүкте, кесінді, үшбұрыш, тіктөртбұрыш және т.б.) мен олардың қасиеттерін, геометриялық қатынастар (теңдік, ұқсастық, теңшамалы және т.б.), геометриялық шамалар (ұзындық, аудан) мен аналитикалық әдістердің элементтерін (теңдеулер, арифметикалық өрнектер және т.б.) қолданып шешуді айтамыз. Алгебралық мәтінді есептің шартын геометриялық тұрғыда беруді осы есептің геометриялық моделі деп түсінеміз.
Сонымен, алгебралық мәтінді есептерді геометриялық әдіспен шешу келесі кезеңдермен жүзеге асады: 1) есептің геометриялық моделін салу, яғни есептің шартын геометриялық тілге аудару; 2) алынған геометриялық есепті шығару; 3) табылған жауапты геометриялық тілден табиғи (бастапқы) тілге аудару [3].
Енді осы кезеңдердің жүзеге асуын алгебралық мәтінді есептерді, оның ішінде қозғалысқа арналған мәтінді есептерді геометриялық әдіспен шешуді қарастырамыз.

І.Қозғалысқа берілген есептерді геометриялық жолмен шығару
0.1 Қозғалыстың негізгі түрлеріне анықтама

Қозғалысқа арналған есептердің негізгі түрлері: 1) түзу сызықты жолдың бойымен қозғалысқа арналған есептер: бір нүктеден бір бағыттағы, екі нүктеден бір-біріне қарама-қарсы бағыттағы қозғалыстар; 2) шеңбер бойымен қозғалысқа арналған есептер; 3) судың бойымен қозғалысқа арналған есептер [4].
Түзу сызықты жолдың бойымен қозғалысқа берілген мәтіндік есептерді шығарудың негізгі формуласы:

𝑺 = 𝑽 ∙ 𝒕
S-қашықтық; v-жылдамдық; t-уақыт.

ҚАШЫҚТЫҚ-белгілі бір уақыт көлемінде белгіленген жылдамдықпен жүріп өтілген жол. Ол ұзындықтың өлшем бірліктерімен белгіленеді.
ЖЫЛДАМДЫҚ-жүріп өткен жолдың уақытқа қатынасын сипаттайтын шама. УАҚЫТ-сол қашықтықты жүріп өтуге кеткен мезгіл.
Шеңбер бойымен қозғалысқа берілген есептерді шығарудың формуласы:

𝑣 =
2𝜋𝑅
𝑇 = 𝜔𝑅

𝑣 − сызықтық жылдамдық; 2𝜋𝑅 − шеңбер ұзындығы; 𝑇 − период, уақыт;
𝜔 − бұрыштық жылдамдық; 𝑅 − радиус.

Шеңбер бойымен қозғалыс көбіне физикалық есептерде келеді. Мұндай кейіптегі қозғалыстарда жылдамдықтың 2 түрі болады: 1) сызықтық жылдамдық;
2) бұрыштық жылдамдық.
Сызықтықтық жылдамдық деп-шеңбер ұзындығының периодқа, яғни уақытқа қатынасын айтамыз. Ал бұрыштық жылдамдық деп-сызықтық жылдамдықтың радиусқа қатынасын айтамыз.
Өзен бойымен қозғалысқа берілген есепттерді шығару формуласы:

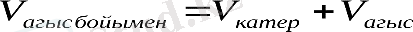
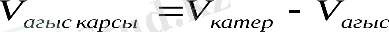
Егер катер өзенде ағыспен қозғалып отырар болса, онда катердің меншікті жылдамдығына ағыс жылдамдығы қосылады. Ал егер катер ағысқа қарсы жүзер болса, оның меншікті жылдамдығынан ағыс жылдамдығын азайтамыз. Сол себепті ағыс арқылы қозғалған дененің жүзу уақыты ағысқа қарсы жүзген дененің уақытынан аз болады.

2.1 Қозғалысқа байланысты есептердің геометриялық модульдері

1- мысал. Пойыз 720 км жолда 1 сағат кешігуін жою үшін кесте бойынша жүру жылдамдығын 10 кмсағ-қа арттырды. Пойыздың кесте бойынша жүру жылдамдығын табыңдар.
Шешуі. 1-тәсіл. Алгебралық әдіспен есепті шешу мынадай теңдеуді

құрастыру арқылы іске асады: [720] − 720
= 1, мұндағы x (кмсағ) - пойыздың кесте

бойынша жылдамдығы.
𝑥 𝑥+10

2- тәсіл. Геометриялық әдіс (1-сурет). Есептің шарты бойынша қозғалыс бірқалыпты болғандықтан, пойыздың жүрген жолы оның жылдамдығы мен уақытының көбейтіндісіне тең болады. Сондықтан оны тіктөртбұрыш ретінде қарастырып, оның қабырғалары ретінде пойыздың жылдамдығы мен уақытын аламыз.
ABCD тіктөртбұрышын салайық. AD = x - пойыздың кесте бойынша жылдамдығы (кмсағ), AB - пойыздың кесте бойынша жүру уақыты (сағ) болсын. Сонда,

𝑆𝐴𝐵𝐶𝐷 = 𝐴𝐵 ∙ 𝐴𝐷 = 720.

1-сурет 2-сурет

Пойыз жылдамдығын 10 кмсағ-қа арттырғандықтан AD кесіндісінен шартты түрде 10 кмсағ-ты кескіндейтін DG кесіндісін қосамыз. Арттырылған жылдамдықпен пойыз 1 сағ жылдамырақ жүргендіктен AB кесіндісінен шартты түрде 1 сағ-ты кескіндейтін BE кесіндісін алып тастаймыз. Пойыздың жүрген жолдары бірдей болғандықтан, ABCD және AEFG тіктөртбұрыштарының аудандары тең болады, яғни 𝑆𝐴𝐸𝐹𝐺 = 𝑆𝐴𝐵𝐶𝐷 = 720.
Сызбада 𝐴𝐵𝐶𝐷 және 𝐴𝐸𝐹𝐺 тіктөртбұрыштарының теңшамалы екенін
көрсету үшін теорема бойынша 𝐶𝐹 ∥ 𝐸𝐷 жүргіземіз.

𝑆1 = 𝑆2 болады, өйткені 𝑆𝐸𝐵𝐶𝐻 + 𝑆𝐴𝐸𝐻𝐷 = 𝑆𝐷𝐻𝐹𝐺 + 𝑆𝐴𝐸𝐻𝐷 .
𝑆 = 𝐵𝐸 𝐸𝐻 = 1 𝑥 = 𝑥, ал 𝑆 = 𝐷𝐺 𝐺𝐹 = 10 𝐺𝐹, 𝐺𝐹 = 𝑆𝐴𝐸𝐹𝐺 = 720 .

1 2 𝐴𝐺
𝑥+10

𝑆1 = 𝑆2 болғандықтан, келесі теңдеуді аламыз:

𝑥 = 10 [720] , 𝑥[2] + 10𝑥 − 7200 = 0.
𝑥+10

Осы теңдеуді шешіп, оның түбірлерін табамыз: 𝑥1 = 80, 𝑥2 = −90. Сонымен, пойыздың кесте бойынша жылдамдығы 80 кмсағ-қа тең болады.
Бұл есепте 1-суреттегі геометриялық қатынастарды (теңшамалы тіктөртбұрыштар, кесінділердің ұзындықтарының теңсіздігі, үшбұрыштардың ұқсастығы және т.б.) пайдалана отырып, әртүрлі теңдеулерді құрастыруға болады.

Мысалы, AB - AE = 1, ал 𝐴𝐵 = 720, 𝐴𝐸 = 𝐺𝐹 = 720 . Осыдан: [720] − 720
= 1.

𝑥 𝑥+10 𝑥 𝑥+10
𝑆𝐴𝐵𝐶𝐷 = 𝑆𝐴𝐸𝐹𝐺 теңдігін пайдаланып, басқадай теңдеуді аламыз:

(
𝑥 [720] + 1) = 720. 𝑥+10

DAE және FHC үшбұрыштарының ұқсастығын қарастыратын болсақ, онда келесі теңдік шығады: [𝑥(𝑥+10)] = 10.
720 1
Оқушыларға теңдеуді құрастырудың барлық тәсілдерін көрсеткен пайдалы және бастапқы мен соңғы теңдеулерге назар аударған дұрыс, өйткені олар квадрат теңдеуге жылдам көшеді. Барлық жағдайда да 𝑥[2] + 10𝑥 − 7200 = 0 теңдеуін шешеміз.
Көбінесе оқушылар үшін қозғалысқа арналған мәтінді есептерді шешу кезінде қозғалыста кешігу немесе тоқтау болған жағдайларда қиындықтар туғызады.
2- мысал. A және B қалаларының арақашықтығы 260 км. Автобус A қаласынан B қаласына шыққан соң 2 сағаттан кейін 30 минутқа тоқтады. Сондықтан кесте бойынша B қаласына уақытылы жету үшін ол жылдамдығын 5 кмсағ-қа арттырды. Автобустың бастапқы жылдамдығын табыңдар.
Шешуі. Есептің шарты бойынша геометриялық моделін салғанда үш тіктөртбұрыштың аудандарын пайдаланамыз. Біріншісі автобустың 2 сағатта жүріп өткен жолын (𝑆𝐴𝐵𝐿𝐾 ), ал екіншісі - автобустың тоқтап тұрған уақытында жүретін жолын (𝑆𝐾𝐿𝐸𝑁), үшіншісі - автобустың жылдамдығын арттырғандағы жүрген жолын (𝑆𝑁𝐹𝑀𝐷) көрсетеді (2-сурет). Мұның барлығы есепті шешудің бірінші кезеңінде, яғни мәтінін талдау кезінде айқындалады. Кейін есептің шартын геометриялық тілге аудару іске асады. Тіктөртбұрыштарға белгілеулер енгізіліп, олардың аудандары x айнымалысы арқылы өрнектеледі. Екінші кезеңде 𝑆1 мен 𝑆2 аудандарының теңдігін орнату іске асады. Олар тең болады, өйткені автобустың
тоқтап тұрған уақытында жүретін жолын (𝑆1) ол жылдамдығын 5 кмсағ-қа арттырып 𝑆2 жол жүріп қуып жетеді.
𝑆 = 𝑆 теңдігін және 𝑆 = 1 𝑥, 𝑆 = 5 𝐹𝑀, 𝐹𝑀 = 260−2𝑥 екенін ескеріп

1 2 1 2 2
𝑥+5

мынадай теңдеуді аламыз: [𝑥] = 5 [260−2𝑥], мұндағы х (кмсағ) - автобустың кесте
2 𝑥+5
бойынша жылдамдығы. Осы теңдеуді шешіп, автобустың кесте бойынша бастапқы жылдамдығын табуға болады.
3- мысал. Арақашықтығы 80 км болатын А қаласынан В қаласына велосипедші тұрақты жылдамдықпен шықты. Екінші күні ол кері қарай В қаласынан А қаласына алдыңғыға қарағанда 2 кмсағ-қа артық жылдамдықпен жүрді. Жол бойында 2 сағат тоқтады. Нәтижесінде кері қайтқанда А қаласынан В

қаласына жүрген уақытты жұмсады. Велосипедшінің А қаласынан В қаласына жүрген жылдамдығын табыңдар.
Шешуі. Велосипедші кері қайтқанда жылдамдығын 2 кмсағ-қа арттыра отырып, тоқтаған 2 сағат уақытын қуып жетеді. Сондықтан 3-суреттегі геометриялық моделді пайдаланып, мынадай теңдікті жазуға болады:

𝑆1 + 𝑆2 = 𝑆3, осыдан 2𝑡1 + 2𝑡2 = 2𝑥,
мұндағы х (кмсағ) - велосипедшінің А қаласынан В қаласына жүрген жылдамдығы, ал (𝑡1 + 𝑡2) - велосипедшінің кері қайтқанда жүрген уақыты.
Велосипедшінің кері қайтқанда жүрген уақыты [80] - -ге тең.
𝑥+2
Қорыта келе, мынадай теңдеуді аламыз:

2 80
𝑥+2
= 2𝑥 𝑥[2] + 2𝑥 − 80 = 0.

Соңғы теңдеуді шешіп, түбірлерін табамыз: 𝑥1 = 8, 𝑥2 = −10. Сонымен, велосипедшінің А қаласынан В қаласына жүрген жылдамдығы 8 кмсағ-қа тең болады.
Мектеп математика курсында судың бойымен қозғалысқа арналған есептер жиі кездеседі. Оларды да алгебралық және геометриялық әдістермен шешуге болады.

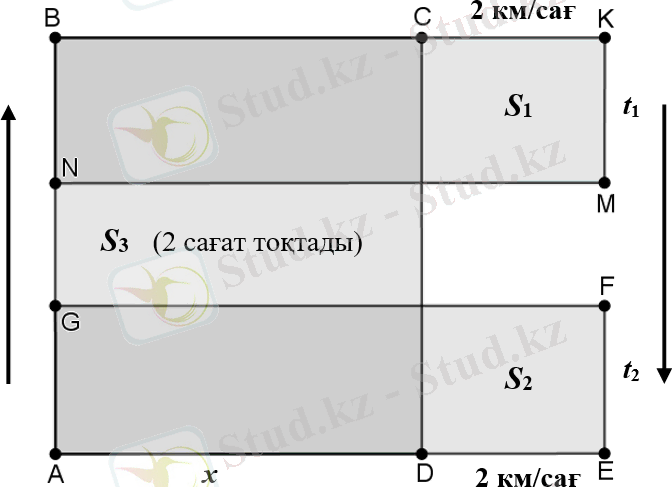
3-сурет

4- мысал. Моторлы қайық өзен ағысына қарсы 120 км жүзіп, бастапқы шыққан орнына кері қайтып келді. Кері қайтарда барған уақыттан 2 сағат аз жұмсады. Өзен ағысының жылдамдығы 1 кмсағ болса, қайықтың тұнық судағы жылдамдығын табыңдар.
Шешуі. Есептің геометриялық әдіспен шешейік, яғни шешу кезеңдерін қарастырамыз.

1- кезең. Геометриялық моделін құру. АВ = x (кмсағ) - қайықтың өзен ағысына қарсы жылдамдығы болсын (4-сурет). Сонда ABCD тіктөтбұрышының ауданы қайықтың өзен ағысына қарсы жүрген жолын анықтайды, яғни 120 км.

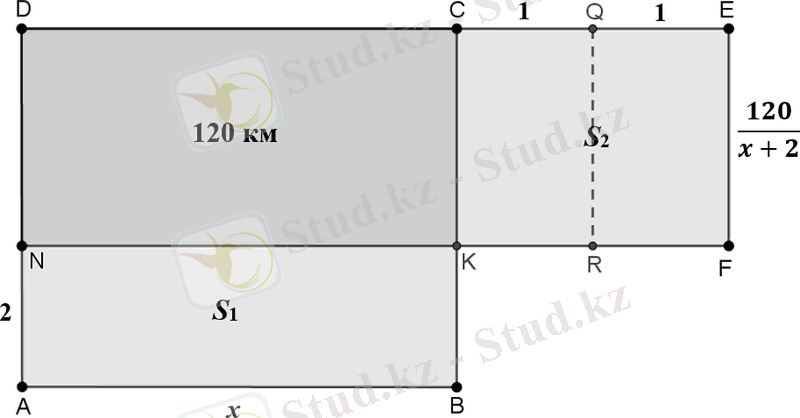
4-сурет

Кері қайтқанда (өзен ағысы бойымен) қайықтың жылдамдығы 2 кмсағ-қа артық болды. Сондықтан DC кесіндісіне CE = 2 кесіндісін қосамыз. DEFN тіктөртбұрышының ауданы қайықтың өзен ағысы бойымен жүзіп өткен жолын көрсетеді.
2- кезең. Есепті геометриялық тілде шешу. Қайық жылдамдығын арттыра отырып бастапқы орнына 2 сағат ерте келгендіктен, 𝑆1 = 𝑆2 болады, яғни

2𝑥 = 2 [120]
𝑥+2
𝑥 = 120
𝑥+2
𝑥[2] + 2𝑥 − 120 = 0.

Соңғы теңдеуді шеше отырып, оның түбірлерін табамыз: 𝑥1 = 10, 𝑥2 = −12.
Осыдан АВ = 10 екенін аламыз.
3- кезең. Табылған жауапты геометриялық тілден табиғи көшіру. Қайықтың өзен ағысына қарсы жылдамдығы 10 кмсағ, ал тұнық судағы жылдамдығы 11 кмсағ болады.
Алгебралық мәтінді есептерді шешу кезінде графикалық және графикалық- геометриялық әдістерді қолдануға болады. Графикалық әдіс функциялардың нақты графиктерін салуды талап етеді және бұл жағдайда есептің жауабы сызбаға қарап анықталады. Графикалық-геометриялық әдіс сызықтық функциялардың графиктерін схемалық түрде салуды және геометриялық қатынастар арқылы есептің аналитикалық шешімін алуды көздейді. Алдымен оқушыларды мәтінді есептерді графикалық әдіспен шешуді үйрету керек. Кейін геометрия курсында геометриялық фигураларды және олардың қасиеттерін (мысалы, ұқсас үшбұрыштардың қасиеттерін) өткеннен кейін графикалық-геометриялық әдісті үйреткен жөн.
Алгебра курсында оқушылар сызықтық функцияны және оның графигін салуды, екі айнымалысы бар сызықтық теңдеулер жүйесін графикалық тәсілмен шешуді меңгереді, ал физика курсында бірқалыпты процестердің графиктерімен

танысады. Сондықтан алгебра курсында мәтінді есептерді графикалық ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.