Молекулалық сутегі иондарының поляризациясы

Жұмыс түрі: Диссертация
Тегін: Антиплагиат
Көлемі: 31 бет
Таңдаулыға:

Кіріспе

1 БАЙЛАНЫСТЫ КҮЙЛЕРГЕ РЕЛЯТИВИСТІК ЕМЕС КВАНТТЫҚ ЕСЕПТІ ШЕШУ ҮШІН ВАРИАЦИЯЛЫҚ ӘДІС ЖӘНЕ ОНЫ ҚОЛДАНУ
1.1 Вариация әдісі
1.2 Минимакс принципі және Рицтің Вариациялық әдісі
1.3 Гелий атомының Вариациялық ыдырауының мысалдары
1.4 Толық орбиталық бұрыштық импульстің нөлдік емес мәні бар Хиллерастың
2 ЖҰҚА ЖӘНЕ ӨТЕ ЖҰҚА ДЕҢГЕЙ ҚҰРЫЛЫМЫ
2.1 Сутегі атомы
2.2 Гамильтондық өте жұқа өзара әрекеттесу
2.3 Қайтару әсерлерін ескере отырып, өте жұқа гамильтонианның пішіні.
3 МОЛЕКУЛАЛЫҚ СУТЕГІ ИОНДАРЫНЫҢ СТАТИКАЛЫҚ ЖӘНЕ ДИНАМИКАЛЫҚ ПОЛЯРИЗАЦИЯСЫ
3.1 Статикалық және динамикалық поляризация
3.2 Статикалық Старк эффектісі
3.3 Әлсіз айнымалы өріс. Скалярлық, тензорлық поляризация
3.4 Молекулалық сутегі иондарының поляризациясы
Қорытынды
ПАЙДАЛАНЫЛҒАН ДЕРЕККӨЗДЕРДІҢ ТІЗІМІ

Кіріспе

Көптеген күнделікті практикалық міндеттерді қамтитын физика, химия, биология және басқа ғылымдардың іргелі мәселелерін сәтті шешу үшін заттың сапалық және сандық құрамын, оның құрылымын, қасиеттерін және басқа параметрлерін температура мен қысымның кең шектерінде, әртүрлі агрегаттық күйлерде, шағын және үлкен концентрацияларда анықтауға мүмкіндік беретін Зерттеу әдістері болуы керек және басқа физикалық жағдайлар.
Барлық осы жағдайларды қанағаттандыратын әмбебап әдіс-спектроскопия. Спектроскопия-зерттеу объектісі сіңірген, шығарған, шашыраған немесе шағылысқан электромагниттік зерттеу арқылы заттың құрылымын зерттеумен айналысатын физика саласы. Толқын ұзындығына немесе энергияға ыдырайтын электромагниттік сәулелену спектрді құрайды .
Электромагниттік сәулелену спектрлері туралы барлық заманауи ілімдер кванттық теорияға негізделген, осылайша молекулалық спектроскопия кванттық заңдарға негізделген.
Кванттық көріністерді алғаш рет спектроскопияға Нильс Бор енгізді, ол 1913 жылы қарапайым атом - сутегі атомының спектрін түсіндірді. Бор тұжырымдаған екі постулат - стационарлық күйлердің болуы және сәулеленумен кванттық ауысулар туралы - болашақта атом физикасының орасан зор тәжірибелік материалында жан-жақты эксперименттік Растауды алды және кванттық механика мен кванттық электродинамикада терең теориялық негіздеме тапты. Бұл постулаттар қарапайымдыларға ғана емес, сонымен қатар ең күрделі атомдарға, молекулаларға және кристалдарға, бір жағынан атом ядроларына да қатысты болды. Атом жүйелері кез - келген микроскопиялық жүйелерді білдіреді-атом ядролары, атомдар, молекулалар, сондай-ақ жоғары өзара әрекеттесетін атомдар мен молекулалардан тұратын конденсацияланған макроскопиялық жүйелер.
Молекулалық спектрлердің сипаттамалық ерекшеліктері және олардың атомдық спектрлерден айырмашылығы екі атомнан тұратын диатомды және, әсіресе, кем дегенде үш атомнан тұратын көп атомды барлық молекулаларда қозғалыс неғұрлым күрделі түрде сипатталатындығымен анықталады. Электрондардың қозғалысымен қатар, салыстырмалы периодты тербелістер маңызды рөл атқарады ядролардың орналасуы - молекуланың тербелмелі қозғалысы және молекуланың кеңістіктегі бүтін бағдарындағы периодты өзгерістер - молекуланың айналмалы қозғалысы. Осылайша, молекулада қозғалыстың үш түрі бар - электронды, тербелмелі және айналмалы. Бұл молекулалық спектрлердің Атом спектрлеріне қарағанда едәуір күрделі болуына және әдетте өте тән көрініске ие болуына әкеледі. Көрінетін және ультракүлгін аймақтарда сызықтық спектрлердің орнына жеке немесе аз кең жолақтардан тұратын жолақты спектрлер алынады, олар жеткілікті дисперсиямен жеке жақын орналасқан сызықтарға рұқсат етілуі мүмкін - бұл молекулалардың электронды спектрлері. Жақын инфрақызыл аймақта молекулалар ерекше тербелмелі спектрлерге ие, олар жеке жолақтардан тұрады және жақын орналасқан сызықтарға үлкен дисперсиямен шешілуі мүмкін. Алыс инфрақызыл және микротолқынды аймақтарда жеке сызықтардан тұратын айналмалы спектрлер байқалады.
Сәйкес комбинациялық шашырау спектрлерін өлшеу арқылы байқалатын тербелмелі (тербелмелі-айналмалы) және айналмалы (таза айналмалы) ауысулар молекулалардың поляризациясымен байланысты бұрмалануларға ұшырайды. Молекуланың поляризациялануы оның электр өрісінің әсерінен индукцияланған (индукцияланған) дипольдік электр моментін алу қабілетімен анықталады және молекуланың маңызды сипаттамасы болып табылады. Шашырау жағдайында бұл индукцияланған момент түскен жарықтың әсерінен жасалады: классикалық тұрғыдан-түскен электромагниттік толқынның айнымалы электр өрісінің әсерінен.
Біз білетіндей, нөлден басқа дипольдік моменті бар молекулалар таза айналмалы сіңіру спектрлеріне ие. Мұндай молекулалар үшін сыртқы электр өрісіндегі молекуланың айналу деңгейлерінің бөлінуі маңызды рөл атқарады, яғни айналу деңгейлеріндегі Старк құбылысы .
Бұл диссертация кванттық механикадағы ең танымал интеграцияланбаған есептердің бірі болып табылатын кулондық өзара әрекеттесуі бар үш дененің кванттық есебін нақты қарастырады. Сонымен қатар, үш бөлшек жүйесі үшін байланысты күйлер мәселесі заманауи есептеу машиналарында қалағаныңызша дәл сандық шешімдерге мүмкіндік береді.
Соңғы жылдары ро-діріл спектроскопиясы арқылы Электрон массаларының Протонға, дейтр мен тритийге қатынасын дәлірек анықтау мақсатында молекулалық сутегі иондарын дәл зерттеу жүзеге асырылды .
Бұл жұмыста біз молекулалық сутегі иондарының дәл спектроскопиясына қатысты келесі мәселені қарастырамыз, атап айтқанда, сутектің негізгі изотопы Протонға қарағанда дәлдігі төмен белгілі тритонның, дейтр қасиеттерін зерттеу.
Молекулалық ион өткен ғасырдың 70-жылдарынан бастап сандық түрде зерттелді [7,8]. Салыстырмалы түрде жақында нералятивистік жуықтаудағы толық орбиталық моменті бар барлық діріл күйлерінің сандық есебі алынды. Диссертацияның негізгі мақсаты - бұл есептеулерді дәлдікпен көп күйлерге тарату жақсы қарағанда [9]. Есептеулерде көрсеткіштерде ерікті түрде таңдалған коэффициенттері бар Слатердің толқындық функцияларына негізделген өте дәл Вариациялық жуықтау қолданылады [10].
Вариациялық байланысқан күйдің толқындық функциялары үш бөлшекті Шредингер теңдеуінің кулондық өзара әрекеттесу шешімі негізінде Вариациялық жуықтауды қолдану арқылы есептелді экспоненттердің ыдырауы ерікті түрде таңдалған.
Диссертацияның міндеттерінің бірі-үш бөлшектің кванттық жүйесіндегі релятивистік емес энергия деңгейлерін, релятивистік және радиациялық түзетулерді есептеу. Байланысты күйлердің кванттық электродинамикасы екі бөлшек жүйесі үшін жақсы жасалғаны белгілі . Сонымен қатар, аналитикалық шешімнің болуы жоғары тәртіпте пайда болатын дивергенцияны азайту мәселесін шешуді едәуір жеңілдетеді. Алайда, бете-Солпитер теңдеуі немесе тиімді Дирак теңдеуі сияқты белгілі тәсілдердің көпшілігі бөлшектері көп жүйелерге жақсы таралмайды. Диссертация тиімді өріс теориясына, релятивистік емес кванттық электродинамикаға негізделген тәсілді қарастырады, бұл теорияны үш немесе одан да көп бөлшектерге жалпылауға мүмкіндік береді.
Жұмыстың жалпы сипаттамасы.
Жұмыс барысында сутектің молекулалық иондарының спектрлерін, , , және , соның ішінде өте жұқа құрылым мен әсерді, сыртқы өрістерді зерттеуге арналған.
Тақырыптың өзектілігі.
Жұмыс нәтижелері метрологияда үлкен маңызға ие. Біріншіден, іргелі физикалық тұрақтыларды нақтылау үшін, ең алдымен электронның Протонға қатынасының мәнін жақсарту үшін,. Статикалық және динамикалық поляризация мәндерінің өте дәл есептеулері зертханалық жағдайда уақыт бойынша негізгі тұрақтылардың вариациясын тексеру эксперименттері үшін үлкен маңызға ие болады. Жақында сутектің молекулалық иондарын қолдану және бөлме температурасында салыстырмалы тұрақтылығы шамамен 10-18 болатын өте дәл сағаттарды жүзеге асыру ұсынылды. Салыстыру үшін , 2011 жылы АҚШ ұлттық стандарттар және технологиялар институтында жүзеге асырылған цезий сағатында (қазіргі уақыт стандарты) қол жеткізілген ең жақсы дәлдік: 2.3*10-16.
Зерттеу нысаны.
Сутегі изотоптарының молекулалық иондары; олардың спектрі, оның ішінде деңгейлердің жұқа және өте жұқа құрылымы; сыртқы электромагниттік өрістердің әсерінен спектрдің өзгеруі.
Зерттеу әдістері: стационарлық Шредингер теңдеуін шешудің Вариациялық әдістері; релятивистік түзетулерді, өте жұқа құрылымның сдысуын, сыртқы өрістердің әсерінен деңгейдің сдысуын есептеуге арналған толқулар теориясы.

1 БАЙЛАНЫСТЫ КҮЙЛЕРГЕ РЕЛЯТИВИСТІК ЕМЕС КВАНТТЫҚ ЕСЕПТІ ШЕШУ ҮШІН ВАРИАЦИЯЛЫҚ ӘДІС ЖӘНЕ ОНЫ ҚОЛДАНУ
1.1 Вариация әдісі
1.2 Минимакс принципі және Рицтің Вариациялық әдісі
Біз байланысты күйлер үшін вариациялық принципті тұжырымдаймыз, сонымен қатар шешімнің негізгі ыдырау функцияларының түрін анықтайтын Вариациялық әдісті, сондай-ақ толқындық функцияларды құру кезінде Вариациялық параметрлерді таңдау стратегиясын ұсынамыз. Болашақта бұл әдісті "экспоненциалды" ыдырау деп атаймыз. Сондай-ақ, үш бөлшек жүйелеріне, соның ішінде молекулалық сутегі ионының негізгі күйіне және нөлдік емес орбиталық бұрыштық импульсі бар күйлерге арналған шешімдердің Вариациялық ыдырауын құрудың негізгі тәсілдеріне талдау жасайық.
Стационарлық Шредингер теңдеуінің Вариациялық әдістерімен шешудің бастапқы нүктесі,

(1.1)

кейбіреулер үшін гамильтониан H болып табылады. Хиллераас-Ундгеймнің Вариациялық принципі, математикада реле-Рицтің Вариациялық принципі ретінде жақсы белгілі, ол шамамен шешім қабылдауда әмбебап әдіс болып саналады. Вариациялық есептеудің негізгі міндеттері экстремумдарды немесе функционалдылықтың стационарлық мәндерін анықтауға арналған міндеттер болып табылады. Бұл әдістің мәні функционалдылықтың стационарлық мәндерін іздеу міндетін бірнеше айнымалылардың стационарлық мәндерін табудың түбегейлі қарапайым міндетімен ауыстыру болып табылады [13].
Гильберт кеңістігінде анықталған өзін-өзі байланыстыратын оператор H болсын , ол үшін Төменнен шектеу шарты орындалады

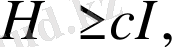(1.2)

Әрі қарай біз функционалдылықты анықтаймыз

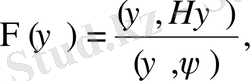(1.3)

бұл функционалдылық төменгі жағынан тұрақты мәнмен шектеледі .
Теорема 1. Шартты қанағаттандыратын өзін-өзі байланыстыратын оператор болсын (1.2). Біз анықтаймыз

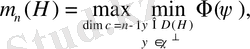(1.4)

мұндағы-ортогональды ішкі кеңістік-операторды анықтау аймағы . Содан кейін әрбір бекітілген немесе:
а) маңызды спектрдің шетінен төмен орналасқан меншікті мәндер бар (деградацияланған мәндерді олардың еселігі қанша рет есептегенде), яғни еселікті ескере отырып-меншікті мән;
немесе
б) - маңызды спектрдің төменгі шеті.
Меншікті мәндерді, яғни стационарлық Шредингер теңдеуінің байланысты күйлерінің энергиясын табу функционалдың седла нүктелерін есептеуге әкеледі (1.3). Теореманың тұжырымы "минимакс принципі"деп аталады.
Минимакс принципіне қатысты кейбір ескертулер жасауға болады:
1) минимакс принципі-операторлардың өзіндік мәндерін салыстыруға ыңғайлы құрал. Бұл спектрдің әртүрлі учаскелерінің орналасуын анықтайтын сандық және сапалық салдарларды анықтауға мүмкіндік береді (дискретті, үздіксіз спектрлер, еселіктер)
2) бұл әдіс қай жерде басталатынын анықтау үшін пайдалы болуы мүмкін - маңызды спектр.
3) кейбір жағдайларда белгілі бір жағдайларда және белгілі болған жағдайда , кем дегенде өзіндік мәні бар қорытынды жасауға болады. Осылайша, минимакс принципі кейбір жағдайларда дискретті спектрдің болуын анықтауға мүмкіндік береді.

Енді реле-Ритцтің Вариациялық принципін қолдана отырып, есептерді өз мәндеріне практикалық түрде шешу үшін және "Ритц процесі"деп аталатын әдісті қарастырайық
Екі талапқа бағынатын Гильберт кеңістігіндегі векторлар тізбегі болсын:
1) векторлар операторды анықтау аймағына жатады ;
2) кез келген жағдайда векторлар сызықтық тәуелсіз болады.
Скалярлық коэффициенттер қайда делік. Функционалдылыққа бекітілген кезде алмастыра отырып, біз параметрлердің соңғы жиынтығына байланысты функцияны аламыз

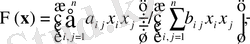
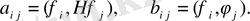
Осылайша минимакс шешімдерін іздеу жалпыланған есептің тиісті меншікті мәндерін меншікті мәндерге есептеуге дейін азаяды:

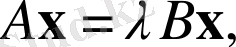(1.5)

матрицалар және коэффициенттерден тұрады және сәйкесінше.
Векторлар сызықтық емес параметрлерге байланысты болуы мүмкін . Бұл жағдайда меншікті мәннің әрбір тіркелген және нақты нөмірі үшін мәселе шешіледі (1.5) және таңдалады, содан кейін бұл мән сызықтық емес параметрлердің барлық мәндері бойынша азайтылады:

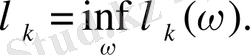
Рицті бағалау үшін бір маңызды қасиет орындалды:

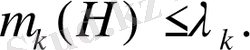(1.6)

Осы жерден Рицтің бағалары жоғарыдан бағаланады деген қорытынды жасауға болады. Сызықтық емес параметрлерге тәуелді негізгі функциялар үшін теңсіздік (1.6) мыналардан тұрады

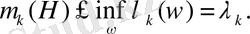
1-Теореманың түрдің гамильтонианымен релятивистік емес кванттық механика есептеріне қолданылуының қатаң дәлелі:

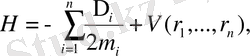(1.7)

Като еңбектерінен алынды .

1.3 Гелий атомының Вариациялық ыдырауының мысалдары
Енді гелий атомының негізгі күйін есептеу үшін қолданылатын Рицтің Вариациялық әдісін қолдану мысалдарын қарастырайық.
Екі электроны және шексіз ауыр ядросы бар Атом үшін релятивистік емес Шредингер теңдеуін жазайық

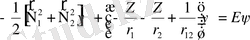(1.8)

мұндағы және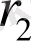-электрондардан ядроға дейінгі қашықтық, 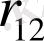-электрондар арасындағы қашықтық.
Алғашқы еңбектерінде Хиллераас Вариациялық функцияның негіз бойынша ыдырауын қолданды

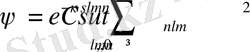(1.9)

жаңа айнымалылар енгізілген болатын: 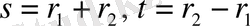және 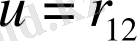. Скалярлық параметр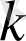, сондай-ақ коэффициенттер 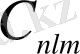.Вариациялық функционалдылықты азайту арқылы анықталды .
Ыдыраудың алғашқы 7 мүшесін қамтитын толқындық функциясы бар иондану энергиясының алынған мәні - 2.90324.
Кейінірек Киношита айнымалылар бойынша теріс дәрежелерді қосу үшін Хиллерастың негізін 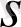және өзгертті ,

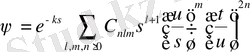
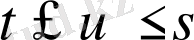теңсіздігінің арқасында, толқындық функция интеграция саласында ерекшеліктерге ие емес. Теріс дәрежелерді қолдану Вариациялық ыдыраудың конвергенция жылдамдығын арттыруға және 7 маңызды ( 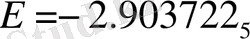) цифрда жоғары дәлдікке қол жеткізуге мүмкіндік берді. Барлық есептеулер UNIVAC компьютерінде жүргізілді.
Келесі қадам периметриялық координаттарды қолдануды ұсынған Пекеристің жұмысы болды:

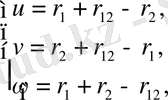
және ортогональды көпмүшелер (Лагерра көпмүшелері) толқындық функцияның ыдырауында:

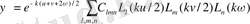(1.10)

Рекордтық дәлдікке жету үшін Пекериске 1078 негізгі функция қажет болды, ал энергияның мәні:
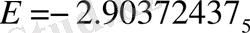
Периметрлік координаттардың артықшылығы - олар үшбұрыштың теңсіздігімен байланысты емес және іс жүзінде нөлден шексіздікке дейін өзгеретін тәуелсіз айнымалылар. Ортогональды көпмүшелерді қолдану сирек матрицаларға және бүтін арифметикадағы қайталанатын қатынастармен өрнектелетін матрицалық элементтерге әкеледі. Соңғы қасиет матрицалық элементтерді дәлдікті компьютер жадындағы өзгермелі нүкте сандарының көрінісімен байланыстырмай дәл есептеуге мүмкіндік береді. Әдістің осы артықшылықтары үшін төлем негізгі функциялардың санына байланысты Вариациялық ыдыраудың баяу конвергенциясы болып табылады.
Сонымен бірге Шредингер теңдеуінің негізгі күйге нақты шешімі түрдің таза көпмүшелік ыдырауы арқылы көрсетілмейтіні байқалды . Кейінірек Бартлетт және қатаң түрде Фок дәл шешімде бөлшектердің үштік соқтығысу нүктесінде аналитикалық ыдыраудағы логарифмдер бар екенін көрсетті. Дәлірек айтсақ 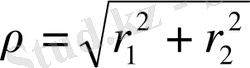, екі бөлшектің жүйесінің гиперрадиусы болса да, Шредингер теңдеуінің кішігірім шешімі 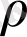түрінде ұсынылады:

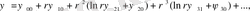(1.11)

Мұндағы 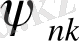функциялар тек бұрыштық айнымалыларға тәуелді және гиперсферадағы ақырлы және бір мәнді функциялар болып табылады ( ).
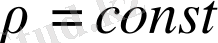Осы нәтижелерге сүйене отырып, алдымен Г. М.Шварц конвергенцияның үдеуін көрсете отырып, Хиллерастың ыдырауына жартылай бүтін дәрежелерді енгізеді, содан кейін Франковский мен Пекерис ыдырауға қосымша мүшелерді қосады :

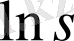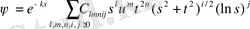(1.12)

Франковский мен Пекерис алған соңғы нәтиже ұзақ уақыт бойы үш ішінара жүйенің негізгі күйін иондаудың релятивистік емес энергиясы үшін ең дәл есептеу болды

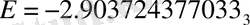
Салыстырмалы түрде жақында ч. Шварц жұмыста жоғарыда сипатталған ыдыраудың конвергенция жылдамдығын егжей-тегжейлі зерттеді. Ол сонымен қатар екі жаңа негізді енгізді:

(1.13)
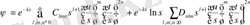(1.14)

Оның талдауы көрсеткендей, конвергенцияның ең жоғары жылдамдығы соңғы негізге ие, оның ішінде логарифм де, айнымалының теріс дәрежелері де бар . Релятивистік емес иондану энергиясының соңғы нәтижесі рекордтық дәлдікке ие және тең.

2. ЖҰҚА ЖӘНЕ ӨТЕ ЖҰҚА ДЕҢГЕЙ ҚҰРЫЛЫМЫ.

2.1 Сутегі атомы
Кулондық электростатикалық өзара әрекеттесу күштері атомдар ішінде әрекет ететін негізгі күштер болып табылады. Сутегі атомы үшін гамильтонды жазайық:

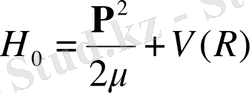(2.1)

Бірінші мүше - масса центрі жүйесіндегі атомның кинетикалық энергиясы, мұнда берілген масса, ал екінші мүше:

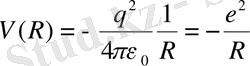(2.2)

электрон мен Протон арасындағы электростатикалық өзара әрекеттесу энергиясы, мұндағы электронның заряды .
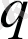Алайда, іс жүзінде өрнек жуықтау болып табылады, өйткені ол релятивистік әсерлерді ескермейді. Атап айтқанда, Электрон спинінің болуымен байланысты магниттік өзара әрекеттесу толығымен еленбейді. Сонымен қатар, протон-бұл өзара әрекеттесуге қосымша үлес қосатын 12 спині бар бөлшек. Бұл жағдайда жіберілген қате өте аз, өйткені сутегі атомы әлсіз релятивистік жүйе болып табылады. Есіңізде болсын , бор моделінде бірінші орбитадағы жылдамдық теңдікті қанағаттандырады 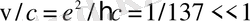, ал Протонның магниттік моменті де өте аз.
Дегенмен, Атом физикасындағы эксперименттердің жоғары дәлдігі гамильтониан негізінде түсіндіруге болмайтын әсерлерді оңай анықтауға мүмкіндік береді. Сондықтан жоғарыда аталған түзетулер ескеріліп сутегі атомының толық гамильтонын келесідей жазамыз:

(2.3)

мұнда оператор 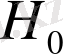(2.1) формуласымен анықталады және 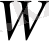оператор осы уақытқа дейін еленбеген барлық мүшелерді біріктіреді. Салыстырмалы түрде 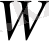операторы 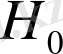аз болғандықтан, күтілетін әсерлерді жоғарыда келтірілген бұзылу теориясы арқылы есептеуге болады. Бұл бөлімде өзара әрекеттесудің болуы энергия деңгейлерінің "жұқа" және "өте жұқа құрылымына" әкелетіні көрсетілген. Спектрлік сызықтардың бұл бөлінуін өте жоғары дәлдікпен өлшеуге болады (сутегі атомының негізгі күйінің өте жұқа құрылымы физикалық шама болып табылады, ол қазіргі уақытта 14 маңызды цифрдың дәлдігімен белгілі).
Сондай-ақ, сыртқы статикалық өрістердің (электрлік және магниттік) сутегі атомының деңгейіне әсерін қарастырыңыз (Старк эффектісі).
Әрі қарай, әлсіз релятивистік аймақтағы Дирак теңдеуінен шығатын жұқа құрылымды гамильтонды қарастырайық. Басқаша айтқанда, біз түзетулерді шығарамыз, содан кейін олар гамильтонға (2.3) теңдеуден және Дирак теңдеуінен Протонның потенциал өрісінде қозғалатын электронға енеді , ол шексіз ауыр болып саналады және координаттардың басында Қозғалмай бекітіледі, содан кейін жүйе әлсіз релятивистік болған жағдайда осы теңдеудің шекті формасын іздейді. Бұл жағдайда электронның күйлері екі компонентті спинормен жақсы дәлдікпен сипатталады, ал паулиевтің жуықтауында теңдеуде электронның спин операторлары пайда болады, олар электронның орбиталық қозғалысымен әрекеттеседі, спин-орбиталық әрекеттесу. Ақыр соңында, гамильтониан үшін түрдің өрнегі алынады (2.3), мұнда оператор аналитикалық есептеуге болатын дәреже бойынша ыдырау түріне ие.
Осы презентация шеңберінде біз ыдыраудың алғашқы мүшелерін дәрежелер бойынша жазумен және оларды физикалық түсіндірумен шектелеміз:

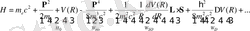(2.4)

Теңдікте (2.4) бірінші термин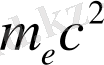- электронның тыныштық энергиясы, екінші және үшінші термин - релятивистік емес гамильтониан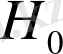, қалған терминдер Брейт-Паули гамильтонианының мүшелері деп аталады: электронның кинетикалық энергиясына релятивистік түзету 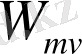, жұқа құрылымды түзету (немесе спин-орбиталық өзара әрекеттесу) 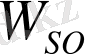, және Дарвин мүшесі (zitterbewegung), байланысты әлсіз релятивистік жуықтауға көшу кезінде электронның эрозиясы.
Әрі қарай, тікелей гамильтониан мүшелерінің физикалық табиғатын түсіндіруге көшейік.
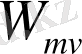бастайтын болсақ, тыныштық массасы 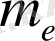мен импульсі бар классикалық бөлшектің энергиясы үшін релятивистік өрнек негізінде :

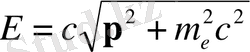(2.5)

және дәреже бойынша қатарға ыдырауды орындаймыз :

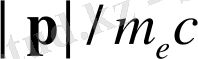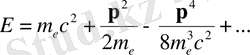(2.6)

мұндағы 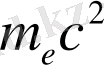тыныштық энергиясы, 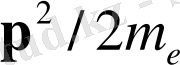кинетикалық релятивистік емес энергиясы, ал 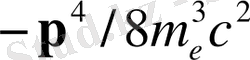мүлдем басқаша, болып табылады және массаның жылдамдыққа релятивистік тәуелділігімен байланысты энергияға түзетуден басқа ештеңе жоқ.
Бұл түзетудің шамасының ретін анықтау үшін 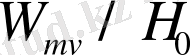қатынасты есептеу керек :

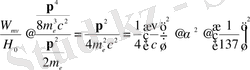(2.7)

өйткені сутегі атомы үшін 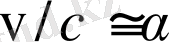. Өйткені 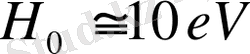болғандықтан, біз 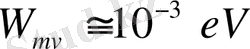аламыз .
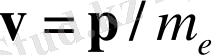Енді спин-орбиталық өзара әрекеттесуге жауапты мүшені қарастырыңыз . Электрон Протон жасаған электр өрісінде жылдамдықпен қозғалады. Арнайы салыстырмалылық электронды есептің өзіндік жүйесінде өрнекпен анықталған магнит өрісі 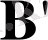пайда болатындығын көрсетеді:

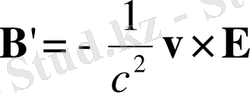(2.8)

Электронның өзіндік магниттік моменті болғандықтан 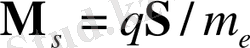, ол магнит өрісімен әрекеттеседі және бұл өзара әрекеттесу энергиясы тең болады:

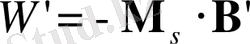. (2.9)

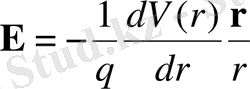формуласында, 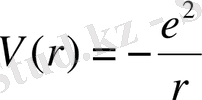- электронның электростатикалық энергиясы қайда екенін ескере отырып. Демек, бұл

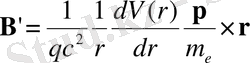. (2.10)

Тиісті кванттық операторда векторлық өнім пайда болады:

(2.11)

және қорытындылай келе:

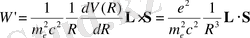. (2.12)

Бұл өрнек электронның магниттік спин моментінің магнит өрісімен әрекеттесуін физикалық түрде сипаттайды, ол Протонның электростатикалық өрісінде қозғалған кезде электронды "сезінеді".
Тәртіп болғандықтан мен ,үшін біз бар:

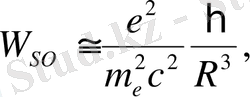(2.13)

ал қатынасты 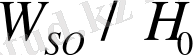формула бойынша бағалауға болады:

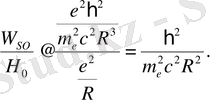(2.14)

Шаманың реті 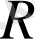бойынша бор радиусына 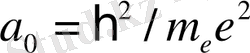сәйкес келетіндіктен, біз келесі формуланы аламыз:

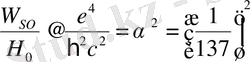. (2.15)

Әрі қарай, дарвиндік мүшені 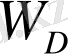, нақтырақ айтқанда оның физикалық табиғатын қарастырайық. Дирак теңдеуінде электрон мен ядроның Кулон өрісі арасындағы өзара әрекеттесу "Жергілікті" болып табылады; өріс энергияның өрнегіне оның мәні электрон орналасқан жерде енеді. Алайда, электронның күйін сипаттайтын екі компонентті спинор үшін релятивистік емес жуықтау (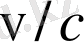дәреже бойынша ыдырау ) электрон мен өрістің өзара әрекеттесуі "жергілікті емес" болатын теңдеуге әкеледі: электрон кеңістіктік ұзындығы 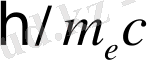электронның комптондық толқын ұзындығының реті бар нүктеде центрі бар аймақтағы өріс мәндерінің тұтас ансамблін "сезінеді". Бұл Дарвин терминімен ұсынылған түзетудің табиғаты.
Оған дәлірек физикалық мағына беру үшін электронның потенциалдық энергиясы 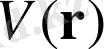интегралдық өрнекке тең емес делік:

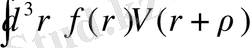(2.16)

мұндағы 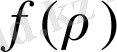функция, оның интегралы 1-ге тең және ол тек нүктеде центрі бар тәртіп көлемінде маңызды мәндерді қабылдай отырып 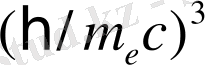, тәуелді болады .
Егер біз тәртіп арақашықтықтарындағы тәуелділікті елемейтін болсақ, онда (2.16) формуласында оны 1-ге тең болатын интегралдың астынан ауыстыруға және шығаруға болады, ал (2.16) өрнегі азаяды .
Осылайша, жақсырақ жуықтау үшін (2.16) потенциалды оның Тейлор қатарына жақын ыдырауына ауыстыру керек . Нөлдік ретті мүше береді; бірінші ретті мүше функцияның сфералық симметриясына байланысты нөлге айналады; екінші ретті мүше нүктеде потенциалдық энергияның екінші туындыларын және С-мен өлшенген және интеграцияланған компоненттердің квадраттық функцияларын қамтиды , бұл тәртіптің нәтижесіне 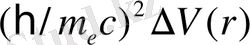әкеледі . Осылайша, дәл осы екінші ретті мүше Дарвин терминін құрайтыны көрінеді.
Шаманың реті туралы айта отырып, мәнін ауыстыра отырып , Дарвин өрнегін келесі түрде қайта жазуға болады:

(2.17)

Егер атомдық күйдегі (2.17) орташа мәнді есептесек, онда біз тең үлес аламыз:

Мұндағы -санаудың басындағы толқындық функцияның мәні. Осылайша, Дарвин өрнегі тек S электрондарына әсер етеді, өйткені олар үшін жалғыз . Шаманың ретін толқындық функция Модулінің квадратының интегралын Бор радиусы 1 болатын тәртіп көлемі бойынша жазу арқылы алуға болады. Соңында біз келесі формуланы өрнектеп аламыз :

(2.18)

Дарвин өрнегінің шамасының ретін бірден не береді:

. (2.19)

болғандықтан бұл жолы да біз:

(2.20)

Жұқа құрылымның барлық мүшелері релятивистік емес гамильтоннан шамамен бір есе кіші.

2.2 Гамильтондық өте жұқа өзара әрекеттесу
Теңдеудегі оператордың алғашқы екі термині нөлдік үлес береді.
Шынында да, бірінші терминнің үлесін есептеу нөлге тең" бұрыштық " матрицалық элементтерді табуға дейін азаяды .
Сол сияқты, екінші терминнің матрицалық элементтері (диполь-диполь әрекеттесуі) күйдің сфералық симметриясына байланысты нөлге тең екенін көрсетуге болады .
Өрнектің соңғы терминінің матрицалық элементтері, яғни байланыс термині келесідей:

(2.21)

Егер сіз көрініске өтсеңіз, осы матрицалық элементтің орбиталық және спиндік бөліктерін бөліп, оны формада ұсынуға болады:

(2.22)

мұндағы- сан, ол келесі мәнге тең:

(2.23)

Мультипликатор берілген масса кіретіндіктен пайда болады . Байланыс термині үшін ядроны қатайту әсерінің дұрыс есебі дәл осылай жүзеге асырылады, сонымен қатар алдыңғы формулада көрсетілген және байланыстыратын өрнектер, сондай-ақ жұмыста алынған радиалды функцияға арналған өрнек қолданылады .
Осылайша, орбиталық айнымалылар толығымен жоғалады және тапсырма екі спин және түрдің өзара әрекеттесуімен байланысты бұрыннан белгілі мәселеге дейін азаяды:

(2.24)

Мұндағы тұрақты шама.
Әрі қарай, байланыс терминінің меншікті күйлері мен меншікті мәндерін қарастырыңыз. Елестету үшін, оператор, осы уақытқа дейін біз тек негізді қолдандық:

(2.25)

операторларға ортақ меншікті векторлар құралған . Негізгі күй үшін толық бұрыштық импульсті де енгізуге болады:

(2.26)

және негізін қолдану арқылы:

(2.27)

операторларға ортақ меншікті векторлардан құралған . Өйткені кванттық сан тек екі мәнді қабылдай алады және .
Негіз операторды зерттеу үшін негізге қарағанда жақсы , өйткені бұл оператор негізде диагональды матрицамен ұсынылған (қарапайымдылық үшін біз нақтылауды және ). Шынында да, формула мынаны білдіреді

(2.28)

және бұл күйлер оператордың меншікті күйлері болып табылады :

(2.29)

Бұл өрнектен меншікті мәндер тәуелді, бірақ тәуелді емес тең екенін көруге болады:

(2.30)

Жәнеүшін;

(2.31)

Және үшін.
Осылайша, деңгейдің төрт еселенген деградациясы ішінара бұзылу арқылы жойылады: үш рет деградацияланған деңгей және деградацияланбаған деңгей пайда болады . Деңгей еселігінің деградациясы айтарлықтай және оператордың толық жүйенің айналуына қатысты инварианттылығымен байланысты.
Енді өте жұқа деңгей құрылымын қарастырыңыз . Әсер ету кезінде деңгейдің энергиясы мәнге қатысты шамаға төмендейді . Оператор деңгейді екі өте жұқа ішкі деңгейге бөледі, олардың арасындағы энергия аралығы (2.2-сурет). Шаманы Көбінесе "Негізгі күйдің тұрақты ультра жұқа құрылымы"деп атайды.

2.2-сурет Сутегі атомы деңгейінің өте жұқа құрылымы.

Оператордың әсерінен деңгей жалпы ауысуды бастан кешіреді; кванттық сан тек бір мәнді қабылдай алады . Өте жұқа өзара әрекеттесуді есепке алу деңгейдің екі өте жұқа ішкі деңгейге бөлінуіне әкеледі және . Өте жұқа ауысу (радиоастрономияда кеңінен қолданылатын толқын ұзындығы 21 см) 12 маңызды цифрмен белгілі жиілікке ие, бұл сутегі масерін жасау арқылы эксперименталды түрде алынған)
Кейбір ескертулерді атап өтейік: оператор жұқа құрылым деңгейлерінің әрқайсысының бір-бірінен ерекшеленетін және I арасындағы барлық мүмкін мәндерге сәйкес келетін өте жұқа деңгейлер қатарына бөлінуіне әкеледі . Деңгейлер үшін кванттық сан, яғни екі мәнді алады: және . Бізде деңгей үшін, яғни мүмкін мәндер және (2.3-сурет).

2.3-сурет Сутегі атомы деңгейінің өте жұқа құрылымы

Екі деңгей арасындағы Интервал және деңгейлерді бөлетін жұқа құрылым интервалынан шамамен он есе аз ламбиялық сдысу және . Өте жұқа өзара әрекеттесуді есепке алу әр деңгейдің екі өте жұқа ішкі деңгейге бөлінуіне әкеледі (кванттық санның мәндері суреттің оң жағында көрсетілген). Ультра жұқа бөліну деңгей үшін 23,7 МГц , деңгей үшін 177,56 МГц және деңгей үшін 59,19 МГц (түсінікті болу үшін сызбаның масштабы сақталмайды)
Өте жұқа деңгей құрылымының маңыздылығы туралы айтатын болсақ, сутегі атомының негізгі деңгейінің өте жұқа құрылымы қазіргі уақытта эксперименталды түрде ең жоғары дәлдікпен алынған физикалық шама деп айтуға болады:

(2.32)

Мұндай эксперименттік дәлдік 1963 жылы "сутегі масерінің"құрылуының арқасында мүмкін болды. Бұл құрылғының жұмыс принципін схемалық түрде келесідей ұсынуға болады. Сутегі атомдары Стерн және Герлах типті магниттік ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.