Бастауыш сыныпта комбинаторлық есептерді шешудің негізгі әдістері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ

МАМАЖАНОВА АЛУА, МУКАНОВА ЖАННА, БЕКАРЫСОВА АЯЖАН

БАСТАУЫШ СЫНЫПТАРДАҒЫ КОМБИНАТОРЛЫҚ ЕСЕПТЕР ЖИНАҒЫН ҚҰРАСТЫРУ тақырыбына

ДИПЛОМДЫҚ ЖОБА

6В01301-Бастауышта оқыту педагогикасы мен әдістемесі
мамандығы бойынша

Алматы, 2023

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ

Бастауыш білім беру бағдарламалары
кәсіби даярлау бөлімінің жетекшісі
____________________ А.Е.Жұмабаева

ДИПЛОМДЫҚ ЖОБА

ТАҚЫРЫБЫ: БАСТАУЫШ СЫНЫПТАРДАҒЫ КОМБИНАТОРЛЫҚ ЕСЕПТЕР ЖИНАҒЫН ҚҰРАСТЫРУ

6В01301-Бастауышта оқыту педагогикасы мен әдістемесі м
амандығы бойынша

Орындағандар: күндізгі оқу бөлімінің 4-курс студенттері
Мамажанова А.,Муканова Ж.,Бекарысова А.

Ғылыми жетекшісі: PhD доктор, аға оқытушы Астамбаева Ж.Қ.

Алматы, 2023
БАСТАУЫШ СЫНЫПТАРДАҒЫ КОМБИНАТОРЛЫҚ ЕСЕПТЕР ЖИНАҒЫН ҚҰРАСТЫРУ

МАЗМҰНЫ

КІРІСПЕ
БАСТАУЫШ СЫНЫПТАРДАҒЫ КОМБИНАТОРЛЫҚ ЕСЕПТЕР ЖИНАҒЫН ҚҰРАСТЫРУ

§1
КОМБИНАТОРИКАНЫҢ НЕГІЗГІ ҰҒЫМДАРЫ туралы түсінік

§2
Комбинаторлық есептердің түрлері

§3
Бастауыш сыныпта оқыту үшін Комбинаторлық есептер жиынтығын құрастыру

ҚОРЫТЫНДЫ

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР

ҚОСЫМША

Кіріспе

Зерттеудің өзектілігі
ьььььььььь

Комбинаторлық есептер бастауыш сыныпқа арналған математика оқулықтарында Л.Г.Петерсон [1], Н.Б.Истомина [], М.И.Башмакова [], М.И.Моро және т.б авторлардың шығарған.Олар қиындығы жоғары есептер болып саналатынын және жиі кездеспейтінін айта кету керек, бірақ оларды шешу мүмкін. Сонымен қатар зерттеушілік, шығармашылық немесе ойын әрекеті форматында ұйымдастырылады, бұл кіші жастағы оқушылардың қызығушылығын тудыратыны сөзсіз.
Жұмыстың мақсаты: Бастауыш сыныптағы комбинаторлық есептерді шығаруға үйрету әдістерін зерттеу.
Жұмыстың міндеттері:
1. Бастауыш сыныптағы математика сабағында есептерді шығарудың негізгі әдістерін анықтау.
2. Бастауыш сыныпта оқыту үшін Комбинаторлық есептер жиынтығын құрастыру.

Зерттеу нәтижелерінің практикалық маңыздылығы: әзірленген Комбинаторлық есептер жиынтығы математика сабақтарында да, сыныптан тыс жұмыстарда да қолдануға болады.
Зерттеу құрылымы: Дипломдық жұмыс кіріспеден, екі тараудан қорытындыдан және пайдаланған әдебиеттер тізімінен тұрады.
Жоба командасының сипаттамасы төмендегідей тақырыпты зерттеп, сонымен қатар дипломдық жобаны бөлімдер бойынша бөліп көрсеткен 6В01301-Бастауышта оқыту педагогикасы мен әдістемесі мамандығының 4-курс студенттері: Муканова Жанна - кіріспе бөліміне жауапты.
Мамажанова Алуа - 1-2 тарауға жауапты.
Бекарысова Аяжан - қорытынды бөліміне жауапты.

Жобаны іске асыру кезеңдері:
1.Бірінші кезеңде (2022 қыркүйек-желтоқсан) дипломдық жоба тақырыбына шолу жасалып, деректер жинақталды. Алынған мәліметтер өңделіп, талданғаннан кейін жобаның негізгі бағыттары белгіленді. Дипломдық жобаның негізгі тұжырымдамалары берілді.
2.Екінші кезеңде (2022 ж. желтоқсан - 2023 ж. қаңтар) оқу жоспары мен әдістемелік жұмыстар, озық тәжірибелер негізінде дайындалды, тапсырманы орындау үшін ресурстар таңдалды. Жобаның қорытындылары жинақталып, ІІІ тоқсанның Табиғат құбылыстары бөліміне арналған дидактикалық материалдар жинағы тәжірибеге енгізілді.
3.Үшінші кезеңде (2023 жылдың ақпан-сәуір айлары) 4-сыныптың Дүниетану пәні бойынша дидактикалық материалдар жұмысы сәтті аяқталып, дипломдық жоба техникалық талаптарға сәйкес орындалды.

Жобаны дамыту перспективалары:

1 БАСТАУЫШ СЫНЫПТА КОМБИНАТОРИКАНЫҢ НЕГІЗГІ ҰҒЫМДАРЫ

§1 Қомбинаторика ұғымының түсінігі
Берілген жиындағы элементтерден қандай да бір шартқа бағынатын әртүрлі қанша комбинация құрастыруға болады деген сұрақты қарастыратын математика саласын комбинаторика деп атайды.
Комбинаторика ұғымы XVI - ғасырда пайда болған. Ол кезде карта, сүйек ойыны, лотереялар сияқты құмарлық ойындар үлкен орын алған. Сондықтаналғашқыда комбинаторикалық есептер негізінен құмарлық ойындарға қатысты болған. Комбинаториканың дамуы Я.Бернулли, Лейбниц, Эйлер есімдерімен тығыз байланысты.
Соңғы жылдары комбинаторика жедел даму үстінде. Комбинаторикалық әдістер транспорттық есептер шешуде, кестелер, өндірістік жоспарлар құрастыруда және өнімді өткізу мәселесінде қолданылады. Комбинаториканың негізгі ұғымдары көптеген ықтималдық есептерінің, сызықтық программалаудың, статистиканың негізі болып табылады. Сонымен қатар, комбинаторика автоматтар теориясында, экономикалық есептерде, биология және генетикада қолданылады.
Берілген жиын n әртүрлі элементтерден тұрсын. Бұл жиыннан бір элементті аламыз, содан кейін жиыннан бұл элементтен басқа екінші элемент алынады т.с.с., яғни әрбір таңдауда алынған элементтерден басқа жаңа элементтер алып отырамыз. Бұл кайталанбайтын таңдау.
Берілген жиын k типті элементтерден тұратын болсын, мұнда әрбір типтің ішіндегі элементтер бірдей. Кезекті таңдауда, алдыңғы алғаннан басқа, немесе алдында алғандағыдай жаңа элемент аламыз. Бұл қайталанатын таңдау деп аталады.
Қайталанатын таңдауға өзгеше сипат беруге болады. Берілген жиын әртүрлі п элементтен тұрсын. Бірінші элементті жазып алып, оны жиынға қайта қайтарамыз. Екінші элементті аламыз. Бұл жаңа немесе алдыңғы қайтарылған элемент болуы мүмкін. Мұндай таңдау қайталанатын таңдау. Жиыннан алынған элементтер таңдауларды құрайды.
Есеп шығаруда қолданылатын комбинаторикалық әдістің бірі - жалпы бір схемаға негізделген бұтақтар әдісі. Мүмкін таңдау саны әр қадам сайын алғашқыда қандай элемент алынғанына байланысты болатын комбинацияны құру процесін бұтақтар түрінде қарастырған ыңғайлы. Алдымен бір нүктеден әр түрлі неше таңдау алуға болатын бағыт көрсетіледі, яғни әрбір тармақ бір элементке сәйкес келеді. Алынған бағыттардан, екінші қадамда қанша таңдау жасауға болса, бір нүктеден сонша мүмкіндіктер тармақтары (стрелка) жүргізіледі.

2 Бастауыш сыныпта комбинаторлық есептерді шешудің негізгі әдістері
Комбинаторлық есептерді шешуді оқыту әдістемесі кіші мектеп оқушыларына математикалық білім беруді дамытудың әдістемелік жүйесі аясында Н.Б. Истомина әзірлеген. Бұл әдістеме математиканың бастапқы курсының мазмұнын меңгеру процесінде ақыл-ой әрекеті әдістерін мақсатты және жүйелі түрде қалыптастыру қажеттілігін білдіреді.
Комбинаторлық есептерді шешу талдау және синтез, салыстыру, жіктеу, жалпылау сияқты логикалық әдістерді белсенді қолдануды талап етеді.
Комбинаторлық есептерді шешу әдістері әдетте екі топқа бөлінеді: формальды және бейресми. Формальды шешім арқылы үлгінің сипатын анықтау керек, сәйкес формуланы немесе комбинаторлық ережені таңдап, сандарды ауыстырып, нәтижені есептеу керек. Нәтиже - мүмкін болатын нұсқалардың саны, бірақ бұл жағдайда опциялардың өзі қалыптаспайды. Бұл шешім жолын бастауыш сынып оқушылары пайдаланбайды.
Бастауыш сынып оқушылары үшін шешудің бейресми әдісі әртүрлі комбинаторлық конфигурацияларды құрастыру процесінің өзін әкеледі. Оның негізгі міндеті - барлық мүмкін нұсқаларды дұрыс табу.
Комбинаторлық есептерді шешудің бейресми әдістеріне тікелей санау жатады. Бұл ең қарапайым әдіс, өйткені. ол анықтамалар мен формулаларды білуді талап етпейді. Сондықтан оны бастауыш сыныптарда қолданған жөн.
Комбинаторлық есептерді бейресми әдіспен шешуді үйрену үш кезеңде жүзеге асырылады:
1. Дайындық кезеңі (1-сынып). Бұл кезеңнің мақсаты - ретсіз санау әдісімен комбинаторлық есептерді шешу барысында ой операцияларын қалыптастыру. Дайындық кезеңінде балаларға танымдық қабілеттерін дамытуға, талдау, синтез, салыстыру, жалпылау сияқты ойлау процестерін белсендіруге арналған тапсырмалар ұсынылады. Бұл балаларға оңай елестетуге болатын өмірлік тапсырмалар (адамның күнделікті өмірде шешетін тапсырмалары) болуы мүмкін.
Мысалы, логикалық қыздыру кезінде комбинаторлық есептерді шешуге мотивация беру үшін адамның күнделікті іс-әрекетінде комбинаториканы қолдану мүмкіндігін көрсететін өмірлік есептерді шешуге болады.
Міне, осындай тапсырманың мысалы: Төрт жігіт кинотеатрдың кассасында тұр. Олардың екеуінде жүз сомдық, қалған екеуінде елу сомдық купюралар бар. Кинотеатрға билет құны 50 теңге болса, ешкім ақшаны ауыстыруды күтпеуі үшін жігіттер қалай жайғасу керек?
Есеп практикалық әдіспен (ойнау) шешіледі. Тақтаға бес оқушы келеді: 4 сатып алушы (мұғалім оларға 50 және 100 теңгелік шоттарды береді) және кассир (билеттерді алады). Сату басында кассаның бос екендігі келісілді. Нәтижесінде балалар екі ықтимал шешімді табады:
1) 50 теңге, 100 теңге, 50 теңге, 100 теңге;
2) 50 теңге, 50 теңге, 100 теңге, 100 теңге.
Осылайша, дайындық кезеңінде комбинаторлық есептерді шешуге оң мотивация туғызу, оқушыларды одан әрі күрделі есеп түрлерін шешуге дайындау, сонымен қатар психикалық операцияларды: талдау, синтез, салыстыру, жалпылауды жетілдіруге жағдай жасау қажет.
2. Негізгі кезең (2-3 сыныптар).
Бұл кезеңнің мақсаты студенттерді әртүрлі модельдер: кесте, график және ықтимал нұсқалар ағашы арқылы ұйымдастырылған санау әдісімен таныстыру болып табылады [1]. Мектеп оқушыларын ұйымдық санау әдісімен таныстырғанда, барлық шешімдерді қарастырудың белгілі бір реттілігін сақтай отырып, балаларды санауға үйрету маңызды.
Ықтималдықтар теориясы тек кездейсоқ оқиғалар және олардың пайда болу мүмкіндіктерін қарастыратын математиканың бір бөлімі болып табылады. Сонымен қатар, ықтималдықтар теориясы қандай да бір оқиғаның шығуын алдын-ала анықтай алмайды, бірақ оның көмегімен көп рет қайталанған оқиғаның заңдылығын анықтауға болады. Оқиғалар 3 түрге бөлінеді: ақиқат, мүмкін емес және кездейсоқ.
Тәжірибе барысында міндетті түрде орындалатын оқиғаларды ақиқат оқиғалар деп атайды.
Тәжірибе кезінде пайда болмайтын оқиға мүмкін емес оқиға деп аталады.
Тәжірибе барысында орындалуы да, орындалмауы да мүмкін оқиға кездейсоқ деп аталады.
Оқиғалар латын алфавитінің бас әріптерімен А, В, С,... арқылы белгіленеді.
Тәжірибе барысында екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғалар үйлесімсіз деп аталады.
Тәжірибе кезінде мүмкін оқиғалардың әйтеуір біреуінің пайда болуы ақиқат болса, онда оқиғалар жалғыз мүмкіндікті оқиғалар деп аталады. Егер А, В, ...,М. оқиғалары жалғыз мүмкіндікті болса, онда олар толық топты құрайды. Егер жалғыз мүмкіндікті екі оқиға толық топты құраса, онда олар қарама-қарсы оқиғалар деп аталады. А оқиғасына қарама-қарсы оқиғаны деп белгіленеді.
Тәжірибе мен оқиға ұғымдарының айырмашылығын қарастырайық. Өмірде, тұрмыста, ғылымда жүргізілетін бақылаулар, сынақтар, экспери-менттерді тәжірибе деп атаймыз. Тәжірибенің нәтижесі оқиға болады.
1-мысал. Теңге бір рет лақтырылады. Бұл тәжірибе. Тәжірибенің нәтижесі оқиға болып есептеледі.
А оқиғасы - елтаңба жағының шығуы.
В оқиғасы - цифр жағының шығуы. Мұнда А және В үйлесімсіз (тоғыспайтын), қарама-қарсы оқиғалар және толық топ құрайды.
2-мысал. Жәшікте тек ақ шарлар бар. жәшіктен ақ шар алу - бұл ақиқат оқиға, ал жәшіктен қара шар алу - бұл мүмкін емес оқиға.
3-мысал. Жәшікте ақ, қара және қызыл шар бар. Бір шар алынады. Бұл тәжірибе болса, ал тәжірибенің нәтижесі мынадай оқиғалар болуы мүмкін.
А - ақ шар алынды.
В - қара шар алынды.
С - қызыл шар алынды.
Бұл оқиғалар үйлесімсіз оқиғалар және толық топ құрайды. Бірақ бұл оқиғалар қарама-қарсы оқиғалар бола алмайды. Қарама-қарсы оқиғаларда тек екі оқиға толық топ құрастырады. Ал біз қарастырып отырған жағдайда үш оқиға бар.
Кездейсоқ оқиғаның орындалуы да мүмкін, орындалмауы да мүмкін. Оның орындалу мүмкіндігі әртүлі болады. Табысқа жету мүмкіншілігін оқиғаның орындалуы барысында оның жиілігі бойынша салыстырылады.
Анықтама. Мүмкіншіліктің (шанстың) мән-мағынасын бөлшек сан ретінде қарастыруға болады. Оның алымы - орындалған оқиғалар саны, ал бөлімі барлық жағдайлар санын көрсетеді.
1-мысал. Жәшікте 5 ақ шар және 10 қара шар бар. Бір шар алынады.
A - ақ шар алынды
B - қара шар алынды
C - қызыл шар алынды
D - ақ немесе қара шар алынды. Аталған оқиғалардың шығу мүмкіндіктерін тап.
Шешуі: Жәшікте барлығы 15 шар. Сонда оқиғаның болу мүмкіндіктері төмендегідей болады.
A - 15- тен 5 мүмкіндік, демек бөлшек түрінде
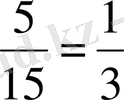
B - 15- тен 10 мүмкіндік, демек бөлшек түрінде
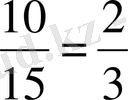
C - 15- тен 0 мүмкіндік, демек бөлшек түрінде
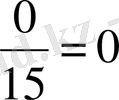
D - 15- тен 5+10=15 мүмкіндік, демек бөлшек түрінде
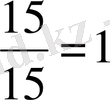
Мұнда А және В оқиғасы кездейсоқ. С - мүмкін емес оқиға, D - ақиқат оқиға. Көріп тұрғандай ақиқат оқиғаның мүмкіндігі 1- ге тең, мүмкін емес оқиғаның мүмкіндігі 0- ге тең, ал кездейсоқ оқиғалардың мүмкіншілігі 0 мен 1 аралығында орналасқан. Сонда ықтималдар шкаласында былай көрсетуге болады.

Мүмкін емес кездейсоқ ақиқат
0 1

2-мысал. 36 ойын картасының топтамасынан бір карта суырылып алынады. Оның келесі оқиғаларда орындалу мүмкіндігін анықтау немесе оны ықтималдар шкаласына орналастыру керек.
A - бұл карта тұз болады
B - бұл карта король болады
C - бұл карта қызыл түсті болады
D - бұл карта қарға болады
E - бұл карта алтылық болады
Шешуі. Оқиға үшін табысқа жету мүмкіншілігін анықтайық.
А - 36-дан 4 мүмкіндік, яғни
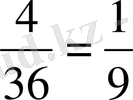
В - 36-дан 4 мүмкіндік, яғни

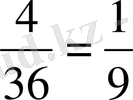
C - 36-дан 18 мүмкіндік, яғни
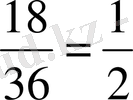
D - 36-дан 9 мүмкіндік, яғни
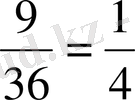
E - 36-дан 4 мүмкіндік, яғни
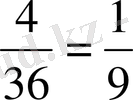
Онда ықтималдық көрсеткіште келесі реттілікпен олар солдан оңға қарай орналасқан: В, А және Е, D, С.

0 В АE D C 1

Мына мысалды қарастырайық. Жәшікте 6 стандартты және 4 стандартты емес зат бар. Жәшіктен бір зат алынған. Стандартты затты алу мүмкіндігі стандартты емес затты алуға қарағанда көп екені айқын. Бұл мүмкіндікті сипаттайтын сан ықтималдық деп аталады.
Анықтама. А оқиғасының ықтималдығы дегеніміз - осы оқиғаға қолайлы жағдайлар санының барлық жағдайлар санына қатынасы.
А оқиғасының ықтималдықтығы былай белгіленеді Р(А). Сонымен,
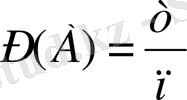(8)
Кез - келген А оқиғасының ықтималдығы келесі шарттарға тәуелді:
1.
2. 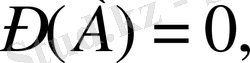егер А - мүмкін емес оқиға болса
3. 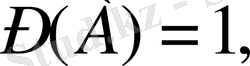егер А - ақиқат оқиға.
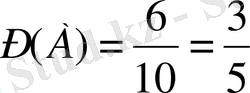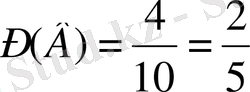Сонымен жоғарыда келтірілген мысалда бір детальді алу оқиғасының орындалуының мүмкін саны 10- ға тең, яғни N=10. А - Стандартты детальды алу - оқиғасының орындалу саны 6- ға тең, яғни m=6. Онда А - оқиғасының ықтималдығы тең. Дәл сол сияқты В - стандартты емес детальды алу- оқиғасының ықтималдығы тең.
3. Бастауыш сыныпта оқыту үшін Комбинаторлық есептер жиынтығын құрастыру

Бастауыш сыныпта бағдарламаларына арналған математика оқулықтарын талдау барысында комбинаторлық есептер оларда аз мөлшерде кездеседі, олардың түрлері әртүрлі емес деген қорытындыға келдік. Сондықтан біз өз жұмысымызда сабақта да, сабақтан тыс уақытта да қолдануға болатын Комбинаторлық есептер жиынтығын құруды шештік. Бұл жинаққа біз қарастырған оқулықтарда кездеспейтін немесе сирек кездесетін тапсырмаларды енгізуді ұйғардыңыз. Комбинаторлық есептер жиынтығын құрастыру кезінде біз Н.Б. Истоминаның Комбинаторлық есептерді шешуді үйрену ережесіне сүйендік [], өйткені автор оларға әртүрлі типтегі, күрделілік деңгейі әртүрлі, әртүрлі түрде шешілген көптеген есептерді енгізді.(соның ішінде біз оқулықтарда көрмеген үлгілерді пайдалану).
1. 0 және 1 цифрларынан қанша төрттаңбалы сан құрастыруға болады? Шыққан сандарды бұтақтар әдісі арқылы көрсет.
2. 0, 1 және 2 цифрларынан: а) цифрлары қайталанбайтын, б) цифрлары қайталанатын қанша үштаңбалы сандар алуға болады? Орындалуын бұтақтар арқылы көрсет.
3. 1 және 2 цифрларынан қанша үштаңбалы сан құрастыруға болады? Шыққан сандарды бұтақтар әдісі арқылы көрсет.
4. 3694 санының цифрларынан қанша төрт таңбалы тақ сандар құрастыруға болады? Мұнда әрбір цифр бірден артық қолданылмауы керек.
5. 0, 1, 2 цифрларынан қанша үш таңбалы қайталанбайтын сан құрастыруға болады.
6. 1, 2, 3 цифрларынан неше әдіспен екітаңбалы сан құрастыруға болады? Шыққан сандарды бұтақтар әдісі арқылы көрсет.
7. 1, 2, 3 цифрларынан цифрлары қайталанбайтын қанша үш таңбалы сан құрастыруға болады.
8. 0, 1, 2, 3 цифрларынан цифрлары қайталанбайтын қанша екі таңбалы сан құрастыруға болады.
9. 0, 1, 2 цифрларынан қанша төрт таңбалы сан құрастыруға болады?
10. Цифрлары қайталанбайтын тақ цифрлардан қанша төрт таңбалы сан құрастыруға болады.
11. 0, 3, 5 цифрларынан қайталанбайтын қанша үш таңбалы сан құрастыруға болады.
12. Кассадан ақша алуға бірмезгілде 4 адам келді. Кезекке неше әдіспен тұруларына болады.
13. 1) Математика, 2) Статистика, 3) Призма, 4) Алгоритм, 5) Этика сөздеріндегі әріптерді ауыстыра отырып қанша әртүрлі (мағынасыз) сөздер құрастыруға болады.
14. Телефонның нөмірін теріп тұрып абонент соңғы екі цифрды ұмытып қалды. Осы цифрларды неше әдіспен теруге болады?
15. Сыныпта 30 оқушы бар. Күнде екі баладан кезекші болу керек. Оқу жылы бойы екі оқушы бірге екі рет кезекшілікті атқармайтындай кесте құруға бола ма?
16. Бір адамда 7 кітап, ал екінші адамда 9 кітап бар. Олар бір-бірімен екі кітапты неше әдіспен ауыстыруларына болады?
17. Телефон нөмірін теріп тұрып абонент соңғы екі цифрды ұмытып қалды, тек олар әртүрлі екенін біледі. Бұл цифрларды ол неше әдіспен тере алады.
18. Нөмірі үш әртүрлі тақ саннан тұратын машина іздестірілуде. Мұндай машиналар саны қанша болады?
19. Егер подъездің (кіреберіс) есігі 0-ден 9-ға дейін нөмірленген үш әртүрлі кнопканы бір мезгілде басқанда ашылатын болса, онда оны ашудың неше әдісі болады.
20. Корпорацияның директоры 10 университет бітірушінің жұмысқа тұру туралы арызын қарастырады. Бірлестіктің бір кәсіпорынында 3 әртүрлі бос орын бар. Бұл бос орындарды директор неше әдіспен толтыра алады?
21. Телефон нөмірін теріп тұрып абонент соңғы үш цифрды ұмытып қалды. Бұл цифрларды неше әдіспен алуға болады?
22.Топта 20 студент бар, оның 15-і қыз бала. Төрт ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.