Жұлдыздардың тәуліктік параллельдері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 30 бет
Таңдаулыға:

КІРІСПЕ
I. СФЕРАЛЫҚ ЖӘНЕ ПРАКТИКАЛЫҚ АСТРОНОМИЯ НЕГІЗДЕРІ
1.1. Жұлдызды аспан. Аспан сферасы.
1.2. Әртүрлі географиялық ендіктегі аспан шырақтрының көрнекілік қозғалысы.
1.3. Жергілікті, белдеулік және бүкіләлемдік уақыт.
1.4. Күн жүйесіндегі планеталардың қозғалыс заңдары.
II. КОСМОЛОГИЯ ЖӘНЕ КОСМОГОНИЯ НЕГІЗДЕРІ
2.1. Жұлдыздар әлемі
2.2. Жұлдыздар эволюциясы
2.3. Біздің галактика
2.4. Ғалам
III. ОРТА МЕКТЕП ФИЗИКА КУРСЫНДАҒЫ ФСТРОНОМИЯ НЕГІЗДЕРІН ОҚЫТУДЫҢ ӘДІСТЕМЕЛІК ЕРЕКШЕЛІКТЕРІ
3.1. Астрономия негіздерін оқытудың рөлі және әдістемелік ерекшеліктері
3.2. Ғалам құрылымы, космогония тақырыптарын оқыту әдістемесі
3.3. Мектеп физика курсында астрономия негіздерін сабақтан тыс оқытудың формалары
3.4. ҚМЖ

I. СФЕРАЛЫҚ ЖӘНЕ ПРАКТИКАЛЫҚ АСТРОНОМИЯ НЕГІЗДЕРІ

1.1. Жұлдызды аспан. Аспан сферасы.

Адамдар түнгі аспанды алғаш рет картаға түсіре бастағанда, аспандағы объектілерді орналастырудың стандартты, әмбебап әдісі қажет болды. Жұлдыздар бір-біріне қатысты аспанда тұрақты позицияларды алатын сияқты болғандықтан, жағдайды түсінудің ыңғайлы тәсілі үлкен сфераның ортасына орналастырылған жерді елестету болар еді.
Жұлдызды аспан - самсаған сансыз шырақтармен көмкерілген көк күмбез. Сократтың шәкірті, Аристотельдің ұстазы әйгілі Платон аспан күмбезін былай елестеткен: Әлем жәй ғана күмбез емес. Ол - мінсіз де кемел күмбез. Жаратушы оның бетін мұнтаздай жылтыр етуге қамқорлық жасады және бұл себепсіз де емес еді.... Еуразия кеңістігін алып жатқан апайтөс Ұлы Дала өкілдері және олардың бірі - қазақ халқы өкілдерінің ертегілері мен әпсаналарында Платон суреттеген күмбезді жеті қат, кейде тоғыз қат көк деп пайымдаған. Есте жоқ ескі заманда қалыптасқан мұндай пайымдау Платонша айтқанда себепсіз де емес еді. Расында да, Бұқар жыраушы Ай нұрын ұстап мініп, жұлдыз аралап... алысқа бармай-ақ, бергі Күн жүйесіне зер салсақ, ондағы шырақтардың біреуі бері, біреуі әрі жеті-тоғыз қабаттан тұратыны белгілі. Солардың бірі - Абай жырлаған сәулесі суда дірілдеген, желсіз түнде жарық Ай - бізге ең жақын жалыны жоқ аспан шырағы. Екіншісі - біздің ең жақын жалындап жанып тұрған жұлдыз - Күн. Олардан басқа Жерде тұрып қарусыз көзбен көруге болатын әртүрлі орбиталар бойымен Күнді айнала қозғалатын жалынсыз бес планета: Меркурий (қазақша Кіші шолпан немесе Балапан), Шолпан, Марс (Қызыл жұлдыз), Юпитер (Есекқырған) және Сатурн.
Жердің екі жартышарында жай көзбен көруге болатын 6 мынадай шырақтардың барлығы дерлік жұлдыздар болып табылады. Өткір көзді адан түнгі Айсыз ашық аспанда көк күмбезінің өзі тұрған жартышарында 3 мың жұлдызды көре алады. Жердің екінші жартышарында тұрған адам да жай көзбен сонша жұлдыздарды бақылай алады. Алғаш рет жұлдыздар тізімін біздің дәуірге дейін II ғасырда ежелгі элладалық (грекиялық) астроном Гиппарх жасады. Оның тізіміне Птоломейдің кейінгі толықтыруларымен 1022 шырақ енгізілді. Бірте-бірте жай көзге көрінетін шырақтар саны 6 мыңға жеткізілді. Олардың ішінде жиі аталатын 300 жұлдыздың төл атауларының 15%-ы грек, 5%-ы латын, 80%-ы араб тілінде аталады. Араб тіліндегі жұлдыздар атауын беруге мұсылман ғалымдары деп аталып кеткен Орталық Азия халықтарынан шыққан ұлы ғұлама астрономдар да зор үлес қосты.
Қазіргі Жер бетіндегі және ғарыш кеңістігіне ұшыраған телескоптарда соңғы жүз жылда тіркелген мәліметтер бойынша тек Біздің Галактиканың өзінде 200 миллиардтан жұлдыздардың бар екендігі анықталды. Басқа Галактикалардағы жұлдыздар саны да ондаған, жүздеген миллиардтарды құрайды. Телескоптарда тіркелген жеке Галактикалардың саны да миллиардтан асады. Міне, жұлдызды аспанның қазіргі ғылыми астрономияда анықталған галактикалық құрылымдық қабаттары мен қатпарлары осындай.
Жұлдыздардың көрінерлік жарықтылығы бірдей емес: біразы жарқырап, самалдай самсап көрінсе, біразы көзге әрең шалынады. Осыған орай Гиппарх көрнекілік жұлдыздық шама деген ұғым енгізіп, өз тізімінде шырақтарды 6 топқа жіктеген болатын. Солардың ішінде ең жарық жұлдыздары (мысалы, қазақтар Сүмбіле деп атайтын Сириусты) бірінші топқа, ал ең солғындарын алтыншы топқа енгізген еді.
1603 жылы неміс астрономы Игоанн Байер әр шоқжұлдыздағы жұлдыздардың жарықтылық деңгейлерін грек әріптерінің ретімен көрсетуді ұсынды. Мысалы, ең жарық жұлдыз α әрпімен, одан кейін β т.с.с. әріптерімен белгіленеді.
Қазіргі кезде астрономдар ағылшын ғалымы Норман Погсон XIX ғасырда ұсынған көрнекілік жұлдыздық шама өлшемдерін қолданады. Бұрдай өлшемдер бойынша көрнекілік жұлдыздық шама 5 топқа бөлінеді де, әр топтағы жұлзыздар шамасын бір-бірінен 5100≈2,512 есеге өзгеріп отырады. Көрнекілік жұлдыздық шаманы латынның magnitude - шама сөзіндегі бірінші тұрған m әріпімен белгіленеді.
Астрономияда жұлдыздың жарқырауы деп аталатын шама да көрнекілік жұлдыздық шама өлшемінде беріледі. Жұлдыздардың жарқырау көрсеткіші көрнекілік жұлдыздық шама бойынша теріс немесе оң сандармен де, бүтін немесе бөлшек сандарымен де беріле береді. Мысалы, ең жарық жұлдыз Сүмбіленің көрнекілік жұлдыздық шамасы m = - 1,56; Күннің көрнекілік жұлдыздық шамасы m = - 26,6; Айдың көрнекілік жұлдыздық шамасы m = - 17,7.
Аспан шырақтарының көрнекілік жұлдыздық шамасымен өлшенген жарқырауы олардың шын жарықтылығын бере алмайды. Өйткені тым алыстағы жарықтылығы күшті шыраққа қарағанда, көзге жақын орналасқан шырақ жарқырап көрінуі мүмкін. Сондықтан шырақтардың орналасу қашықтықтарына қарай олардың шын жарықтылығын ескеру үшін М әрпімен белгіленетін абсолюттік жұлдыздық шама деген түсінік енгізілген. Бір обсолюттік жұлдыздық шама деп бақылаушыдан 10 парсек қашықтықта орналасқан шырақтың жарықтылығын айтады (мұндағы 1 парсек жарықтың бір жылда жүріп өткен жолы). Бұндай өлшем бойынша Сүмбіленің абсолюттік жұлдыздық шамасы M = +1,41; Күннің абсолюттік жұлдыздық шамасы M = +4,8 т.с.с. (форзацтағы қосымшаны қараңдар).
Ежелгі халық астрономиясында көзге айқын көрінетін шырақтарды шоқжұлдыз шоғырларына бекітілген.
Шоқжұлдыз деп аспанның белгілі бір жұлдыздыр шоғыры енетін шегарасы анықталған бөлігін айтады.
Жұлдыздардың шоғырлануына қарай аспан күмбезін бөліктерге бөлу тәсілі ғылыми астрономияда да қолданыс тапты. Осылайша аспан күмбезі бірнеше бөліктерге бөлініп, бұл бөліктерде 88 шоқжұлдыз орналасқан. Бұлардың ішінен 12 шоқжұлдызға халық астрономиясы ерекше мән беріп, орналасу пішіндеріне қарай оларға әртүрлі жануарлардың немесе ертегі-аңыздардың кейіпкерлерінің аттарын беріп ортырған. 12 щоқжұлдызға айрықша мән берудің себебі мынада: ескі түсінік бойынша Жердің айнала қозғалатын Күн аспан күмбезінде бір жылда бір рет әрбір 12 шоқжұлдыздың тұсынан өтеді. Зодиакальдік шоқжұлдыздар деп аталып кеткен мұндай жұлдыздар шоғырлана мыналар кіреді: жыл басы наурызға сәйкес келетін тоқты айы (21.03-20.04), торпақ айы (21.04-21.05), егіздер айы (22.05-21.06), шаян айы (22.06-23.07), арыстан айы (24.07-23.08). бикеш айы (24.08.-23.09), таразы айы (24.09-23.10), сарышаян айы (24.10-22.11), мерген айы (23.11-21.12), тауешкі айы (22.12-20.01), суқұйғыш айы (21.01-19.02), балықтар айы (20.02-20.03). Осындай пайымдауға сүйеніп, жыл мезгілдерін және уақытты көрсететін күнтізбелер жасалған. Алайда бір жылда Күн Жерді емес, Жер Күнді айналатыны белгілі болғанан кейін де, ертеде жасалған мұндай күнтізбелер өз құндылығын жойған жоқ. Өйткені жыл мезгілдері мен күнтізбелік уақыттарға айтарлықтай өзгерістер енгізудің қажеттілігі тумады. Осылайша Жердің екі жартышарларының үстіндегі күмбездерін қосып, халық астрономиясы мен ғылыми астрономияны біріктіретін аспан сферасы деген ұғым қалыптасты.
Аспан сферасы деп радиусын шексіз үйкелтуге болатын, центрге кеңістіктің кез келген нүктесінде орналсқан сфераны айтады.
Аспан сферасының О центрі ретінде бақылаушының тұрған орнын, телескоптың Жердегі немесе ғарыштағы орнын, Жер центірін т.с.с. алуға болады. Жердің өз өсіне батыстан шығысқа қарай айналуына байласынты аспан шырақтары солтүстік жартышарда Жердің шығыстан батысқа қарай айналғандай болып көрінеді. Сондықтан да аспан сферасына проекцияланған аспан шырақтарының кеңістіктегі орны өзгеріп отырады.
Аспан сферасын сипаттайтын ең баста элементтерге мыналар жатады:
Бақылаушы вертикалі - аспан сферасының центірі арқылы өтетін, әрі бақылаушы тұрған нүктедегі тіктеуіштің бағытымен бағыттас тік сызық.
Зенит Z - бақылаушының қақ төбесіндегі аспан сферасындағы нүкте.
Надир Z` - зенитке қарама-қарсы аспан серасындағы нүкте.
Ақиқат горизонт (көкжиек) - бақылаушы вертикаліне (тік сызыққа) перпендикуляр дөңгелек.
Әлем өсі (РР`) - аспан сферасының айналу өсіне өтетін сызық.
Әлем полюстері - аспан сферасының әлем өсімен қиылысу нүктелері.
Аспан экваторы - жазықтығы әлем өсіне перпендикуляр болатын аспан сферасының бетіндегі шеңбер.
Аспан меридианы немесе бақылаушы меридианы - әлем полюстері және зенит пен адир арқылы өтетін аспан сферасы бетіндегі үлкен дөңгелек.
Солтүстіктің және оңтүстіктің нүктелері (N және S) - аспан меридианының ақиқат горизонтпен (көкжиекпен) қиылысу нүктелері.
Шығыстың және батыстың нүктелері (E және W) - аспан экваторының ақиқат горизонтпен (көкжиекпен) қиылысу нүктелері.
Талтүстік сызығы - ақиқат горизонттың бетіндегі солтүстік пен оңтүстіктегі нүктелерді қосатын түзу сызық.
Шырақ вертикалі (қысқаша вертикаль) - аспан сферасы бетіндегі зенит, надир және шырақ (М) арқылы өтетін доғалық сызық.

Жұлдыздар осы "аспан сферасының" бетінде тұрақты позицияларды алады және жер оның ішінде айналады. Бұл нақты өмірде олай емес екені анық, бірақ бұл жақсы үлгі, өйткені бәрі біздің көзқарасымыз бойынша осылай көрінеді.
Жер осы сфераның ішінде айналады, бірақ, әрине, бізге аспан сферасы Жермен бірдей осьтің айналасында айналатын сияқты. Егер жер осінің сызығы шексіздікке дейін созылса, оның аспан сферасымен қиылысатын нүктесі аспан полюсі деп аталады.
Егер біз жерді қозғалыссыз қабылдайтын болсақ, онда барлық жұлдыздар осы нүктенің айналасында айналады. Біз солтүстік жарты шарда аспан полюсінде азды-көпті дәл орналасқан Жұлдыз, Солтүстік жұлдыз болғаны үшін бақыттымыз. Егер сіз ашық түнде шығып, бірнеше сағат ішінде белгілі бір шоқжұлдызға бірнеше рет қарасаңыз, оның аспан полюсінің айналасында айналатынын байқайсыз.
Мұны қорытындылай келе, Жердің кез келген нүктесіндегі аспан экваторы мен Зенит (яғни ауытқу) арасындағы бұрыш сол нүктедегі ендікке тең. Бұл бізді пайдалы нәтижелерге жетелейді:
ИІЛУ
Енді жердің экваторы шексіздікке дейін созылатынын елестетіп көріңіз, аспан сферасындағы сәйкес Нүкте-аспан экваторы. Жердегі полюс пен экватор арасындағы бұрыш дұрыс бұрыш сияқты, аспан сферасына да қатысты. Осы себепті аспан экваторындағы нүктелер 0 ° ауытқуы бар, ал аспан полюсі 90 °ауытқуы бар деп айтылады.
Назар аударыңыз, ауытқу полюстің ендігі 90 °, ал экватордың ендігі 0 °болатын жердегі ендікке ұқсас. Әрине, біз сондай - ақ Жердегі ендікке сәйкес келетін 10°, 20°, 30 ° және т.б. ауытқулар арасындағы сызықтарды елестете аламыз және экватордың оңтүстігіндегі сызықтардың теріс ауытқулары бар екенін атап өтуге болады (мысалы, -76 ° - 76 ° оңтүстік ендік).
Градус фракциялары доғалық минуттармен (градусқа 60 доғалық минут) және секундтармен (доғалық минутқа 60 доғалық секунд) өлшенеді. Осылайша, сіз -7 ° 27' 03" деп белгіленген белгілі бір ауытқуды көре аласыз, бұл 7 градус 27 минут 3 секунд Оңтүстік ендікті білдіреді, бұл аспан экваторынан оңтүстікке қарай 7 жарым градустан аз.
Шындығында, доғалық секундтар алаңдату үшін тым кішкентай, ең жақын жарты градусқа дейін дөңгелектеу әдетте жеткілікті дәлірек.
Ауытқу мен ендік арасындағы байланыс шынымен де маңызды, өйткені ол теңізшілерге мыңдаған жылдар бойы өздерінің ендіктерін анықтауға мүмкіндік берді, бірақ мен бұған кейінірек ораламын.
ОҢҒА КӨТЕРІЛУ
Әлбетте, біз нүктелерді тек бір координатамен белгілей алмаймыз, нүктені толық анықтай алу үшін бойлық жерде қажет болған сияқты, басқа жиынтық қажет. Оңға көтерілу (РА) - бойлықтың аспан эквиваленті. Бойлықтың Табиғи мәні жоқ сияқты, Лондондағы Гринвич обсерваториясында ерікті түрде орталықтандырылған сияқты, Ra Овеннің бірінші нүктесінде нөлге тең деп анықталды.
Жер айналатындықтан, жұлдыздар айналатын сияқты, бірақ қозғалыс болмағандықтан, Солтүстік-Оңтүстік ауытқу сызықтары өзгеріссіз қалады - сондықтан олар маңыздырақ.
Жұлдыздар шығыстан батысқа қарай айналатын сияқты болған кезде, РА сызықтары қозғалады-олар күніне бір толық айналым жасайды (шын мәнінде, күн сайын Жер Күнді шамамен 1 ° айналдыратындықтан, сәл үлкенірек, бірақ бұл күн сайын елемеуге жеткілікті аз). Бұл белгілі бір жұлдыздың сағатына 15 ° қозғалатынын білдіреді.
Сонымен, біз оңға көтерілуді сағатпен өлшеуге ыңғайлы, мұнда 15 градус сағат, ал 360 градус 24 сағат. Бұл уақыт одан әрі минуттар мен секундтарға бөлінеді (доғалық минуттармен және доғалық секундтармен шатастырмау керек, бұл бірдей емес) уақытты бөлумен бірдей, яғни сағат 60 минутқа тең, минут 60 секундқа тең және т. б.
Егер сіз жұлдызға телескоп арқылы қарасаңыз айталық, 50 ° және 0 сағаттық ra ауытқуымен, 1 сағаттан кейін сіз 1 сағаттық RA-ға, содан кейін 2 сағаттан кейін 2 сағаттық RA-ға және т.б. қарайсыз. Шындығында, 3 сағат 56 минут 12 секундтан кейін сіз 3 сағат 56 минут 12 секундта оңға көтерілуді көресіз делік!
Енді бізде екі координат бар, біз аспан сферасының бетіне кез-келген нүкте қоя аламыз. Мысалы, Орион тұмандығының координаттары -5° 27 ' желтоқсан, 5 сағат 35 минут 24 секунд. Ра Андромеда галактикасының координаттары 41° 16 ' желтоқсан, 0 сағат 42 минут 42 секунд.Бұл нысандар қозғалатын болып көрінгенімен, олардың координаттары бекітілгенін түсіну маңызды.
Бұл біз тұрған жерден қалай көрінеді? Бұл сіздің жердегі жағдайыңызға байланысты.
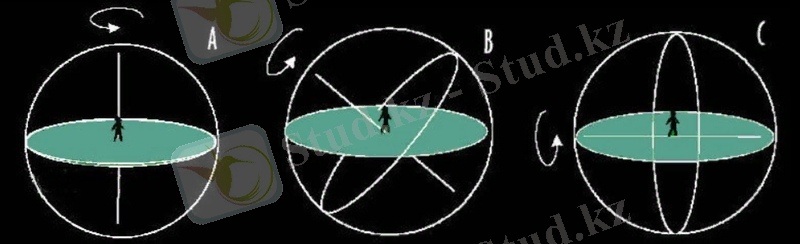
Бақылаушы А жер полюсінде тұрған кезде оның үстінде аспан полюсі бар. Жұлдыздар біздің бақылаушымыздың айналасында айналады. Аспан экваторы көкжиекте - ол жұлдыздарды тек солтүстік жарты шарда көре алады.
C бақылаушысы жердің экваторында орналасқан аспан экваторына ие. Аспан полюстері көкжиектің қарама-қарсы ұштарында орналасқан, ал жұлдыздар тікелей шығыстан батысқа қарай доға құрайды. Осы жерден сіз барлық жұлдыздарды көре алатын жалғыз ендік, өйткені Солтүстік және оңтүстік жарты шарлардың тең саны көрінеді, ал жер бұрылған кезде аспан сферасындағы барлық позициялар бір нүктеде көрінеді.
Мен В бақылаушысына соңғы болып келдім,өйткені біздің көпшілігіміз оның позициясында. Біздің бақылаушы 45 ° ендікте, бірақ бұл полюс пен экватордың екі шеткі нүктесі арасындағы кез келген жерге қатысты. 90 ° ендіктегі бақылаушының дәл үстінде 90 ° ауытқуы болды (оның зенитінде), ал 0 ° ендіктегі бақылаушының Зенитте 0 ° ауытқуы болды.

Геометриядан бұл бұрышты көру оңай p аспан полюсінің көкжиектен биіктігі бұрышқа тең l, ендік. Бұл навигацияда өте маңызды, өйткені ол ежелгі теңізшілерге аспан полюсінің биіктігін өлшеу арқылы ендіктерін анықтауға мүмкіндік берді (Солтүстік жарты шарда бұл оңай, өйткені Полярис, жарық жұлдыз полюске жеткілікті жақын).
Сондықтан, егер сіз бейтаныс елдің жылан батпақтарында адасып қалсаңыз немесе кеме апатқа ұшырап, адам тұрмайтын аралға тасталсаңыз, сіз өзіңіздің ендігіңізді-аспан полюсінің биіктігін қалай анықтау керектігін білесіз.
Сондай-ақ, аспан экваторы қай жерде болсаңыз да, әрқашан Шығыс пен Батыста көкжиекті дәл кесіп өтетінін ескеріңіз. Аспан экваторын табу үшін алдымен полюсті табыңыз. Бір жағына 90°, содан кейін екінші жағына қараңыз, бұл шығыс пен Батыс. Содан кейін қарама-қарсы жаққа қарау үшін 180 ° бұрылыңыз. Бұл нүктеде (полюске қарама - қарсы) экватор көкжиектен 90 ° биіктікте орналасқан-сіздің ендігіңіз және ол шығыстан, сол нүкте арқылы, содан кейін батыста көкжиекпен қайта кездесу үшін төмен қарай өтеді. Егер сіз аспан полюсі мен экватордың қай жерде тұратындығын білсеңіз, бұл сізге көмектеседі. Енді сіз жұлдыздардың қалай қозғалатынын көре аласыз: аспан экваторының сызығынан кейін, полюстің айналасында.
Егер сіз осы демонстрацияны көргіңіз келсе, мына суреттерді қараңыз баяу қозғалатын фотосуреттер әлемнің түкпір-түкпірінен алынған, жұлдыздардың көрінетін қозғалысын көрсетеді. Аспан полюсінің орналасуы ендікке байланысты қалай өзгеретініне назар аударыңыз, мысалы, Килиманджаро Тауында оңтүстікке қарай 3 ° (оңтүстік) полюс көкжиектен 3 ° жоғары.

1.2. Әртүрлі географиялық ендіктегі аспан шырақтрының көрнекілік қозғалысы.

Бақылаушылар шар пішінді Жер бетінде орналасқандықтан, жұлдызды аспан көрінісі оның тұрған орнының географиялық ендігіне байланысты әртүрлі болады. Географиялық ендік мәніне байланысты шырақтардың тәуліктік параллельдері көкжиекке қатысты әртүрлі бұрышпен орналасқан.
Жердің солтүстік Р полюсінде бақылаушыға аспан сферасының тек солтүстік жартышары, ал оңтүстік полюсте оның оңтүстік жарты шары ғана көрінеді. Жер полюстерінде дүние өсі тік сызық бойымен сәйкес келеді. Жұлдыздардың тәуліктік параллельдері көкжиекке параллель орналасады (сурет 1), яғни барлық жұлдыздар батпайды және тумайды.

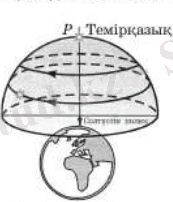
Сурет 1. Жұлдыздардың тәуліктік параллельдері

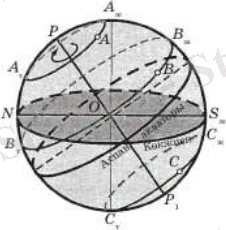
Бақылаушы солтүстік полюстен экваторға сапар шеккенде, жұлдызды аспан көрінісі өзгеріп отырады. Дүниенің солтүстік полюсінің зениттен бұрыштық қашықтығы біртіндеп өседі. Осыған орай жұлдыздардың тәуліктік параллельдерді көкжиекке көлбеу орналасады. Сөйтіп, аспан экваторы мен көкжиек жазықтықтарының арасындағы бұрышта өсетін болады, соның салдарынан аспан сферасының экваторға таяу бөлігіндегі жұлдыздар көкжиектен шығып, көкжиекте бататын болады, мысалы, В жұлдызды (сурет 2).
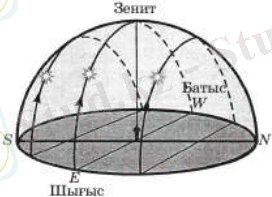
Бақылаушы Жер экваторына жеткенде, дүние полюстері көкжиекке (оның тура солтүстік және оңтүстік нүктелеріне) дәл келеді. Ал аспан экваторы зенит арқылы өтеді. Жұлдыздардың қозғалысы аспан экваторына параллель болғандықтан, олар шығыс көкжиектен оған тікбұрыш жасай көтеріліп, сол қалпында батыс көкжиекке төмендейді (сурет 3). Экватордағы бақылаушы аспаннан оның екі жартышарының барлық жұлдыздарын көре алады.

Сурет 2 Сурет 3

Шырақтардың қозғалыс барысында көкжиектен ең жоғары және ең төмен орналасуы олардың шарықтауы деп аталады. Шарықтың көкжиектен ең биік және ең төмен оналасуын тиісінше жоғарғы және төменгі шарықтауы дейді. Сурет 2-де жұлдыздардың орта ендікте бақыланатын тәуліктік қозғалысының траекториялары көрсетілген. Мұнда А жұлдызы - батпайтын жұлдыз. Оның жоғарғы (Аж) және төменгі (Ат) шарықтауы көкжиек үстінде болса, В жұлдызының тек жоғарғы шарықтауы ғана көкжиек үстінде болады. Ал С жұлдызы - бұл орында тумайтын жұлдыз. Оның жоғарғы және төменгі шарықтауы көкжиек астында болады. Осылайша шырақтың көкжиектік координаталары тәулік ішінде үздіксіз өзгеріп отырады.
Күнделікті қозғалыс кезінде шамдар аспан меридианын екі рет кесіп өтеді. Аспан меридианының қиылысу сәті шамның шарықтау шегі деп аталады. Жоғарғы шарықтау шегі кезінде жарық көкжиектен ең жоғары биіктікке жетеді. 2.8-суретте жоғарғы шарықтау шегіндегі шамның орны көрсетілген. Егер біз солтүстік ендіктерде болсақ, онда әлем полюсінің биіктігі көкжиектен жоғары (PON бұрышы): hр = φ. Содан кейін Көкжиек (NS) мен аспан экваторы (QQ1) арасындағы бұрыш 180° - φ - 90° = 90° - φ болады. Егер жарық көкжиектің оңтүстігінде шарықтаса, онда шамның биіктігін білдіретін MOS бұрышы М шарықтау шегінде екі бұрыштың қосындысы болып табылады: Q1QS және MOQ1. Біз олардың біріншісінің шамасын жаңа ғана анықтадық, ал екіншісі-m шамының δ-ге тең ауытқуынан басқа ештеңе емес.

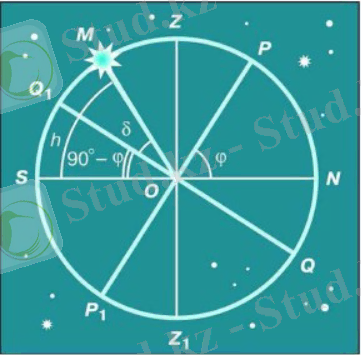
Осылайша, біз Оңтүстік көкжиектен жоғары шарықтау шегіндегі шамның биіктігін оның ауытқуымен және бақылау орнының географиялық ендігімен байланыстыратын келесі формуланы аламыз:
h = 90° - φ + δ.
Егер δ φ болса, онда жоғарғы шарықтау шегі биіктікте Солтүстік көкжиектен жоғары болады
h = 90° + φ - δ
Бұл формулалар Жердің оңтүстік жарты шарына да қатысты екенін көрсетуге болады. Шамның ауытқуын біле отырып және бақылаулардан оның шарықтау шегіндегі биіктігін анықтай отырып, бақылау орнының географиялық ендігін білуге болады.
Біз қиялдағы саяхатты жалғастырамыз және географиялық ендігі 0°болатын орта ендіктерден экваторға барамыз. Жаңадан алынған формуладан көрініп тұрғандай, мұнда Әлем осі көкжиек жазықтығында орналасқан, ал аспан экваторы зенит арқылы өтеді. Экваторда бір күн ішінде барлық шамдар көкжиектен жоғары болады (сурет. 2.9).

1.3. Жергілікті, белдеулік және бүкіләлемдік уақыт.

Үлкен және кіші уақыт аралықтарын өлшеу үшін астрономиялық құбылыстармен тығыз байланысты табиғи бірліктер қолданылады. Уақыттың негізгі табиғи бірліктері - тәулік, ай және жыл. Бұлардың алғашқысы күн мен түннің алмасуына, екіншісі Ай жүзінің (фазасының) өзгеруіне, ал соңғысы жыл маусымдарының ретті түрде алмасуына байланысты.
Тәулік дегеніміз - Жердің аспандағы белгілі бір санақ денесіне қатысты өз өсіне толық бір айналым жасауға кететін уақыт аралығы. Мұндай дене ретінде Күн немесе кез келген жұлдыз алынуы мүмкін. Олай болса, біз күн тәулігі және жұлдыз тәулігі деген ұғымдарды ажырата білуіміз қажет.
Күн шарығының (дискісінің) орталық нүктесінің жоғарғы шарықтау сәті нақты талтүс деп, ал төменгі шарықтауы нақты түн ортасы деп аталады.
Күннің екі аттас шарықтау аралығы нақты күн тәулігі деп аталады. Бірақ мұндай тәуліктің ұзақтығы жыл бойы тұрақты болмайды. Бұл Күннің көрінерлік қозғалысы экватор емес, эклиптика бойымен өтуінен туындайды. Сондықтан күнделікті өмірде ұзақтығы тұрақты 24 сағ болатын орташа күн тәулігі пайдаланылады.
Күн тәулігінің басы түн ортасынан, яғни Күннің төменгі шарықтауынан басталады.
Күннің меридан арқылы өту сәті, бақылаушы орнының географиялық бойлығына тәуелді. Күннің жергілікті меридиан арқылы өту сәті бізге жергілікті орнының күн уақытын береді. Бұл уақыт тек берілген географиялық меридианда ғана қолданылатындықтан, күнделікті өмірде белдеулік уақытты қолдану ыңғайлы. Бұл үшін Жер беті полюстерді қосатын сызықтар көмегімен 24 сағаттық белдеулерге бөлінген. Әр сағаттық белдеу бойлық бойымен 15°-қа созылады. Әр белдеудің ішінде оның орталық меридианындағы орташа күн уақыты осы аймақтың белдеулік уақытты ретінде алынады.
Гринвич обсерваториясы (Ұлыбританияда) орналасқан меридиан нөлінші меридиан ретінде қабылданған және ол белдеу нөлінші сағаттық белдеу болып табылады. Гривич меридианындағы жергілікті орташа күн уақыты бүкіләлемдік уақыт ретінде қабылданған. Бірінші сағатқа (1-сағ) сәйкес келетін белдеудің (n = 1) орталық меридианы Гринвич меридианынан 15° шығысқа қарай орналасқан. Басқа сағат белдеулерінің де бастапқы меридиандары осылай анықталады. Қазақстанның аумағы арқылы Гринвичтен есептегенде 4-сағаттық (мысалы, Атырау) және 5-сағаттық (мысалы, Өскемен) белдеулер өтеді.
Бүкіләлемдік уақытты (Т0) және берілген орынның белдеуінің реттік санын (n) біле отырып, белдеулік уақытты табу оңай:
Tn=T0+n.
1930 ж. көктемде үкімет декреті бойынша КСРО аумағындағы декреттік уақыт енгізілді: барлық сағаттық белдеулерде сағат тілі тұрақты түрде бір сағатқа ілгері жылжытады. Кейбір елдерде декреттік уақытты жаз айларында 1 сағ ілгері жылжыту қабылданған.
Алматы және Астана уақыты (5-сағаттық белдеу) бүкіләлемдік уақыттан 6 сағат алда.
T5=T0+n+1=T0+6 сағ.
Географиялық бойлығы λ болатын Tλ жергілікті орташа күн уақыты бүкіләлемдік уақытқа сол бойлықтың уақыт уақыт бірлігіндегі мәнін қосу арқылы анықталады:
Tλ=T0+λ.
Берілген географиялық меридианда өлшенген уақыт осы меридианның жергілікті уақыты деп аталады. Бір меридиандағы барлық орындар үшін көктемгі күн мен түннің теңелу нүктесінің сағат бұрышы (немесе күн немесе орташа күн) бір сәтте бірдей. Сондықтан бүкіл географиялық меридианда жергілікті уақыт (жұлдызды немесе күн) бір сәтте бірдей.
Егер екі жердің географиялық бойлық айырмашылығы болса, онда Шығыс жерде кез-келген шамның сағаттық бұрышы сол шамның батыстағы сағаттық бұрышынан үлкен болады. Сондықтан бір физикалық сәтте екі меридиандағы кез-келген жергілікті уақыттың айырмашылығы әрқашан сол меридиандардың бойлық айырмашылығына тең, сағаттық өлшеммен (уақыт бірлігінде)көрсетілген:
s1-s2=λ1-λ2
T1-T2=λ1-λ2
Тікелей астрономиялық бақылаулардан осы бақылаулар жасалған меридианның жергілікті уақыты алынады.

1.4. Күн жүйесіндегі планеталардың қозғалыс заңдары.
Күн жүйесінің құрылымы туралы идеяларды қалыптастыруда Иоганн Кеплер ашқан және олардың қазіргі мағынасында алғашқы жаратылыстану-ғылыми заңдар болған планеталардың қозғалыс заңдары да маңызды рөл атқарды. Кеплердің жұмысы сол дәуірдің механикасы туралы білімді динамика заңдары және кейінірек Исаак Ньютон тұжырымдаған тартылыс заңы түрінде жалпылауға мүмкіндік берді. Көптеген ғалымдар XVII ғасырдың басына дейін.аспан денелерінің қозғалысы біркелкі болуы керек және "ең жақсы" қисық -- шеңбер бойымен жүруі керек деп есептеді. Тек Кеплер бұл алалаушылықты жеңіп, планеталық орбиталардың нақты формасын, сондай-ақ планеталардың Күнді айналып өту жылдамдығының өзгеру заңдылығын орната алды.
Кеплер өзінің ізденісінде Пифагор айтқан "әлемде Сан билік етеді" деген сенімнен туындады. Ол планеталардың қозғалысын сипаттайтын әртүрлі шамалар -- Орбита өлшемдері, айналу кезеңі, жылдамдық арасындағы қатынастарды іздеді. Кеплер іс жүзінде соқыр, таза эмпирикалық түрде әрекет етті. Ол планеталардың қозғалыс сипаттамаларын музыкалық гамма заңдылықтарымен, сипатталған және орбитаға жазылған планеталардың көпбұрыштардың қабырғаларының ұзындығымен және т. б. салыстыруға тырысты.
Кеплерге планеталардың орбиталарын құру, планетаның аспан сферасындағы орнын көрсететін экваторлық координаттар жүйесінен оның Орбита жазықтығындағы орнын көрсететін координаттар жүйесіне өту қажет болды. Ол Марс планетасының өзінің бақылауларын, сондай-ақ оның мұғалімі Тихо Брахе жүргізген осы планетаның координаттары мен конфигурацияларының көпжылдық анықтамаларын пайдаланды.
Кеплер жердің орбитасын (бірінші жуықтауда) бақылауларға қайшы келмейтін шеңбер деп санады. Марс орбитасын құру үшін ол 3.5-суретте көрсетілген әдісті қолданды.
Планетаның қарама -- қайшылықтарының бірі кезінде Марстың көктемгі күн мен түннің теңелу нүктесінен бұрыштық қашықтығын білейік -- оның αT1M1 бұрышымен өрнектелген α1 оңға көтерілуі, мұндағы T1 -- жердің сол кездегі орбитадағы орны, ал M1-Марстың орны. Әлбетте, 687 күннен кейін (бұл Марстың жұлдызды айналу кезеңі) планета өз орбитасының дәл сол нүктесіне келеді. Егер сіз осы күнге Марстың оңға көтерілуін анықтасаңыз, онда 3.5-суреттен көріп отырғаныңыздай, планетаның кеңістіктегі орнын, дәлірек айтқанда, оның орбиталық жазықтығында көрсетуге болады. Бұл кезде жер T2 нүктесінде, сондықтан Мар T2M1 бұрышы Марстың оңға көтерілуінен басқа ештеңе емес -- α2. Марстың бірнеше басқа қарсыластары үшін осындай операцияларды қайталай отырып, Кеплер көптеген нүктелер алды және олардың бойымен тегіс қисық сызып, осы планетаның орбитасын жасады.

Алынған нүктелердің орналасуын зерттей отырып, ол планетаның орбита бойымен қозғалу жылдамдығы өзгеретінін анықтады, бірақ планетаның радиус-векторы белгілі бір уақыт аралығында тең аудандарды сипаттайды. Кейіннен бұл үлгі Кеплердің екінші заңы деп аталды.
Көбінесе аудан заңы деп аталатын бұл заң 3.6-суретте көрсетілген. Радиус-Вектор бұл жағдайда күнді және планета орналасқан орбитаның нүктесін байланыстыратын айнымалы сегмент деп аталады. AA1, BB1 және CC1 -- планета белгілі бір уақыт аралығында өтетін доғалар. Көлеңкеленген фигуралардың аудандары бір-біріне тең.

Энергияның сақталу заңына сәйкес, тартылыс күштері әсер ететін денелердің жабық жүйесінің толық механикалық энергиясы осы жүйенің денелерінің кез-келген қозғалысында өзгеріссіз қалады. Сондықтан Күнді айналып өтетін планетаның кинетикалық және потенциалдық энергияларының қосындысы орбитаның барлық нүктелерінде өзгермейді және толық энергияға тең. Планета Күнге жақындаған сайын оның жылдамдығы артады-кинетикалық энергия артады, бірақ күнге дейінгі қашықтықтың азаюына байланысты потенциалдық энергия азаяды.
Планеталардың қозғалу жылдамдығының өзгеру заңдылығын анықтай отырып, Кеплер олардың Күнді айналып өтетін қисық сызығын анықтауға кірісті. Ол екі ықтимал шешімнің бірін таңдау қажеттілігіне қойылды: 1) Марс орбитасы шеңбер деп есептеңіз және орбитаның кейбір учаскелерінде планетаның есептелген координаттары бақылаулардан (бақылау қателіктеріне байланысты) 8ʹ-ға алшақтайды деп есептеңіз; 2) бақылауларда мұндай қателіктер жоқ деп есептеңіз, бірақ орбита шеңбер емес. Тихо Брахенің бақылауларының дәлдігіне сенімді бола отырып, Кеплер екінші шешімді таңдап, Марстың орбитадағы позициялары эллипс деп аталатын қисыққа сәйкес келетінін анықтады, ал Күн эллипстің ортасында орналаспайды. Нәтижесінде Кеплердің бірінші заңы деп аталатын заң тұжырымдалды.
Әрбір планета Күнді эллипс бойымен айналдырады, оның бір фокусында Күн орналасқан.
Өздеріңіз білетіндей, эллипс кез-келген P нүктесінен оның фокусына дейінгі қашықтықтың қосындысы тұрақты болатын қисық деп аталады. 3.6 және 3.7 суреттерде: o -- эллипс орталығы; S және S1 -- эллипс фокустары; AB -- оның үлкен осі. Әдетте жартылай үлкен ось деп аталатын бұл шаманың (a) жартысы планетаның орбиталық өлшемін сипаттайды. Күнге ең жақын А нүктесі перигелий деп аталады, ал одан ең алыс В нүктесі -- афелий. Эллипстің шеңберден айырмашылығы оның эксцентриситетінің шамасымен сипатталады: e = OSOA. Эксцентриситет 0 болған жағдайда, фокустар мен центр бір нүктеге біріктіріледі де эллипс шеңберге айналады.
Бір қызығы, 1609 жылы Кеплер өзі ашқан алғашқы екі заңды жариялаған кітап " Жаңа астрономия немесе Марс планетасының қозғалысын зерттеуде көрсетілген аспан физикасы....
1609 жылы жарияланған бұл екі заң да Кеплерді қанағаттандырмай, әр планетаның жеке қозғалысының сипатын ашады. Ол барлық планеталардың қозғалысында "үйлесімділікті" іздеуді жалғастырды және 10 жылдан кейін Кеплердің үшінші Заңын тұжырымдай алды.
Планеталардың айналуының жұлдызды кезеңдерінің квадраттары олардың орбиталарының жартылай үлкен осьтерінің текшелері ретінде өзара байланысты.
Кеплердің үшінші Заңын білдіретін Формула:
T12T22=a13a23,
мұндағы T1 және T2-екі планетаның орбиталық кезеңдері; a1 және a2-олардың орбиталарының үлкен жартылай осьтері.
Кеплер осы Заң ашылғаннан кейін былай деп жазды: "мен 16 жыл бұрын іздеуді шештім, ... ақыры табылды және бұл жаңалық менің барлық күткенімнен асып түсті...
Шынында да, үшінші заң ең жоғары бағалауға лайық. Өйткені, бұл планеталардың күннен салыстырмалы арақашықтықтарын олардың Күнді айналып өтуінің белгілі кезеңдерін қолдана отырып есептеуге мүмкіндік береді. Олардың әрқайсысының күннен қашықтығын анықтаудың қажеті жоқ, кем дегенде бір планетаның күннен қашықтығын өлшеу жеткілікті. Жер орбитасының жартылай үлкен осінің шамасы -- астрономиялық бірлік (А.Е.) -- Күн жүйесіндегі барлық басқа қашықтықтарды есептеу үшін негіз болды.

II. КОСМОЛОГИЯ ЖӘНЕ КОСМОГОНИЯ НЕГІЗДЕРІ

2.1. Жұлдыздар әлемі

Жұлдыз деп қойнауындағы термоядролық ситездік реакциялардың нәтижесінде жылу мен жарықты шығаратын шар тәріздес массивті плазмалық құрылымды айтады.
Жұлдыздар температурасы, түсі және спектрлік класы арқылы ажыратылады (сурет 6).

Сурет 6. Жұлдыздар кластары

Жұлдыздың спектірлік кластарырның реті (сонымен бірге түсі де) латын алфавитінің үлкен әріптерімен белгіленеді: O, B, A, F, G, K, M. Әрбір спектірлік класқа жататын жұлдыздар өз арасында тағы да бөлінеді: 0-ден (ең ыстық) 9-ға (ең суық) болып, мысалы, Күн G 2 спектрлік класқа жатады. Төмендегі 1-кестеде мысал ретінде әр класс жұлдыздарының түсі, температурасы және орналасқан шоқжұлдызы келтірілген.

1-кесте
Жұлдыздарды классификациялаудың кейбір мысалдары
Спектірлік класс
Түсі
Температурасы
Мысалы
Шоқжұлдызы
O
Көгілдір
30 000 К
Беллатрикс
Орион
B
Ақшыл көгілдір
20 000 К
Регул
Арыстан
A
Ақ
10 000 К
Сириус
Үлкен Төбет
F
Ақ сары
8 000 К
Альтаир
Бүркіт
G
Сары
6 000 К
Күн
-
K
Сарғыш
5 000 К
Альдебаран
Торпақ
M
Қызыл
3 500 К
Бетельгейзе
Орион

Салқынырақ жұлдыздардың спектрлерінде молекулаларды жұту жолақтары, ал температурасы жоғарырақ жұлдыздарда бейтарап атомдары жұту жлақтары кездеседі. Күннің спектрі оның құрамында иондалған металдардың бар екенін айғақтайды (бұл Күннің құрметті ақсақалдық жасқа жеткендігінің бір белгісі юолса керек). Ыстық жұлдыздарда иондалған сутек жолақтарының қарқындылығы, ал ең ыстық жұлдыздарда иондалған гелийдің қарқындылығы арта түседі.
Жұлдыздардың температурасын олардың спектрі арқылы (мысалы, спектрлеріндегі әртүрлі сызықтардың қарқындылығы бойынша немесе үздіксіз спектріндегі энергияның таралуы бойынша, тіпті жұлдыздардың түсі бойынша да) анықтайды. Біздер бақылайтын жұлдыздардың спектрі мен жарығы олардың сыртықы атмосфералары шығаратындықтан, анықталған температура мен химиялық құрамы тек жұлдыздардың атмосферасына ғана қатысты болып табылады. Жұлыздардың қойнауындағы температура күрделі теориялық есептеулер арқылы жүргізіледі және ондаған-жүздеген миллион градусқа жетеді.
Жұлдыздардың жарықтылығы (L) деп жұлдыздың бір секундта шығаратын толық жарық энергиясын айтады.
Жарықтылықты қуат бірлігі ваттпен өрнектеуге болады (сондықтан кейде жарықтылық терминін қуат деген терминмен де ауыстырады): жұлдыздардың көбінесе жарықтылығын Күн жарықтылығымен салыстыра өрнектейді, ол 3,85∙1026 Вт құрайды.
Көрінетін жұлдыздық шамма (m) - бұл жұлдыздан бақылаушы тұрған нүктеге қанша жарық келетінін көрсететін жұлдыздық сипаттама.
Жұлдыздардың көрінетін жылтырауы тек шынайы сәуле шығаруына ғана емес, Жерге дейінгі қашықтыққа да байланысты болады.
Абсолюттік жұлдыздық шама (М) - бізден 10 парсек (пк) қашықтықтағы жұлдыздың көрінетін жұлдыздық шамасы. Абсолюттік жұлдыздық шаманы мына формуламен анықтайды:
M = m + 5 - 5lg r,
мұндағы m - көрінетін жұлдыздық шама, r - парсекпен өлшенетін жұлдыздарға дейінгі қашықтық.
1 парсек (1 пк) 3,086∙1013 км-ге тең; бұл жұлдыздан қарағанда Жер орбитасының орташа радиусы (1``) секундқа тең бұрышпен көрінетін қашықтық.
Күннің абсолюттік жұлдыздық шамасы Мк = + 4,8m мәніне тең, бұл стандартты 10 пк қашықтықтан қарағанда Күннің 5-реттік жұлдыздық шамадағы кішігірім әлсіз жұлдыз екендігін білдіреді. (Күннің көрінетін жұлдыздық шамасы m = -27m).
Күннің жарықтылығы мен қандай да бір жұлдыздық шамаларының арасындағы байланыс төмендегі қатынаспен өрнектеледі:
LLк=2,512мк-м
Күннің жарықтылығын Lк = 1 деп қабылдап және Мк = 4,8m екенін ескеріп, жұлдыздың жарықтылығын анықтауға болады: L= 2,51 24,8-м.
Аса алып жұлдыздардың сәуле шығару қуаты (М= -9m), бұл Күн сәулесі қуатынан 330 мың есе артық, ал солғын жұлдыздардың сәуле шығару қуаты (М= 19m) - 480 мың есе кем.
Қызған дененің сәуле шығару спектрінде толқын ұзындықтарының үлкен аумақтары кездеседі. Бірақ дененің температурасы жоғары болған сайын оның сәуле шығару қарқындылығының ең үлкен шамасы толқынның қысқа ұзындығына сәйкес келеді. Математикалық түрде бұл Виннің ығысу заңымен сипатталады:
λmaxT=b
b≈2,89∙10[-3]м∙К -- Вин тұрақтысы. Күннің сәуле шығару максимумы 480 нм толқын ұзындығына сәйкес келеді (сондықтан оның температурасы 6000 К).
Сәуле шығару қуаты да Стефан-Больцман заңы бойынша температураға тәуелді:
ε=σ∙T4,
мұндағы σ=5,67∙10-8 Вт(м2∙К4) - Стефан-Больцман тұрақтысы. Жұлдыздан келетін тұрақты энергияны өлшеп біле отырып, оның температурасын анықтайды.
Жұлдыздардың радиусы олардың жарықтылығы мен температурасы бойынша есептеледі. Стефан-Больцман заңын қолданып, қандай да бір жұлдыз бен Күн үшін жарықтылықтың формуласын жазуға болады:
L=4PIR2σT4,
L⊙=4PIR⊙2σT⊙2,
Мұндағы L және L⊙; T және T⊙; R және R⊙ - cәйкесінше жұлдыз бен Күннің жарықтылығы, сызықтық өлшемдері, абсолюттік температуралары. L⊙=1 және R⊙=1 деп алып, әрі алдыңғы екі теңдікті бір-біріне бөліп, мына өрнекті аламыз: L=R2T4T⊙4, бұдан жұлдыздың радиусын анықтаймыз:
R=LT⊙T2.

Жұлдыздардың параллакстық ығысуы Жердің Күнді айнала қозғалысын дәлелдейді.
Жұлдыздан Жер орбитасының радиусына перпендикуляр қараған кезде орбитаның a орташа радиусы (a = 1 а.б.) толық көрінетін PI бұрышы (сурет 7) жылдық параллакс деп аталады.

Сурет 7. Жұлдызға дейінгі r қашықтықты анықтау

Жылдық паралаксты жұлдызды аспанның бір орнын жартыжылдықтың басында және ортасында суретке түсіре отырып, 0,01`` дейінгі дәлдікпен анықтайды.
Жұлдыздарға дейінгі қашықтықты анықтағанда қолайлы болуы үшін мына өлшем бірліктер қабылданған:
астрономиялық бірлік - Жерден Күнде дейінгң орташа қашықтық:
1 а.б. = 149,6∙109 м.
Парсек (параллакс, секунд) - Жер орбиткасының орташа радиусы 1`` бұрышпен көрінетін қашықтық.
1 пк = 206 265 а.б. = 3,26 жарық жылы = 3,086∙1013 км.
Жарық жылы - жарықтың бір жыл ішінде өтетін қашықтығы.
1 жарық жылы = 0,3069 пк = 9,46∙1012 км = 63 240 а.б.
Жұлдызға дейінгі r қашықтықты (сурет 8) анықтайық:
r = asinPI;sin1``=1206 265 болғандықатан, өте кішкентай PI`` бұрышы үшін:
r=206 265r`` а.б. =1PI``пк.

Күн жүйесіне жақын жұлдыз Центавр Проксимасына дейінгң қашықтық 4,24 жарық жылына тең (автокөлік бұл қашықтықты тоқтаусыз 100 кмсағ жылдамдықпен 40 млн жылда өтеді).
Аспандағы жұлдыздардың бұрыштық орнын ауыстыруларын меншікті қозғалыстары деп атайды. Меншікті қозғалысты және жұлдыздарға дейінгі қашықтықты біле отырып, тангенциалды жылдамдықты анықтауға болады (сурет 8):
v1=4,74μ``PI``кмс
мұндағы μ - меншікті қозғалыс, яғни аспан сферасында жұлдыздың бір жыл ішінде көрінетін бұрыштық ығысуы; PI - жылдық параллакс.

Сурет 8

∆λ спектрлік сызықтардың ығысуын өлшеп, жұлдыздардың сәулелік жылдамдығын анықтауға болады:
vr=∆λλc.
Жұлдыздың кеңістіктің жылдамдықтарын мына формуламен анықтайды:
v=vr2+vt2
Жұлдыздардың жылдамдықтары секундына ондаған километрді құрайды. Зерттелген жұлдыздардың ішінен жоғары жылдамдыққа Көгершін шоқжұлдызындағы әлсіз жұлдыз ие. Жұлдыздардың кейбірі (мысалы, Гиадтар) өзара тартылысы мен пайда болуының ортақтылығына байланысты бірдей жылдамдықпен параллель қозғалады. Сонымен қатар жұлдыздар Галактика центірі төңірегінде айналады. Әр жұлдыздың меншікті жылдамдығы болады. Күн апекс деп аталатын Геркулес шоқжұлдызы бағытында, аспан сферасының координаталары α=270°; δ=+30` нүктеге қарай, көршілес жұлдыздармен салыстырғанда 19,4 кмс жылдамдықпен қозғалады.
Жұлдыздардың жылдамдықтарының жоғары болуына қарамастан, олардың аспандағы көрінетін орны өте баяу өзгереді. Біздің Жердегі өркениет уақыты ішінде шоқжұлдыздардың бәрі де өз орналасу қалыптарын елеулі өзгерткен жоқ.

2.2. Жұлдыздар эволюциясы

Жұлдыздар заманауи тұжырымдамалар бойынша жұлдызаралық ортадаға заттың гравитациялық сығылуы нәтижесінде түзіледі. Алып (шамамен 100 пк аймақты қамтитын ) кешен сығылады, тығыздалады және әрі қарай сығылуы барысында қоймалжың жиынтықтарға (протожұлдыздарға) ыдырайды. Жиынтықтар әрі қарай сығылуын жалғастырып, температурасы 10 млн градусқа жеткенде термоядролық рекция басталады да, жұлдыз жалын шашып маздайды; сығылу процесі тоқтайды, өйткені гравитациялық сығылу күшіне термоядролық реакцияларда бөлініп шыққан ғаламтор зор сәулелік энергияның қысымы қарсы тұрып, тепе-теңдік орнайды.
Термоядролық реакциялар барысында сутек гелийге айналып энергия бөліп шығарады. Күн өзінің сутек қорын шамамен 10 млрд жылда аяқтайды. Жұлдыздардың өмір сүру ұзақтығының оның массасына тәуелділігін №1 қосымшадағы кестеден көруге болады.
Күннің ядросындағы сутек отыны жануына қарай, оның сыртқы қабықшасы ұлғайып, яядросы сығылып, қыза түседі. Ядро ішіндегі сутек толық жанып біткен соң термоядролық реакциялар ядроның жұқа сыртқы қабатында жалғасады. Күн қазіргі уақыттан бастап әлі 4,6 млрд жыл бойы кеңейіп, қызыл алыпқа айналады (сурет 9). Күннің эволюциясы асқынжаңа жұлдыздардың жарылысы сияқты жарылумен аяқталмайды, өйткені ондай жарылыс үшін оның массасы тым аз болып табылады.

Сурет 9. Алдағы 4,5 - 5 млрд жыл Сурет 10. Асқынжаңа жұлдыздың
ішіндегі Күн эволюциясы 1054 жылғы жарылысы

Күн қызыл алып фазасынан өткеннен кейін оның қабығы ажырап, одан планеталық тұмандық пайда болады. Бұл тұмандықтың центірінде көлемі Жермен шамалас Күн ядросының қалдығы өте тығыз, әрі ыстық ақ ергежейлі пайда болады. Ақ ергежейлі бетінің температурасы 120 000 К, ол көптеген миллион және миллиард жыл бойы суып, өшеді. Мұндай ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.