Жарық толқындарының интерференциясы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 36 бет
Таңдаулыға:

М.Өтемісов атындағы Батыс Қазақстан университеті

Факультет: Физика - математика
Кафедра: Физика
Жоба авторлары: Мақсот Аяулым
Зинекеева Ақторғын
Жубанчалиева Жанна
Бекесов Рахман
Курс: 3
Топ: МФ-33
Пәні: Әлемнің физикалық көрінісі
Ғылыми жетекшісі: Кадырова Г. М.

Жоба тақырыбы:

Жарық идеясының дамуы

Орал, 2022
Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3
І Жарық құбылыстары
1.1Жарық табиғаты ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .4
1.2 Жарықтың қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...17
1.3 Жарықтың таралуы, шағылуы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...19
1.4 Ақ жарықтың спектрге жіктелуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 29
ІІ Практикалық бөлім
2.1 Жарықтың интерференциясы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...32
2.2 Жарықтың сынуы ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 33
2.3 Жарықтың спектрге жіктелуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..34
2.4 Есеп ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...35
2.5 Кестелік мәліметтер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... .36
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..41
Пайдаланылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ...42

Кіріспе

Өзектілігі: Жарық идеясының дамуы жобасы: Жарық - қуаттың бір түріне жатады. Осының арқасында тірі жаратылыстардың барлығы, оның ішінде адам баласы да айналасындағы әлемді көре алады. Жарықтың өзі көзге көрінбейді,алайда өзі басқа заттардың барлығына көруіне себепші болады.
Жобаның мақсаты: Жарық, жарық интерференциясы, дифракциясы, ақ жарықтың спектрге жіктелуі туралы түсінік беру. Практикалық тұрғыдан жарықтың сыну заңын, жарықтың түрлі түсті спектрге жіктелуін, интерференция құбылыстары туралы зерттеу
Зерттеу объектісі: Әр түрлі ортадағы судың сыну көрсеткіші, интерференция құбылысы, жарықтың спектрге бөлінуі
Зерттеу пәні: Әлемнің физикалық көрінісі.
Жобаның міндеттері:
- жарық туралы жалпы түсінік беру;
- кестелік мәліметтерді талдау; жарықтың сыну заңы арқылы есептер шешу;
- ақпараттық және жазбаша біліктілікті арттыру;
- жоба презентациясын даярлау;
- жарық құбылыстары туралы ақпаратты жетік меңгеріп,терең қалыптастыру.
Маңыздылығы:
− Студенттер мен қатысушылардың оқу үрдісіне талқыланған материалдарды пайдалану мүмкіндігі.
Орындаушылар үшін:
− зерттеу нысаны мен пән туралы білімдерін кеңейту және толықтыру.

І Жарық құбылыстары
1.1 Жарықтың табиғаты
Оптика - физика ғылымының дербес салаларының бірі. Оптикада жарық пен рентген сәулелерінің табиғаты мен қасиеттері және олардың затқа ететін әсерлері қарастырылады.[1]
XVII ғасырдың аяқ кезінде жарықтың табиғаты жайында екі түрлі ғылыми түсінік болды. Олардың біреуі - жарықтың корпускулалық теориясы, екіншісі - жарықтың толқындық теориясы.
Жарықтың корпускулалық теориясын тұжырымды етіп баяндаған - ағылшынның атақты ғалымы И.Ньютон (1672 ж.). Бұл теория бойынша, жарық дегеніміз -- жарқырауық денелерден ұшып шыққан жарық бөлшектерінің (корпускулалардың) ағыны. Ньютонның ойынша, жарық бөлшектері инерция заңына лайық түзу сызық бойымен қозғалады, сондықтан жарық біртекті ортада тузудің бойымен таралады. Екі мөлдір ортаның шекарасында жарықтың сыну себебі жарық бөлшектері сындырушы ортаның бөлшектеріне тартылады, соның салдарынан бірінші ортадан екінші ортаға өткенде жарық бөлшектерінің жылдамдығы өзгереді, сонда бірінші ортадан гөрі екінші орта тығыздау болса, жарық бөлшектеріңің жылдамдығы артады.[6]
Интерференция құбылысын толқынның интерференциясын мысалға ала отырып түсіндіруге болады. Жарық интерференциясы үшін қажетті шарт: жарық толқындары монохроматты және когерентті болуы қажет. Интерференция құбылысын бақылау үшін, бір жарық көзінің сәулесін екі саңылаудан өткізіп, оларды когерентті жарық көздері ретінде қарастырады.
(1)
мұнда - толқындар жүрісінің айырмасы; ; - экран ортасынан интерференция бақыланатын А нүктесіне дейінгі қашықтық.
Толқындар жүрісінің айырмасы , болғанда интерференциялық максимум, ал , болғанда интерференциялық минимум бақыланады.
Бақыланылатын нүктедегі максимум
; (2)
ал минимум
; (3)
Көршілес екі максимумдар (немесе) минимумдардың арақашықтығы интерференциялық жолақтың ені делінеді.
(4)
Табиғатта жұқа қабықшаның екі жазықтығынан шағылған жарық интерференция нәтижесінде қабықшаның түрлі түске боялынуын бақылауға болады.
Қалыңдығы мөлдір пластинаға сәуле бұрышпен түссін. нүктесінде сәуленің біразы шағылып 1 сәуле түрінде ауаға өтеді. Сынған сәуле С нүктесінде біразы шағылып В нүктесіне келеді. Бұл нүктеде біразы шағылып, біразы сынып 2-ші сәуле түрінде ауаға өтеді.
d

i
0
r
C
A
B
i
P
1
2
d

i
0
r
C
A
B
i
P
1
2

1.1-сурет. Жұқа қабықшадағы интерференция

Пластинаның жоғарғы және төменгі беттерінен шыққан 1 және 2 сәулелер когерентті. Егер бұл сәулелердің жолына жинағыш линза қойса линзаның фокальдық жазықтығында (Р нүктесінде) интерференциялық бейнені бақылауға болады. Интерференцияланушы бұл сәулелердің жазықтығына дейінгі жүрген оптикалық жол ұзындықтарының айырмасы
(5)
Оптикалық жол ұзындығы геометриялық жол ұзындығы мен ортаның сыну көрсеткішінің көбейтіндісіне тең. Пластинаның сыну көрсеткіші 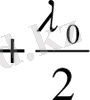, пластинаны қоршаған ауаның сыну көрсеткіші мүшесі жарықтың орталар шекарасында шағылу нәтижесінде жоғалатын толқын шамасы. Егер () болса, жарық толқынның жоғалуы нүктесінде болады, онда, таңбасы теріс (), ал болса, жарық толқын жоғалуы С нүктесінде болады да, таңбасы плюс болады.
; және олай болса
(6)
Р нүктесінде максимум болады, егер
, (7)
минимум болады, егер

, (8)
Интерференция құбылысы дәлді өлшеуіш приборларда - интерферометрлерде қолданылады.

Жарық толқындарының интерференциясы
Белгілі бір жағдайда екі (немесе бірнеше) толқынды қозғалыстардың қабаттасу құбылысы интерференция деп аталады. Құбырдағы екі дыбысты толқынның интерференциясын қарастырайық. Бір жылжулар толқыны x өсінің оң бағытымен таралады және былайша анықталсын делік:
, ал екіншісі
біріншісіне қарсы таралады. Екінші y2 толқынды қашанда екі қума толқынның қосындысы деп қарастыруға болады, атап айтқанда:
(9)
Онда y(x, t) қорытқы толқындық қозғалыс екі бөлімнен тұрады: тұрғын толқыннан
және қума толқыннан.
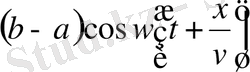b=a болғанда, яғни бір біріне қарама-қарсы бағыттағы екі жүгірме толқындардың амплитудалары бірдей болған кезде қорытқы толқындық қозғалыс тұрғын толқын пайда болады.
Жылжымайтын нүктелер тұрғын толқынының түйіндері, ал ығысуы барынша үлкен нүктелер тұрғын толқынының шоқтары деп аталады.
Фазалық жылдамдық. Синусоидалық толқынның v таралу жылдамдығы фазалық жылдамдық деп аталады. Ол синусоидалды толқын фазасының кез келген кесімді мәніне сәйкес келетін кеңістікте орын ауыстырған бет нүктелерінің жылдамдығына тең. Мысалы, жазық синусоидалды толқынға байланысты шартынан шығатыны:
, мұнда k - толқындық сан: .
Бейгармоникалық толқынның (толқындық пакеттің) таралу жылдамдығы ретінде толқын амплитудасы максимумының орын ауыстыру жылдамдығын алады. Максимум толқындық пакеттің центрі ретінде қарастырылады. tdw-xdk=const шарты ретінде орындалса, онда:
dxdt=dwdk=u (10)
Мұндағы u топтық жылдамдық. Оның фазалық жылдамдықпен (υ=wk) байланысы мынадай: u=υ-λd υdλ.
Когеренттілік деп кеңістікте және уақыт бойынша бірнеше тербелістің немесе толқындық жүйелердің үйлесімді түрде өтуін айтады.
Монохроматты толқындар - бір ғана тұрақты жиіліктегі бүкіл кеңістік бойынша шектелмей таралған толқындар. Нақтылы жарық көздері аса дәл монохроматты жарық бермейтіндіктен кез келген бір бірінен тәуелсіз жарық көздерінен шыққан сәулелер когерентті болмайды. Жарықты жарық көздеріндегі әрбір атомдар шамамен 10-8c. уақыт мезетінде шығарады. Тек осы сәтте ғана атомдар шығарған толқындардың амплитудасы және тербеліс фазасы тұрақты болады. Монохроматты емес жарықты толқындық түйіншектер (волновые цуги) - атомдар шығаратын, бірін-бірі тез алмастырып тұратын гармониялық импульстердің жиыны түрінде қарастыруға болады.
Бір толқындық түйіншектің орташа уақыты когеренттілік уақыты деп аталады. Егер толқын біртекті ортада таралса, онда тербеліс фазасы кеңістіктің берілген нүктесінде тек когеренттілік уақытында ғана сақталады. Бұл уақыт мезетінде толқын вакуумде lког = с τког ара қашықтығына тарайды. Бұл ара қашықтықты когеренттілік ұзындығы (немесе түйіншек ұзындығы) деп атайды. Сондықтан берілген жарық көзі үшін интерференцияны тек оптикалық жол ұзындығы когеренттілік ұзындығынан аз болғанда ғана бақылау мүмкін.
Уақытша когеренттілік деп -- толқынның монохроматтық дәрежесімен анықталатын кеңістіктің берілген нүктесіндегі тербеліс когеренттілігін айтады. Уақытша когеренттілік берілген нүктедегі фазалардың өзгешелігі мәніне жеткенше сақталады.
Когеренттілік ұзындығы деп -- толқынның когеренттілік уақытындағы ығысатын ара қашықтығын айтады.
Толқын түйіршігінің таралу бағытына перпендикуляр жазықтықта екі нүктенің ара қашықтығы артқанда олардың фазаларының кездейсоқ өзгеруі де артады.
Кеңістіктік когеренттілік - уақыттың бір мезетіндегі кеңістіктің әртүрлі нүктелеріндегі когеренттілік.
Кеңістіктік когеренттіліктің ұзындығы (когеренттілік радиусы): , мұндағы λ - толқын ұзындығы, Δφ- фазалар айырымы.
Жарық толқындарының интерференциясы байқалу үшін жарық көздері кеңістіктік когерентті болуы тиіс.
Жарық интерференциясы деп -- кеңістікте екі немесе одан да көп когерентті жарық толқындарының беттесуінің нәтижесінде қорытқы толқынның амплитудасының күшейуін немесе әлсіреуін айтады.
Интерференциялық максимум шарты: Егер оптикалық жол айырымы вакуумдағы толқын ұзындығының бүтін санына (жарты толқын ұзындығының жұп санына), яғни
болса, онда болып, тербеліс бірдей фазада болады.
Интерференциялық минимум шарты: Егер оптикалық жол айырымы Δ, жарты толқын ұзындығының тақ санына , яғни
болса, онда болып, тербеліс қарсы фазада болады.
Интерференцияны байқаудың әдістері.
Лазер ойлап табылғанға дейін когерентті жарық шоқтарын екіге бөліп, әртүрлі оптикалық жол жүрген соң қайта беттестіріп, интерференциялық суретті байқаған.
1. Юнг әдісі. Өте жарықтанған S саңлауынан жарық екі S1 және S2, саңлауларына түсіп, ВС интерференция экранда байқалады (1.2-сурет).

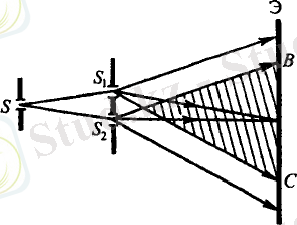
1.2-сурет. Юнг әдісі

2. Френель айнасы. Жарық S көзінен бір-біріне өте аз φ бұрышпен орналасқан екі жазық А1О және А2О айналарына түседі. Когерентті жарық көздері ретінде S1 және S2 жорамал көздері алынады.

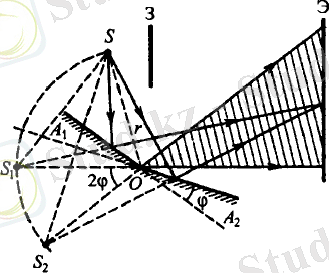
1.3-сурет. Френель айналары

Интерференциялық сурет жарықтың тікелей түсуінен қалқаланған Э экранында байқалады (1.3-сурет).
3. Френельдің қоспризмасы. S көзінен шыққан жарық призмалардан сынады да қоспризманың сыртында екі жорамал S1 және S2 жарық көздерінен тарағандай болады.

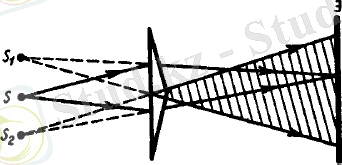
1.4-сурет. Френельдің қоспризмасы

4. Ллойд айнасы. S жарық көзі М жазық айнасына өте жақын орналасады. Бұл жағдайда S жарық көзі мен оның айнадағы жорамал S1 бейнесі когерентті жарық көздері болып табылады.

1.5-сурет. Френель айнасы

Екі саңлаудан байқалатын интерференциялық суретке есептеулер жүргізу.
Екі S1 және S2 саңлаулары бір-бірінен d ара қашықтықта орналасқан және когерентті көздер болсын. Э экраны саңлауларға параллель және одан ld ара қашықтықта орналассын (1.5-сурет).

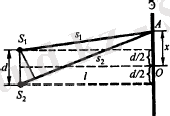
1.6-сурет. Екі жарық көзінен шыққан жарық толқындарының
интерференциясы

Кез-келген A нүктесіндегі жарық қарқындылығы мына жол айырымымен анықталады:
= S2 - S1 ,
мұндағы ,
,
бұдан немесе , l d болғандықтан , сондықтан
Максимумдардың орны
Минимумдардың орны:
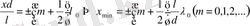
Екі көрші максимумдардың (минимумдардың) x ара қашықтығы интерференциялық жолақтың ені деп аталады.
(11)
Интерференциялық сурет бір-біріне параллель әрі бірін-бірі кезек алмастыратын жарқын және солғын жолақтар түрінде байқалады.
Жұқа қабыршықтағы жарық интерференциясы
Мұнайдың жұқа қабыршығымен қапталған су бетінде, сабын қабыршығының бетінде және т.б. бақыланатын жұқа қабыршықтардың кемпірқосақ тәрізді түсі жұқа қабыршықтағы интерференциямен түсіндіріледі (9-сурет).

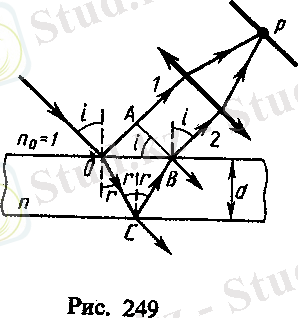
1.7-сурет. Жазық параллель пластинадағы интерференция

Параллель сәулелер шоғы қалыңдығы d мөлдір қабыршық бетке i бұрышымен түскенде, жарық бұл беттен жартылай шағылып, жартылай қабыршық арқылы өтіп, екінші беттен шағылады, қабыршық арқылы қайта өтедіде қабыршықтан шығып бірінші беттен шағылған жарықпен кездеседі. Бұл сәулелердің жүріс жол айырымы суреттен мынаған тең екендігін байқаймыз: 2dn cosr. Мұндағы n қабыршықтың сыну коэффициенті. Өйткені
Қабыршықты қоршаған ортаның сыну көрсеткіші n=1-ге тең деп алынған, ал 2 жарықтың бөлік шекарасында шағылуымен байланысты жарты толқын ұзындығын жоғалтуынан. Егер nn болса, онда жарты толқын О нүктесінде жоғалады да жоғарыда аталған мүше таңбасы минус болады; егер nn болса, онда жарты толқын С нүктесінде жоғалады. Онда, 2 таңбасы плюс болады. Жарықтың сыну заңын ескерсек (sin i=nsinr), онда nnүшін мынаны аламыз:
+2 (12)
Жұқа қабыршақтағы интерференциялық максимум шарты мынандай:
2d+ 2=m (m=0,1,2,...)
Ал минимум шарты мынадай:
2d+ 2= (2m+1) 2 (m=0,1,2,...) (m=0,1,2,...)
1. Тең көлбеулік жолақтар (жазық параллель пластинкадағы алынған интерференция) Берілген , d және n үшін сәулелердің әрбір i көлбеулігіне интерференциялық жолағы сәйкес келеді. Жазық параллель пластинкаға бірдей бұрыштармен түскен сәулелердің қосылуынан пайда болған интерференциялық жолақтар тең көлбеулік жолақтар деп аталады.
2. Тең қалыңдықты жолақтар (қалыңдығы айнымалы платинкадан алынған интерференция). Егер қабыршықты экранға экранда қабыршық кескіні алынатындай етіп линза арқылы проекцияласа, онда қабыршықтың тең қалыңдықтарына сәйкес нүктелер бойынша өтетін жолақтармен жабылады.

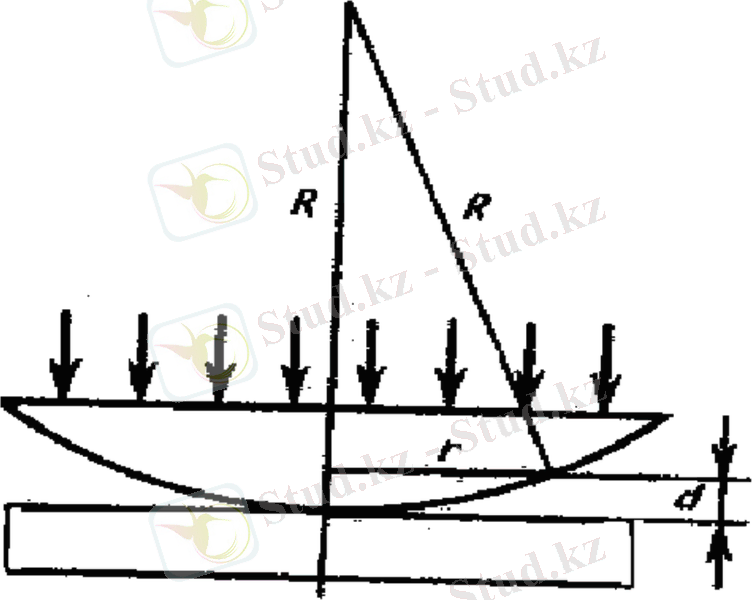
1.8-сурет. Ньютон сақиналары

1. Тең қалыңдықты жолақтардың классикалық мысалына Ньютон сақиналары жатады. Бұл сақиналар жарықтың жазық параллель пластинкамен оған жанасқан қисықтық радиусы үлкен жазық дөңес линзаның арасындағы ауа саңлауында бақыланады. Жарықтың параллель шоғы линзаның жазық бетіне тік түседі де, линза мен пластинка арасындағы ауа қабатының жоғарғы және төменгі беттерінен жартылай шағылады. Шағылған сәулелер қосылғанда тең қалыңдықты жолақтар пайда болады. Жарық тік түскенде ол жолақтардың пішіні концентрлі шеңбер болады.
Шағылған жарықта оптикалық жүріс жол айырымы мынаған тең болады (n=1 ауа үшін және i=0) , d - саңлау ені. Суреттен d - ның аз екендігін ескеріп мынаны аламыз:
(13)
Онда интерференциялық максимум және минимум шарттарына сәйкес m - ші жарық және сәйкес m - ші қараңғы сақиналар. Радиустері тиісінше мынадай болады:
(m=0, 1, 2, ...), (m=1, 2, 3, ...)
Қазіргі обьективтерде пайдаланылатын линзалар саны өте көп болғандықтан, олардан шағылу да көп. Сондықтан жарық ағынының шығыны да үлкен болып келеді. Өткен жарықтың интенсивтігі әлсірейді, оптикалық аспаптың жарық күші кемиді. Бұл кемшілікті болдырмас үшін оптиканың жарықталынуын жүзеге асырады. Ол үшін линзаның бос бетіне сыну көрсеткіші линза материалының сыну көрсеткішінен аз жұқа қабатымен қаптайды.
Жарық ауа - қабыршық және қабыршық - шыны аралықтарының шекараларында шағылған кезде және когерентті сәулелердің интерференциясы пайда болады (9-сурет).

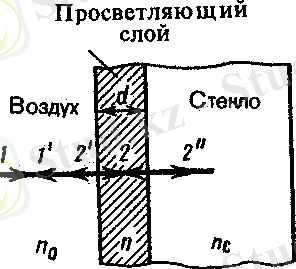
1.9-сурет. Оптиканың жарықталынуы

Қабыршықтың қалыңдығы мен шынының және қабыршықтың сыну көрсеткіштерін (n) және (n)қабыршықтың екі жақ бетінен шағылған сәулелер бірін-бірі өшіретіндей етіліп таңдалып алынады. Сонда мына шарттар орындалуы тиіс:
және nd=4

Жарық толқындарының дифракциясы
Гюйгенс - Френель принципі.
Дифракция - жарық толқындарының жолдарында кездескен бөгеттерді орағытып өтуі, немесе, анығырақ айтқанда -- толқындардың таралу кезіндегі кез-келген бөгеттерден, яғни, геометриялық заңдылықтардан ауытқуы.
Дифракцияның негізгі заңдылықтары екі принцип арқылы түсіндірледі:
1. Гюйгенс принципі. Уақыттың кез-келген мезетінде жарық толқыны тарайтын толқындық беттің әр бір нүктесін элементар толқын көзі деп қарастыруға болады.
2. Интерференция заңы. Жарық толқын бетінің барлық нүктесі бірдей жиілікте тербеліп тұрады. Олардың фазалары да бірдей. Олай болса, оларды когерентті жарық көзінің жиынтығы деп қарастыруға болады.
Френель осы екі принципті біріктірді. Ол Гюйгенс - Френель принципі деп аталады. Бұл принцип бойынша толқын бетінің фронтының алдыңғы жағындағы нүктедегі тербелісті табу үшін сол нүктедегі толқындық беттің барлық нүктелерінен келген тербелістерді тауып, одан кейін олардың фазалары мен амплитудаларын ескере отырып қосу керек.

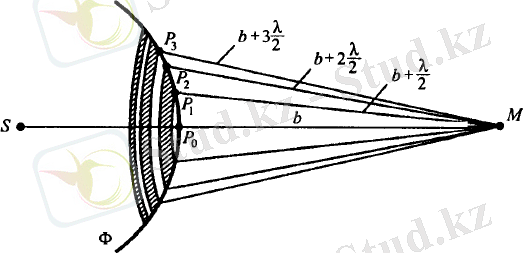
1.10-сурет. Френель зоналары

Френель зоналары. Гюйгенс принципі түсіндіре алмайтын жарықтың түзу сызық бойымен таралу заңын Гюйгенс-Френель принципі бойынша түсіндіруге болады. S жарық көзінен жарық толқыны таралсын. Гюйгенс принципі бойынша жан-жаққа сфералық жарық таралады. Радиусы Р сфералық бет Φ жүргізейік. Енді M нүктесіндегі жарық толқынының әсерін анықтау үшін сол толқындық бетті дөңгелек зоналарға бөлеміз. Көршілес сфералар радиустарының бір-бірінен айырмасы λ2 - тең болатындай етіп аламыз. Сонда 1-ші сфераның радиусы b1=b0+λ2, 2-кі b2=b1+λ2, тағы сол сияқты - bm=bm-1+λ2. Осы сфералар Φ толқындық бетті бірнеше зонаға бөледі. Оны Френель зоналары деп атайды.
М нүктесіне келген тербелістер амплитудасы кішірейе береді (A1A2A3... Аm),. Мұндағы A1 - орталық зонадан, A2, A3, A4...-1,2, зоналардан келген толқындар қоздырған тербелістердің амплитудалары. М нүктесіне көршілес екі зонадан келетін тербелістердің фазалары қарама-қарсы болатындықтан, m зоналар әсерінен пайда болған қорытқы тербелістің А амплитудасы мынаған тең болады: А=А1-А2+А3-А4+...Аm. Егер m 1, A1Am болған жағдайда :
(14)
Сөйтіп, өте көп зоналар немесе өте үлкен толқындық бет әсерінен пайда болған қорытқы тербелістің амплитудасы, орталық зонаның әсерінен пайда болған тербеліс амплитудасының жартысына тең. Барлық Френель зоналардың бетінің ауданы тең. Сыртқы Френель зонасының радиусы тең.
Сонымен, жарықтың бір текті ортада түзу сызықтың бойымен таралуы элементар толқындар интерференциясының нәтижесі болады.
Френель дифракциясы. Егер жарық дифракцияланатын бөгет жарық көзімен бақылау нүктесіне жақын болса, сондағы байқалатын жарық дифракциясы Френель дифракциясы деп аталады. Дифракцияның бұл түрі кейде тоғысатын сәулелер дифракциясы деп те аталады.
Жарықтың кішкене дөңгелек саңылаудан өткенде дифракциялануы. Жарқырауық S нүктеден таралған жарық жолына экран қояйық, оның кішкене дөңгелек саңлауы болсын. Саңлауға сиятын зоналар саны саңлаудың өлшемдеріне байланысты. Егер саңлаудың ауданына сыйған зоналар саны тақ және шақтаулы болса, онда B нүктесінің жарықталынуы максималь болады. Ал енді аумақтан жарық көзі мен бақылау нүктесіне дейінгі аралықтар тұрақты болған жағдайда аумақты жайлап үлкейтсе, онда одан өтетін зоналар саны көбейеді, олардың саны тақ болғанда B нүктесінің жарықталынуы күшейеді, жұп болғанда - нашарлайды.

1.11-сурет. Френель дифракциясы

Жарықтың кішкене дөңгелек экран шетінен дифракциялануы. Жарқырауық S нүктеден таралған сфералық жарық толқынның жолында кішкене дөңгелек Э экран тұрған болсын. Сонда ол экран толқындық беттің орталық бөлігін бөгелтеді.
Егер дөңгелек Эm Френель зоналарды жапса, онда экранда тербелістің амплитудасы:

Сонымен B нүктесінде әрқашан интерференциялық максимум байқалады.
Параллель сәулелердің дифракциясы (Фраунгофер дифракциясы). Егер бөгет жарық көзінен өте алыс болса, онда сол бөгетке түсетін жарық шоғы параллель болады, өйткені шексіз қашық толқындық бетті жазық бет деп санауға болады. Егер осындай жазық жарық толқыны дифракцияланғаннан соң жарық сәулелері бұрынғыша параллель болып таралса, сондағы байқалатын жарық дифракциясы Фраунгофер дифракциясы, немесе параллель сәулелер дифракциясы деп аталады.
Ені a=MN ұзын саңлауда болатын Фраунгофер дифракциясын қарастырайық. MC және ND шоқтарының арасындағы жүру жолдарының оптикалық айырмашылығы:
∆= NF sin aφ.MN толқындық бетті Френель зоналарына бөлейік. Әр зонаның еніне ∆:λ2 зона сәйкес келеді. Толқындық фронттың әр нүктесінің фазасы және амплитудасы біркелкі. Сондықтан көршілес Френель зоналарының тербеліс қарқындылығы нольге тең болады. Яғни:
1)егер, Френель зоналарының саны тақ болса,онда: дифракциялық минимум шарты
2)егер, Френель зоналарының саны жұп болса, онда
дифракциялық максимум шарты
Дифракциялық тордағы Фраунгофер дифракциясы.
Бір саңылаудан пайда болатын дифракцияны қарастырғанда ақ және қараңғы жолақтар бірінен кейін бірі орналасқанын байқадық.

1.12-сурет. Бір саңылаудағы Фраунгофердің дифракциясы

Енді жарық сәулелерін бір саңылаудан ғана өткізбей, осындай бірнеше саңылаудан өткізсек, онда пайда болған ақ және қара жолақтардың ені бір саңылаудан өткен жолақтардың еніне қарағанда енсіздеу (аздау) және жарығырақ болатыны байқалған. Осы жолақтарды дифракциялық бейне деп атайды. Ондай бейнелерді алу үшін дифракциялық тор пайдаланылады. Дифракциялық тор деп параллель орналасқан ені бірдей саңылаулар жиынтығын айтамыз. Дифракциялық тор әдетте шыны пластинканың бетіне сызат жасау арқылы алынады. 1мм шыны пластинкаға 1200-ге дейін сызат салынады. Егер жарық өткізбейтін бөліктің енін b, ал өткізетін бөліктің енін a десек, онда d=a+b - тор периоды деп аталады. Тор периоды мен жарықтың толқын ұзындығының арасында мынадай байланыс бар: , мұндағы к=0, +-1, +-2...- спектр реті.
Дифракциялық тор күрделі жарықты спектрлерге жіктей алады. Сондықтан дифракциялық тор жарық құрамын зерттеу үшін пайдаланылатын құралдардың негізгі бөлігі болып саналады. Ол құралдарды торлы спектрлік құралдар немесе дифракциялық спектроскоп деп атайды.
Дифракциялық тордың ажырату қабілеті деп толқын ұзындықтарының айырмасы өте аз, екі сызықты спектрді ажыратып бақылау мүмкіншілігін айтады. Тордың ажырату қабілетін сан жағынан сипаттау ретінде мынадай шама қабылданған:
(15)
Бұл шаманы басқаша дифракциялық тордың ажырату күші деп атайды. Мұндағы λ - ажыратылатын сызықтық спектрлердің толқын ұзындықтарының орташа мәні; - олардың толқын ұзындықтарының айырымы, яғни бір бірінен ажыратуға болатын толқын ұзындығының мәні.
Теория жүзінде дифракциялық тордың ажырату қабілеті тор саңылауларының жалпы санына N пропорционал болатындығын дәлелдеп көрсетуге болады. Яғни:
A=Kn (16)

мұндағы: k-спектрдің реттік саны. Сонымен тордың ажырату қабілеті оның саңылауларының жалпы саны мен спектрдің қайталану қатарын көрсететін реттік санның көбейтіндісіне тең шама болады.
Егер параллель рентген сәулелерінің шоғы атомдық жазықтыққа бұрышпен кристаллға түссе, және сәулелер кристалдың атомдық жазықтықтарының бір қатарынан шағылса, онда кристалдың көршілес атомдарының (немесе иондарының) қабаттарынан шағылған сәулелер арасында жүріс жол айырымы пайда болады. Мұндағы d - кристалдағы атомдар (немесе иондар) қабаттарының арасындағы ара қашықтық.
Дифракцияланатын сәулелер интенсивтігінің максимумы жүріс жол айырымы толқын ұзындығының бүтін санына тең болатын бұрышқа сәйкес келеді:
(к=0,1,2,3,) (17)

Бұл формула Вульф-Брэгг формуласы деп аталады. [14]

1.2 Жарықтың қасиеттері
Жарық және жарық құбылыстары туралы ілімді физиканың оптика деп аталатын бөлімі қарастырады. Негізгі оптикалық құбылыстарды білудің үлкен танымдық және практикалық мәні бар. Біз әр түрлі жарық құбылыстары бар дүниеде өмір сүреміз. Олардың пайда болу себептерінен хабарсыз жандарға көптеген жарық құбылыстары таңғаларлық және құпия болып көрінеді. Егер біз олар жайлы ғылыми түсінік алсақ, олардың басқа құбылыстармен байланысын тапсақ және оларды табиғаттың белгілі заңдары негізінде түсіндірсек, онда бұл құбылыстардың құпиясын аша аламыз. Бұл жобада біз жалпы түрде әр түрлі жарық көздерімен, жарықтың таралу заңдарымен, оның денеге әсер етуімен және оптикалық аспаптармен танысамыз.[2]
Біздің планетамыздағы өсімдіктер мен жануарлар әлемінің тіршілігі үшін жарықтың алатын орны ерекше.
Жарық табиғатты танудағы маңызды құрал болып табылады. Қоршаған дүниені көреміз, ал көру мүшесі көз деп аталады. Бізді қоршаған дүние туралы мәліметтің 90%-ын біздің көру мүшеміз береді, ал оның тасымалдаушысы жарық болып табылады. Жарық біз көреміз бе, әлде жоқ па, оған тәуелсіз өмір сүреді, өйткені жарық көздері біздің санамызға тәуелді емес.
Аспан денелерінен келетін жарықтың көмегімен Күннің, Айдың, жұлдыздардың, планеталардың және т.б. орналасуы мен қозғалысы анықталған. Жарық құбылыстарының зерттелуі, көптеген физикалық, астрономиялық, химиялық, биологиялық құбылыстарды зерттеп ашуға септігін тигізген әр түрлі оптикалық аспаптарды жасауға мүмкіндік берді. Жарық тұрмыста, медицинада, қозғалыс қауіпсіздігі үшін әскери техникада қолданылады.
Жарық нені білдіреді?
Жарық ағынында молекулалар да, атомдар да, электр бөлшектері де, заттың кандай да бір басқа бөлшектері де жоқ.
Жарық - - заттың бөлшектерінің табиғатынан бөлек, табиғаты ерекше бөлшектер ағыны болып табылады. Жарық бөлшектері фотондар деп аталады.
Фотондар ағыны энергияны жарық көздерінен жарықталынған денелерге жеткізеді. Бұл энергияны жарық энергиясы немесе жарықтың сәуле шығару энергиясы деп атайды. Бұл туралы толығырақ жоғары сыныптардан таныспыз. "Сәуле шығару" деп аталатын энергияның берілу түрі бар екенін біз бұрыннан білеміз.
Сәуле шығару толық вакуумде болуы мүмкін. Барлық денелер өздерінің ішкі энергиясын азды-көпті сәулелену арқылы шығарады.
Түсетін сәулелену энергиясын денелер жартылай жұтады, соның нәтижесінде денелер қызады.

Осы сәулеленудің барлық ерекшеліктері жарыққа да тән. Жарық дегеніміз -ол да сәулелену, бірақ оны көзбен қабылдайтын болған соң, жарықты көрінетін сәулелену деп те атайды.
Жарық немесе фотондар ағыны денелерге түсіп, заттың бөлшектерімен өзара әсерлеседі. Жарық әсерінен денелер қызады, металдардан электрондар ұшып шығады, осының нәтижесінде металдар электрленеді. Жарық әр түрлі химиялық реакциялар тудырады, мысалы, маталарда бояудың оңуы, фотопластинкалар мен фотопленкалардың қараюы. Өсімдік жапырақтарында жарық әсерінен хлорофилл түзіледі. Шебер жасалған тәжірибелердің көмегімен жарықтың денелерге түсіретін қысымын, яғни оның механикалық әрекетін байқауға болады.
Бірақ кез келген дене жарықты азды-көпті жұтады, оны дененің қызуынан байқауға болады. [2]
Дененің жарықты жұтқанда жылуы есебінен жарық энергиясын анықтау және өлшеу кең таралған және оңай орындалатын тәсіл болып табылады. Мұндай процесске дененің күн сәулесі есебінен жылуы жатады.
Жекелеген фотондардың энергиясы әр түрлі болғанымен, олардың вакуумдегі қозғалыс жылдамдығы бірдей. Фотондар жылдамдығы жарықтың таралу жылдамдығы болып табылады. Бұл жылдамдық аса үлкен. Тәжірибе арқылы ол вакуумде 300 000 кмс-қа тең екені анықталды (соңғы тәжірибелер нәтижелері бойынша ол 299 792,0 +-0,4 кмс). Мұндай жылдамдықпен бірде-бір дене, бірде-бір заттың бөлшектері қозғала алмайды.
Вакуумдегі жарық жылдамдығы -табиғаттағы мүмкін болатын ең үлкен жылдамдық.
с=300 000 кмс =300 000 000мс=3∙10^8 мс.

Бұл тұжырым табиғат заңы болып саналады.
Заттарда жарық жылдамдығы вакуумге қарағанда аз, мысалы, ауада жарық жылдамдығы -299 711 кмс, суда -225 000 кмс, шыныда -200 000 кмс.

1.13-сурет. Жарық шығаратын денелер
Жарық көздері -жарық шығаратын денелер (1.13-сурет). Олардың барлығын екі топқа бөлуге болады: дербес жарық көздері және шағылған жарық көздері.
Дербес жарық көздері өз кезегінде жылулық, люминесценциялық және плазмалық болып үш топқа бөлінеді.
Әлемдік кеңістіктегі жарықты да, жылуды да өздері шығаратын денелерге Күн мен жұлдыздарды жатқызуға болады.
Жердегі жағдайларда дербес жарық көздеріне жанып жатқан кез келген отын, электр шамының қызған қылы, кен пешінен алынған металл кесегі, найзағай жатады.
Жарықтың люминесценциялық көздеріне люминесценттік шамдар, теледидар экраны, тамырдың шірінділері, жарық қоңыздары, судың терең қабатында жүзетін балықтар, металдардың әр түрлі тұздары, радиоактивті заттар жатады. Люминесценция көзіне механикалық соққыны да жатқызуға болады, мысалы, қараңғыда қантты ұнтақтағанда, күкіртті мырыш ұнтағын екі шыны пластинаның арасына салып үйкегенде сәуле шығатынын көруге болады.
Плазмалық жарық көздеріне өздері арқылы электр тогын өткізетін газдар жатады, мәселен, жарнамалық түтікшелер, кварп шамдары, лазерлер, солтүстік шұғыла.
Көптеген денелер басқа жарық көздерінен өздеріне түсетін жарықты шағылдырып, шағылған жарық көздері қызметін атқарады: аспан күмбезі, мұхит, теңіз, көл, өзен суларының беті, өсімдік, қар, бұлт жамылғыларының беті.
Планеталар, олардың серіктері, Жердің жасанды серіктері, Ай және кометалар, метеориттер де күннің шағылған жарық көздері болып табылады.[2]

1.3 Жарықтың таралуы, шағылуы
Егер көз бен жарық көзінің арасына мөлдір емес экран (нәрсе) орналастырса, онда жарық көзі көрінбейтін болады. Бұл біртекті ортада жарық сызық бойымен -түзу түзусызықты тарайтынымен түсіндіріледі. Жарықтың таралу заңы дегеніміз -осы.
Жарықтың түзу сызықты таралуы-қадалардың көмегімен орман жолын, теміржол тораптарын, автокөлік жолдарын, аэродромдағы ұшу жолдарын түзу етіп төсеуге мүмкіндік береді. Бұл құбылысты теңіз бен ауада арақашықтықты өлшегенде, өлшеуіш және сызбалық сызғыштың, тақталардың, жұқа тақтайшалардың жиегінің түзулігін тексергенде қолданады (1.14- сурет).

1.14- сурет. Сызбалық сызғыш

Жарық көзінен келген жарық энергиясы бойымен тарайтын сызық жарық сәулесі деп аталады.
Берілген әрі шектелген бағытта тарайтын жарық сәулелерінің жиынтығы жарық шоқтары деп аталады. Сендерге жарық шоқтары қалта фонарынан, кино көрсететін киноаппарат прожекторынан (1.15-сурет), маяк прожекторынан (1.16-сурет) белгілі.
1.15- сурет. Киноаппарат 1.16- сурет. Маяк прожекторы
прожекторы

Кез келген жарық көзінің өлшемдері болады. Егер бұл өлшемдер жарық көзінен бақылаушыға дейінгі арақашықтықпен салыстырғанда өте аз болса, онда жарық көзінің өлшемдерін елемеуге болады. Мұндай көзді нүктелік жарық көзі деп атайды. Көптеген жұлдыздардың өлшемдері Күннен үлкен болса да, олар нүктелік жарық көздерінің көрнекі мысалдары бола алады.
S көзінен тарайтын жарық шоғын конус түрінде немесе аздап шашырайтын параллель сәулелер түрінде кескіндеуге болады.
Егер бірнеше жарық шоқтары әр түрлі көздерден таралып, бір-бірімен өзара қиылысса, онда олар бір-біріне ешқандай әсер етпейді. Бұл жарықтың жарық сәулелерінің немесе шоқтарының тәуелсіздігі деп аталатын қасиеті бар екенін білдіреді.
"Жарық сәулесі", "жарық шоғы", "нүктелік жарық көзі" ұғымдары табиғатта және тәжірибелерде бақыланатын жарық құбылыстарын сызбаларда график түрінде кескіндеу үшін қолданылады.

1.17- сурет Көлеңке
Көлеңкенің пайда болуы жарықтың біртекті ортада түзусызықты таралуымен түсіндіріледі. Жарық көзінен жарық түспейтін мөлдір емес нәрсенің сыртындағы кеңістіктің бөлігін көлеңке деп атайды.
Ашық күндері адамдардың, үйлердің, ағаштардың және басқа нәрселердің көлеңкелері анық көрінеді. Бұл құбылыстарды толығырақ қарастырайық. Ол үшін кішкене S жарық көзін, мысалы, қалта фонарының шамын алайық. Одан ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.